Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium

Shafiq Ahmad,S.Nadeem, and Noor Muhammad

Department of Mathematics, Quaid-I-Azam University 45320, Islamabad 44000, Pakistan

(Received August 28, 2018; revised manuscript received September 9, 2018)

Abstract This research is made to visualize the boundary layer flow by a curved stretching sheet embedded in porous medium.The geometry is bended (curved), therefore the curvilinear coordinates are used to model the present problem.Fluid is electrically conducting with the presence of uniform magnetic field.The governing non-linear partial differential equation reduces to non-linear ordinary differential equations by using the dimensionless suitable transformations.The numerical solutions are obtained by using the method bvp4c from MATLAB.The effects of curvature parameter, nondimensional magnetic parameter, and porosity parameter on the velocity field and skin friction coefficient are examined.The skin friction profile enhances with enhancing the values of porosity and magnetic parameter.Comparison of the present results with the existing results in the literature for the flat surface is also given.

Key words: viscous fluid,porous medium,curved stretching sheet,numerical solution,magnetohydrodynamic(MHD)

Nomenclature

1 Introduction

The viscous boundary layer flow caused by a stretching sheet moving with a certain velocity often occurs in many industrial and engineering processes.These flows have extensive applications in industries, for example in the drawing of plastic films or in the extrusion of polymer sheet from a die.During the production of the respective sheets, the melt issues from a slit are accordingly stretched to get the required thickness.The mechanical characteristic of the subsequent product depends on the cooling and stretching rates in the process.Crane[1]proposed the steady two-dimensional flow of a viscous fluid past a stretching surface.An exact closed-form solution was obtained for Crane’s problem in fluid dynamics.Further, the work of Crane was extended in several ways to add other physical features like blowing or suction,magnetic field,and heat transport phenomenon,etc.Mehmoodet al.[2]incorporated the heat transport phenomena in a flow of Jeffrey nanofluid past a stretched plate.Muhammadet al.[3]investigated the heat transfer phenomenon in the presence of thermal stratification of ferrofluid over a stretching surface.Muhammadet al.[4]utilized the Cattaneo-Christov heat flux model to discuss the squeezed flow in nanofluid over a stretching sheet.Zeeshanet al.[5]demonstrated the heat transfer in the flow of ferrofluid via stretching surface.Maqboolet al.[6]used a stretching surface to explore the Falkner-Skan boundary layer flow.

In fluid mechanics, porous medium is a substance containing voids (pores).The voids are filled usually with a fluid.The skeletal portion of the substance is called frame.The frame is typically solid, but structures like foams are analyzed using the concept of porous media.The porous medium is incorporated by its porosity.Porous medium has also the properties of permeability, electrical conducting, tortuosity, and tensile strength.The deviation of these properties of porous medium is complex due to the pores structure and media porosity.Certain natural materials and substances including rocks and soil (e.g.petroleum resources, aquifers), biological tissues (e.g.wood, bones, cork), zeolites and several other man made substances like cements and ceramics can be considered as porous media.In this direction, lots of work exists in the literature.Sheikholeslamiet al.[7]scrutinized the heat transfer flow past a permeable stretching wall embedded in porous medium.The Numerical study of nanofluid transportation in porous media with external magnetic source is established by Sheikholeslami and Ganji.[8]Nadeem and Muhammad[9]indicated the flow dripping with porous medium using Cattaneo-Christov heat flux model.Debasish[10]symbolized the non-Newtonian effect on hydromagnetic stratified dusty fluid flow along a porous media.Devakaret al.[11]examined fully developed flow in a straight uniform square duct of non-Newtonian fluids saturated in a porous medium.Ellahiet al.[12]expressed the heat transfer phenomenon in a third grade fluid embedded in porous medium.Vajravelu[13]taken stretching surface to discuss heat transfer flow embedded in porous medium.

With rapid progress of modern engineering technology,the curved stretching has got extensive attention due to its various applications in transportation, industrial, and electronics.Sanniet al.[14]obtained the numerical solution of viscous fluid saturated in curved stretching sheet.In the presence of magnetic field, the viscous fluid flow over a curved sheet were established by Abbaset al.[15]Nadeemet al.[16]indicated the chemically reactive species in the flow of Maxwell fluid over a stretching channel.Hayatet al.[17]utilized the curved stretching sheet to examine the convective flow with chemical reaction.Rosca and Pop[18]explored the unsteady boundary layer flow along a permeable curved shrinking/stretching surface.Hayatet al.[19]analyzed the homogeneous-heterogeneous reaction past a curved sheet with magnetohydrodynamic.In all these articles the stretching is curved,and to the best of our knowledge there is not a single article in the existing literature regarding the stretching flow in presence of porous medium and magnetohydrodynamic past a curved surface.In this article, we present a numerical study to obtain the solution of non-linearly ordinary differential equation by using bvp4c fromMATLAB.The graphical behavior of sundry parameters is presented.Some application about stretching sheet,porous media,and magnetic field is given in Refs.[20–28].

2 Mathematical Formulation

Consider the steady two-dimensional and an incompressible viscous fluid past a curved stretching channel coiled in a circle of radiusRabout the curvilinear coordinatesrands, as shown in Fig.1, so that large value ofRcompares to a slightly curved surface.The fluid is embedded in a porous medium and the surface is stretched along thes-direction with velocityuw=cxand atr-direction the transfer magnetic field of strengthB0is applied.Under the boundary layer approximation, the governing equations for the flow problem are given as:

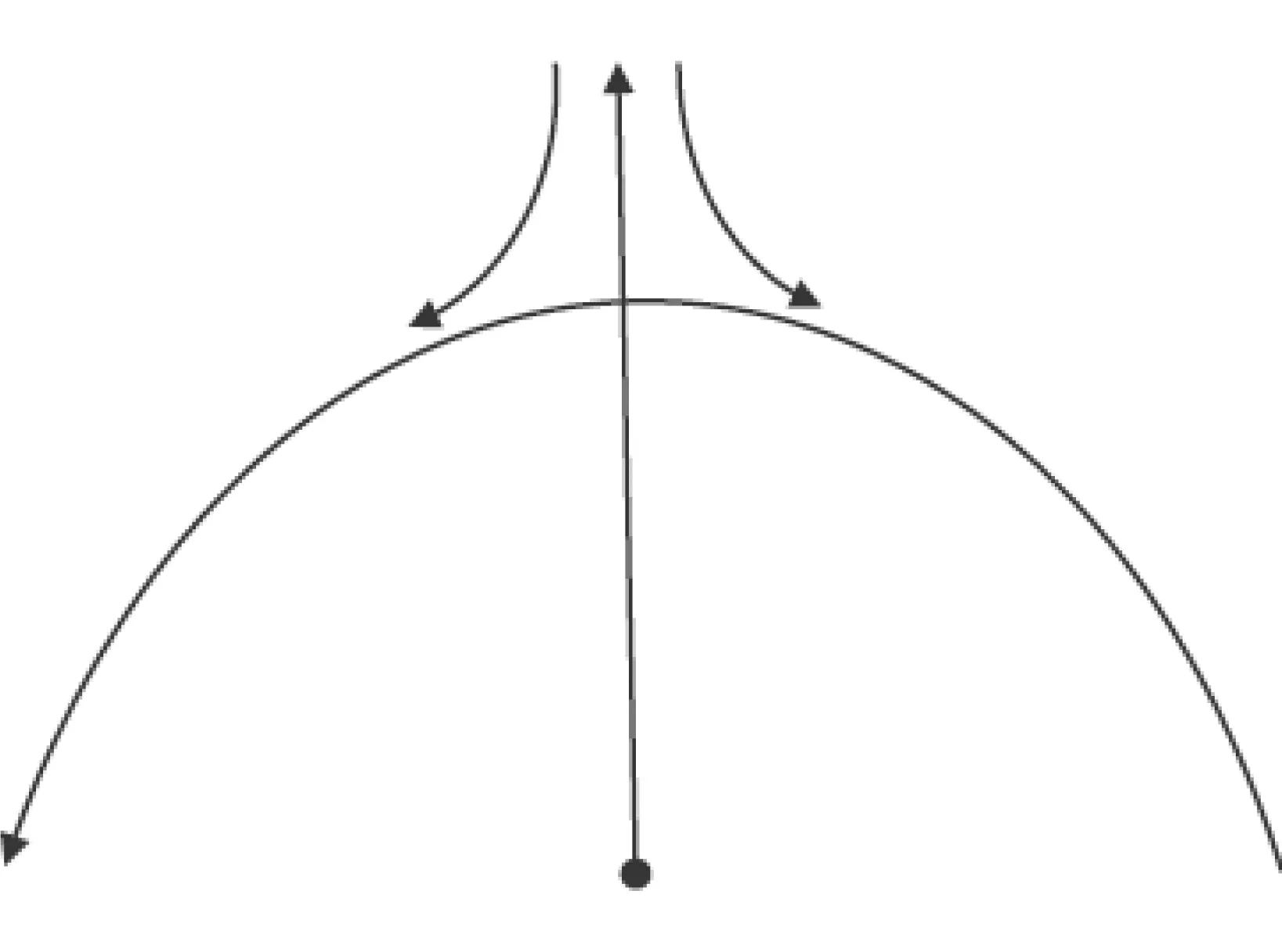
Fig.1 Geometry of the flow.

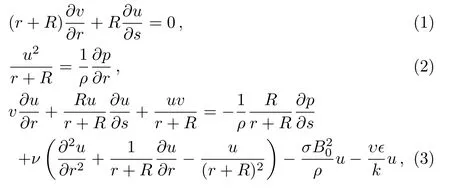
wheresandrare the curvilinear coordinates taken along the sheet and normal to it respectively,uandvare the velocity components respectively,pindicates pressure,υdemonstrates the kinematic viscosity,σexpresses the electrical conductivity of the fluid, andB0signifies the constant magnetic field.

For the velocity profile boundary conditions are

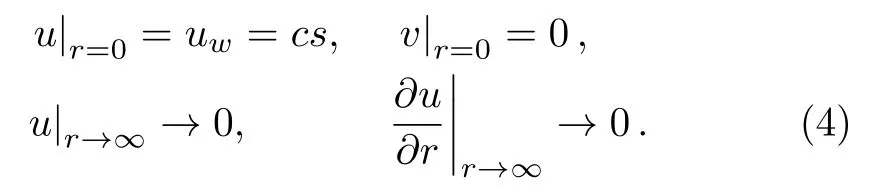
Hereuwis the stretching velocity alongs-direction andcis positive stretching constant.

3 Solution Procedure

Here we introduce the following dimensionless variables as:

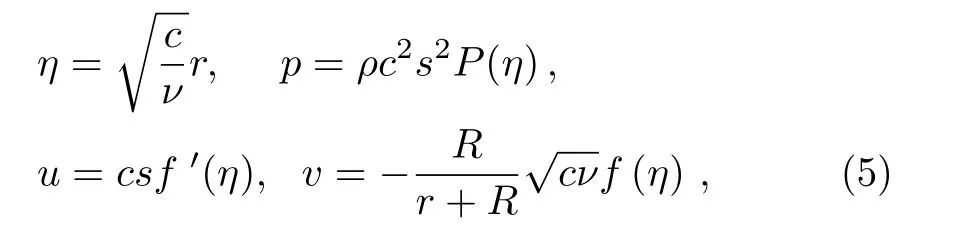
where prime denotes differentiation with respect toη.These transformations satisfy the continuity equation identically and Eqs.(2)and (3)are reduced to ordinary differential equations

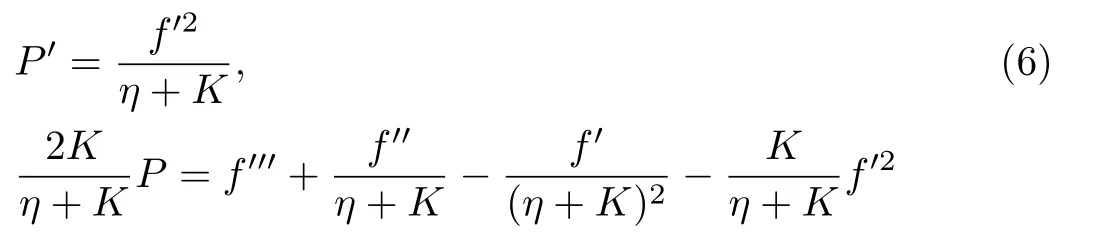
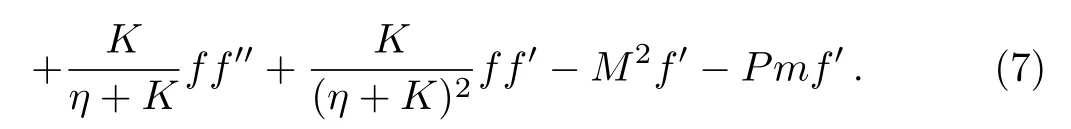
Hereindicates parameter of curvature and it should be constant,M2=σB20/ρcis the dimensionless Hartman number or magnetic parameter andPm=ν?/kcharacterizes the porosity parameter.It is worth mentioning that whenK →∞,Pm= 0, and in the absence of body forces and pressure gradient Eq.(7)reduces to classical problem of flat stretching surface studied by Crane.[1]

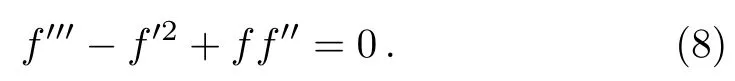
Now eliminating pressure between Eqs.(6)and (7)first we differentiate Eq.(7)with respect toηand then put Eq.(6), we get finally

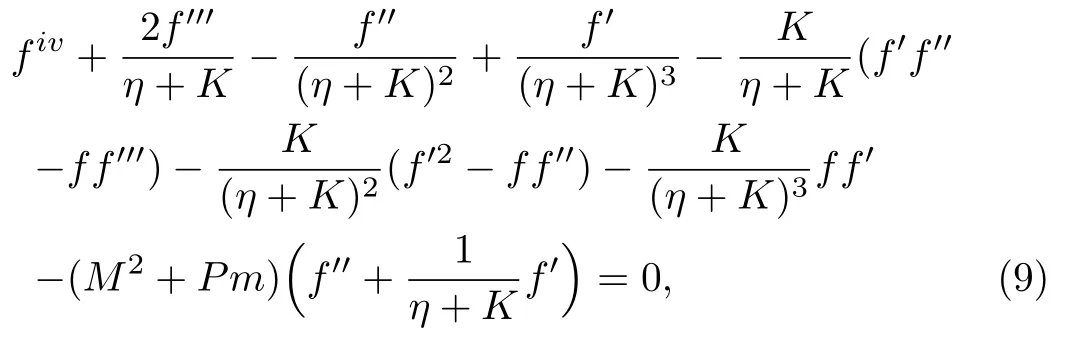
which the boundary conditions are

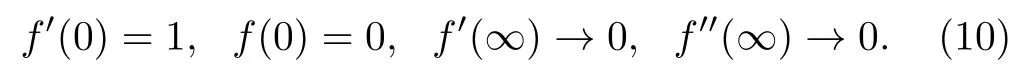
The pressure can be obtained from Eq.(7)of the form

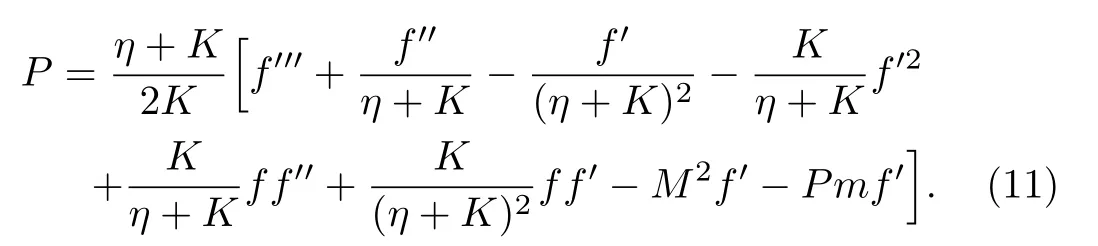
Now the surface drag forceCfins-direction is defined as

In above equationτrssimplifies the wall shear stress beside thes-direction can be given as

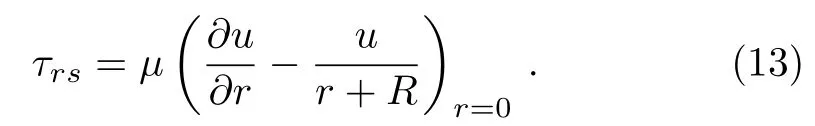
Using transformation Eqs.(5)and(14), Eq.(13)becomes

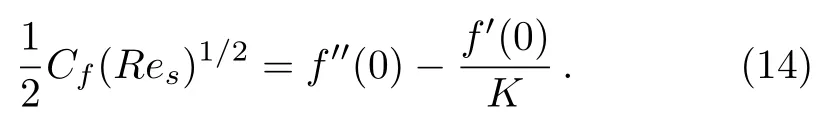
HereRes=cs2/νdemonstrates the local Reynold number.

4 Results and Discussion

The numerical method bvp4c fromMATLABis utilized to solve the numerical solution for the non-linear ordinary differential Eq.(9)with boundary condition(10)for several values of magnetic parameterM, porosity parameterPm, and dimensionless curvature parameterK.For this method first we transformed the fourth order differential equation to system of the first order differential equation by introducing new variables.The tolerance for the present problem is taken as 10?7and the function bvp4c requires an initial guess for the solution.The guess we chose must fulfill the boundary condition(10)and keep the behavior of the solution.Table 1 signifies the comparison of skin friction coefficient?CfRe1/2swhenM= 0 andPm= 0 with those of Abbaset al.[15]and Table 2 shows the numerical solution for skin friction coefficient with different values ofM,PmandK.

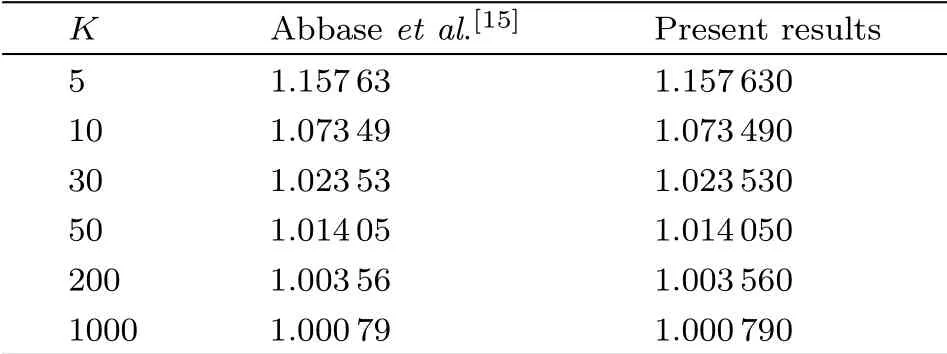
Table 1 The comparison of Skin friction with previous result Abbase et al.[15]

Table 2 The value of skin friction for different values of parameters.

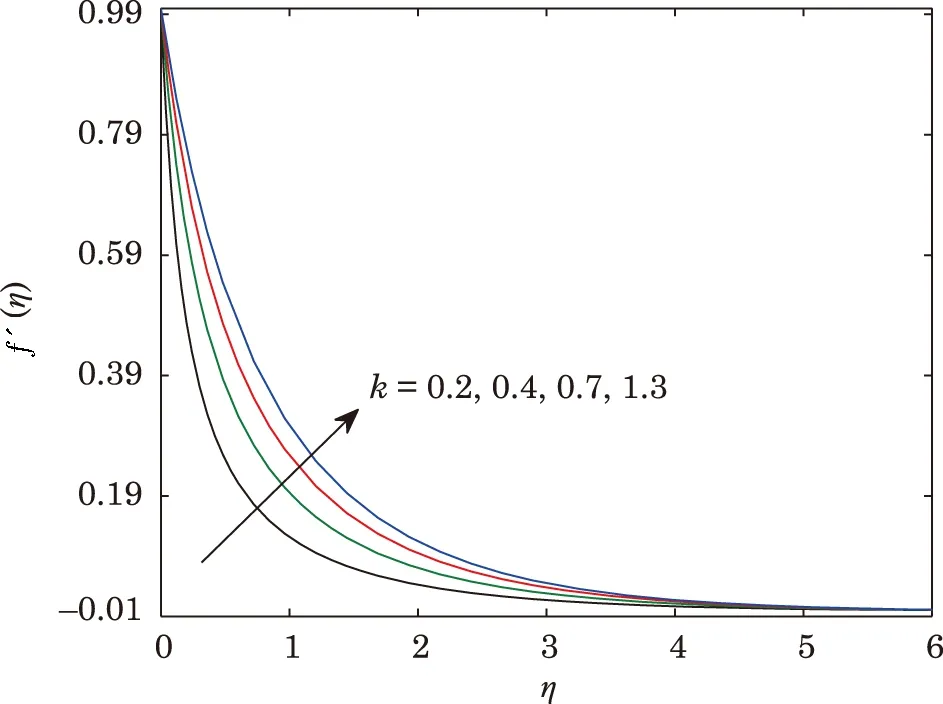
Fig.2 Effect of K on f′(η).

Figure 2 illustrates the influence of curvature parameterKwithM=0.3 andPm=0.5 is fixed,on the velocity profile.It can be seen that for rising values ofK,result in the enhancement of fluid velocity.This is because the radius of the surface increases with enlarging the value of curvature parameterK,which demonstrates the increment of fluid velocity.The boundary layer thickness also increases for larger values ofK.Figure 3 elucidates the change in the velocity profilef ′(η)for various estimation of magnetic parameterMwithK=0.1 andPm=0.5 are fixed.Here enhancement inM, leads to decay the magnitude of fluid velocity.It is due to fact that the resistive force (so-called Lorentz force)produced by magnetic field that is why the fluid velocity decreases.Figure 4 displays the characteristic of dimensionless porosity parameterPmon fluid velocity field.

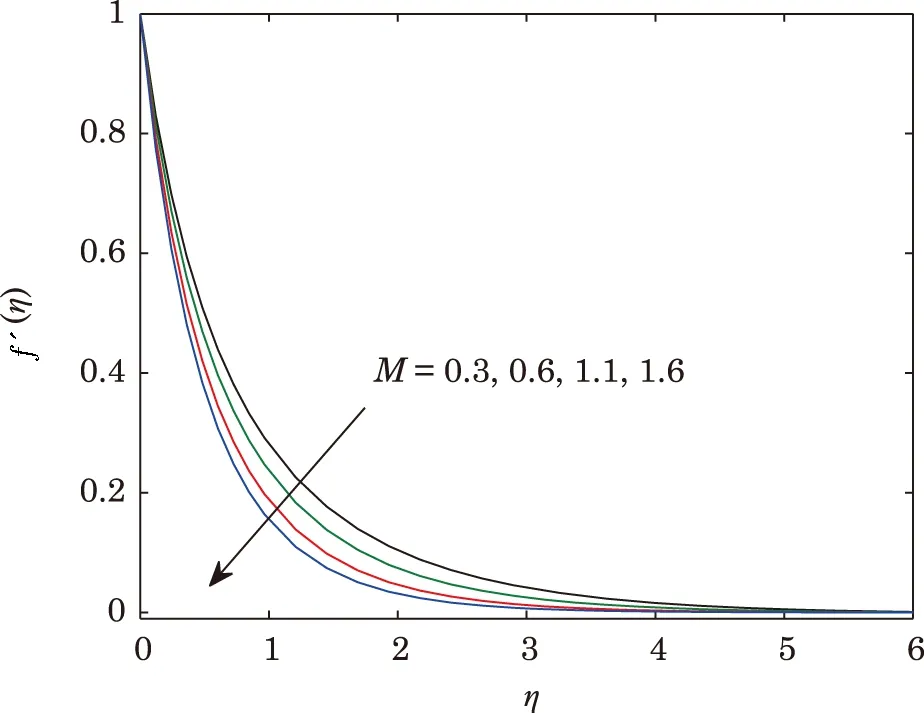
Fig.3 Effect of M on f′(η).

Fig.4 Effect of Pm on f′(η).

It is found that the fluid velocity has inverse relation with porosity parameter,i.e.for enlarging values of porosity parameter the fluid velocity becomes thinner.In fact porous medium presence increases the resistance to fluid motion, which produces reduction in fluid velocity and related momentum layer thickness.The values assign to remaining parameters areK=0.1 andM=0.3.

The mathematical expression for skin friction coefficient is given in Eq.(14).The effect of parametersKon skin friction coefficient?CfRe1/2svia magnetic parameterMandPm= 0.5 are fixed is indicated in Fig.5.It is observed that the surface drag force decreases with enlarging the value of curvature parameterK.From Fig.5 one can see that the absolute value of the skin friction increases by increasing the value ofM, however it is decreasing by increasing the curvature parameterK.While in Fig.6 the impact of porosity parameterPmversesMon skin friction coefficient is demonstrated and it is found that the surface drag force increases with increment in porosity parameterPmandK=10 are fixed.

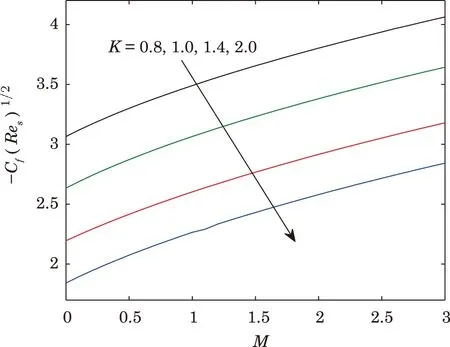
Fig.5 Effect of K on wall shear stress.

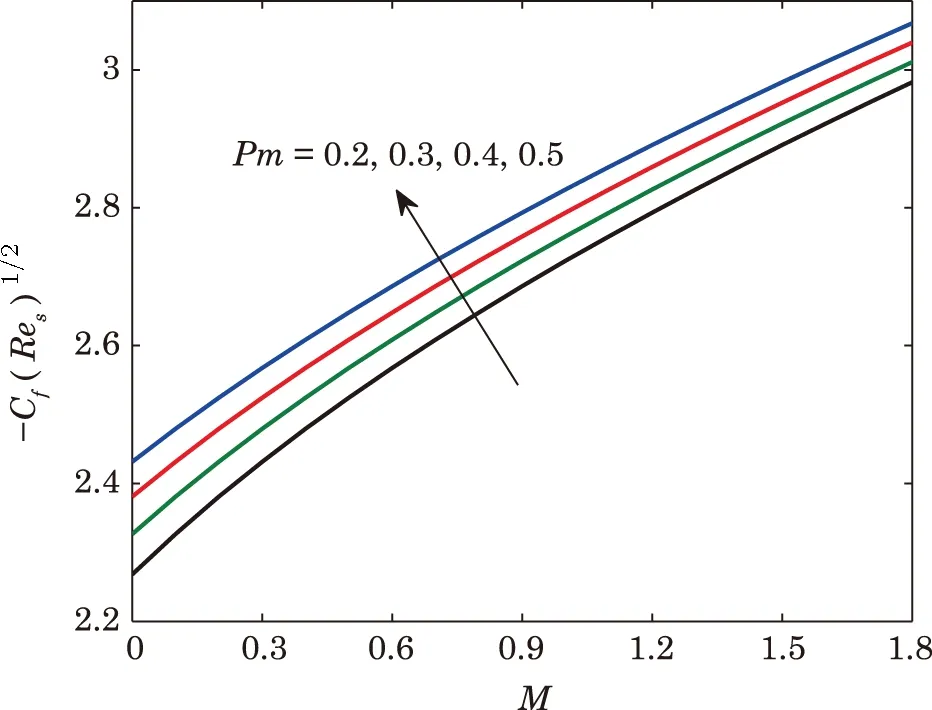
Fig.6 Effect of Pm on wall shear stress.

5 Concluding Remarks

The property of the magnetic field in a viscous fluid over a steady curved stretching surface embedded in the porous medium is investigated.The following conclusion is made.

(i)Velocity profile and boundary layer thinning rises for enlarging values of curvature parameterK.

(ii)Fluid velocity has opposite behavior for larger values ofM.

(iii)Opposite behavior of porosity parameterPmare seen on the velocity.

(iv)For increasing the value ofKandMthe surface drag force decreases.

(v)The magnitude of skin friction coefficient?CfRe1/2sincreases with larger the value ofPm.