基于FOA-GRNN模型的轉爐煉鋼終點預報

，， ，

(東北大學冶金學院，沈陽110819)

隨著“中國制造2025”的提出，數(shù)字化和智能化生產(chǎn)已成為鋼鐵工業(yè)搶占產(chǎn)業(yè)發(fā)展制高點的關鍵.作為當前世界上最主要的煉鋼技術，轉爐煉鋼在傳統(tǒng)的“高爐—轉爐”生產(chǎn)流程中扮演著重要的角色.轉爐利用氧氣與鐵水中各種元素的反應，來控制鋼液成分與溫度，其程度對鋼液質(zhì)量及后續(xù)生產(chǎn)均會產(chǎn)生重要影響.然而，由于眾多復雜的物理化學反應帶來了大量無法引入模型的影響因素，導致利用傳統(tǒng)數(shù)學模型對該過程進行描述時，往往存在適應性差、誤差較大等問題，難以滿足實際生產(chǎn)要求[1].因此，建立更加準確、高效的轉爐終點預報模型對于現(xiàn)場實際生產(chǎn)及工藝優(yōu)化均具有重要的指導意義.

近年來，神經(jīng)網(wǎng)絡技術逐漸興起，因其具有自主學習、聯(lián)想儲存和高速尋找最優(yōu)解等優(yōu)點，可學習和自適應不確定的系統(tǒng)并充分逼近任意復雜的非線性關系，并有效提高模型精度[2-5].本世紀初，許多學者采用常見的BP神經(jīng)網(wǎng)絡對轉爐終點進行預報并取得較好的效果[6-8].但BP神經(jīng)網(wǎng)絡具有不易收斂與易陷入局部極值點等缺陷，因此RBF神經(jīng)網(wǎng)絡逐漸興起并用于轉爐終點成分的預報[9-10].盡管RBF神經(jīng)網(wǎng)絡相比BP神經(jīng)網(wǎng)絡具有易收斂的特點，但RBF的網(wǎng)絡性能取決于神經(jīng)元與擴展速度的選取，而廣義回歸神經(jīng)網(wǎng)絡(GRNN)作為RBF神經(jīng)網(wǎng)絡的特例，不僅具有RBF神經(jīng)網(wǎng)絡的優(yōu)點，并且網(wǎng)絡穩(wěn)定性優(yōu)于RBF神經(jīng)網(wǎng)絡[11-12].因此，GRNN廣泛用于城市供水、建筑、通訊,軋鋼、礦山與醫(yī)療[12-17]等領域，并取得了較好的效果.

本文結合國內(nèi)某鋼廠轉爐車間實際生產(chǎn)數(shù)據(jù)，以非線性回歸理論為基礎建立了GRNN并對轉爐終點溫度與碳質(zhì)量分數(shù)進行預報，同時采用果蠅算法(FOA)對GRNN進行優(yōu)化，所得結果可為轉爐實際生產(chǎn)與工藝改進提供重要的參考.

1 GRNN神經(jīng)網(wǎng)絡預報模型的構建

1.1 GRNN神經(jīng)網(wǎng)絡的建立

GRNN與RBF神經(jīng)網(wǎng)絡非常相似，區(qū)別就在于多了一層加和層，并去掉了隱含層與輸出層的權值連接.GRNN結構分為輸入層、模式層、加和層與輸出層，如圖1與圖2所示.與其他前饋型神經(jīng)網(wǎng)絡不同的是：GRNN網(wǎng)絡權重是由訓練樣本確定的，不用初始網(wǎng)絡鏈接權重值、學習過程與回想過程無關、不必通過輸出值與訓練樣本的目標值差距來修正網(wǎng)絡鏈接權重值、無需迭代訓練、學習過程在于尋找最佳寬度系數(shù)(亦即Spread參數(shù)值)及網(wǎng)絡的神經(jīng)元數(shù)與訓練樣本有關.

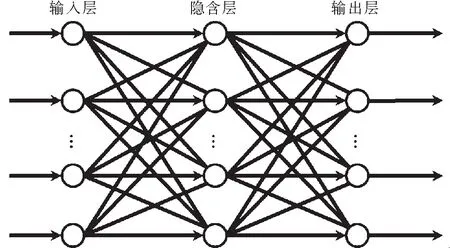
圖1 RBF神經(jīng)網(wǎng)絡結構示意圖Fig.1 Schematic of RBF neural network

GRNN是建立在非線性基礎上，根據(jù)訓練樣本提供的數(shù)據(jù)逼近其隱含的映射關系，并以最大概率準則計算網(wǎng)絡輸出.設輸入樣本為x，輸出樣本為y，x、y的聯(lián)合概率密度為f(x，y)，當x取x0時，y的期望為

借助Parzen非參數(shù)估計，按照下式估算概率密度函數(shù)f(x0,y)：

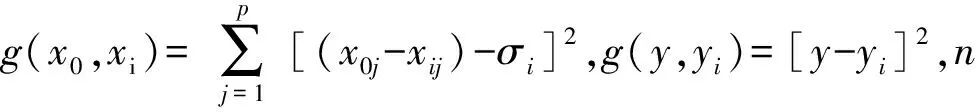
1.2 果蠅算法的引入

果蠅算法通過模擬果蠅個體的競爭與協(xié)作的行為，進而達成在空間內(nèi)尋找復雜函數(shù)全局最優(yōu)解的目的[18].果蠅算法具有易于理解、計算過程簡單、收斂速度快及易于轉化為程序代碼等優(yōu)點，因此受到工程領域的廣泛關注.

建立GRNN網(wǎng)絡的過程中，確定輸入?yún)⒘颗c輸出參量后，網(wǎng)絡性能僅取決于寬度系數(shù)的大小.寬度系數(shù)越大，網(wǎng)絡對樣本數(shù)據(jù)的逼近過程就越平緩，但逼近誤差比較大；寬度系數(shù)越小，網(wǎng)絡對樣本的逼近性能就越好，但逼近過程就越不平緩，還有可能出現(xiàn)過擬合現(xiàn)象.由于生產(chǎn)過程中的測量均存在不同程度的誤差，為了防止出現(xiàn)過擬合現(xiàn)象，一個合適的寬度系數(shù)十分重要.因此引入果蠅算法對GRNN網(wǎng)絡的寬度系數(shù)進行尋優(yōu).

1.3 數(shù)據(jù)預處理

本文所采用數(shù)據(jù)基于國內(nèi)某鋼廠轉爐車間全年生產(chǎn)數(shù)據(jù)，為提高神經(jīng)網(wǎng)絡模型的精度，選用Q235B的鋼種冶煉數(shù)據(jù)進行神經(jīng)網(wǎng)絡的建立.在5858組實際生產(chǎn)數(shù)據(jù)中，篩除錯誤、不完整及比較離散的數(shù)據(jù)后，獲得2100組有效數(shù)據(jù)，按照時間順序選取前2000組作為訓練數(shù)據(jù)，后100組作為驗證數(shù)據(jù)用作模型的測試.同時，將42種參數(shù)劃分為兩大類(即工藝條件與原料條件).

在模型的訓練過程中輸入?yún)?shù)的過多及輸入?yún)?shù)間相關性較低會導致預報模型的不穩(wěn)定，直接影響預報模型的準確性，因此需要將輸入?yún)?shù)進行篩選，去除非顯著性因素.本文采用多元線性回歸方法對輸入?yún)?shù)與輸出參數(shù)進行顯著性檢驗，并去除顯著性概率值大于0.1的輸入?yún)?shù)[19]，最終得出表1中所示各影響因素.其中，工藝參數(shù)中對鋼液溫度與碳質(zhì)量分數(shù)影響較大的參量有3種，包括供氧時間、冶煉周期及爐耗氧量；原料條件分為主料的成分、溫度、用量與輔料的用量.

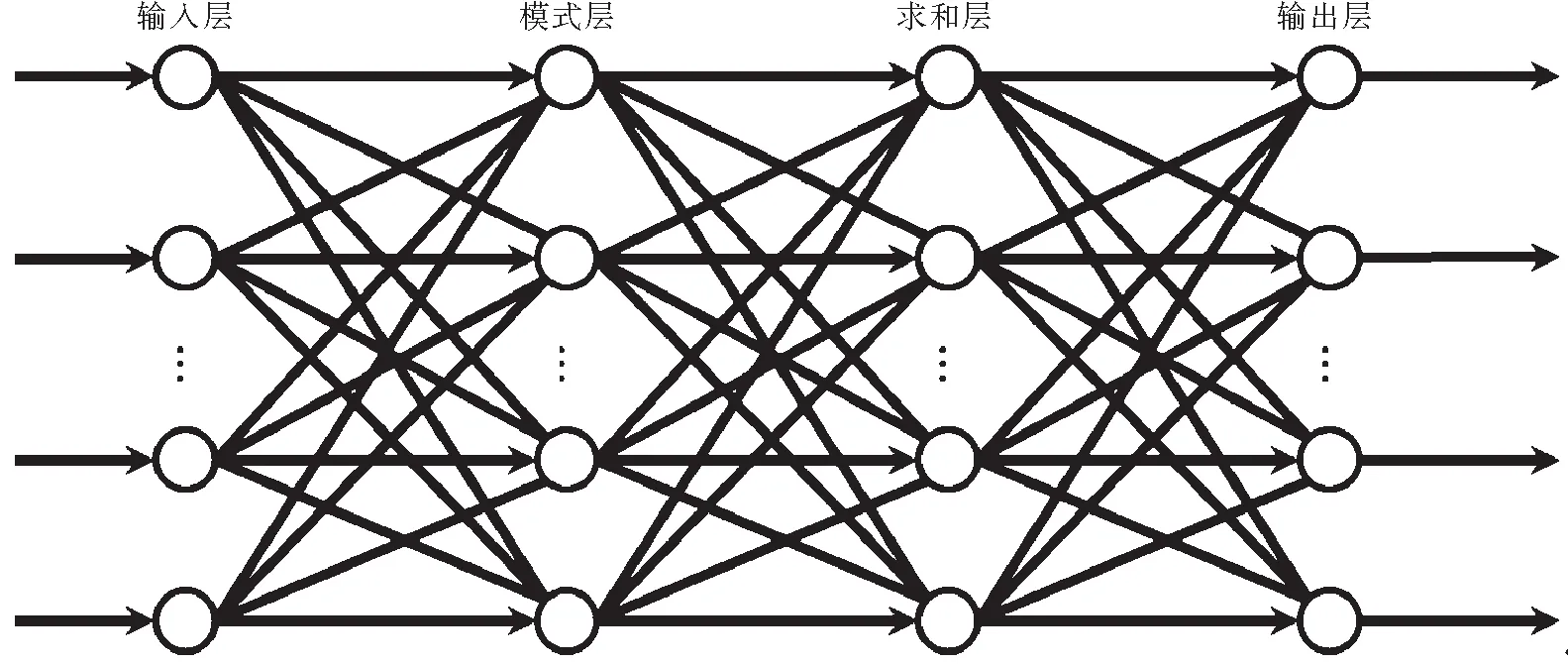
圖2 GRNN神經(jīng)網(wǎng)絡結構示意圖Fig.2 Schematic of GRNN neural network

數(shù)據(jù)類別輸入?yún)⒘枯敵鰠⒘抗に噮?shù)原料條件供氧時間海綿鐵冶煉周期w[C]iron爐耗氧量w[Si]iron鐵水溫度鐵水量石灰鋼液中碳質(zhì)量分數(shù)工藝參數(shù)供氧時間冶煉周期爐耗氧量原料條件廢鋼量w[C]iron輕燒白云石w[Si]iron鐵皮球w[Mn]iron海綿鐵w[P]iron錳礦w[S]iron硅鐵鐵水溫度鋼液溫度

實際生產(chǎn)過程中，爐耗氧量與鐵水硅含量等不僅單位不同，且相應的數(shù)值上相差可達6～7個數(shù)量級.這會導致數(shù)量級較大的數(shù)據(jù)將數(shù)量級較小的數(shù)據(jù)湮沒，影響模型收斂速度與計算精度.為此需要將數(shù)據(jù)進行標準化處理，將數(shù)據(jù)處理到[0,1]區(qū)間內(nèi)：計算公式如下所示：

(1)

式中：x0為標準化后的數(shù)據(jù)；x為初始數(shù)據(jù)；xmin為某組數(shù)據(jù)的最小值；xmax為某組數(shù)據(jù)的最大值.

1.4 預報模型的構建

基于前文所述，將果蠅算法用于優(yōu)化GRNN的寬度系數(shù).果蠅算法共有四個參數(shù)，包括初始值(X,Y)、迭代步長Length、種群規(guī)模Sizepop及迭代次數(shù)Maxgen.圖3為果蠅算法迭代尋優(yōu)流程圖，列舉了果蠅算法流程，具體步驟如圖3所示：

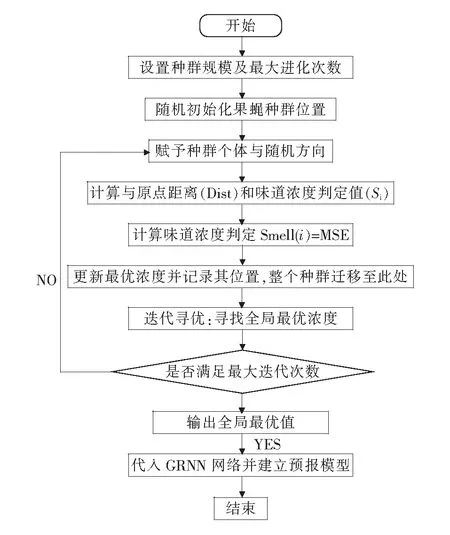
圖3 果蠅算法迭代尋優(yōu)流程圖Fig.3 Flow chart of FOA

2 轉爐終點預報結果

以FOA-GRNN模型預報轉爐終點碳質(zhì)量分數(shù)為例，采用果蠅算法對GRNN神經(jīng)網(wǎng)絡中參數(shù)進行優(yōu)化時，果蠅群體初始位置隨機初始化，果蠅群體數(shù)量為30個，迭代次數(shù)為100次，迭代搜尋方向為[-1，+1].果蠅針對寬度系數(shù)優(yōu)化路線如圖4所示，果蠅群體由初始點逐漸平穩(wěn)飛行至(1.60091,1.02881)這一坐標使結果收斂并保持穩(wěn)定.如圖5果蠅算法迭代結果所示，果蠅算法迭代至第33步時，均方差收斂至0.04707并保持穩(wěn)定直至迭代結束.

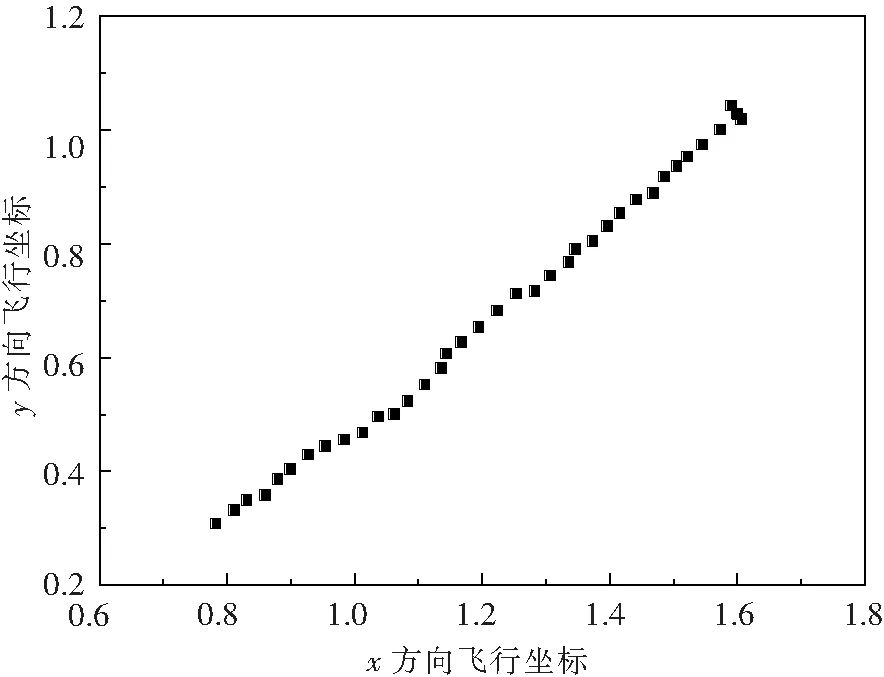
圖4 果蠅算法迭代飛行路徑 Fig.4 Flying route of fruit fly in FOA

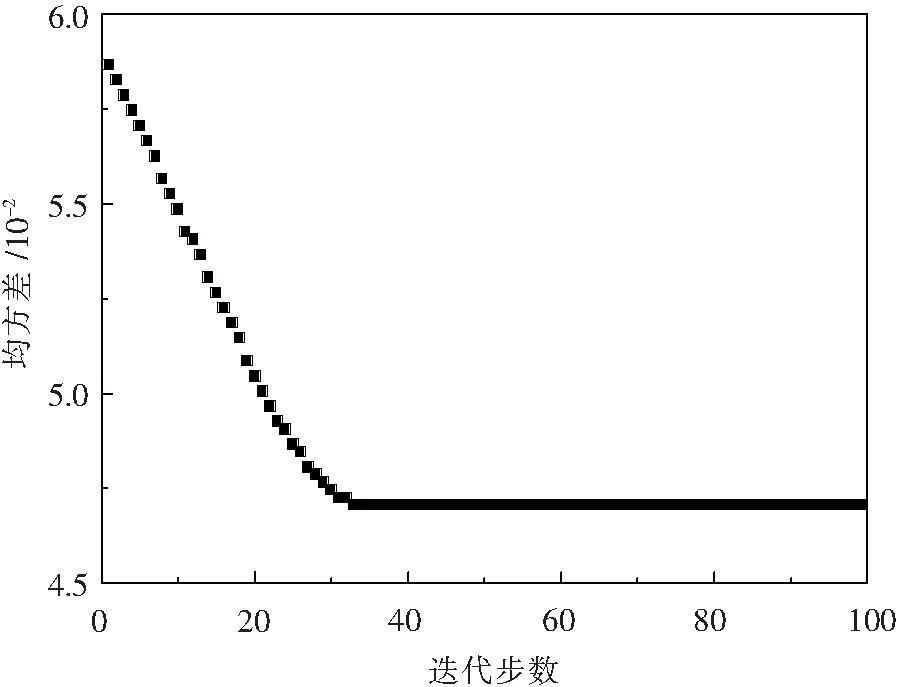
圖5 迭代結果 Fig.5 Iteration Results

圖6為RBF與FOA-GRNN神經(jīng)網(wǎng)絡預報模型對轉爐終點溫度與碳質(zhì)量分數(shù)預報結果與實際結果對比圖.由圖中可以看出RBF與FOA-GRNN神經(jīng)網(wǎng)絡預報模型預報值與實測值相差較小，兩模型溫度與碳質(zhì)量分數(shù)預報值的偏差分別集中在±15℃與±0.03%范圍內(nèi).由此可見RBF與GRNN神經(jīng)網(wǎng)絡預報模型對轉爐終點溫度與碳質(zhì)量分數(shù)均具有較高的預報精度.由圖6(a)與(b)可見，相比于RBF，GRNN對終點溫度的預報值較高，同時，在誤差為±15℃內(nèi)的FOA-GRNN模型的命中率高于RBF模型.由圖6(c)與(d)可見，兩種模型對轉爐終點碳質(zhì)量分數(shù)進行預報結果有較大的差異.與RBF模型相比，F(xiàn)OA-GRNN模型的預報值較為集中，使FOA-GRNN模型在誤差為±0.03%時的命中率高于RBF模型.

圖7為RBF與FOA-GRNN神經(jīng)網(wǎng)絡預報模型預報誤差分布圖.由圖7(a)中可見，RBF模型對碳質(zhì)量分數(shù)預報誤差為±0.04%時，共有99組數(shù)據(jù)在此區(qū)間內(nèi)，命中率達到99%；當預報誤差在±0.03%范圍內(nèi)時模型命中率為91%.RBF神經(jīng)網(wǎng)絡預報模型的預報精度雖可滿足生產(chǎn)要求，但仍有改進的空間.采用FOA-GRNN模型對碳質(zhì)量分數(shù)預報誤差在±0.04%區(qū)間內(nèi)的數(shù)據(jù)為99組，命中率達到99%；誤差分布在±0.03%區(qū)間內(nèi)的數(shù)據(jù)為94組，命中率達到94%.由圖7(b)可見，F(xiàn)OA-GRNN模型對轉爐終點溫度的預報結果優(yōu)于RBF神經(jīng)網(wǎng)絡預報模型.RBF與FOA-GRNN神經(jīng)網(wǎng)絡預報模型對溫度的預報誤差分布在±15℃區(qū)間內(nèi)的數(shù)據(jù)分別為89組與97組，命中率分別為89%與97%；預報誤差分布在±20℃區(qū)間內(nèi)的數(shù)據(jù)分別為95組與99組，命中率分別為95%與99%.

由此可見，與RBF模型相比，F(xiàn)OA-GRNN模型對轉爐終點溫度與碳質(zhì)量分數(shù)預報的精度均具有優(yōu)勢.轉爐終點溫度與碳質(zhì)量分數(shù)預報模型準確率的提升可減少補吹次數(shù)、優(yōu)化工藝流程、降低能耗及生產(chǎn)成本、提高生產(chǎn)效率與鋼液質(zhì)量.

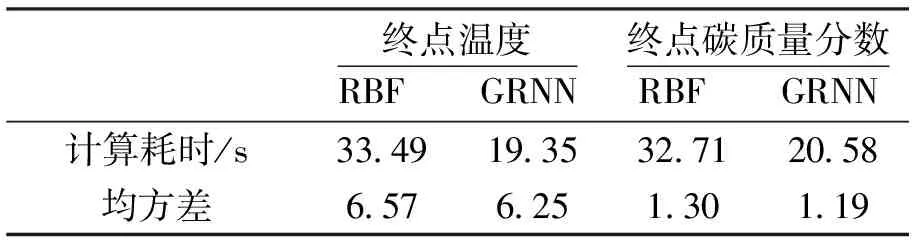
表2 兩種預報模型性能對比Table 2 Comparison of performance of the two models

為更好地比較兩種神經(jīng)網(wǎng)絡預報模型性能，引入計算耗時與均方差對預報模型的性能進行評價.表2為RBF網(wǎng)絡與FOA-GRNN網(wǎng)絡預報模型性能對比.由表中對比可以看出對終點溫度與碳質(zhì)量分數(shù)預報結果中，RBF模型計算耗時分別為33.49 s與32.71 s；FOA-GRNN模型計算耗時明顯較低，分別為19.35 s與20.58 s.由此可見，采用FOA-GRNN模型對轉爐終點溫度與碳質(zhì)量分數(shù)進行預報可以在RBF模型的基礎上減少42.22%與及37.08%的時間，顯著提高了預報效率.同時，通過對比兩模型對轉爐終點溫度與碳質(zhì)量分數(shù)的預報值與實測值的均方差可見，F(xiàn)OA-GRNN模型的均方差分別為6.25與1.19小于RBF模型的6.57與1.30.因此，與RBF網(wǎng)絡模型相比，F(xiàn)OA-GRNN模型在對轉爐終點溫度與碳質(zhì)量分數(shù)的預報過程中以較少的計算資源獲得更準確的結果，并具有方便訓練、適應性好及易于向現(xiàn)場推廣等優(yōu)點.

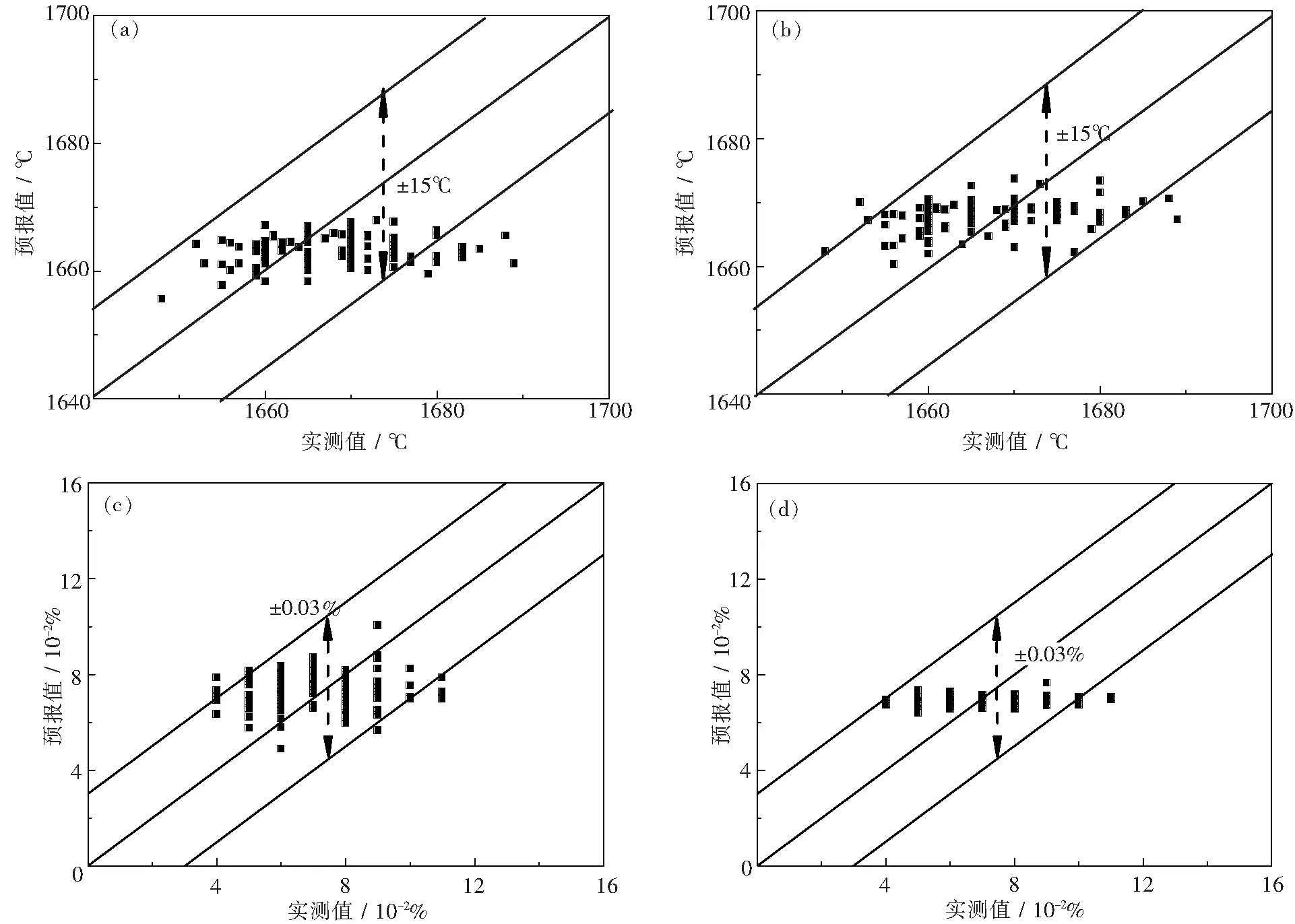
圖6 終點溫度與碳質(zhì)量分數(shù)預報結果Fig.6 Predictions of end-point temperature and carbon content(a)—RBF模型預報終點溫度；(b)—GRNN模型預報終點溫度； (c)—RBF模型預報終點碳質(zhì)量分數(shù)；(d)—GRNN模型預報終點碳質(zhì)量分數(shù)

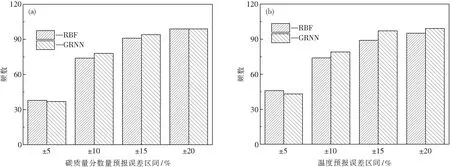
圖7 兩種預報模型結果分布對比Fig.7 Comparison of prediction results based on the two models(a)—兩種模型碳質(zhì)量分數(shù)預報誤差分布圖； (b)—兩種模型溫度預報誤差分布圖

3 結 論

本文以國內(nèi)某鋼廠轉爐車間全年實際生產(chǎn)數(shù)據(jù)為基礎，建立FOA-GRNN神經(jīng)網(wǎng)絡模型對轉爐終點溫度及碳質(zhì)量分數(shù)進行預報并與RBF神經(jīng)網(wǎng)絡預報模型結果進行對比.結果表明：

(1) FOA-GRNN神經(jīng)網(wǎng)絡報模型與RBF神經(jīng)網(wǎng)絡預報模型對轉爐終點溫度與碳質(zhì)量分數(shù)預報結果均分別集中于誤差為±15℃與±0.03%的范圍內(nèi).與RBF模型預報結果相比，F(xiàn)OA-GRNN模型預報結果在此誤差范圍內(nèi)分布更好.

(2)采用FOA-GRNN模型對碳質(zhì)量分數(shù)預報誤差為±0.03%時的命中率可以達到94%，高于RBF模型的91%；FOA-GRNN模型對終點溫度預報誤差為±15℃時的命中率可以達到97%，高于RBF模型的89%.與RBF神經(jīng)網(wǎng)絡預報模型相比，F(xiàn)OA-GRNN模型具有較高的精度.

(3) FOA-GRNN神經(jīng)網(wǎng)絡預報模型與RBF神經(jīng)網(wǎng)絡預報模型相比，可降低42.22%與37.08%的計算時間并減小預測值與實測值的均方差，因此FOA-GRNN神經(jīng)網(wǎng)絡具有計算耗時少、精度高、方便訓練及易于向現(xiàn)場推廣等優(yōu)點，可為現(xiàn)場工藝參數(shù)的制定與新鋼種的開發(fā)提供重要的參考.