考慮熱位移的電主軸系統瞬態熱特性分析

孫學

(天津工業大學 天津 300387)

電主軸與機械主軸相比，其內部結構更加復雜，不僅有軸承的摩擦發熱，內置的電機也會產生大量熱。熱量通過熱對流、熱傳導和熱輻射的方式傳遞到電主軸系統的各個部分并出現了不同的溫升，也導致了熱變形。目前對電主軸系統能夠進行的熱態性能分析大部分是在穩態溫度場的前提下，實際上，高速運轉中的電主軸系統屬于熱時變系統，其熱源生熱率、熱邊界條件等熱特性參數會隨著溫度場和熱變形的變化而時刻變化。因此，對電主軸-軸承系統進行考慮熱與變形耦合的瞬態熱特性分析，才能更準確的描述電主軸系統的熱態特性。

一、電主軸系統的熱位移

假設溫度在軸承系統各部分均勻分布，且轉軸、軸承內圈、滾動體、軸承外圈和軸承座的溫升分別為ΔTs、ΔTi、ΔTb、ΔTo和ΔTh，那么，考慮轉軸熱位移影響的滾動體內外圈溝道相對徑向熱位移ur和軸向熱位移ua的表達式為：

-αhΔTh(1+ν)Do+2αbΔTbDw

(1)

(2)

式中，Di、Do分別為軸承內外圈溝道直徑，d為轉軸外徑，Dw為滾動體直徑，ν為材料泊松比，α為材料熱傳導系數，Ls、Lh分別為轉軸與軸承座的長度。

由上述分析可得到軸承接觸線上的總相對熱位移un的表達式為

un=urcosα+uasinα

(3)

由熱位移引起的熱誘導預緊力FT的表達式為：

(4)

式中，Kn為軸承的法向接觸剛度。

二、電主軸瞬態熱傳遞模型的建立

(一)熱節點的劃分及熱網絡參數的確定

由于整個電主軸系統是中心對稱的，不需要考慮圓周方向的傳熱，因此可以將電主軸的三維傳熱過程簡化為一維的。根據電主軸的結構及各零件的材料，將電主軸系統劃分為58個熱節點，如圖1所示。圖中，“·”代表所劃分的熱節點的位置。

圖1 電主軸熱節點分布圖

將轉軸、軸承內外圈等部件均簡化為空心圓筒，根據熱阻定義及材料和尺寸，可以求得各節點間的軸向和徑向熱阻。

軸承發熱量可由文獻[3]介紹的計算方法求得，電機的發熱量可由電機手冊查得得到，計算時假定定子產生的熱量占總發熱量的2/3，轉子產生的熱量占總發熱量的1/3。

(二)瞬態熱平衡方程的建立

對于瞬態傳熱，任意時刻節點的凈熱流量等于該節點相關體積內能的增加量，那么任意時刻節點的瞬態熱流平衡方程如下：

(5)

式中，Ri-n為節點之間的熱阻，Qi為該節點發熱量，ρi節點密度，ci為節點比熱容，Vi為該節點的相關體積。

(6)

將(4-22)代入公式(4-18)，就得到了任意節點的瞬態熱平衡方程的數值解形式：

(7)

這樣公式(4-21)所示的瞬態熱平衡求解的微分方程組就離散成了以Δt為步長的線性方程組，將每一步求出來的溫度場作為下一步的輸入條件即可遞推求得下一時刻的溫度場，其計算流程圖如圖2所示。

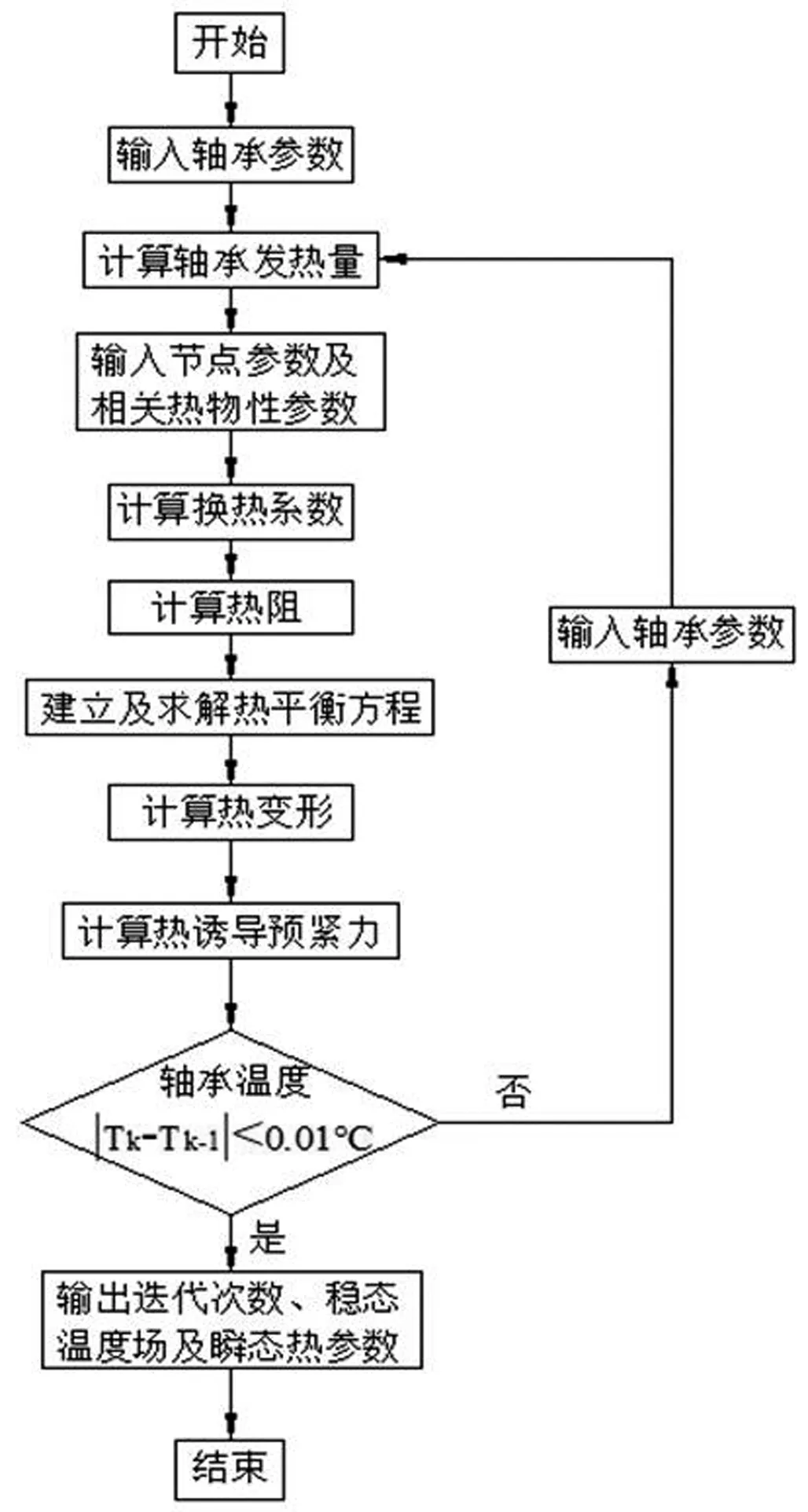
圖2 瞬態熱分析計算流程圖

三、電主軸系統瞬態熱特性分析

(一)瞬態溫升情況分析

在不同轉速和不同初始預緊力下軸承的瞬態溫升曲線如圖3所示。

(a)轉速對軸承瞬態溫升曲線的影響 (b)預緊力對軸承瞬態溫升曲線的影響

圖3轉速和預緊力對軸承1瞬態溫升曲線的影響

從圖3中可以看出，溫度在開始階段迅速上升，之后變化梯度逐漸減慢，最后達到穩定狀態。轉速越高，初始預緊力越大，電主軸的軸承的溫升也越大。同時可以看出，盡管隨著轉速和預緊力的增大，溫升越來越大，但是電主軸系統中軸承達到熱平衡的時間變化很小。

(二)軸承內外圈瞬態相對熱位移分析

在不同轉速和不同預緊力下軸承的瞬態相對熱位移變化曲線如圖4所示。

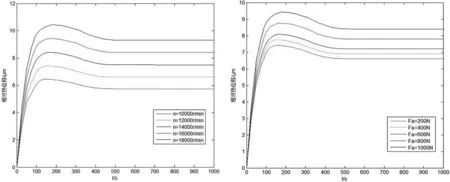
(a)轉速對瞬態相對熱位移的影響 (b)預緊力對瞬態相對熱位移的影響

圖4轉速和預緊力對軸承內外圈瞬態相對熱位移的影響

從圖4中可以看出，相對熱位移在開始階段迅速增大，之后又逐漸減小，最后趨于穩定。這是由于開始階段軸承內外圈膨脹量的不同導致了相對熱位移的迅速增加，之后軸承座逐漸膨脹放松了軸承的外圈，內外圈相對熱位移又逐漸減小，最后當系統達到熱平衡時，相對熱位移達到穩定。圖中也可以看到隨著轉速和初始預緊力的增加，軸承內外圈的相對熱位移也逐漸增大，但在不同轉速和初始預緊力的條件下相對熱位移瞬態曲線的趨勢是一致的。

(三)軸承瞬態熱誘導預緊力分析

不同轉速和初始預緊力下的軸承瞬態熱誘導預緊力的變化曲線如圖5所示。

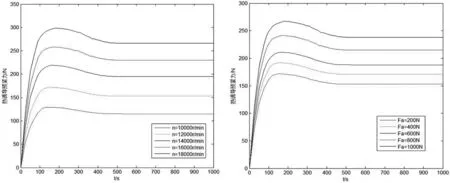
(a)轉速對瞬態熱誘導預緊力的影響 (b)預緊力對瞬態熱誘導預緊力的影響

圖5轉速和初始預緊力對軸承瞬態熱誘導預緊力的影響

從圖5中可以看出，瞬態熱誘導預緊力曲線的變化趨勢也是在開始階段增長迅速，之后又逐漸減小，最后趨于穩定。這是由于熱誘導預緊力是由相對熱位移直接引起的，它們之間的關系基本是線性的。圖中還可以看出隨著轉速和初始預緊力的增加，軸承的熱誘導預緊力也是逐漸增大。

四、結論

(1)電主軸各部分溫升都是開始階段增長迅速，之后變化梯度逐漸減小并最終趨于穩定的，且各部分達到熱平衡的時間基本一致。

(2)電主軸軸承的相對熱位移和熱誘導預緊力都是開始階段迅速增加，之后又逐漸減小，最后當電主軸達到熱平衡時軸承熱位移和熱誘導預緊力達到穩定狀態。

(3)隨著轉速和初始預緊力的提高，電主軸各部分溫升、軸承相對熱位移和熱誘導預緊力都有所增加，但不同轉速和初始預緊力下，它們的瞬態曲線變化趨勢基本是一致的。