抓住浮力習題教學的要點

霍曉宏

(天津市教育科學研究院 天津 300191)

浮力問題是初中物理教學的重點和難點，是學生最難把握的內容之一．教學中，學生往往對一些浮力現象很感興趣，但習題解答起來卻感到困難，有不少學生只能機械地套用公式或記住一些二級結論．歸其原因：一是浮力問題是在力、密度、壓強等知識學習的基礎上進行的，有一定的綜合性．二是浮力習題題型多、內容廣，學生缺少分析、歸納及靈活應用的能力，所以面對不同的“浮力習題”就顯得有些“吃力”．

要破解初中物理浮力習題教學之難，首先是要加深對基本概念和規律的理解，破除錯誤前概念的干擾，建立正確的物理觀念．然后從解題思維方法上下功夫，抓住受力分析和確定幾何關系等幾個要點．教師要引導學生盡量少記二級結論，因為許多二級結論都是有前提條件的，只記住結論而不注意條件，應用時出錯的概率會很大．要讓學生脫離題海，教師就要從題海中選擇出有意義的習題，注重過程與方法教學，引領學生不斷走向成功．

1 建立正確的物理觀念

“物理觀念”是從物理學視角形成的關于物質、運動與相互作用、能量等的基本認識，是物理概念和規律等在頭腦中的提煉與升華，是從物理學視角解釋自然現象和解決實際問題的基礎[1]．初中生所學習的浮力相關知識是以浮力概念為基點，阿基米德原理為核心，物體的浮沉條件為其表現形式的．有研究表明，浮力這一概念涉及學生典型錯誤前概念主要有：

(1)重的物體下沉，輕的物體上浮；

(2)浮的物體才受到浮力，沉的物體不受浮力；

(3)物體浸沒在水中越深的位置，所受的浮力越大或者越小[2]．

除此之外，在教學實踐中發現，學生無法對物體處于漂浮、懸浮和下沉3種狀態下所受浮力大小做出正確判斷，對物體浮沉狀態與浮力和重力之間的關系認識不全面，對受到浮力作用的物體排開液體的體積的認識上有偏差，確定幾何關系往往成為難點．

基于上述原因，教學實踐中首先要通過各種形式的實驗，讓學生動手體會浮力，增加學生的感性認識；還可以應用計算機模型建構等方法幫助學生剔除錯誤的前概念．有些錯誤觀念隱藏在學生的潛意識里，在處理問題時就會暴露出來，這就要通過不斷地實踐、獨立地練習發現和剔除這些錯誤觀念．通過練習既看到不足，也看到成績，從而不斷培養學生解決問題的信心．

正確觀念的建立是一個“反復”的過程，通過設計必要的判斷題、選擇題，深化學生對浮力本質的認識．如體積相等的實心鐵塊、木塊，完全浸沒在水中時所受的浮力一樣大；質量相等的實心鐵塊、木塊，完全浸沒在水中時所受的浮力木塊大等等．通過一題多變，在不同的物理情境中，加深對阿基米德原理，即F浮=G排=ρ液V排g的理解．

有的學生學習物理，下了很大的功夫，但仍然沒有好的效果，這往往是沒有形成正確的物理觀念造成的．對物理問題的理解不到位，思維深度淺，就形不成較高的“悟性”，問題稍一靈活，便不知所措，有時往往一開始解決問題的思路就是錯誤的，必然步入歧途．教師平時教學時要重視物理思維含量高、方法通用性強、模型典型化的基本問題的練習，通過基本題的訓練來熟悉解題的基本程序，在此基礎上拓展思維發展能力．

2 養成受力分析的良好習慣

選擇研究對象，對研究對象進行正確的受力分析是解好浮力綜合習題的前提條件．當物體靜止時，如果物體只受兩個力作用，那二力一定平衡；當物體受一條直線上的3個力甚至是4個力作用靜止時，仍可轉化為二力平衡問題．如下題.

【例1】裝有金屬球的小容器A漂浮在盛有水的圓柱形大容器B的水面上，所受的浮力為F1，如圖1所示．若把金屬球從A中拿出投入水中沉到B的底部時，小容器A所受的浮力大小為F2，池底對金屬球的支持力大小為N，那么( )

A.金屬球所受重力的大小為F1-F2

B.小容器所受重力的大小為F2

C.小容器所受浮力減小了N

D.大容器底部受水的壓力減小了N

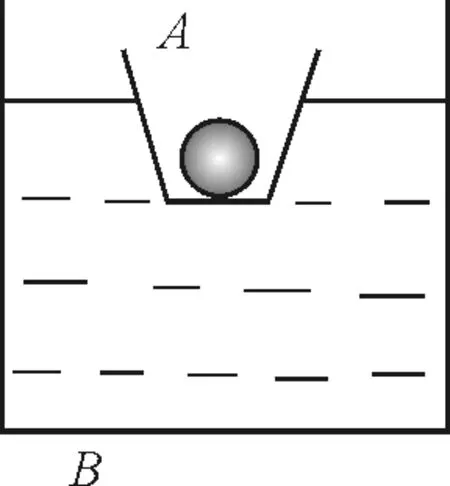
圖1 例1題圖

分析：設小容器A的重力為G，金屬球的重力為G′．以裝有金屬球的小容器A整體為研究對象，當它們漂浮在盛有水的圓柱形大容器B的水面上時，此時受到的浮力等于它們的總重力，即

F1=G+G′

(1)

把金屬球從A中拿出投入水中沉到B的底部時，小容器A處于漂浮狀態，以小容器A為研究對象，此時它受到的浮力

F2=G

(2)

由式(2)可知選項B正確.

由式(1)、(2)得

G′=F1-F2

(3)

由式(3)可知選項A正確.

以金屬球沉到B的底部時為研究對象，金屬球受重力G′、支持力N和浮力(設為F3)3個力作用而平衡，即

F3+N=G′

(4)

由式(3)、(4)可知：小容器所受浮力減小量為

F1-F2=N+F3

由此可知選項C錯誤．

以金屬球、小容器A和所有的水整體為研究對象，起初大容器底部受水的壓力大小等于整體所受的重力大小，金屬球沉到B的底部時，金屬球對池底的壓力大小為N，水對大容器底部的壓力就減小了N，故選項D正確．

此題的正確答案為選項A，B，D.

如果物體受力不平衡，物體的運動狀態就要發生改變．對于初中學生處理動態的浮力問題，可以采用假設的方法，把動態問題轉化為靜態問題來處理．如下題.

【例2】木塊漂浮在水面上，有一部分露出水面，若將露出水面的部分切掉，則( )

A.木塊下沉

B.木塊頂部與水面齊平

C.木塊懸浮在任意深度

D.木塊上浮，仍有一部分露出水面

分析：假設木塊頂部與水面齊平．切掉木塊露出水面的部分前，浮力等于木塊整體的重力．切掉木塊露出水面的部分后，剩余木塊重力變小．如果木塊頂部與水面齊平，則浮力將大于剩余木塊的重力，因此木塊將上浮，所以選項D正確．

教師平時教學要引導學生養成良好的解題習慣，做好必要的預備工作，如仔細審題、分析過程、選擇研究對象、進行受力分析，必要時畫出草圖等．有許多習題就在完成這些預備工作的過程中解決了．

3 合理確定排開液體的體積

阿基米德原理F浮=G排=ρ液V排g，即物體所受的浮力大小等于它排開的液體受到的重力．確定排開液體的體積往往與物體浸入液體的多少、物體的形狀變化、液面的升降、物態的變化等相聯系．因此，確定排開液體的體積往往成為學生解決浮力習題的難點．

3.1 根據物體進入液體的多少來確定排開液體的體積

這種方法一般應用于形狀規則、質地均勻的物體漂浮或懸浮在液體中．首先確定物體的運動狀態(如靜止)，對物體進行受力分析；然后根據物體進入液體的多少來確定排開液體的體積，即確定幾何關系；最后利用(如二力平衡)浮力等于重力，即F浮=ρ液V排g=ρVg列方程求解．如下題.

【例3】有一支蠟燭，粗細均勻，長度為20 cm，在其底端插入一個小鐵釘，使蠟燭露出水面1 cm，如圖2所示．現將蠟燭點燃，問蠟燭還剩多長時將被水淹滅？(設蠟燭油全部燃盡而不下流，ρ蠟=9×102kg/m3)

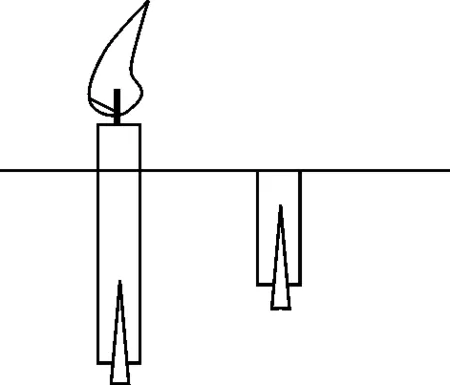
圖2 例3題圖

解析：設蠟燭總長h=20 cm=0.2 m，蠟燭未點燃時露出水面部分長度h1=1 cm=0.01 m,則此時蠟燭所受浮力

F浮1=G蠟1+G鐵

即ρ水g(h-h1)S=ρ蠟ghS+G鐵

(5)

設蠟燭被水淹滅時(即蠟燭上表面與水面相平時)蠟燭的剩余長度為h2，被水淹滅時蠟燭所受浮力

F浮2=G蠟2+G鐵

即ρ水gh2S=ρ蠟gh2S+G鐵

(6)

由式(5)、(6)整理得

h2=0.1 m=10 cm

即蠟燭還剩10 cm時將被水淹滅．

3.2 根據物體的形狀變化來確定排開液體的體積

這種方法一般應用于物體浸沒(懸浮或沉底)在液體中，物體的形狀會隨外界條件(壓強、壓力)的變化而有所變化．解題過程是：首先對物體進行受力分析，然后確定條件變化前后排開液體的體積，即確定幾何關系，利用阿基米德原理，即F浮=ρ液V排g來解決問題，如下題.

【例4】一個豎直放置、開口向下的玻璃杯全部浸沒水中，恰好處于懸浮狀態．杯內有適量的空氣，如圖3所示．如果施加外力，改變玻璃杯在水中的深度(保持玻璃杯處于豎直狀態)，然后去掉外力，下列說法正確的是( )

A．若外力使玻璃杯在水中的深度變小，去掉外力后，玻璃杯將下沉到水底

B．若外力使玻璃杯在水中的深度變小，去掉外力后，玻璃杯將回到原位置

C．若外力使玻璃杯在水中的深度增大，去掉外力后，玻璃杯將下沉到水底

D．若外力使玻璃杯在水中的深度增大，去掉外力后，玻璃杯將上浮到液面

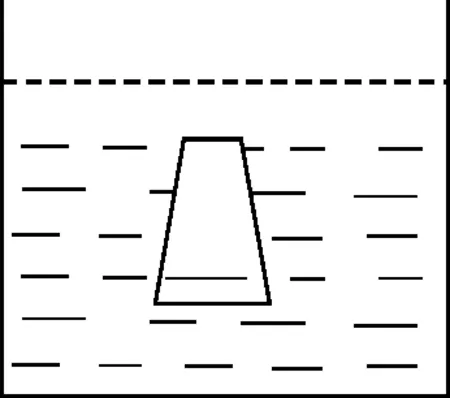
圖3 例4題圖

分析：當玻璃杯在水中的深度變小時，杯內空氣壓強減小，體積增大，排開水的體積增大，所受浮力增大．去掉外力后，玻璃杯將上浮.當玻璃杯在水中的深度增大時，杯內空氣壓強增大，體積減小，所受浮力減小．去掉外力后，玻璃杯將下沉到水底，故選項C正確．

3.3 考慮液面的升降來計算排開液體的體積

浮力稍難一些的題目很多都是浮力動態變化的過程，通過兩次或多次不同的物理情境，造成液面的升降即排開液體的體積不同．針對這種物理問題還是首先要對每種物理情境中的物體進行受力分析，然后考慮前后排開液體的幾何關系，如下題.

【例5】一塊內部含有石塊的冰塊，放在密度ρ0=0.95×103kg/m3的液體中恰好懸浮．底面積S=100 cm2的圓柱形容器中裝有水，將這塊含有石塊的冰塊放入水中后，容器中水面升高了h1=2.09 cm．冰熔化后，石塊沉入水底，水面又下降了h2=0.1 cm．求石塊的密度(g=10 N/kg)．

解析：冰塊在密度ρ0= 0.95×103kg/m3的液體中恰好懸浮應有

ρ0V冰+V石g=ρ冰V冰g+ρ石V石g

(7)

冰塊在水中漂浮，畫出草圖如圖4所示，其幾何關系由圖4(a)可見，冰塊排開水的體積為h1S．

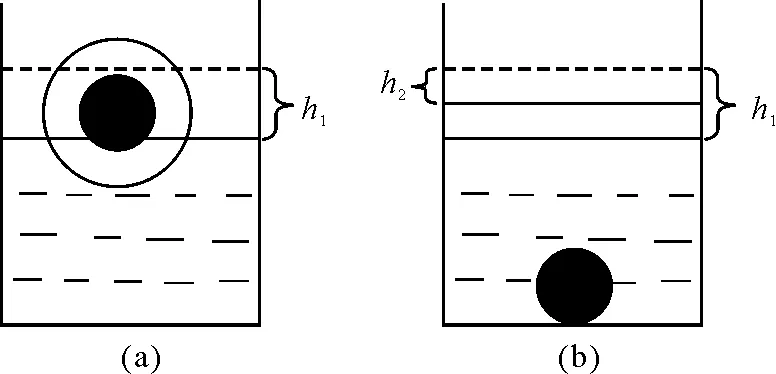
圖4 例5分析圖

由浮力等于重力,應有

ρ水h1Sg=ρ冰V冰g+ρ石V石g

(8)

聯立式(7)、(8)解得

V冰+V石=2.2×10-4m3

(9)

(10)

聯立式(9)、(10)，代入相關數據，解得

V冰=2.1×10-4m3=210 cm3

V石=10 cm3

把上述結果代入式(7)或式(8)解得

ρ石=2×103kg/m3

4 拓展思維提高能力

思維是在表象、概念的基礎上進行分析、綜合、判斷、推理等認識活動的過程．“科學思維”是從物理學視角對客觀事物的本質屬性、內在規律及相互關系的認識方式；是基于經驗事實建構物理模型的抽象概括過程；是分析綜合、推理論證等方法在科學領域的具體運用；是基于事實證據和科學推理對不同觀點和結論提出質疑和批判，進行檢驗和修正，進而提出創造性見解的能力與品格[1]．比如可以讓學生設計下面的實驗，在解決實際問題的過程中拓展思維培養能力．

【例6】給你一只量筒和適量的水，請你設計一個實驗，估測一塊橡皮泥的密度．要求：

(1)寫出實驗步驟及需要測量哪些物理量；

(2)導出用所測量的量表示的橡皮泥密度的數學表達式．

對題目進行分析可以看出，橡皮泥是學生都玩過的物品，生活中常見，作為常識學生應該知道橡皮泥的密度比水的密度大．量筒是實驗室常用的器材，可以用來測體積．要測量橡皮泥的密度，就需要分別測出其質量與體積，在沒有天平的情況下，如何測質量就成為了解決問題的關鍵．如何利用浮力知識解決問題呢？

解答：(1)實驗步驟及需要測量的物理量

1)量筒中倒入適量的水，記下水的體積為V1；

2)把橡皮泥捏成小盒狀，放入量筒中，使其漂浮在量筒中的水面上，記下此時水的體積V2；

3)把橡皮泥捏成實心團使其沉入量筒的水中，記下此時水的體積V3．

(2)橡皮泥密度的數學表達式

推導過程：橡皮泥的重力

G=F浮=ρ水gV2-V1

則

m=ρ水V2-V1

橡皮泥的體積為

V=V3-V1

則

學生面對不同的浮力習題，掌握一般的分析方法，不斷尋求破解浮力難點的鑰匙，不斷取得成功，自信心就會不斷增強．其實解題的一般過程就是由已知指向未知的過程，在由已知到未知的過程中運用所學過的知識和方法，選擇合適的路徑，通過嚴謹的思維，借助自身已有的能力，正確地把已知和未知掛上鉤，問題自然就解決了．