縱向裂紋對盾構隧道襯砌管片力學特性的影響

(核工業西南勘察設計研究院有限公司，四川 成都 610052)

地鐵盾構隧道普遍采用管片作為支護結構。管片在施工與運營過程中容易產生不同程度的開裂與損傷[1]。目前關于管片裂紋的研究，多集中于對其開裂原因與開裂機理的分析。如楊雨冰等[2]基于斷裂力學理論，對管片的開裂破損機制進行了研究；徐國文等[3]基于室內相似模型試驗，采用聲發射測試手段從細觀層面揭示了管片漸進性破壞的全過程；戴志仁[4]對地表大范圍開挖引起下臥盾構隧道管片碎裂的機理進行了分析；盧岱岳等[5]對千斤頂作用下帶榫管片的裂紋擴展規律進行了研究。

1 工程概況

該區間盾構隧道主要穿越膨脹土層和砂卵石地層。隧道管片結構普遍采用“3+2+1”的分塊形式，即襯砌圓環由3個標準塊(B1，B2，B3)、2個鄰接塊(L1，L2)、1個封頂塊(F)組成。管片尺寸見圖1。管片環外直徑6.0 m，內直徑5.4 m，管片厚度0.3 m，幅寬1.2 m。

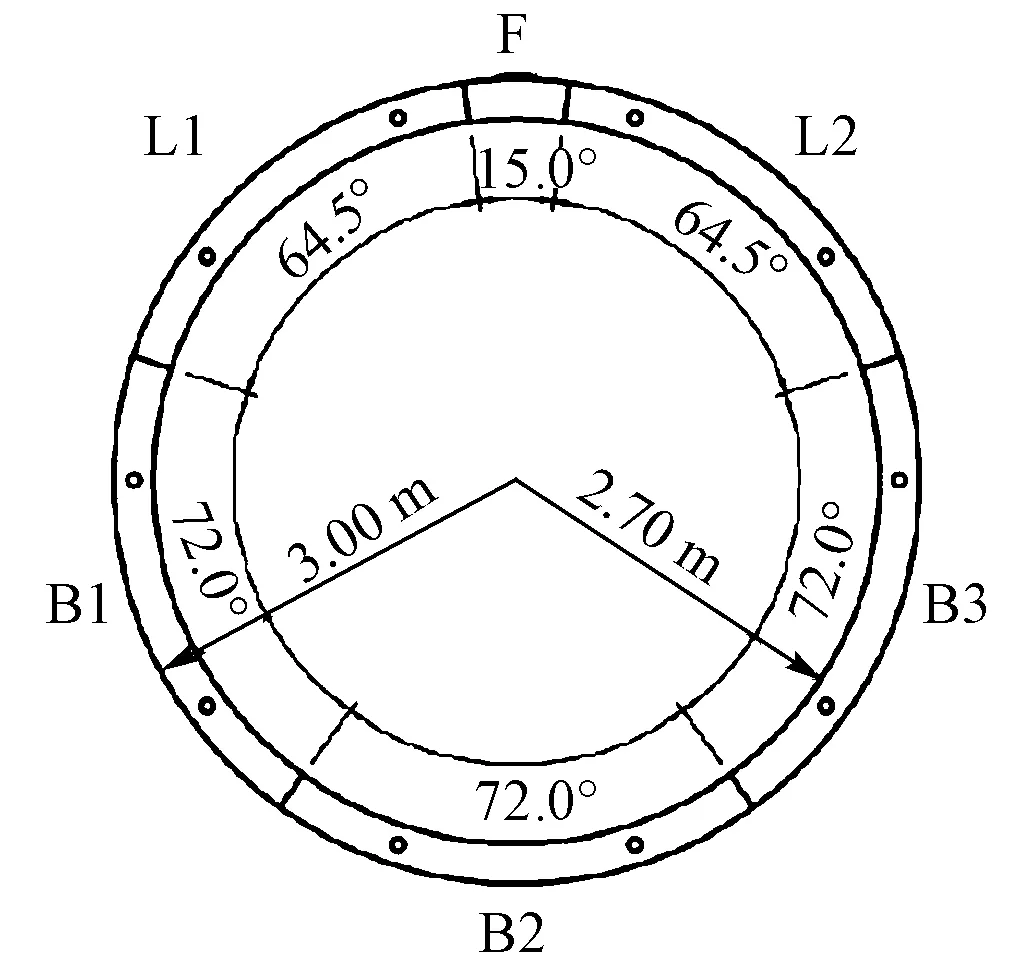
圖1 管片尺寸

隧道運營過程中位于膨脹土層的部分管片產生了沿著幅寬方向分布的縱向裂紋(見圖2)。因此，本文研究縱向裂紋對管片力學特性的影響。

圖2 縱向裂紋

2 數值模擬

2.1 裂損管片模擬方法

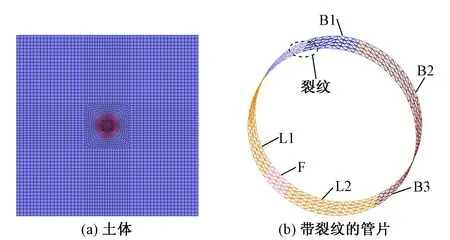
圖3 數值計算模型

管片采用殼單元進行模擬，管片接頭通過彈簧來表征。同時，裂紋采用接頭單元進行模擬[10]，其剛度由Kθ(旋轉剛度)、Kn(剪切剛度)，Kt(抗壓剛度)表征。旋轉剛度的計算公式為

(1)

式中：EI為材料的抗彎剛度；R為盾構隧道的半徑；η為剛度折減系數，η=h/H，h為開裂截面中未開裂部分的高度，H為截面原始高度。

剪切剛度和抗壓剛度的計算公式為

Kn=GA′

(2)

Kt=EA

(3)

式中：G為材料的剪切模量；A為管片截面面積；A′為管片截面的有效面積，A′=ηA。

2.2 計算工況

考慮管片不同裂損程度(η=0.1,0.5,0.7,1)與裂紋位置的組合，分為2種工況進行計算：①裂紋單獨出現在L1，B1和L2塊；②裂紋同時出現在L1，B1和L2塊(單一分塊僅出現單條裂紋)。

2.3 數值模擬的實現

表1 膨脹土層力學參數

3 模擬結果與分析

3.1 覆土厚度的影響

不同覆土厚度下管片內力的分布規律相似。覆土厚15 m與40 m時管片內力分布見圖4。圖中實心圓點為裂紋所在位置，空心圓點為管片環向接頭位置。可以看出：①裂紋的存在會導致裂紋附近內力比無裂紋時明顯減小。覆土厚15 m，裂紋單獨出現在B1，L1，L2塊時，裂紋處彎矩分別為6.7，5.8，22.7 kN·m，小于無裂紋時相應位置的彎矩(37.3，60.2，61.2 kN·m)；裂紋處的軸力分別為400，340，322 kN，也小于無裂紋時相應位置的軸力(849，985，881 kN)。②裂紋的存在并不會改變管片的基本力學特性。外荷載作用下管片全環軸力均為正值(受壓)，且拱頂及拱底處管片內側受拉，拱腰處管片外側受拉。③以裂紋為中心，兩側各25°區域內管片內力受裂紋的影響較大，其余區域內管片內力與無裂紋時相比變化較小。

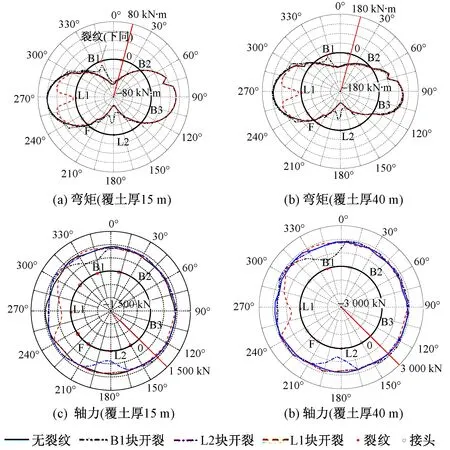
圖4 管片內力分布

3.2 裂損程度及裂紋數量的影響

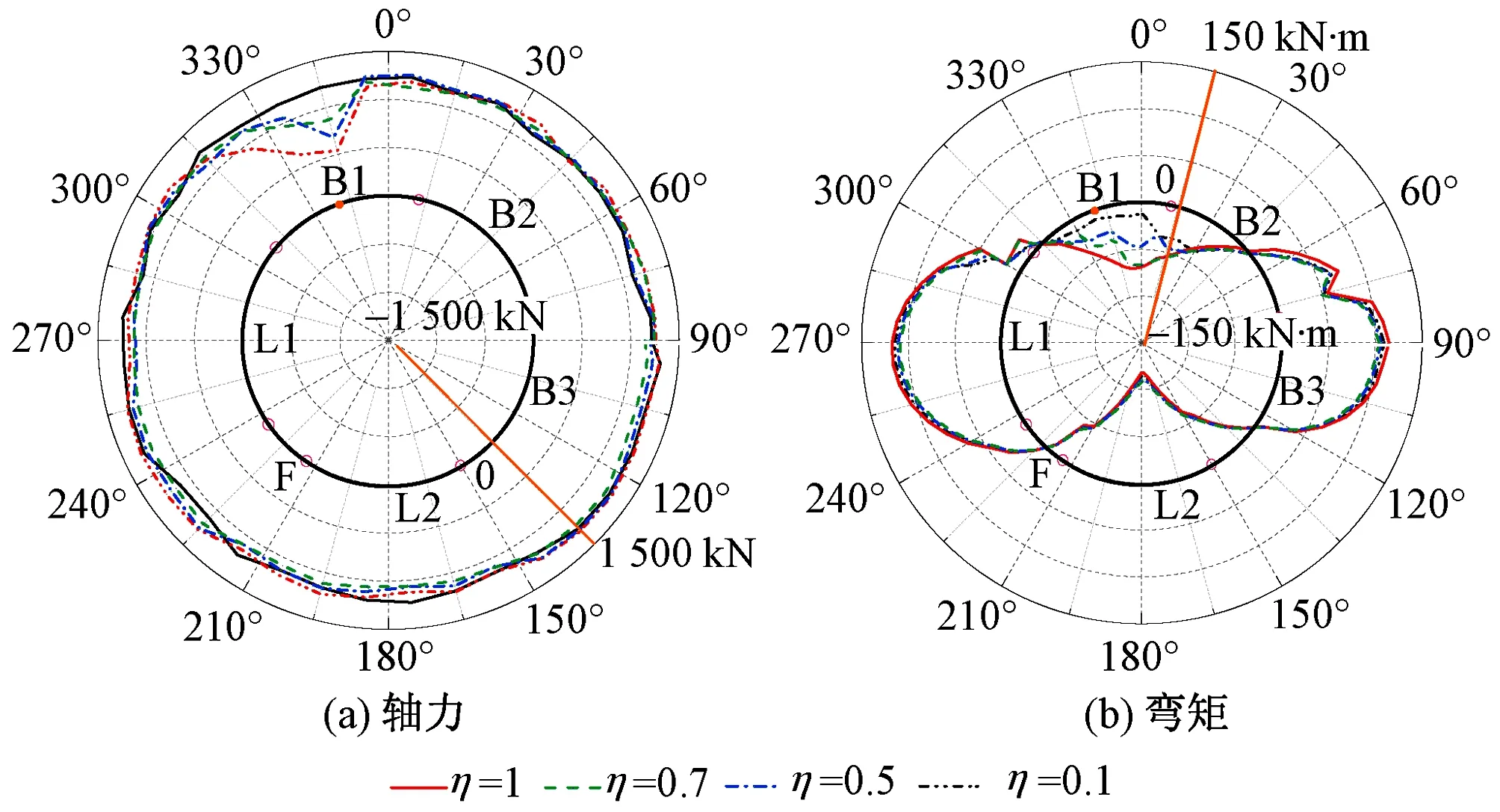
圖5 B1塊存在裂紋時不同裂損程度下管片內力分布

B1塊存在裂紋時不同裂損程度下管片內力分布見圖5。圖中實心圓點為裂紋所在位置，空心圓點為管片環向接頭位置。可以看出：①外荷載作用下管片全環軸力均為正值(受壓)，并未隨著裂損程度的增加出現負值。開裂位置附近管片的軸力均顯著減小，且減小幅度隨著裂損程度的增加而增大。②彎矩受裂損程度的影響規律與軸力類似。③隨著裂損程度的增加，裂紋對管片內力影響較大區域的范圍有所增加。

存在多條裂紋時，裂紋對管片內力的影響規律與存在單條裂紋時相似。不同裂紋數量及裂損程度下管片彎矩分布見圖6。圖中實心圓點為裂紋所在位置，空心圓點為管片環向接頭位置。

圖6 不同裂紋數量及裂損程度下管片彎矩分布

從圖6(a)可以看出:同時存在3條裂紋時裂紋的存在會導致各條裂紋附近管片彎矩比無裂紋時明顯減小。同時，裂紋對管片彎矩影響較大區域的范圍并未產生疊加，在同一裂紋影響區單條裂紋與多條裂紋作用效果相近。

從圖6(b)可以看出：與存在單條裂紋時相似，同時存在3條裂紋時隨著裂損程度的增加裂紋附近管片彎矩逐漸降低，且裂紋對管片彎矩影響較大區域的范圍有所增加。

4 結論

1)裂紋的存在會導致裂紋附近管片的內力比無裂紋時明顯減小。

2)存在多條裂紋時(單一分塊僅出現單條裂紋)，裂紋對管片彎矩影響較大區域的范圍并未產生疊加，在同一裂紋影響區單條裂紋與多條裂紋作用效果相近。

3)隨著裂損程度的增加，裂紋附近管片內力逐漸降低，且裂紋對管片彎矩影響較大區域的范圍也有所增加。