基于廣義斯涅爾定律的聲超常反射

,

(南京航空航天大學 應用物理系, 南京 211106)

當前聲學研究中，超材料的研究是一個熱點問題。所謂的超材料是一種人工復合成的材料，通常由結構尺寸遠遠小于工作波長的單元周期性或非周期性排列組合而成[1-2]。聲學超材料能產生很多自然材料無法產生的特殊物理現象，例如亞波長成像、自準直、超透射、反常多普勒效應[3]、聲波的負折射[4-5]等。聲學超材料的產生無疑給自由調制聲波的設想提供了新思路。筆者正是基于超材料的研究，對傳統的聲反射理論進行了修正，從而實現了聲波的異常反射。

根據傳統的聲學反射理論，當聲波以某個特定角度入射平面時，反射聲波也必定按照同等大小的反射角度出射。如果能夠通過改變反射平面的結構來實現任意反射角的調制，那么在日常生活中會達到意想不到的效果。文章采用的廣義Snell(斯涅爾)定律可以很好地滿足上述要求，該理論通過在反射平面設置特殊的反射相位結構，使得聲波打破原有的規則沿著特定的反射角度出射。根據這一理論，結合COMSOL仿真，設計了一種特殊的聲學微結構來實現180°的相位差，從而控制正入射條件下的反射聲波，且在此基礎上利用3D打印技術對此聲學微結構進行了試驗，仿真和試驗結果成功地驗證了廣義Snell定律。

1 方法論述

Snell定律最初是一條描述光的反射折射規律的定律，是指光從一種介質射向另一種介質時，在界面處會發生反射和折射現象，入射角與折射角的正弦值與入射角無關，而與介質的相對折射率有關[6]。其通常的表達式為

n1sinθ1=n2sinθ2

(1)

式中：n1和n2分別為兩種介質的折射率;θ1和θ2分別為光的入射角和反射角。

由于聲的傳播與波的性質有關，因此該定律同樣適用于聲傳播，其具體的表達式為

sinθr=sinθi

(2)

式中:θr為反射角;θi為入射角。

即聲波在傳輸過程中遇到平面介質發生反射時，遵從反射角等于入射角的定律。

Snell定律作為波傳播的基本理論一直被相關領域的學者所遵循，但是2011年Science上發表的論文對該理論進行了修正，這便是廣義Snell定律[7]。其具體推導見參考文獻[8-11]。

根據費馬原理，光在兩點之間總是按照光程取極值的方向傳播。同時對于光波來說，光程的變化也代表著相位的變化，故光的傳播也需沿著相位取極值的方向[12-14]。

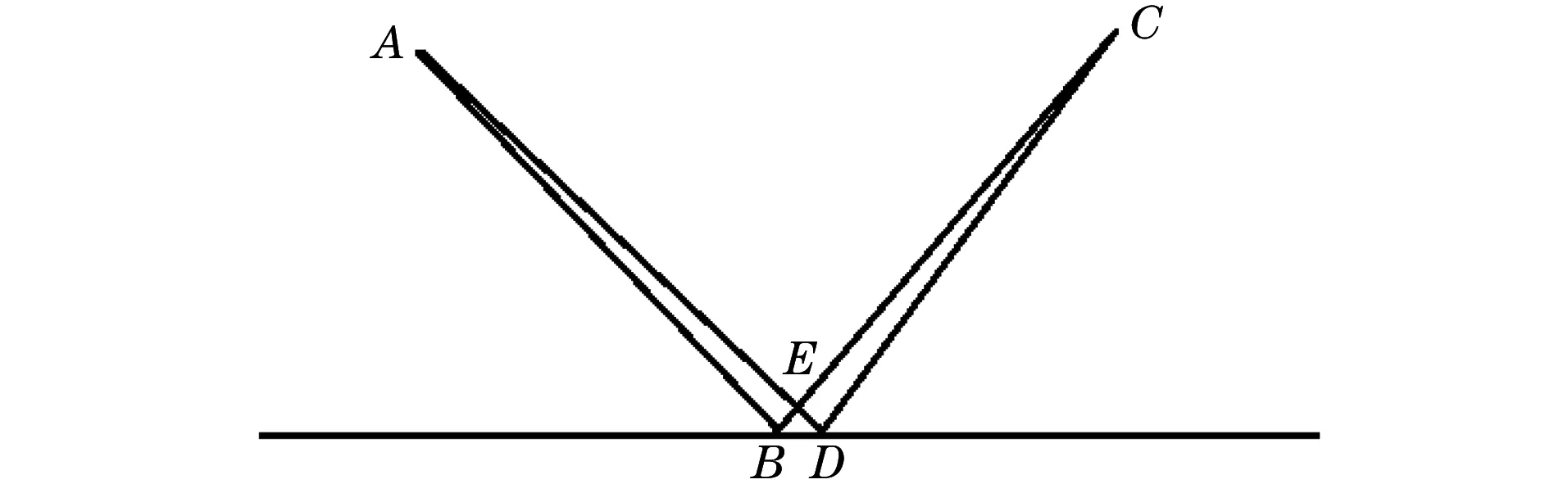
圖1 兩條無限接近的光路示意

兩條無限接近的光路示意如圖1所示，假設光從A點出發經反射界面反射后到達C點。從中選取兩條無限接近的光路ABC和ADC。光經過這兩條光路時產生的相位變化應是相等的，即光在BE這段光程中產生的相位變化與在B點反射時產生的相位變化之和應該等于光在ED這段光程中產生的相位變化與在D點反射時產生的相位變化之和，則有

knsinθidx+φ+dφ=knsinθrdx+φ

(3)

式中：n為折射率;x為聲傳播距離;φ為相位；k為光在介質中的波矢。

整理則有

(4)

式中：λ為光波的波長；dφ/dx為x方向的相位梯度。

由于該定律的推導只利用了光的波動性，基于光聲直接的類比特性，可將廣義的Snell定律應用到聲學領域，即

(5)

式中:dφ/dy為y方向的相位梯度。

若聲波以垂直方向進行入射，廣義Snell定律原理示意如圖2所示，則反射角可表示為

(6)

由此便實現了聲波正入射條件下反射角的偏轉，只需改變入射聲波頻率，便可獲得不同角度的反射角。

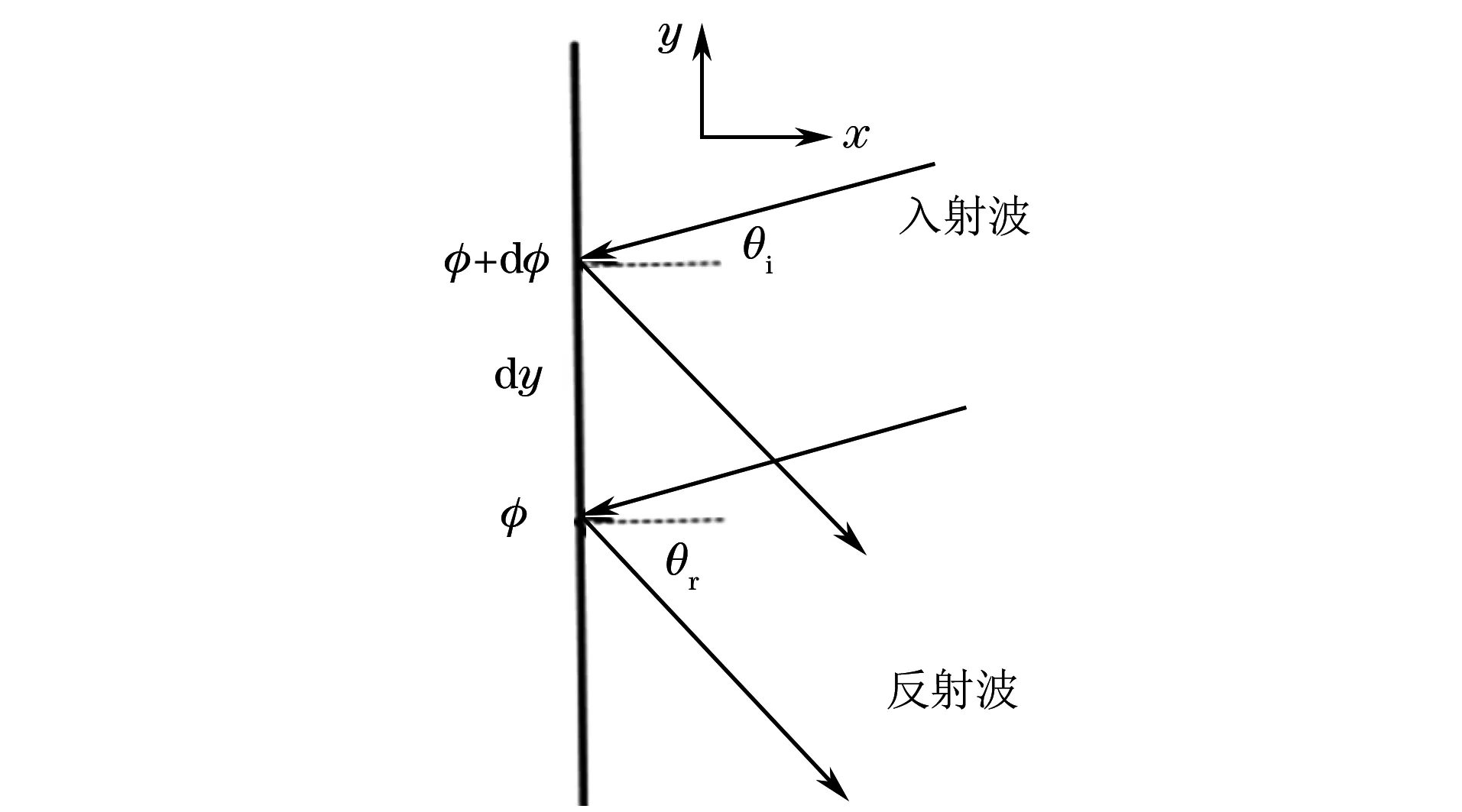
圖2 廣義Snell定律原理示意

2 聲學微結構設計

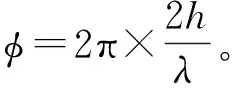
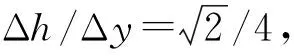
圖3 聲學微結構示意

3 模擬仿真

3.1 模型建立

采用 COMSOL MULTIPHYSICS(以下簡稱 COMSOL)多物理場有限元軟件進行仿真模擬研究[15]。首先設置一個不帶有聲學微結構的聲場。在COMSOL軟件中設置一個半圓形的壓力聲場，半徑設置為7.2 m；在圓心正下方7.2 m處，設置一個長為2.4 m，寬為0.5 m的矩形用以獲得平面波聲源。將邊界條件設置為平面波輻射來模擬無限大空間中的聲場分布，將反射界面設置為硬聲壁，選中矩形的一條長邊，設置其壓力為1 Pa。然后對該聲場進行仿真，發現聲波以垂直方向入射之后會以垂直方向出射。再將上述聲學微結構導入到COMSOL中，放置在圓心處，對有聲學微結構的聲場進行仿真。

3.2 仿真結果分析

圖4為帶有聲學微結構的數值仿真結果，圖中中間處為垂直入射的聲波，兩側為異常的反射聲波。入射波與反射波的夾角約為45°，從仿真結構可以論證上述理論。聲波從垂直方向入射，即入射角為0°，通過該微結構成功實現了出射角為π/4的轉變。由于聲學微結構的對稱性，聲場在左右兩側π/4的位置上均有反射聲波。由此成功論證了廣義Snell定律在聲學中的應用。

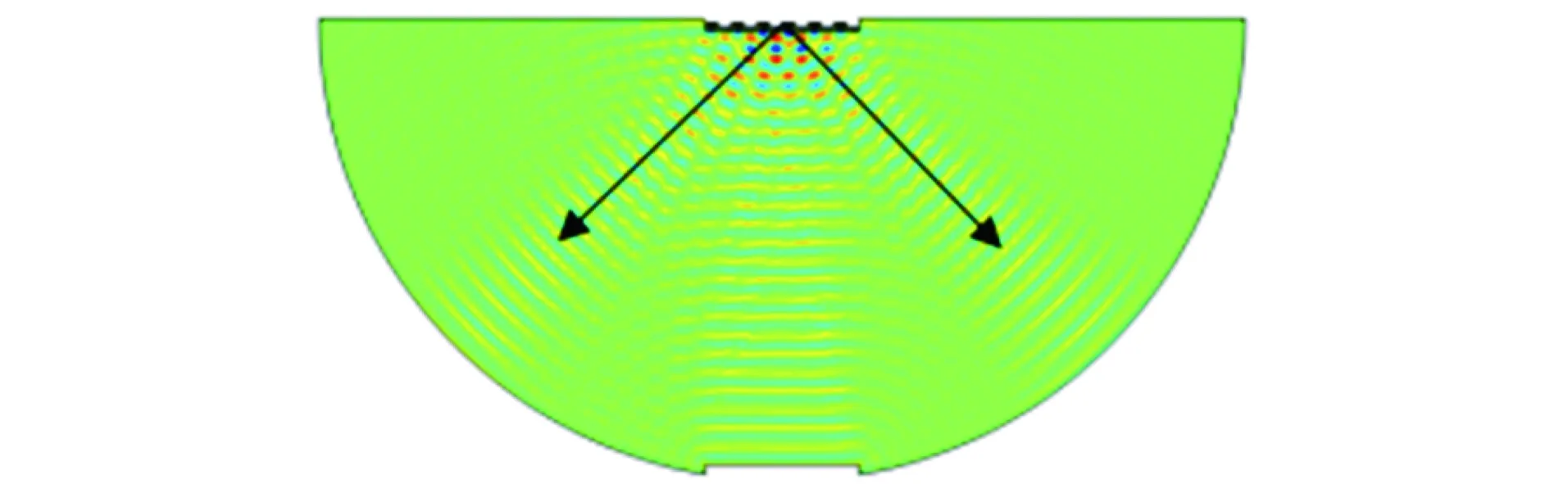
圖4 帶有聲學微結構的數值仿真結果

故可以得出結論，對于給定的聲波頻率，通過設置凹槽的深度和寬度，便可獲得任意的反射角。

4 試驗測量

為了驗證仿真結果的正確性，在對該聲學微結構模型仿真的基礎上，利用易拉罐以及3D打印技術對該結構的聲反射特性進行了測量。

4.1 易拉罐陣列

由于易拉罐罐口很小，罐身很大，在形狀上類似于聲學里由小頸口和大腔體構成的亥姆霍茲共鳴器。根據上面的理論推導，利用兩種不同大小的同類型易拉罐，其制作材料相同，具有相同的截面積和開口大小。這兩種易拉罐的直徑均為6.5 cm，大罐子罐身長17 cm，小罐子罐身長12 cm，若想用這兩種易拉罐達到上述聲學微結構的效果，需要調整聲波頻率。為了讓試驗結果更易分辨，使這兩種易拉罐產生的相位差為π，則從其罐底反射的聲波會干涉相消。聲波垂直入射至易拉罐并從易拉罐底反射所產生的相位差為Δφ=2π(h1-h2)/λ=π時，λ=20 cm，空氣中聲波的速度為343 m·s-1，則該特定頻率為1 715 Hz。由于易拉罐的直徑為6.5 cm，將3個500 ml的易拉罐和3個330 ml的易拉罐排列為一組，重復3組(即為周期排列結構)，此時Δy=19.5 cm，根據計算可得θr=arcsin0.512 8≈π/6。將該模型放置在COMSOL中進行模擬，從仿真結果可看出左右兩側的反射聲壓在π/6處，如圖5所示。然而在垂直出射方向仍存在少部分的反射聲場，這是因為結構陣列表面分辨率過低，兩種凹槽的π的相位差并不能夠完全等效于相位梯度dφ/dy，因此產生的誤差相對較大。

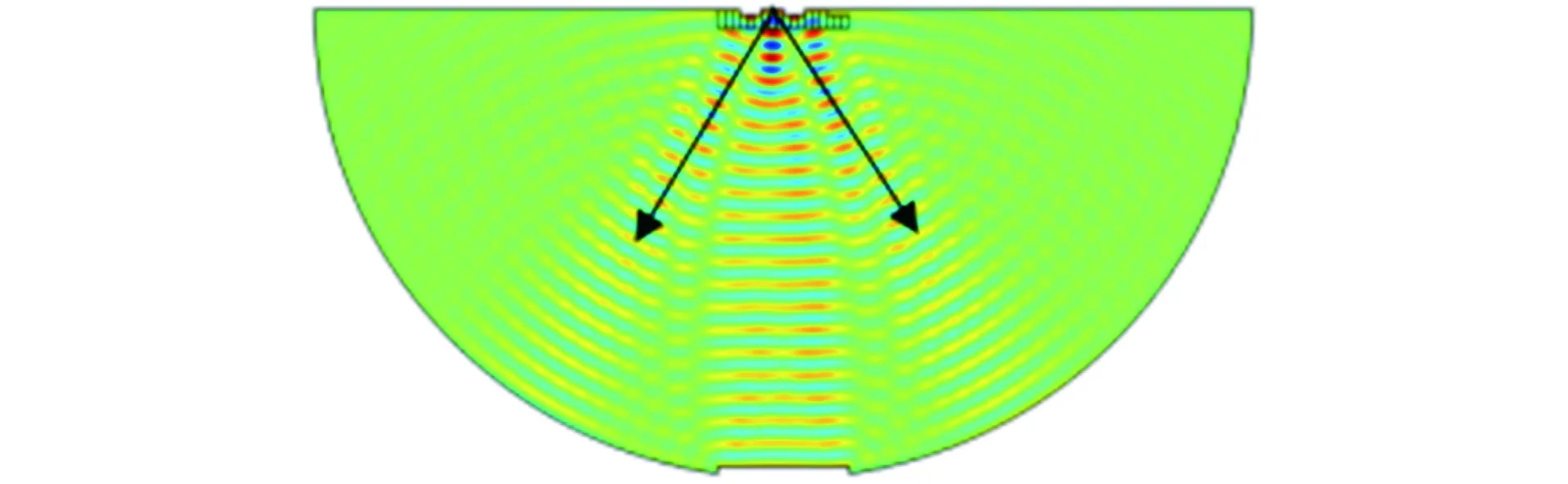
圖5 易拉罐模型的數值仿真結果

為此采用了易拉罐陣列的方法來更好地解決分辨率過低的問題。試驗中采用兩種規格的易拉罐各63個，一個周期內長短易拉罐各排成3列7行，共3個周期，陣列總長約為120 cm，高47 cm。同時保證易拉罐的罐口在同一平面內。

聲信號的發聲裝置由信號發生器和揚聲器構成,信號發生器產生單頻信號驅動揚聲器發聲，將該裝置放于距離易拉罐陣列正前方4 m處，以此來保證聲源發出的聲波以平面波的形式入射到易拉罐陣列。同時將BK傳聲器放置在距離易拉罐陣列表面中心位置2 m處，記錄聲場的聲壓數據，且每隔10°記錄一次。為了減少測量的干擾，試驗全程在消音室內進行。

對于該易拉罐陣列反射聲場的測量，選擇了聲波頻率為1 700 Hz的聲壓，其反射聲指向性如圖6所示。從圖6可看出，易拉罐陣列在1 700 Hz的聲波垂直入射下，反射聲波在33°方向上最為明顯，這個試驗結果和理論仿真的結果相符合，但從圖中可看出在其他方向上也存在少量的反射聲波，這是試驗的器材過于簡單、精確性精準性都不太高造成的。易拉罐陣列試驗驗證了改變聲波反射角的可行性，即可以通過對相位的控制來改變反射聲波的反射角度。但是這種易拉罐陣列操作起來不夠嚴謹，而且易拉罐體積大小都是確定的，很難實現任意的反射角，若想在生活中進行實際應用還不現實。

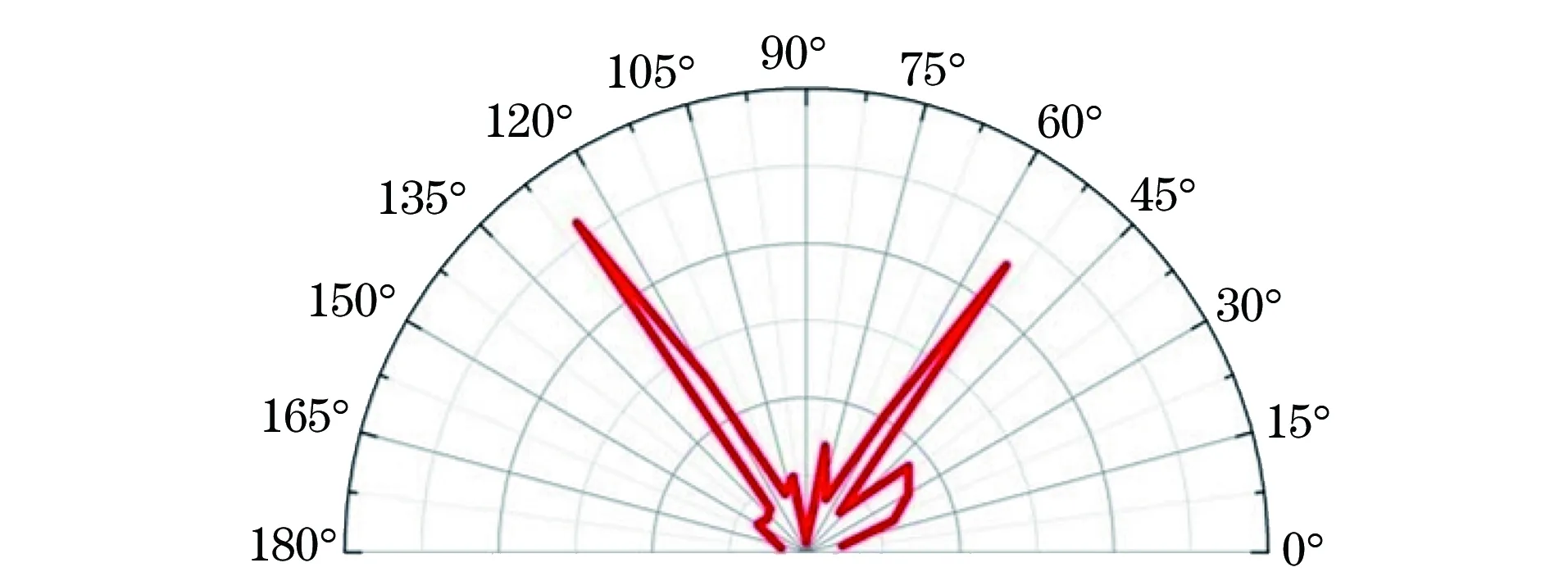
圖6 1.7 kHz聲波入射下的反射聲指向性圖

4.2 3D打印板材聲學微結構

為了保證試驗的準確性和精度，考慮用別的材料來實現這種微結構。結合多種加工技術，充分考慮材料樣品的精度，筆者利用3D打印技術制作了更大面積、更為嚴謹的微結構。該材料樣品共由3部分構成，其最小單元也是圓柱形的凹槽。結構最上面的部分由類ABS塑料粉末經過激光燒結而成，上面開有小孔，上蓋厚度較薄。中間部分的原材料使用的是20 mm的鋁板。結構的最下部分為透明的5 mm聚碳酸酯板，以利于結構內部的觀察。3部分的粘合采用的是0.1 mm厚的雙面膠，粘合后用重物壓合，保證其強度。

該結構的最小單元等同于上述的易拉罐結構，相當于將易拉罐等比例縮小，故仍可實現對某一特定聲波頻率產生特殊的相位變化，從而獲得特定的反射聲場，反射角度仍然滿足廣義的Snell定律。

該結構的最小單元是一個帶有圓柱體空洞的長方體。長方體的長寬均為12 mm，高為22.5 mm，圓柱體半徑為5.5 mm，高為22 mm，開口口徑處的厚度為0.5 mm。對于給定的聲波頻率8 400 Hz，Δy=12 mm，想要實現90°的相位差，根據公式計算可得θr≈58°。若規定陣列中4個單元為一個周期，則每個單元對應的相位差分別為0°，90°，180°，270°。考慮到0°的相位差等同于聲波直接的反射，故第一個單元用平板代替凹槽。其樣品結構如圖7 所示。

圖7 3D打印材料板材樣品結構

將該樣品放置在消音室中，揚聲器放置在距離聲學微結構正前方2 m處的位置，距離樣品1 m處的位置放置傳聲器，仍然是每隔10°記錄一次數據，記錄0°～180°內的反射聲壓。試驗結果如圖8所示,從圖中可看出頻率為8 400 Hz的聲波在60°方向反射聲壓最強，左右兩邊不對稱是板材凹槽傾斜所致。結果與理論計算相符合，驗證了該結構的可行性。

5 結語

利用廣義Snell定律，通過對反射界面結構的設計實現了反射聲波相位的調控，從而在聲波垂直入射條件下可得到任意的反射角，通過理論推導與計算，提出了180°相位差的設計模型，成功使得垂直入射聲波以45°反射角出射。然后選取大小不同的易拉罐對上述理論進行驗證。最后，進一步優化易拉罐的“現成”尺寸，創新地采用 3D 打印技術設計出更精準的板材聲學反射鏡。試驗在專業消聲室中對易拉罐陣列樣品與3D打印板材樣品進行了聲場測量，試驗的偏振角度與理論預測和數值模擬結果都吻合得很好，既證明了理論的正確性，又論證了多種反射角度的偏轉可能性。

該研究意味著通過聲學結構可以實現對聲波的操控，在噪聲控制、醫學超聲、廳堂聲學等領域都有著廣闊的應用前景。但目前來看此設計仍存在一些局限性，設計的聲學微結構只能對單一頻率的聲波發生響應，而實際的聲音包含很寬的頻帶，帶寬的拓寬將是該項工作未來的研究方向。