豪華郵輪主尺度要素統計分析

，，

(大連理工大學 a.船舶CAD中心； b.工程裝備結構分析國家重點實驗室，遼寧 大連 116024)

豪華郵輪是一種高技術、高附加值、高可靠性，以及高要求的船舶，對豪華郵輪進行的研究多集中于豪華郵輪的安全性問題[1-2]以及豪華郵輪的發展近況和趨勢[3-4]，也有部分學者對豪華郵輪的關鍵參數進行了研究[5-6]，但是，少見對豪華郵輪的設計建造等方面進行深入研究的報道。

船舶設計初期要確定主尺度要素，主尺度選擇是否合適直接影響后續設計工作，因此選擇恰當的主尺度尤為重要。已有學者對散貨船、油船、化學品船、起重船、海監船和漁政船等船型的主尺度做了分析和研究[7-8]，但是對豪華郵輪的主尺度還未見研究報道。豪華郵輪主尺度要素的確定還沒有明確的經驗公式或統計公式。為此，搜集188艘豪華郵輪的船型資料，進行統計分析和敏感性分析，運用回歸分析以及神經網絡算法總結擬合程度較好的各主尺度要素的回歸公式。

1 設計特點

一艘新船的設計不僅要考慮其浮性、穩性、耐波性、快速性等性能，還要考慮實際的航道、碼頭港口等情況。船舶性能的實現都與主尺度要素有著密切關系，因此，統計分析豪華郵輪主尺度要素，研究主尺度要素與船舶各性能之間的關系是相當重要的。

隨著豪華郵輪的大型化，其上層建筑的層數會相應地增加，船舶受風面積就會增大，將對完整穩性產生影響，在設計時應充分考慮船舶的完整穩性和破艙穩性。在安全性方面，豪華郵輪還要特別關注消防、撤離和安全返港等問題。為使乘客獲得最大的舒適度，空間的合理分配尤為重要，對振動和噪聲也有嚴格要求。豪華郵輪作為“海上移動城市”，都是沿岸行駛，對環境有一定影響，因此，對廢氣、污水的排放有著嚴格的要求。

2 豪華郵輪主尺度回歸分析

2.1 統計數據分析

從船級社官網查閱資料，獲取了188艘豪華郵輪樣本，去除主尺度信息不全以及主尺度相同的樣本船，選取船型和經濟性較好的139艘豪華郵輪并對其進行主尺度要素的分析。樣本中，船長在150～360 m范圍內；型寬分布在20～40 m；吃水分布在6.0 ～ 9.5 m；總噸位多數分布在10 000 t ～ 200 000 t，樣本船總噸位分布見圖1。

圖1 樣本船總噸位分布

分析樣本可發現，豪華郵輪的吃水隨總噸位的變化不大，維持在6.0～9.3 m之內。在設計過程中，應考慮船體材料的使用，控制吃水，這是決定郵輪是否能在特定港口停泊的重要指標。甲板層數隨著噸位的增加而增加，服務航速在20～22 kn范圍內。乘客、船員人數比值在1.29～3.87范圍內，乘客船員比人數是評價郵輪休閑體驗設計指數的因素之一，該比值越低郵輪的星級等級越高[9]。豪華郵輪的船長型寬比、船長型深比和船長吃水比都較大，表1為統計樣本船的船長Lpp、型寬B、型深D和吃水d的比值范圍。當已知某個主尺度時，可根據該比值范圍對其他主尺度進行粗估。

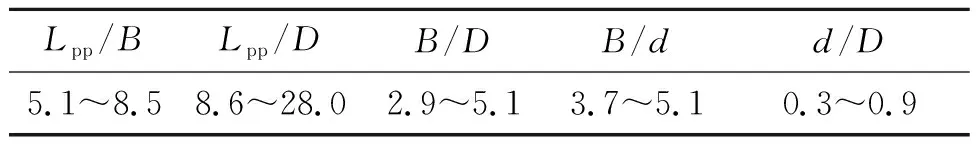
表1 樣本船主尺度比值范圍

2.2 主尺度數學模型的建立步驟

運用統計學方法分析比較樣本數據，剔除明顯不合理的數據；畫出各變量的散點圖，根據散點圖的趨勢，確定數學模型表達形式；再基于最小二乘法，進行回歸分析。為使回歸公式有較高的可信度，首先對變量進行正態評估，表2為統計數據的偏度和峰度。

表2 統計數據的偏度及峰度

偏度是反映變量分布形狀的一個無量綱數值，它度量了分布的偏斜程度及偏向。正態分布的偏度為0，若偏度大于0，則稱分布是右偏；若偏度小于0，則為左偏。峰度是另一個反映變量分布形狀的無量綱數值，它表示分布艉部的厚度。以正態分布為標準，若峰度值大于0，則變量分布的艉部比正態分布的艉部粗；若峰度值小于0，則變量分布的艉部比正態分布的艉部細[10]。

由表2可見，各統計量的偏度和峰度都在一定范圍內，認為統計數據近似服從正態分布。

2.3 敏感性分析

樣本船總噸位數據齊全，為探究主尺度對總噸位影響的重要程度，對他們進行敏感性分析。選擇“Explorer of the Seas”號豪華郵船作為參考船型。該船的主尺度：垂線間長274.7 m，型寬38.6 m，型深11.7 m，吃水8.3 m，總噸位138 194 t。船長對總噸位的敏感度分析見圖2，橫坐標ΔGT/GT0表示樣本船與參考船總噸位的差值ΔGT與參考值GT0的比值，縱坐標ΔL/L0表示樣本船與參考船船長的差值ΔL與參考值L0的比值。根據同樣的方法得到型寬、型深及吃水對總噸位的敏感度，見圖2。

圖2 主尺度對總噸位的敏感度

可以看出,船長和型寬對總噸位的敏感度最為明顯，而型深和吃水對總噸位的敏感度不明顯。各主尺度對總噸位的敏感度系數見圖3。

圖3 主尺度對總噸位的敏感性系數

2.4 單變量回歸分析

根據2.3的敏感性分析可知，各主尺度與總噸位之間都有一定的關系，以總噸位GT為自變量，分別建立各主尺度與總噸位之間的函數關系，各參數回歸結果如下。

1)LPP與GT的回歸公式。

Lpp=3.684GT0.369

(1)

Lpp=80.604 lnGT-664.81

(2)

R2是衡量回歸方程整體擬合度的一個無量綱系數，其值等于回歸平方和在總平方和中所占的比率。R2的值越接近1，說明回歸函數對樣本的擬合程度越好；反之，R2的值越小，說明擬合效果越差。這里認為R2大于0.90時擬合程度較好，其值在0.80～0.90之間表示擬合度一般。式(1)和式(2)的R2值分別為0.95和0.94，說明船長與總噸位的擬合效果較好，式(1)的擬合度優于式(2)，擬合曲線見圖 4。

圖4 船長與總噸位關系

2)B與GT的回歸公式。

B=1.465GT0.576

(3)

B=8.186lnGT-58.922

(4)

式(3)和式(4)的R2值分別為0.95和0.93，型寬與總噸位的擬合度較好，擬合曲線見圖5。

圖5 型寬與總噸位關系

3)D與GT的回歸公式。

D=1.314GT0.184

(5)

D=1.831lnGT-10.123

(6)

式(5)和式(6)的R2值分別為0.83和0.84，型深與總噸位的擬合度一般，擬合曲線見圖6。

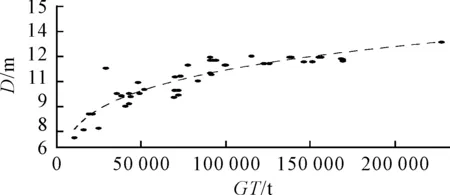
圖6 型深與總噸位的關系

4)d與GT的回歸公式。

d=-1.71×10-10GT2+4.941×10-5GT+5.101

(7)

d=1.361 6lnGT-7.471

(8)

式(7)和式(8)的R2值分別為0.80和0.82，吃水與總噸位的擬合度一般，其擬合曲線見圖 7。

圖7 吃水與總噸位的關系

根據以上的回歸分析初步得到各主尺度關于總噸位的回歸公式。由各公式中的回歸擬合度可以看出，船長、型寬與總噸位的相關性較強，而型深和吃水則與總噸位的相關性較弱。

2.5 多元回歸分析

考慮到各主尺度要素受到多重因素的影響，用多元回歸分析法對這些主尺度要素進行分析。典型的多元線性回歸模型一般形式為

y=β0+β1x1+β2x2+，…，+βnxn+ε

(9)

式中：y為因變量；x1，x2,，…,xn為自變量；β0為常數；β1，β2,，…,βn為回歸系數；ε為隨機誤差。以總噸位為因變量，船長、型寬和吃水為自變量建立回歸模型，得到的回歸公式如下。

GT=-133 854+371LPP+

5 390.55B-5 505.56d

(10)

lnGT=7.543+0.005LPP+

0.057B+0.071d

(11)

式(10)和式(11)的R2值分別為0.94和0.96，多元回歸的擬合度較好。

2.6 BP神經網絡模型

在實際應用中，通常選用三層網絡結構[11]，即輸入層、隱含層和輸出層。

利用MATLAB中的BP神經網絡工具箱對豪華郵輪的主尺度進行分析。將船長、型寬、吃水作為輸入層，總噸位作為目標輸出對樣本進行訓練和預測。首先對原始數據進行歸一化處理，利用train函數對網絡進行訓練，用sim函數對訓練后的網絡進行仿真，最后對結果進行反歸一化處理。BP神經網絡訓練圖見圖8，BP神經網絡預測圖見圖9。

圖8 BP神經網絡訓練圖

圖9 BP神經網絡預測圖

由圖8可見，BP神經網絡的訓練過程表現良好。圖9中，選取的12個測試樣本的測試值與真實值的偏差在±5%范圍內。該神經網絡模型可用于主尺度的預測，設計者根據實際情況對該模型進行變換，在訓練模型中輸入統計樣本的輸入數據和輸出數據，訓練完成后在測試模型中輸入已知參數即可得到所需求的參數。

3 回歸模型驗證

選取5艘未進行回歸分析的豪華郵輪進行誤差分析，這5艘船舶具體資料見表3。

選用回歸分析中擬合度較高的公式以及BP神經網絡模型對這5艘船的主尺度進行計算和預測，并與實際值相比較，見表4。

表3 船舶主尺度

表4 回歸模型結果驗證

從表4中的誤差值可以看出，回歸模型的誤差在±10%范圍內，說明回歸模型有一定的可信性，可為設計者提供參考；由BP神經網絡預測的結果要優于多元回歸模型的計算值。

4 結論

回歸模型以及BP神經網絡模型預測結果較好，適用于船長在150～360 m范圍內，型寬在20～40 m范圍內，吃水在6 ～ 9.5 m范圍內的豪華郵輪的主尺度的預測，為初步設計提供參考。

計算結果還存在一定的誤差，在實際設計過程中應根據具體的船型進行適當修正。根據5艘船型的驗證結果，應用回歸分析和BP神經網絡研究豪華郵輪主尺度要素之間的關系是可行的。