動態網絡社區發現算法研究

胡北辰

(安徽電子信息職業技術學院，安徽蚌埠 233000)

移動通信網絡、淘寶等電子商務網絡、社交網絡等都有一個特性，即它們都是動態的。根據eMarketer的最新統計預測，2017年，80%的中國網民經常訪問社交網絡，大概為6.62億人，其中4.83億網民常用手機訪問社交媒體。如此龐大的網絡結構已經很難憑直觀來挖掘有用的信息，社區發現算法能夠對社區內某些具有共性的信息特征進行分析，使得人們能夠更好地利用社區發現研究結果，例如，在疾病控制中心網中，可以根據社區結構有針對性地加強對疫苗的控制，從而降低成本。

1 經典動態社區發現算法

1.1 GraphScope算法

GraphScope算法[1-3]，是通過合并不同時間片的圖結構從而獲取到新圖，并對生成的新圖應用社區發現。算法的具體過程：判斷新的時間片是否為改變點，若是則開始新的時間片并單獨進行發現社區，且不對網絡的變化進行關注；若不是則合并當前時刻和該時間的圖結構來獲取新的圖，并在新圖中應用社區發現算法，合并后的新圖擁有網絡變化的各時刻信息，同時會持續考慮網絡的動態變化情況。

1.2 FaceNet算法

FaceNet算法[4-6]，是當前時間片t執行社區發現算法，隨之根據t-1時刻來調整時間t的社區結構。該算法分為兩個步驟：首先對當前時間片執行社區發現算法；應用極值優化方法調整t時刻社區結構，將社區結構劃分成二分圖，得到節點相似度矩陣，最終社區發現算法轉化為最小化cost目標函數問題。

1.3 QCA算法

QCA算法[7-8]，是經典的自適應增量式處理網絡動態變化的方法，其t時刻的社區結構是基于上一時刻t-1和t時刻兩者之間的網絡變化而演化生成的。

2 QCA算法的優化

GraphScope算法和FaceNet算法在每一個時間片都需更新網絡圖和重新劃分社區，但一般情況下相鄰的社區不會發生很大的變化，因此這些算法會造成社區劃分計算時間過長。QCA算法應用的是時間片遞增變化處理方法，僅對變化的網絡部分進行計算，因此可以提高算法的效率，但會降低算法的準確率。因此接下來將對QCA算法進行優化。

2.1 符號定義

定義社會網絡是無向圖G=〈V,E〉，V={v1,v2,…,vn}是網絡節點集，vi表示i節點；E={eij|vi,vj∈V,i≠j}是網絡邊集。社區結構為C=C1∪C2∪…∪Ci，i=1,2,…,k，Ci表示i社區。由于動態網絡任一時刻都在變化，因此定義Gt為t時刻的社會網絡，Ct為t時刻的社區結構。

下面首先定義相關的概念：

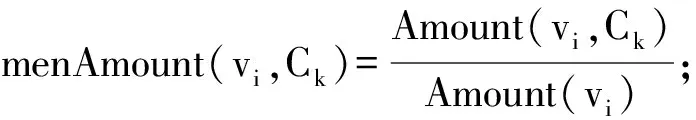
網絡節點vi在Ck的t時刻：Not(vi)=Ck；

當網絡節點vi所在的社區條件發生了變化時，ε是用戶定義的menAmount(vi,Cq)比例值：menAmount(vi,Cq)-menAmount(vi,Cp)≥ε.

2.2 QCA優化

假設在動態網絡的變化過程中，若相鄰的時間片段變化差異較小則表示僅有少量的網絡節點需要重新計算社區劃分。本文著重研究相鄰社區的節點變化，并根據時間片段的前后變化來計算時刻t的社區結構。

2.2.1 增加邊

在t時間段，首先在動態網絡節點a、b中間添加一條邊，且Not-1(a)=Cq,Not-1(b)=Cq，接下來討論添加的邊對各節點的影響。

(1)p=q表示節點a、b在同一社區，和其它的社區沒有連接，且不會對節點所屬社區產生影響，但應加強節點間的聯系來提高緊密性。

(2)p≠q表示節點a、b屬于不同社區。接下來進一步分析節點能否改變社區的劃分：

Amount(a)=Amount(a)+1;Amount(b)=Amount(b)+1;Amount(a,Cq)=Amount(a,Cq)+1，通過節點更新比例值來判斷節點a從Cp轉移到Cq的可能性；

(3)若menAmount(a,Cq)-menAmount(a,Cp)<ε，則節點a不可能轉移到Cq，即接下來討論節點b的可能性：①若Amount(b,Cp)=Amount(b,Cp)+1，則需要看節點b轉移到Cp的可能性；②若menAmount(a,Cq)-menAmount(a,Cp)<ε，則結束當前操作，節點b無法進行移動；③若menAmount(a,Cq)-menAmount(a,Cp)≥ε，則將節點b轉移到Cp，并更新相鄰節點。

2.2.2 刪除邊

若動態網絡中，在t時間段，邊eab將被刪除，接下來討論添加的邊對各節點的影響。

(1)p≠q表示節點a、b屬于不同社區，刪除節點a、b之間的邊不會改變社區，會降低社區間的耦合度，因此僅需更新參數即可。

(2)p=q表示節點a、b為同一社區。①刪除節點a、b之間的邊后，節點a、b分別會成為獨立的社區，則變化過程為：Amount(a)=Amount(a)-1;Amount(a,Cq)=Amount(a,Cq)-1,Amount(b)=Amount(b)-1;Amount(b,Cq)=Amount(b,Cq)-1.C=C∪Ck,Not(a)=Ck，同時更新節點b的社區值，若有某社區Ci符合menAmount(b,Ci)-menAmount(n,Cp)≥ε，則更新節點b的相鄰信息。②刪除節點a、b之間的邊后，并沒有形成社區，因此需重新計算節點a、b的權值來確定它們的歸屬。判斷節點a是否滿足移動要求，若menAmount(a,Cq)-menAmount(a,Cp)≥ε，則更新相鄰的節點，否則對節點b進行判斷，若menAmount(b,Cq)-menAmount(b,Cp)≥ε，則更新相鄰的節點。

2.2.3 添加點

若設在t+1時刻時，在動態網絡中插入節點v，接下來探討兩種情況：

(1)節點v不與任何社區相連，則將節點v設置為社區Ck，且E不變，需要進行如下計算：V=V∪v;C=C∪Ck。

(2)節點v和某一個或多個社區中的一個或多個節點相連。在添加節點v之前，需要計算節點v原來社區的權重值，若Amount(v,Ck)為最大值，則v∈Ck。若網絡中的總社區不變，則設w為v的任一連接節點，需要進行如下計算：V=V∪v;E=E∪evw。

2.2.4 刪除點

若設在t+1時刻時，在動態網絡中刪除節點v，接下來將探討兩種情況：

(1)節點v不與任何社區相連，即?w∈V,?evw?E，則將節點v設置為社區Ck，且E不變，需要進行如下計算：V=V-v;C=C-Ck。

(2)節點v和某一個或多個社區中的一個或多個節點相連，則?w∈V,?evw∈E。若網絡中的總社區不變，設w為v的任一連接節點，需要進行如下計算：V=V-v;E=E-evw。

3 實驗結果分析

將真實的網絡結構作為研究對象，收集動態網絡中電子郵件的發送情況，時間為不同的10個時間段，相鄰的時刻網絡變化極少。通過文獻[9-10]分析可知，當ε=0.1時，社區結構的穩定性和社區特征能夠達到很好的效果。

將動態網絡靜態化，采用GN算法將社區劃分為10個時間的靜態網絡，劃分后的社區結果如表1所示。

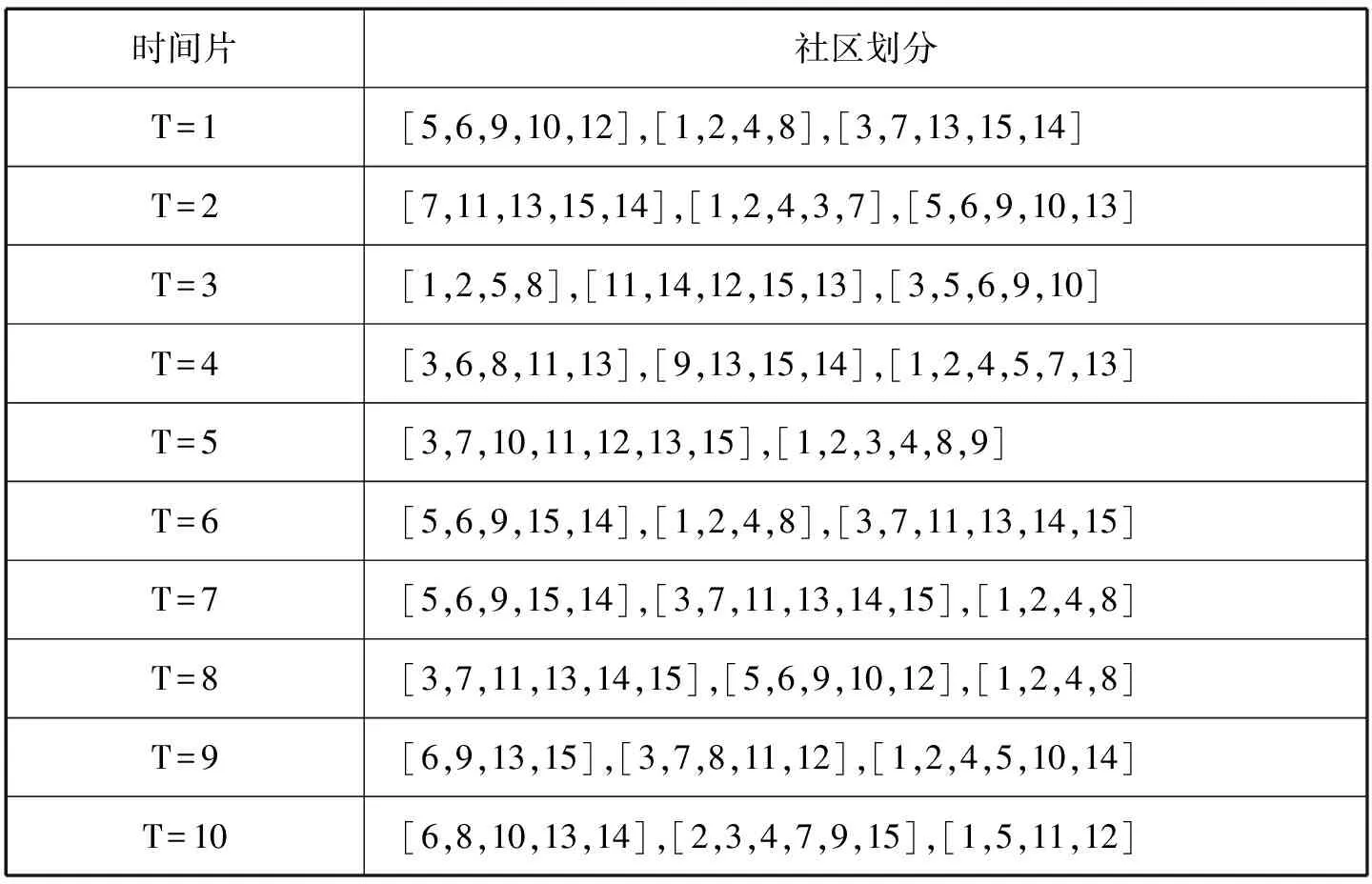
表1 GN社區劃分表

采用優化后的QCA算法與經典的GraphScope算法和FaceNet算法比較社區劃分情況(表2、表3、表4)。

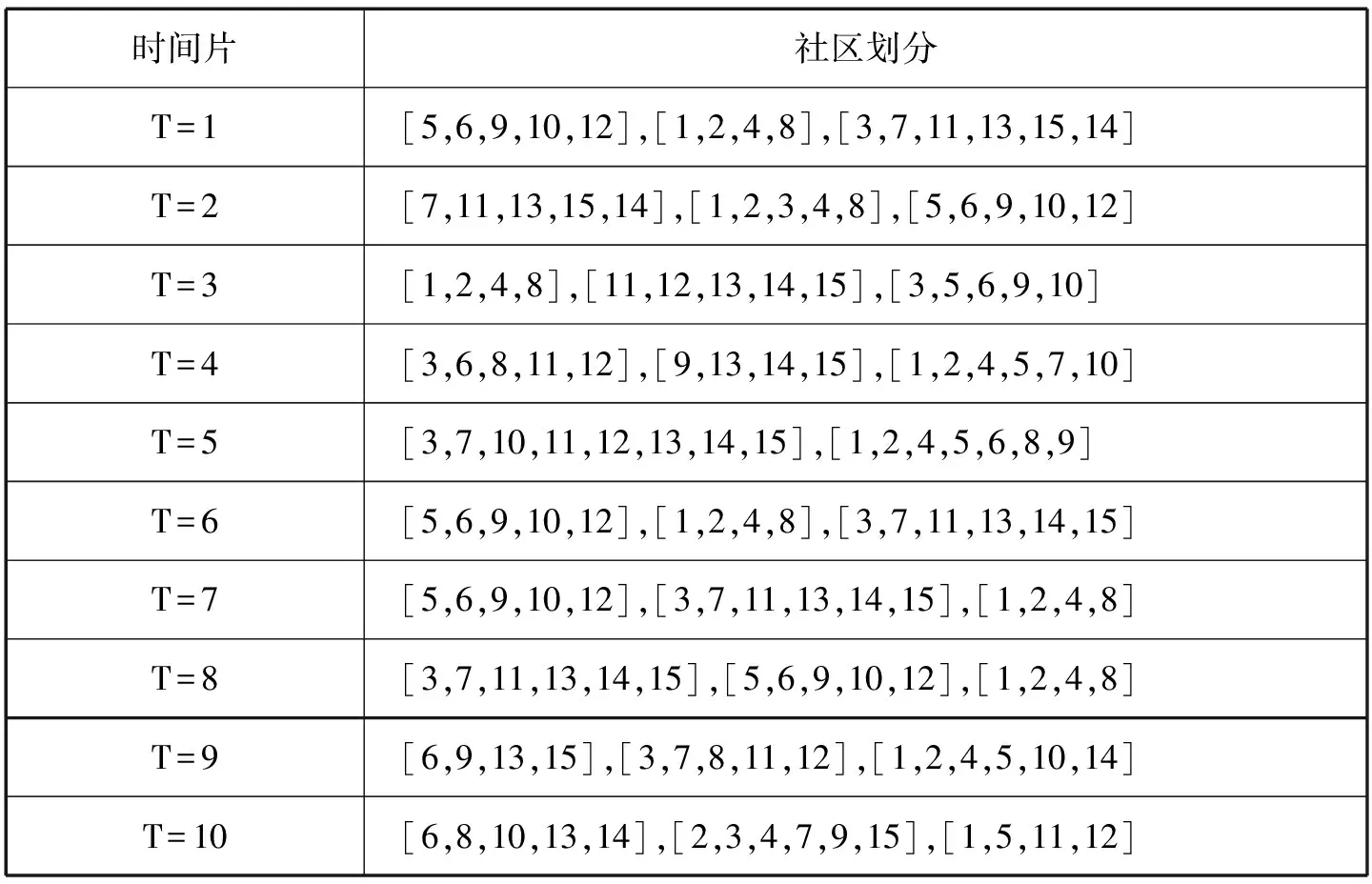
表2 GraphScope算法社區劃分表

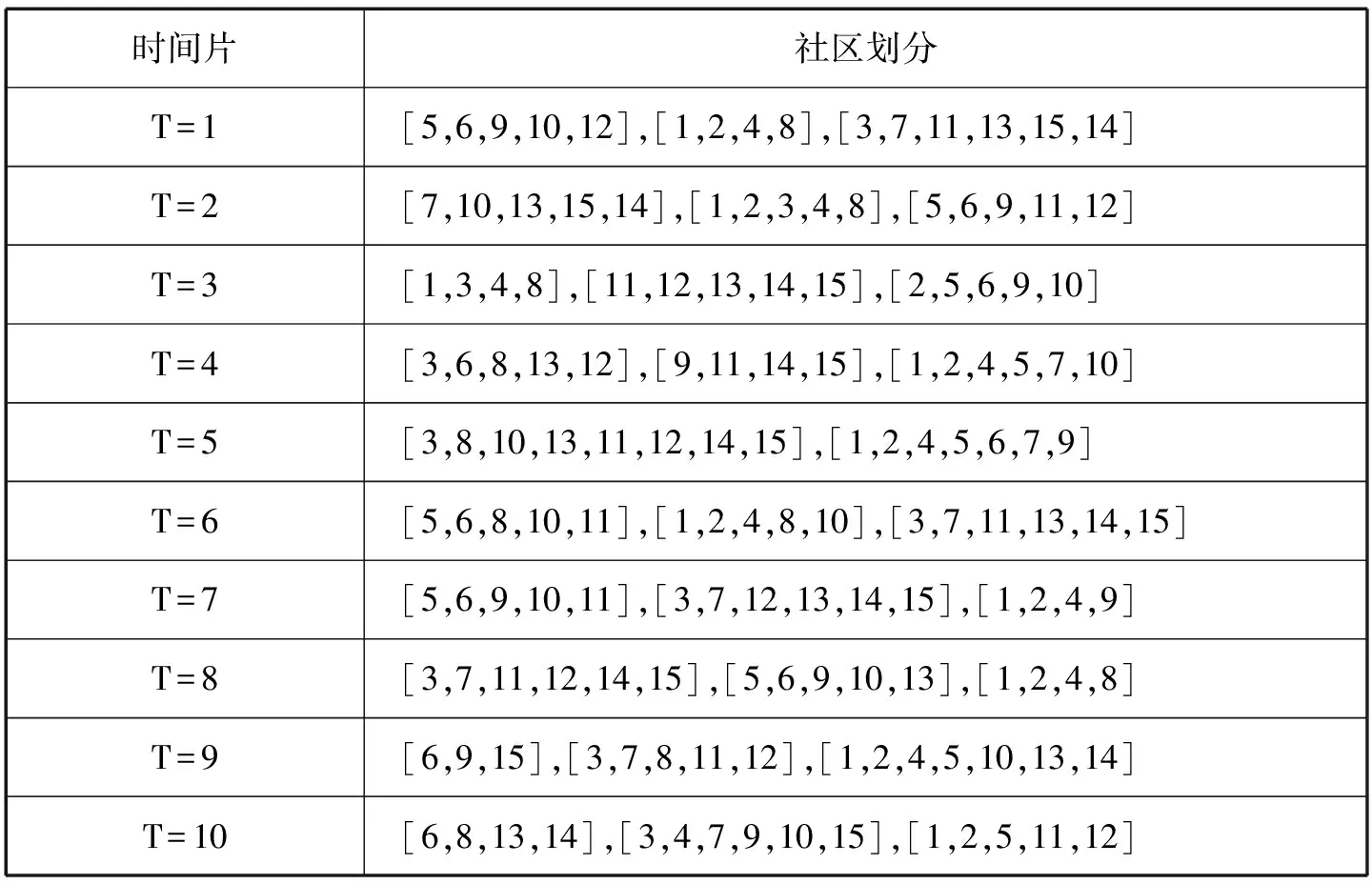
表3 NetFace算法社區劃分表

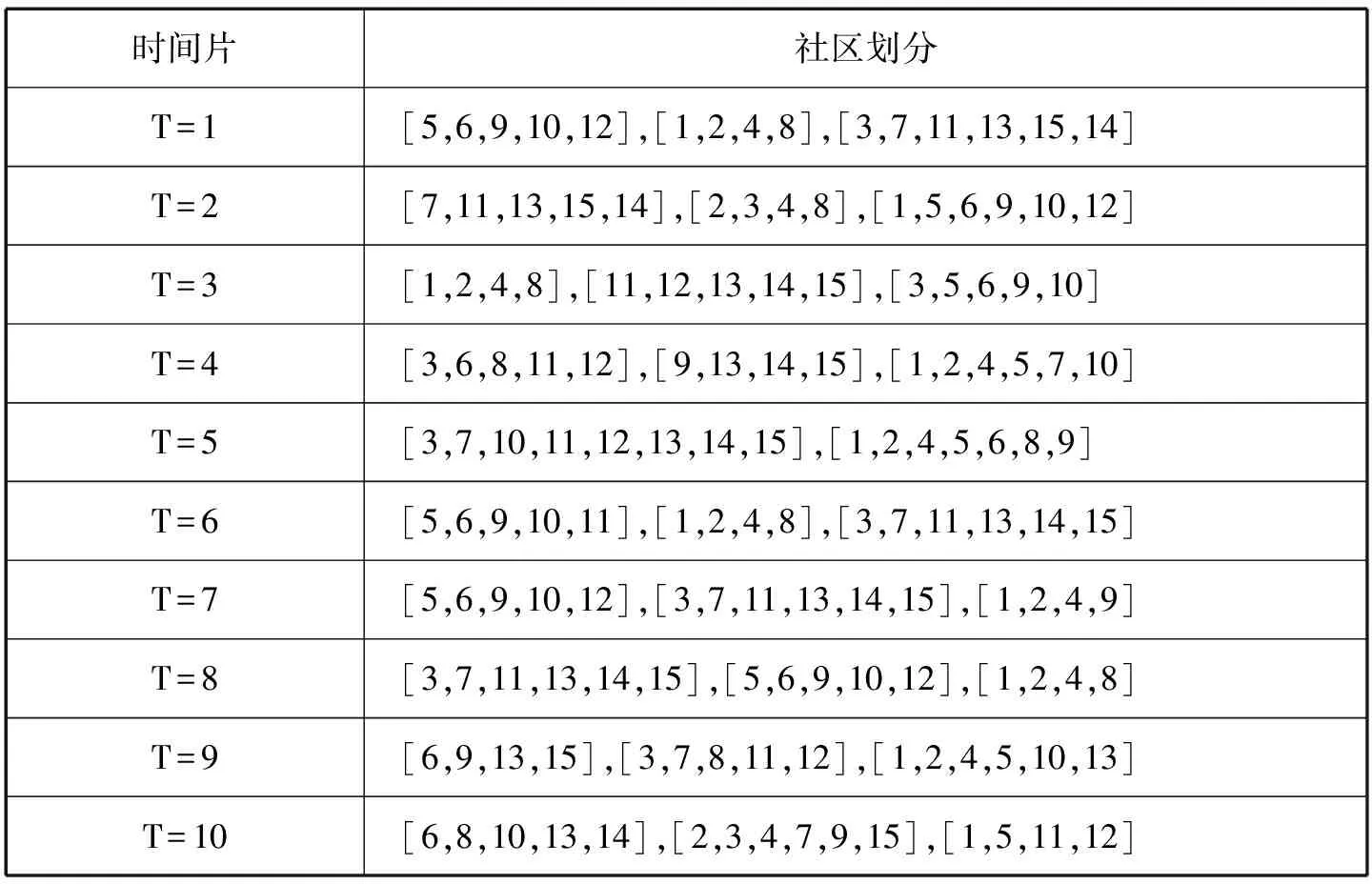
表4 優化后的QCA算法社區劃分表

T=9時刻，GraphScope算法的社區劃分分別為：[6，9，13，15]，[3，7，8，11，12]，[1，2，4，5，10，14]；NetFace算法的社區劃分分別為：[6，9，15]，[3，7，8，11，12]，[1，2，4，5，10，13，14]；優化后的QCA算法的社區劃分分別為：[6，9，13，15]，[3，7，8，11，12]，[1，2，4，5，10，13]。這表明不同的算法劃分的社區是不同的。

運用社區結構質量、準確率、平均時間來直觀地比較各種算法，如表5所示。采用優化后的QCA算法能夠得到較好的社區結構質量、較好的準確率和更少的平均時間。

表5 三種算法比較

4 結語

本文對動態網絡社區發現算法進行研究。首先對經典的社區發現算法進行簡單的介紹，并對經典的OCA算法進行優化，優化后的社區劃分結構質量更佳、準確率較好、計算時間更少。但由于動態網絡的多樣性，還需對算法作進一步的適應性研究。