面向混合數據的多伴隨三支決策

趙天娜，苗奪謙，米據生，張遠健

（1.同濟大學 電子與信息工程學院，上海 201804; 2.同濟大學 嵌入式系統與服務計算教育部重點實驗室，上海201804; 3.河北師范大學 數學與信息科學學院，河北 石家莊 050024）

混合數據[1]是非結構化的、互補的、超高維的，包含大量冗余信息，研究如何有效表示，特征選擇和融合混合數據有重要的實際意義。尤其是在數字化時代，多通道傳感器廣泛化產生，混合數據的分類任務普遍存在于實際生活中，如文本情感分類，醫學影像分析更多復雜的語義以混合屬性值形式表示。數值型和符號型數據的相互作用，導致概念往往具有不一致性和模糊性。如何利用混合數據的上述性質降低此類數據的不確定性是一個值得研究的課題。

模糊粗糙集[2]是一種處理不確定性問題的有效數學工具，然而現有的模糊粗糙集模型不能處理混合數據分類問題。因此，研究模糊粗糙集擴展模型，并應用于混合屬性分類具有重要的理論創新價值。Mi 等[3]用對偶三角模構造邏輯算子，發展了粗糙近似算子的構造方法。Feng 等[4]用概率方法研究并構造了信任函數與似然函數。目前，模糊粗糙近似算子的構造大多使用一對三角模與蘊含算子作為邏輯算子，沒有考慮對象或者屬性之間的差異性。用多伴隨對構造模糊Galois連接，模糊粗糙近似算子，可以體現數值型數據和符號型屬性之間的偏好。近幾年來，Medina 等[5]研究了多伴隨理論，并探究其在多伴隨概念格和多伴隨粗糙集等概念上的應用，但混合數據的表示方面需進一步深入研究。不同類型屬性獲取所需的不同代價問題，是現實生活中數據處理時必不可少要考慮的因素。Tan[6]提出代價敏感學習，并將其應用到許多方面，如遺傳算法[7]、粗糙集[8-9]等。國內學者也研究進展頗豐，如Fan 等[8]針對測試代價敏感決策系統，構造數據模型。Ju 等[10]提出了帶有多粒度指標的代價敏感粗糙集模型。一系列學者都將獲取數據的代價作為數據處理時的重要因素。受上述工作的啟發，本文引入代價敏感多伴隨模糊粗糙集表示數值型屬性和符號型屬性之間的異構互補關系，使得伴隨對與不同類型屬性之間產生關聯；在利用多伴隨算子表達不同類型屬性之間偏好的同時，兼顧了獲取不同類型屬性值的代價。

Yao[11-12]提出的三支決策是處理數據分類任務時基于人類認知的高效決策模式，已有許多專家將其與其他模型結合，大大提高了數據分類能力。Liang 等[13-14]研究了處理多階段信息和雙猶豫模糊信息的基于直覺模糊粗糙集的三支決策模型。Qiao[15]將三支決策引入到推薦系統時，考慮了代價和用戶的偏好，極大改進了推薦質量。徐健鋒[16]以混淆矩陣為工具，多目標優化三支決策閾值求解模型，同時發現了三支決策的代價與決策的條件概率之間存在非單調現象[17]。混合數據分類模型結合三支決策模型的研究已有成果，AL-Hmouz[18]運用三支決策的思想做多模態生物識別系統的開發。趙天娜[19]初步研究了多伴隨直覺模糊粗糙集與三支決策模型的簡單結合。鑒于模型與三支決策組合的優越性，本文將進一步深入地研究用三支決策模型處理混合數據分類問題更優化的方式，代價敏感多伴隨模糊粗糙集模型賦予三支語義，并在決策代價最小化意義下優化混合數據三支分類結果，擴展三支決策理論的應用范圍。

本文的貢獻可從以下幾個方面體現：混合數據的非結構化，互補以及大量冗余無關信息等特點造成數據的高度不確定性，因此數據分類不一致性和模糊性使得挖掘混合數據蘊含的內部信息有難度。找出數值型和符號型屬性之間的各種關系，降低分類的不確定性是混合數據挖掘中亟待解決的問題。針對上述問題，本文用多個伴隨對模擬不同類型屬性之間的關系，多伴隨算子可充分表達不同類型屬性對對象之間的偏好，同時考慮了獲取不同類型屬性值的代價，提出代價敏感多伴隨模糊粗糙集模型。給出充分體現此模型特點的概率公式，并優化了損失函數。改造三支決策模型，挖掘出不同類型屬性的關系特點。針對混合數據的不確定性特點，提出此模型。此模型是數據特點驅動的，從數據本質出發，分析混合數據的特點，找出數值型屬性和符號型屬性之間的各種關系。

1 基本概念

1.1 多伴隨模糊粗糙集理論

Cornelis 等[20]提出的多伴隨模糊粗糙集理論研究了多伴隨對與模糊粗糙集理論結合的基本定義和簡單性質。

定義1[20]給定偏序集(P1,≤1)、(P2,≤2)、(P3,≤3)和映射 & :P1×P2→P3， ↙ :P3×P2→P1，↖:P3×P1→P2， 稱 (&,↙,↖) 是一個伴隨三元組，如果滿足：

1 )對于x∈P1,y∈P2,z∈P3， 都有x≤1z↙y?x&y≤3z?y≤2z↖x；

2) & 在P1、P2、P3上是保序映射；

3) ↙ ,↖ 在第1 和第2 論域上是保序映射。

定義2[20]設 (L1,L2,P,&1,···,&n) 是多伴隨框架，稱 (A,U,R,τ) 為多伴隨背景，其中A是非空對象集，U是非空屬性集，R:A×U→P是P-模糊關系，滿足自反性和對稱性。τ:A×A→{1,2,···,n}是將A×A中元素對映射到多伴隨框架上一個特定的伴隨三元組。

定義3[20]在模糊決策信息系統(U,A∪g0gggggg)中，給定屬性子集B?A， 和P-模糊關系Ra:X×X→P,?a∈A, 對于x,y∈U，模糊關系RB:U×U→P定義為：

@:Pm→Pa∈A

其中 是一個聚合算子，對于 ，有

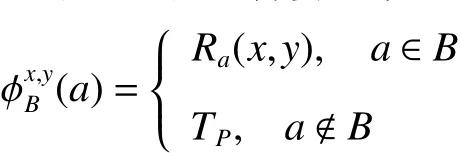
其中TP是P的最大值。

定義4[20]在多伴隨面向屬性框架(P,L,L,&1,···,&n) 下，考慮形式背景 (U,U,RB,τ)， 對于x,y∈U，定義似然算子 ↑π:LU→LU和必然算子 ↓N:LU→LU

那么g↑π

是g的上近似，f↓N是f的下近似。其中LU表示所有由U映射到L的函數的集合。

定義5[20]對于模糊子集h∈LU， (h↓N,h↑π) 稱為多伴隨模糊粗糙集。

1.2 基于決策粗糙集的三支決策

決策粗糙集模型用狀態集和行動集來描述決策過程。狀態集 ? ={C,?C} 中的2 個狀態分別表示某事件屬于C和不屬于C， 行動集A={aP,aB,aN}分別表示接受某事件、延遲決策和拒絕某事件3 種行動，用λPP、λBP、λNP；λPN、λBN、λNN表示采取不同的行動會產生不同的損失，分別表示當x屬于C或x不屬于C時采取行動 A ={aP,aB,aN} 的損失。采取3 種行動的期望損失函數由如下式子表示：

根據貝葉斯決策規則，以期望損失函數最小為原則選擇最佳行動方案，決策規則如下：

(P) 若R(aP|[x])≤R(aB|[x]) 且R(aP|[x])≤R(aN|[x])，則x∈POS(C) ；

(B) 若R(aB|[x])≤R(aP|[x]) 且R(aB|[x])≤R(aN|[x])，則x∈BND(C) ；

(N) 若R(aN|[x])≤R(aP|[x]) 且R(aN|[x])≤R(aB|[x])，則x∈NEG(C)。

2 代價敏感多伴隨模糊粗糙集

混合數據的數值型和符號型屬性是由多通道傳感器產生的，獲取途徑差異很大，采集不同類型屬性付出的代價均不相同。在現實生活中，考慮經濟因素，研究人員希望用幾個代價較小的屬性，提取同樣有價值的信息，因此不同類型的屬性代價是必不可少要考慮的因素。本文希望用更少的代價獲取更有價值的信息。

定義6設A?=(U,A∪D) 是混合數據決策系統，U是非空論域，A∩D=?，A=AS∪AR，AS= {a1,a2,···,ai,···,am} 和AR={am+1,am+2,···,am+i,···,am+n}分別是符號和數值型條件屬性的集合。獲取對象x分別關于不同模態屬性AS和AR的信息付出的代價為 Co str、 CostR。考慮模態屬性代價得到的權重wC定義如下：

i

1) 對于ai∈AS,i∈{1,2,···,m}，每個屬性的權重定義為:

2) 對于ai∈AR,i∈{m+1,m+2,···,m+n}，每個屬性的權重定義為：

定義7 設A?=(U,A∪D) 是混合數據決策系統，U是非空論域，A∩D=? ，對于a∈A，a-模糊關系Ra:U×U→[0,1] 定義如下：

?B?A，B- 模糊關系定義如下：

性質1滿足自反性和對稱性。

證明1)由的定義可知，Ra(x,x)=1，進而推出(x,x) =1。因此，CB滿足自反性。

性質2滿足單調性，即

證明1)若B1=B2， 則顯然

2) 若B1?B2，則必存在ai∈B2，但是ai?B1。由則對于其他屬性aj∈B1∩B2=B1， 有成立。由的定義可知

定義8在多伴隨面向屬性框架(P,L,L,&1,···,&n) 下，考慮有代價的形式背景對于m∈LU，定 義似 然算 子 ↑π:LU→LU和 必 然 算 子↓N:LU→LU：對于x,y∈L

對于模糊子集m∈LX，稱為代價敏感多伴隨模糊粗糙集。

經過對代價敏感多伴隨模糊粗糙集的研究，本文發現，添加一個簡單條件后，它仍滿足經典的粗糙集中上下近似的性質。由性質1 和性質2 可知，本文定義的關系滿足文獻[13]中關系RB的性質，因此，本文中代價敏感多伴隨模糊粗糙集的上下近似需添加的條件和文獻[7] 中3.2中命題1 的條件一致。

m∈LU

性質3對于 ，

證明過程可參照文獻[12]中3.2 中命題1 的證明。

3 基于代價敏感多伴隨模糊粗糙集的新型三支決策模型

基于決策粗糙集的經典三支決策模型利用狀態集 ? ={C,?C} 和行動集 A ={aP,aB,aN} 描述決策過程。采取不同的行動產生不同的損失函數矩陣如 表1 所示， 這些 損 失函數 滿 足λPP＜λBP＜λNP；λNN＜λBN＜λPN，其中λ??∈(0,1)。

表1 經典模糊損失函數矩陣Table 1 Classical fuzzy loss function matrix

由經驗可知，對象屬于狀態集的概率直接影響決策過程。在三支決策模型中，體現為概率是定義決策目標函數(期望損失函數) 的關鍵因素。因此，給出體現模型特點的概率定義對精確決策至關重要。

在經典的三支決策模型中，代價與決策的條件概率是單調的線性關系，如圖1，但在實際生活中，三支決策的代價與決策的條件概率之間存在著非單調情況[17]，如圖2，針對這種現象，徐健鋒等[17]以延遲代價目標函數為研究對象，提出了一種雙延遲代價目標函數的策略。本文借鑒這一思想，在代價敏感多伴隨模糊粗糙集模型上，給出充分貼近此模型特點的概率定義，并優化做延遲決策aB時的非線性損失函數，期望得到更準確處理分類任務的三支決策模型。

圖1 經典三支決策 F N、FP、FB 的線性關系Fig.1 Classical linear relation diagram of three decisions

圖2 新型三支決策 F N,FP,FB′,FB′′ 的非線性關系Fig.2 Novel linear relation diagram of three decisions

3.1 改進的三支決策模型

改進的三支決策模型，與傳統三支決策模型相比，λPP、λPN、λNP、λNN定義不變，只改進、和如表2，它們的含義為：分別從正域和負域視角出發，實際為正域元素和負域元素但決策時被劃分為延遲域的2 組代價函數。正域決策代價目標函數FP、 負域決策代價目標函數FN不變，只改進雙延遲決策代價目標函數，記為、。由于非線性函數FB有很多種定義方式，不同的定義方式導致不同的非線性函數FB，為了簡化和一般性，本文選取最簡單的非線性模型進行說明，由這2 個線性函數組成一個非線性函數，并假設本文只討論圖2 這種非線性的情況。其他情況類似，在此不再贅述。

表2 新型模糊損失函數矩陣Table 2 New fuzzy loss function matrix

多伴隨模糊粗糙集充分考慮了數值型和符號型屬性之間的互補性、關聯性、大量無關冗余信息的特點，用此模型從混合數據中提取的蘊含信息高效體現對象屬于狀態集的可能性程度。本文用3 種策略描述對象屬于狀態集的概率。

定義9(平均概率)對象x屬于狀態集C的平均概率定義為：

定義10對象x分別采取 A ={aP,aB,aN} 3 種行動的平均模糊期望損失函數計算公式為：

定義11(悲觀概率)對象x屬于狀態集C的悲觀概率定義為：

定義12對象x分別采取 A ={aP,aB,aN} 3 種行動的悲觀模糊期望損失函數計算公式為：

比較F(aP|x)P、F(aB|x)P、F(aN|x)P的大小，確定行動ai(i∈{P,B,N}) 使悲觀模糊期望損失函數FP最小。

定義13(樂觀概率)

定義14對象x采取 A ={aP,aB,aN} 3 種行動的樂觀模糊期望損失函數計算公式為：

4 基于代價敏感多伴隨模糊粗糙集的三支決策算法

比較F(aP|x)O、F(aB|x)O、F(aN|x)O的大小，確定行動ai(i∈{P,B,N}) 使樂觀模糊期望損失函數FO最小。

算法1基于代價敏感多伴隨模糊粗糙集的

本文提出的基于代價敏感多伴隨模糊粗糙集的三支決策算法，是處理具有偏好的模糊信息的不確定性決策理論，以最小期望損失為目標，得到損失最小的決策。

本文僅以樂觀概率為例給出混合數據分類的基于代價敏感多伴隨模糊粗糙集的三支決策算法。整個算法流程圖，如圖3 所示。樂觀三支決策算法

圖3 三支決策算法的流程Fig.3 Flow chart of three decision algorithms

輸入混合數據決策表 (U,A∪D)，屬性代價CostS, C ostR， 模糊集m，損失函數矩陣λ。

輸出行動集，分類精度 A cc。

2) For 每個對象x∈U

比較期望損失函數Fai,i∈{P,B,N}，選擇期望損失Fai最小的行動集ai作為最佳行動方案；

End For

5 實例驗證

設混合數據的決策表 (U,A∪D) 如表3，獲取符號型屬性和數值型屬性的代價比為CostS:CostR=1，則由定義6 得每個符號型屬性和數值型屬性的權重分別為由定義7 得到模糊關系如表4 所示。

表3 混合數據的決策表Table 3 Decision table of heterogeneous data

設每個對象對應的m(x) 的值分別為：0.76、0.17、0.15、0.76、0.53、1、0，由定義8，利用Godel t 模和相應的蘊含算子構造的伴隨對 ( &G,↙G,↖G)，Product t 模和相應的蘊含算子構造{的 伴隨對(&P,↙P,↖P)， 其中得到代價敏感多伴隨模糊粗糙集為：

由對象屬于狀態集的概率的定義11，得P(x1) =0.76、P(x2) = 0.17、P(x3) = 0.15、P(x4) = 0.76、P(x5) =0.53、P(x6) = 1、P(x7) = 0。

參照徐健鋒[16]中雙延遲代價雙量化三支決策模型第4 章模型1 的參數：

表4 模糊關系Table 4 Fuzzy relation

表4 模糊關系Table 4 Fuzzy relation

RC B x1 x2 x3 x4 x5 x6 x7 x1 0.5 0.375 0.375 0.5 0.375 0.5 0.5 x2 0.375 0.5 0.5 0.375 0.5 0.375 0.375 x3 0.375 0.5 0.5 0.375 0.5 0.375 0.375 x4 0.5 0.375 0.375 0.5 0.375 0.5 0.5 x5 0.375 0.5 0.5 0.375 0.5 0.375 0.375 x6 0.5 0.375 0.375 0.5 0.375 0.5 0.5 x7 0.5 0.375 0.375 0.5 0.375 0.5 0.5

以代價風險函數最小為原則，得到數據分類規則為：

得到數據分類如表5 所示，由此可知分類精度為85.7%。

表5 是分別采用樂觀概率，悲觀概率，平均概率時，對每個對象的采取決策的結果，從結果可知，依據3 種概率得到的期望損失函數的判斷結果是一致的。

表5 樂觀、悲觀、平均概率情況下數據分類結果Table 5 Data classification results in positive, negative, average cases

6 結束語

混合數據的分類問題是研究熱點。本文從混合數據的模糊性和符號型、數據型屬性的不一致性等特點出發，利用多伴隨，模糊粗糙集給出不同類型屬性之間的不同度量，考慮不同類型屬性的代價，期望花費最小的代價得到最有價值的信息。在延遲代價雙量化的基礎上，研究了多種不同的模糊概率策略，構造了混合數據分類過程中的三支決策模型。該模型既能反應出數據本身的客觀不確定性，也可以表達決策者主觀上對不同類型屬性的偏好及數值型和符號型屬性數據獲得難易程度的認識。未來可繼續研究更多的模糊粗糙集的擴展模型，期望在超大規模數據集上刻畫混合數據的精確表示，挖掘出更多數據內部蘊含的信息。