基于模糊核聚類粒化的粒度支持向量機

黃華娟，韋修喜，周永權,2

（1.廣西民族大學 信息科學與工程學院，廣西 南寧 530006; 2.廣西民族大學 廣西高校復雜系統與智能計算重點實驗室，廣西 南寧 530006）

支 持 向量 機(support vector machine, SVM)自1995 年由Vapnik 提出以來就受到理論研究和工程應用2 方面的重視，是機器學習的一個研究方向和熱點，已經成功應用到很多領域中[1-3]。SVM 的基本算法是一個含有不等式約束條件的二次規劃(quadratic programming problem, QPP)問題，然而，如果直接求解QPP 問題，當數據集較大時，算法的效率將會下降，所需內存量也會增大[4-8]。因此，如何克服SVM 在處理大規模數據集時的效率低下問題，一直是學者們研究的熱點。

為了更好地解決大規模樣本的分類問題，基于粒度計算理論[9-10]和統計學習理論的思想，Tang 等于2004 年首次提出粒度支持向量機(granular support vector machine, GSVM)這個術語。GSVM 的總體思想是在原始空間將數據集進行劃分，得到數據粒。然后提取出有用的數據粒，并對其進行SVM 訓練[11-12]。與傳統支持向量機相比，GSVM 學習機制具有以下優點：針對大樣本數據，通過數據粒化和對有用粒子(支持向量粒)的提取，剔除了無用冗余的樣本，減少了樣本數量，提高了訓練效率。然而，Tang 只是給出了GSVM 學習模型的一些設想，沒有給出具體的學習算法。2009 年，張鑫[13]在 Tang 提出的GSVM 思想的基礎上，構建了一個粒度支持向量機的模型，并對其學習機制進行了探討。此后，許多學者對支持向量機和粒度計算相結合的具體模型進行了研究，比如模糊支持向量機[13]、粗糙集支持向量機[14]、決策樹支持向量機[15]和商空間支持向量機[16]等。但這些模型的共同點都是在原始空間直接劃分數據集，然后再映射到高維空間進行SVM 學習。然而，這種做法很有可能丟失了大量包含有用信息的數據粒，其學習算法的性能會受到影響。為此，本文采用模糊核聚類的方法將樣本直接在核空間進行粒的劃分和提取，然后在相同的核空間進行GSVM 訓練，這樣保證了數據分布的一致性，提高了算法的泛化能力。最后，在標準UCI 數據集和NDC大數據上的實驗結果表明，本文算法是可行的且效果更好。

1 粒度支持向量機

張鑫[17]在Tang 提出的GSVM 思想的基礎上，構建了一個粒度支持向量機的模型。

設給定數據集為X={(xi,yi),i=1,2,···,n} ，n為樣本的個數；yi為xi所屬類的標簽。采用粒度劃分的方法(聚類、粗糙集、關聯規則等)劃分X，若數據集有l個類，則將X分成l個粒，表示為：

若每 個粒包含li個點 ，Yi表示第i個粒的類別，則有：

其中：

則在GSVM 中，最優化問題變為：

將上述問題根據最優化理論轉化為其對偶問題：

當數據集是線性不可分時，GSVM 不是在原始空間構造最優分類面，而是映射到高維特征空間，然后再進行構造，具體為：

將X從 Rn變換到 Φ：

以特征向量 Φ (X) 代替輸入向量X，則可以得到最優分類函數為：

利用核函數來求解向量的內積，則最優分類函數變為：

其中，k(Xi,X) 為粒度核函數。當ai＞0，根據以上分析，可知Xi是支持向量。顯然地，式(5)的形式和SVM 的最優分類函數很一致，確保了最優解的唯一性。

2 基于模糊核聚類粒化的粒度支持向量機

2.1 問題的提出

在研究中發現，只有支持向量才對SVM 的訓練起積極作用，它們是非常重要的，對于SVM 是不可或缺的，而其余的非支持向量對于分類超平面是不起作用的，甚至可能產生負面影響，比如增加了核矩陣的容量，降低了SVM 的效率。GSVM 也存在同樣的問題，只有支持向量粒才對GSVM 的訓練起決定性作用。可以通過理論證明來說明這個觀點的正確性。

定理1粒度支持向量機的訓練過程和訓練結果與非支持向量粒無關。

證明定義Isv={i|al＞0} 和Insv={i|al=0} 分別為支持向量粒和非支持向量粒對應樣本序號的索引集，支持向量粒的個數記為l′。引入只優化支持向量粒對應樣本的問題

要證明定理1，只需要證明式(2)和式(6)同解。用反正法，假設式(6)存在一個最優解a′使得g(a′)＞g(a?) 。由于a?是式(2)的最優解，也即a?是式(6)的可行解，同樣，a′也是式(2)的可行解。由于a?是式(2)的最優解，可得w(a?)＞w(a′)。又因為

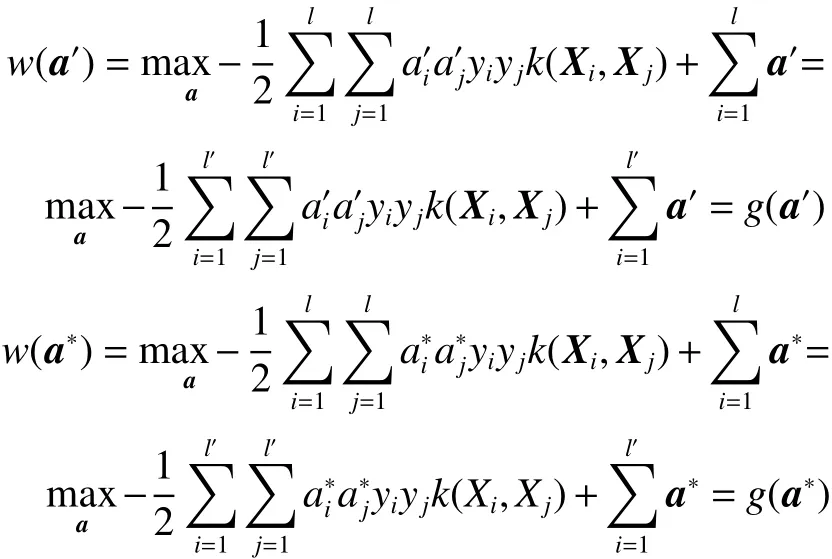
可 得w(a′)=g(a′)＞g(a?)=w(a?) ， 即w(a′)＞w(a?)，這與a?是式(2) 的最優解得出的w(a?)＞w(a′) 相矛盾。定理1 得證。注：a′是l′維向量，代入w的時候拓展為l維向量。

要想迅速地得到支持向量粒，節省粒化的時間，首先了解支持向量的特征，文獻[13]對其特征做了歸納總結。

1)現實中，支持向量一般都是稀疏地聚集在訓練數據集的邊緣。

2)根據第一個特征，則每個類中心附近的數據不會是支持向量，即，離支持向量機超平面較近的數據比較可能是支持向量，這就為支持向量的選取提供了快速的獲取方法。

2.2 問題分析

圖1 中，紅色部分的數據是GSVM 的支持向量粒，它們決定了分類超平面。并且從中可以看出，對于每一類，離類中心越遠的點，就越有可能是支持向量粒。并且，從圖1 中還可以看出，落在每一個環上的樣本，它們離類中心的距離差不多相等。 離類中心越遠的環就越有可能含有多的支持向量粒。基于這個思想，本文先把樣本映射到核空間，按類標簽的個數進行粗粒劃分，確保相同標簽的樣本都在同一個粗粒中。 然后，對于每一個粗粒，采用模糊聚類的方法進行粒化，具有相同隸屬度的樣本歸為一個粒，進行細粒劃分。 每一個細粒就對應圖1 中的一個環，從圖中可以看出，離粗粒中心越遠的環，越靠近分類超平面，其是支持向量粒的可能性越大。而離粗粒中心越遠的環，其隸屬度越小。因此，給定一個閾值，當細粒的隸屬度小于給定的閾值，就說明其處于粗粒的邊緣，是支持向量粒，進而提取出支持向量粒.

圖1 支持向量分布圖Fig.1 The distribution of support vectors

2.3 模糊核聚類

模糊核聚類(fuzzy kernel cluster, FKC)的主要思想是先將數據集映射到高維空間，然后直接在高維空間進行模糊聚類。而一般的聚類算法是直接在原始空間進行聚類劃分。與其他的聚類算法相比，模糊核聚類引入了非線性映射，能夠在更大程度上提取到有用的特征，聚類的效果會更好。

設原空間樣本集為X=(x1,x2,···,xN)，xj∈Rd，j=1,2,···,N。 核非線性映射為?:x→?(x)，在本文中，采用Euclid 距離作為距離測量方法，由此得到模糊核C-均值聚類：

式中：C是事先確定的簇數；m∈(1,∞) 是模糊加權指數，對聚類的模糊程度有重要的調節作用；vi為第i類的類中心； ?(vi) 為該中心在相應核空間中的像。

按模糊C-均值優化方法，隸屬度設計為

且有

為了最小化目標函數，需要計算k(xj,vi) 和k(vi,vi) ，由k(xi,xj)=＜ ?(xi),?(xj)＞ 可得：

把式(9)～(11)代入式(7)，可以求出模糊核C-均值聚類的目標函數值。

模糊核C-均值聚類的算法步驟如下：

1) 初始化參數： ε、m、T和C；

2) 對訓練數據集進行預處理；

3) 設置vi(i=1,2,···,C) 的初始值；

4)計算隸屬度uij(i=1,2,···,C;j=1,2,···,N)；

5) 計算新的k(xj,vi) 和k(vi,vi)， 更新隸屬度uij為

2.4 FKC-GSVM 的算法步驟

目前，已有的粒度支持向量機算法模型大都是直接在原始空間對數據集進行粒化和提取，然后映射到核空間進行SVM 的訓練。然而，不同空間的轉換，很有可能丟失了數據集的有用信息，降低學習器的性能。為了避免因數據在不同空間分布不一致而導致泛化能力不高的問題，本文采用模糊核聚類的方法直接在核空間對數據集進行粒化、提取和SVM 的訓練。基于以上思想，本文提出了基于模糊核聚類粒化的粒度支持向量機(fuzzy kernel cluster granular support vector machine, FKC-GSVM)。FKC-GSVM 算法包括3 部分：采用模糊核聚類進行粒度的劃分；設定閾值，當每個粒子的隸屬度大于規定的閾值時，認為這個粒子為非支持向量粒，丟棄，而剩余的粒子為支持向量粒；在核空間對支持向量粒進行SVM訓練。具體的算法步驟如下：

1) 粗粒劃分：以類標簽個數l為粒子個數，對 訓練樣本進行粗粒的劃分，得到l個粒子；

2) 細粒劃分：采用模糊核聚類分別對l個粒子進行細粒劃分，計算每個粒子的隸屬度；

3) 支持向量粒的提取：給定一個閾值，當一個粒子的隸屬度小于給定的閾值，提取這個粒子(支持向量粒)，提取出來的支持向量粒組成了一個新的訓練集；

4) 支持向量集的訓練：在新的訓練樣本集上進行GSVM 訓練；

5) 泛化能力的測試：利用測試集測試泛化能力。

2.5 FKC-GSVM 算法性能分析

下面，從2 個方面對FKC-GSVM 的算法性能進行分析：

1) FKC-GSVM 的收斂性分析

與SVM 相比，FKC-GSVM 采用核空間代替原始空間進行粒化，提取出支持向量粒后在相同的核空間進行GSVM 訓練，其訓練的核心思想依然是采用支持向量來構造分類超平面，這與標準支持向量機相同。既然標準支持向量機是收斂的，則FKC-GSVM 也是收斂的。但是由于FKCGSVM 剔除了大量對訓練不起積極作用的非支持向量，直接采用支持向量來訓練，所以它的收斂速度要快于標準支持向量機。

2) FKC-GSVM 的泛化能力分析

評價一個學習器性能好壞的重要指標是其是否具有較強的泛化能力。眾所周知，由于SVM采用結構風險最小(SRM)歸納原則，因此，與其他學習機器相比，SVM 的泛化能力是很突出的。同樣，FKC-GSVM 也執行了SRM 歸納原則，并且直接在核空間選取支持向量，確保了數據的一致性，具有更好的泛化性能。

3 實驗結果及分析

3.1 UCI 數據集上的實驗

為了驗證FKC-GSVM 的學習性能，本文在Matlab7.11 的環境下對5 個常用的UCI 數據集進行實驗，這5 個數據集的描述如表1 所示。在實驗中，采用的核函數為高斯核函數，并且采用交叉驗證方法選取懲罰參數C和核參數 σ ， 聚類數c設為20。影響算法表現的主要因素是閾值k的設定，為此，對不同的閾值對算法的影響進行了分析。

數據集 Abalone Contraceptive Method Choice Pen-Based Recognition of Hand-written Digits NDC-10k NDC-1l#訓練集 3 177 1 000 6 280 10 000 100 000#測試集 1 000 473 3 498 1 000 10 000維度 8 9 16 32 32

為了比較數據集在原空間粒化和在核空間粒化的不同效果，本文采用基于模糊聚類的粒度支持向量機(FCM-GSVM)、基于模糊核聚類的粒度支持向量機(FKC-GSVM)和粒度支持向量機(GSVM)等3 種算法對5 個典型的UCI 數據集進行了 測試，測試結果如表2 所示。為了更直觀地看出FKC-GSVM 在不同閾值條件下的分類效果，給出了Contraceptive Method Choice 數據集在不同閾值條件下采用FKC-GSVM 分類的效果圖，如圖2～圖5 所示。

表2 FCM-GSVM 與FKC-GSVM 測試結果比較Table 2 Comparison of test results between FCM-GSVM and FKC-GSVM%

FCM-GSVM 和GSVM 是在原空間進行粒度劃分和支持向量粒的提取，然后把支持向量粒映射到高維空間進行分類，而FKC-GSVM 是直接在核空間進行粒度劃分和支持向量粒的提取，然后在相同的核空間進行分類。從表2 的測試結果可以看出，由于FCM-GSVM 和GSVM 可能導致數據在原空間和核空間分布不一致，在相同的閾值條件下，其分類效果要比FKC-GSVM 的分類效果差，這說明FKC-GSVM 的泛化能力比FCM-GSVM 的泛化能力強。

為了分析在不同閾值條件下FKC-GSVM 的泛化性能，本文給出了0.9、0.85、0.8、0.75 四個不同閾值條件下的實驗。從表2 可以看出，閾值越小，FKC-GSVM 的分類效果越差，這是因為閾值越小，選取的支持向量粒就越少，這一過程可能丟失了一些支持向量，影響了分類效果。但是閾值越小，大大壓縮了訓練樣本集，算法訓練的速度得到了很大的提高。因此，對于大規模樣本來說，只要在能接受的分類效果的范圍內，選取合適的閾值，采用FKC-GSVM 就能快速地得到需要的分類效果。圖2～5 是Contraceptive Method Choice 數據集在不同閾值條件下采用FKC-GSVM 分類的效果圖，從這幾個圖中可以很直觀地看出，FKC-GSVM 的分類效果還是比較令人滿意的。

圖2 FKC-GSVM 在閾值為0.9 條件下的分類效果Fig.2 The classification results of FKC-GSVM under the threshold 0.9

圖3 FKC-GSVM 在閾值為0.85 條件下的分類效果Fig.3 The classification results of FKC-GSVM under the threshold 0.85

圖4 FKC-GSVM 在閾值為0.8 條件下的分類效果Fig.4 The classification results of FKC-GSVM under the threshold 0.8

圖5 FKC-GSVM 在閾值為0.75 條件下的分類效果Fig.5 The classification results of FKC-GSVM under the threshold 0.75

3.2 NDC 大數據集上的實驗

為了測試FKC-GSVM 處理大數據集的性能，在實驗中，采用的數據集是NDC 大數據集[20]，是由David Musicant’s NDC 數據產生器產生的，NDC 數據集的描述如表3 所示。在實驗中，FKCGSVM 的測試結果將與現在比較流行的孿生支持向量機(twin support vector machines, TWSVM)的測試結果[20]從測試精度和運行時間2 方面進行對比。其中，FKC-GSVM 的運行環境、參數設置方法和實驗3.1 一樣，閾值k= 0.9；TWSVM 的懲罰參數和核參數的選取都是從 {2-8,2-7,···,27} 這個范圍內采用網格搜索算法進行選擇。表4 顯示的是FKC-GSVM 和TWSVM 兩種算法的運行結果。

表3 實驗采用的NDC 數據集Table 3 NDC datasets used in experiments

表4 2 種算法對NDC 數據集的測試結果Table 4 Comparison of two algorithms on NDC datasets

從表3 中可以看出，本實驗測試的對象為5 種數據集，NDC-3L 的訓練樣本數為300 000 個，而NDC-1m 的樣本增加到了1 000 000 個，同樣，測試樣本也從30 000 增加到了100 000，特征數都是32 維。這3 個數據集主要是為了測試算法在處理維度一樣而數據量不斷增加時候的學習性能。為了進一步測試學習算法處理高維樣本的性能，NDC1 和NDC2 這2 個數據集的維數分別是100 和1 000，設置他們的訓練樣本量和測試樣本量都一樣，都是5 000。

實驗結果如表4 所示，從中可以看出，當數據集為NDC-1m 時，由于訓練時間過高，采用TWSVM 算法無法將實驗進行下去。然而，FKC-GSVM 在處理NDC-1m 數據集時能夠在合理的運行時間內得到較滿意的精度解，這表明了FKC-GSVM 在處理大數據時是具有優勢的。同樣，在處理NDC1 和NDC2 這2 個高維數據集時，從表4可以明顯看出，FKC-GSVM 處理高維數據的效果也是不錯的。實驗結果充分說明了FKC-GSVM 的學習能力比TWSVM 的強，更適合于處理大數據集。

4 結束語

GSVM 是將訓練樣本在原空間粒化后再映射到核空間，這將導致數據與原空間的分布不一致，從而降低了GSVM 的泛化能力。為了解決這個問題，本文提出了一種基于模糊核聚類粒化的粒度支持向量機方法(FKC-GSVM)。FKC-GSVM 通過利用模糊核聚類直接在核空間對數據進行粒的劃分和支持向量粒的選取，然后在相同的核空間中進行支持向量粒的GSVM 訓練，在標準數據集的實驗說明了FKC-GSVM 算法的有效性。但是閾值參數的選取仍具有一定的隨意性，影響了FKC-GSVM 的性能。如何自適應地調整合適的閾值，將是下一步要研究的工作內容。