圖像情境下的數字序列邏輯學習

梁慧，曹峰，錢宇華，郭倩，梁新彥

（1.山西大學 大數據科學與產業研究院，山西 太原 030006; 2.山西大學 計算智能與中文信息處理教育部重點實驗室，山西 太原 030006; 3.山西大學 計算機與信息技術學院，山西 太原 030006）

數字序列邏輯學習的發展可以說是經歷了漫長的歲月，其可以追溯到人類早期歷史。例如，古時滿月的預測[1]，并且其仍然是當今研究的活躍領域，在股市中，我們經常會聽到有神奇數字時間之窗這一說法，其用到的波浪理論的數字基礎就是一系列的數列，此數列稱為fibonacci 序列。大自然中還有很多與fibonacci 序列有關的奇妙現象，如蜘蛛網、水流的旋渦、蝸牛殼的螺紋以及星系內星球的分布等。

數字序列邏輯學習問題是歸納推理和模式發現的經典問題之一[2-3]，這些問題在哲學和數學領域中已經研究了數千年，在心理學和計算機科學領域中也已經研究了數十年[4]。近些年來隨著機器學習和深度學習的不斷發展[5-8]，序列預測問題更是吸引了大家的廣泛研究。數字序列預測問題在各個領域的應用也是相當的廣泛。其可以編碼漸進矩陣問題[9]，該問題是用二維矩陣表示的，科學預測問題包括股票的預測、智商測試等，以及許多歸納推理問題[10-12]。早在1963 年，Simon等[13]就提出了針對一系列字母序列來預測的模式描述程序，并解釋了人類如何從記憶中的概念或規則產生連續模式。Sanghi 等[14]提出了一種用于智力測試的程序，該程序還解決了各種數字序列預測問題。且針對數字序列預測問題的解決已有很多方法，例如：反統一算法成功應用于交替序列和斐波納契序列。Siebers 等[15]提出了一種半分析方法用以解決自然數序列歸納問題，這實則是一種典型的智力測試任務，該方法通過術語結構的啟發式枚舉來猜測給定數字序列的術語結構，最后利用數字序列評估系統來評估該方法，最終結果精度達到93.2%。然而，其缺點是枚舉和搜索受到一種看似合理的偏見的嚴格限制。Strannegard 等[16]提出了IQ 測試中數字序列預測問題的計算方法。該計算方法是通過開發ASolver 來實現的，ASolver 是一種基于有限工作記憶思想的擬人化認知系統，其利用了人類推理的模型。結果表明，該算法的性能優于Maple 和Wolfram-Alpha 等數學工具。Hofmann 等[17]證明了歸納程序系統IGOR2 可以解決數字序列預測問題，其不同于上述專門用于解決數字序列域中問題的系統，IGOR2 可以解決不同問題解決域中的問題。IGOR2 是一個從小組輸入/輸出示例中學習功能程序的系統。但不足之處在于其無法很好地處理負數和交替序列。Ragni 等[18-19]提出了一種基于人工神經網絡(ANNs)的動態學習方法來解決數字序列的預測問題。其總體結果與人類水平相當，但誤差分布差異很大，且無法解決Nested 序列問題(見2.1)。

上述方法都是傳統的方法，它是基于已知的數字和規則來構建模式，然后預測數字。然而，傳統數字序列邏輯學習也存在一定的不足，它很難解決未知數字和規則的模式構建的數字序列預測問題。例如，每月的天數序列、Nested 序列、交替序列、帶負數的序列等。舉一個更為具體的例子： 1 )2,4,6,8,10,12,···, 2)1,2,3,5,4,4,2,···, 對于第1 個序列，可以明顯地觀察到其是一個加2 的規律，這樣就可以構建一個滿足該規律的模式，傳統數字序列技術可以很容易地解決此類預測問題。對于第2 個序列，難以看出其中的規律，且很難用傳統方法得到一種滿足此序列的模式來預測該序列，實際上該序列是書寫漢字如一二三四等需要的筆畫數，故而下一個預測結果應為2。

針對傳統數字序列邏輯學習的不足，本文提出了圖像數字序列邏輯學習任務，以從另一個角度來解決數字序列預測問題，其可以很好地解決傳統數字序列難以解決的未知數字和規則的模式構建的序列預測問題。在傳統數字序列邏輯學習中，數字的含義及其規則都已被事先定義。而本文提出的圖像數字序列邏輯學習是在不知道圖像間關系和圖像內包含的內容的意義的前提下，仍可以自動學習出其包含的內在邏輯模式。在本文中，圖像序列中的所有圖像都是15×85 像素的黑白圖像，且每張圖像包含一個多位數。然后將圖像傳遞給計算機，且并不告訴計算機圖像中包含的內容是什么，讓計算機自動學習圖像之間的內在邏輯模式，并且預測下一張圖像中的內容。由此看來，圖像數字序列邏輯學習不僅可以解決數字序列預測問題，更是為解決一系列未知邏輯模式構建任務提供了一種可能。

1 研究方法

本節主要介紹了圖像數字序列邏輯學習的基本任務，并詳細描述了4 種有代表性的深度神經網絡的網絡結構(MLP、LSTM、CNN_MLP、ResNet)。

1.1 基本任務

圖像數字序列邏輯學習是從另一個角度來解決數字序列預測問題，其與傳統數字序列解決方案不同。傳統數字序列技術是在已知數字和規則的前提下構建模式。而本文的方法是在不知道圖像間關系和圖像內包含的內容的意義下來預測序列，然后利用深度神經網絡來完成數字序列邏輯學習任務，該任務的輸入是幾張相關的圖像序列，其輸出仍然是圖像，展示的是下一張圖像序列預測的結果。

首先將圖像序列傳送給計算機，讓計算機在不知道圖像間關系和圖像內包含的內容的意義的前提下自動學習出其內在邏輯模式，從而進行數字序列的預測。所有這些圖像都是黑白圖像，右對齊，大小歸一化(15×85)，每張圖像包含一個多位數，其可以是正數或負數，每張圖像中的最大位數設置為10。如圖1 所示，其中圖1(a)的位數設置為9 位，圖1(b)位數設置為10 位，圖1(c)位數設置為11 位，原本數字為32 282 246 720，由于超出位數的設定，圖像中最左位的數字無法完全顯示，圖1(d)為負數情形，位數設置為10 位(除符號位)。然后本文使用幾種代表性的深度神經網絡來完成數字序列邏輯學習任務，并加以比較分析。給出網絡結構的詳細描述。最后，為了測試本文的網絡性能，本文以某種邏輯關系隨機生成一批測試樣本，每個樣本包括k張圖像，將前k?1 張圖像傳入模型中，測試生成的圖像是否正確。

圖1 圖像展示Fig.1 Image display

1.2 網絡結構

本文在構造的數據集上比較了幾種有代表性的深度神經網絡的性能(MLP、LSTM、CNN_MLP、ResNet)。數據集的構造詳見2.1。全部模型均使用均方誤差(MSE) 損失作為優化函數，ADAM[20]作為優化器，衰減率參數設置為β1=0.9，β2=0.999。每個網絡的詳細結構和超參數設置如圖2。

圖2 4 種神經網絡結構Fig.2 Four neural network structures.

多層感知機(MLP) 在本文中，使用一個4 層的多層感知機網絡來構建模型，該模型包含輸入層、隱藏層和輸出層。采用一個3 層架構的隱藏層，每個隱藏層將線性整流函數(ReLU)[21]作為激活函數。使用Sigmoid 函數作為網絡的輸出層。網絡結構如圖2(a)所示。

長短期記憶網絡(LSTM) 本文采用標準的LSTM 網絡結構，它是一種特殊的RNN，主要是為了解決長序列訓練過程中的梯度消失等問題[22]。而且由于LSTM 是按順序地接收輸入數據，這非常適合于本文的序列預測問題。本文將圖像特征向 量?(xi) 按 順 序 地 傳 入LSTM 中 以 編 碼 隱 藏 狀態hi， 其輸出ht依賴于以前的狀態ht-1，當前的觀察?(xt) 以及上一時刻的單元狀態ct-1。其單元狀態和隱藏狀態公式如下：

式中：ct是t時刻的單元狀態；f、i和o分別表示遺忘門、輸入門和輸出門；表示當前輸入的單元狀態。結構如圖2(b)所示。

卷積-全連接神經網絡(CNN-MLP)本文使用一個標準的4層卷積神經網絡[23-24]，并將ReLU非線性函數作為卷積層的激活函數，在卷積輸出層后連接一個2層的全連接層(MLP)。為防止過擬合在第一個全連接層上使用丟失率為0.5 的dropout[25]技術。結構及其超參數設置如圖2(c)所示。

深度殘差網絡(ResNet)深度殘差網絡有很多不同的結構[26]，包括ResNet18、34、50、101、152 等，在本文實驗中，這幾種網絡的實驗效果相差無幾，所以在這里僅展示了ResNet18 的實驗結果。其結構如圖2(d)所示。

本文的具體步驟如下：在訓練階段，傳遞給計算機N張圖像，每張圖像包含一個多位數，如圖3所示(假設N=4)，而且并不告知計算機每張圖像中包含的內容是什么，然后使用以上所提及的深度神經網絡來完成數字序列邏輯學習任務，以便計算機可以從前3 張圖像間的邏輯模式自動學習第4 張圖像。在測試階段，以某種邏輯關系隨機生成一批測試樣本，每個樣本包括4 張圖像，將前3 張圖像放入模型中，以查看是否可以生成正確的預測圖像。

圖3 計算機不知道給定圖像中所包含的內容是什么Fig.3 The computer doesn't know what the content in the given image is

對于數據分析，本文系統地改變學習速率、批量大小、隱藏節點的數量和訓練迭代等。這些變化應該允許將不同的神經網絡模型與經驗結果進行比較。此外，本文將在所構造的數據集上對比分析不同的深度神經網絡模型的性能，進一步驗證本文所提出的圖像數字序列邏輯學習對未知數字和規則的模式構建的序列預測的有效性。

2 實驗及分析

本節詳細介紹了圖像序列數據集的構造過程及原則，并在所構造數據集上利用深度神經網絡對各維度的圖像數字序列的預測加以分析比較。

2.1 數據集

正如本文前面所提及，圖像數字序列預測問題的解決方法與傳統數字序列的解決方法不同，它從另一種角度來解決數字序列預測問題。傳統數字序列是在已知數字的意義下，然后根據序列背景知識、結構復雜性等進行模式的構建，從而求解數字序列，而本文的方法是計算機在不知道如圖3 所示的a、b、c、d以及A、B、C、D間關系的前提下自動地學習出其中所包含的內在邏輯模式，進而預測出所要求解的圖像。

本文構造了4 個大的數據集，其包含各種圖像序列，在本文中，根據其解決方案的不同將數據集分為4 種不同的類型，分別為：Linear、Multiplication、Fio 和Nested。各類型圖像序列的詳細描述如下：1)Linear 序列下一張圖像的生成僅與前一張圖像內容相關聯，與其他項內容無關，其僅涉及“+”和“?”兩種數學運算，例如等差序列就是Linear 序列的一個特例；2)Multiplication 序列僅包含“×”運算符，并且其每張圖像的生成原理與Linear 序列的生成原理相同，即僅與前一張圖像內容相關；3)Fio 序列不僅與前一張圖像的內容相關聯，而且與前2 張圖像的內容相關聯，所涉及的運算符包括“+”和“?”。例如Fibonacci 序列就是Fio 序列的一個特例；4)對于Nested 序列而言，其包含更多的操作運算符：“+”、“?”和“×”，并且其運算不僅僅與前2 項相關，還與任意的隨機常數項相關聯。用數學公式可以表述為：

式中：f(n) 表示當前圖像；f(n-1) 表示前一張圖像。式 (3) ～ (4) 均是Nested 序列的數學表述。從另一層面來講，它可以說是Multiplication 序列、Linear 序列和Fio 序列的復雜混合序列。

本文整個數據集的構造原則：1)為方便構造數據集，本文只考慮整數圖像序列，圖像序列可以包含正數或負數；2)每張圖像都包含一個多位數，且每張圖像中的最大位數設置為10。所有這些圖像均是黑白圖像，對齊和尺寸標準化(15×85)；3)每張圖像位數的設置最大為10 位，本文選擇的數據集僅是一個小樣本集，其在總集(即我們數據的變動范圍[?999 999 999 9, 999 999 999])中的占比很小，也就是說，本文確保訓練集、測試集互不相交。本文為每種類型的數據集均選擇了60 000 的圖像數字序列，其中50 000 用于訓練，10 000 用于測試。Linear 序列、Multiplication 序列、Fio 序列和Nested 序列的部分數據集如圖4～7 所示(以4 維的圖像數字序列為例)。

圖4 Linear 序列Fig.4 Linear sequences

圖5 Multiplication 序列Fig.5 Multiplication sequences

圖6 Fio 序列Fig.6 Fio sequences

圖7 Nested 序列Fig.7 Nested sequences

2.2 實驗結果及分析

到目前為止，解決數字序列預測的方法幾乎都是在基于給定數字的含義下，通過歸納序列的潛在規律，構建出滿足該數字序列規律的模式，從而預測數字。而且，對于傳統數字序列而言，其模式的長度與最終的預測結果有很大的關系，即輸入節點的數量對最終預測結果的準確率有極大的影響。Ragni 等[18]提出了一種基于人工神經網絡的動態學習方法來解決數字序列預測問題，該實驗結果表明：輸入節點的最佳配置為4 個節點。因此，本文對輸入維度，即輸入的圖像數進行了實驗并加以分析比較。

本文對已構建的4 個數據集進行了維度上的擴展，分別擴展為4 維圖像序列、5 維圖像序列和6 維圖像序列，這里并沒有擴展3 維圖像序列，因為它的不確定性太大，例如本文的Fio 序列，其并非簡單地與最后一個數字有關，而是與最后2 個數字相關聯。關于數據集及其分類部分在3.1 節中已有詳細介紹，此處將不再贅述。

對于實驗1，首先給定計算機4 張圖像，與此同時并不告知計算機每張圖像中包含的內容是什么，在學習過程中，本文利用4 種代表性的深度神經網絡(MLP、LSTM、CNN_MLP、ResNet)來完成數字序列邏輯學習任務，以便計算機可以從前3 張圖像間的邏輯模式自動學習出第4 張圖像。在測試階段，本文任意輸入4 維圖像序列，并將前3 張圖像放入模型中進行測試，使用OCR 工具[27]來識別得到的預測圖像，將OCR 的結果與期望輸出進行比較，并計算預測正確的百分比。

對于實驗2，其步驟與實驗1 幾乎相同。區別之處在于：在學習階段，本文給計算機提供5 張圖像，讓計算機自動學習每張圖像間的內在邏輯模式。在測試階段，輸入5 維圖像序列，并將前4 張圖像傳遞到模型中以預測結果的正確性。

對于實驗3，步驟與前2 個實驗幾乎相同。不同的是，在學習階段，本文給計算機提供6 張圖像，讓計算機自動學習出每張圖像間的邏輯模式。在測試階段，本文輸入6 維圖像序列，并將前5 張圖像傳入模型進行測試，以檢測本文是否可以生成具有正確結果的圖像。

本文利用上述提及的4 種深度神經網絡模型對每個實驗進行了準確度的測試，實驗結果如表1所示，從表1 可以看到4 種神經網絡模型可以很好地預測Linear 序列和Fio 序列，且維度越高，預測準確率越高。對Multiplication 序列和Nested 序列而言，MLP 模型和LSTM 模型對這2 種序列的預測均呈現一種維度越高準確率越低的趨勢。相反，CNN_MLP 模型和ResNet 模型呈現一種維度越高，預測的準確率越高的情形，且ResNet 模型對于這2 種序列的預測結果總體而言要優于其他的模型。

表1 4 種神經網絡模型在本文數據集上的實驗結果Table 1 Experimental results on the our own dataset for the four neural network models

本文對4 種深度神經網絡模型在4 維、5 維和6 維圖像序列的性能比較見圖8～10。從各個維度圖像序列的折線圖中可以明顯觀察到，4 種模型可以很好地預測Linear 序列和Fio 序列的結果，無論它們是4 維、5 維還是6 維圖像序列，且維度越高，準確率越高。這可能是由于Linear 序列和Fio 序列自身規律較為簡單，例如，給定Linear 圖像序列5、7、9，預測結果11，計算機可以很明顯知道是一個加2 的規律，進而可以很容易地學到內在邏輯模式，從而進行序列的預測。

4 種深度神經網絡模型在4 維圖像序列的性能比較見圖8，LSTM 對Multiplication 序列的預測準確率明顯高于其它模型，但當維度升高時，如圖9～10 所示，可以看到LSTM 模型對該序列的預測下降了，而ResNet 和CNN_MLP 模型對于該序列的預測效果呈現越來越好的趨勢，這可能是由于ResNet 和CNN_MLP 網絡模型較為復雜，當維度越高其獲得的信息就會越多，越是可以較為準確的學到該圖像序列的邏輯模式。而LSTM 模型可能由于維度越高，其更易受到其子序列的影響。例如6 維圖像序列：1、2、4、8、16，預測32，該圖像序列中包含子序列1、4、16 和2、8 等。在LSTM 模型中其極易受到子序列的影響，從而致使預測結果有誤，如子序列1、4、16，其是一個乘4 的規律，有可能下一個數預測為64，而當只給定4 維圖像序列時，如2、4、8，預測結果16，其反而較易進行該序列的預測。

圖8 4 種深度神經網絡模型在4 維圖像序列中的性能比較Fig.8 A comparison on performance of four kinds of deep neural network models in 4-dimensional image sequences

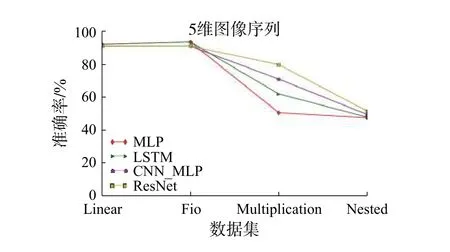
圖9 4 種深度神經網絡模型在5 維圖像序列中的性能比較Fig.9 A comparison on performance of four kinds of deep neural network models in 5-dimensional image sequences

圖10 4 種深度神經網絡模型在6 維圖像序列中的性能比較Fig.10 A comparison on performance of four kinds of deep neural network models in 6-dimensional image sequences

對4 維和5 維圖像序列的性能比較見圖8～9，各模型對于Nested 序列的預測均集中在一定的范圍，這可能是由于Nested 序列較為復雜，所有模型在該序列上的性能沒有太大區別，但隨著維度增高，從圖10 可以發現ResNet 和CNN_MLP 模型對于該序列的預測稍有提升，而MLP和LSTM 模型對于此序列的預測又有所下降，這可能是由于MLP 和LSTM 模型較為簡單，而Res-Net 和CNN_MLP 模型較為復雜，對于這種復雜序列，隨著維數增高，復雜模型在圖像序列的預測上其準確率極有可能上升，而簡單模型的準確率極易下降。

此外，本文分析比較4 種深度神經網絡模型在Linear 序列、Fio 序列、Multiplication 序列和Nested 序列上的性能，如圖11～14。從圖11可以發現：隨著維數的增高，各模型對于Linear 序列預測的準確率提升并不明顯，這可能是與Linear 序列自身的規律有關，其規則是僅與前一項內容相關聯，而與其他項無關，所以當維數增高時，計算機所獲得的序列的內在邏輯模式的信息實則是沒有太大的變化，例如，給定序列2、3、4，預測結果5，計算機可以很明顯知道其是一個加1 的規律，當再給定序列1、2、3、4 預測下一個內容時，計算機并沒有從中得到更多的信息，故而維度雖然增高了，但其準確率的變化并沒有很大改變。

圖11 4 種深度神經網絡模型在Linear 序列上的性能比較Fig.11 A comparison on performance of four kinds of deep neural network models in Linear sequences

圖12 4 種深度神經網絡模型在Fio 序列上的性能比較Fig.12 A comparison on performance of four kinds of deep neural network models in Fio sequences

圖13 4 種深度神經網絡模型在Multiplication 序列上的性能比較Fig.13 A comparison on performance of four kinds of deep neural network models in Multiplication sequences

圖14 4 種深度神經網絡模型在Nested 序列上的性能比較Fig.14 A comparison on performance of four kinds of deep neural network models in Nested sequences

對比圖12 的Fio 序列，其規則是不僅僅與前一項內容相關聯，而且與前兩項的內容相關，這就使得當維數越高，即給定的圖像數越多，計算機得到的圖像間的信息就會越多，就越易預測該序列，可以很明顯地看到圖12 中準確率的提升隨著維數的增高越來越明顯。

Multiplication 序列和Nested 序列的性能比較見圖13～14，從圖中可以看出維度越高，對于CNN_MLP 和ResNet 模型而言預測的準確率越高。相反，MLP 和LSTM 模型對于這2 種序列的預測均呈現一種維度越高準確率越低的趨勢。這可能是由于CNN_MLP 和ResNet 模型自身較為復雜，其對于這種復雜序列來說，其預測精度反而是易于隨著維數增高而增大。而對于MLP 和LSTM 模型而言，其模型自身較為簡單，加之Multiplication 序列和Nested 序列又較為復雜，相當于是個模型簡單任務難的問題，其對于此序列的預測難度就會加大，容易導致維度越高準確率越低的情況。

2.3 結果分析

本小節從視覺效果的角度展示了每種類型圖像序列在不同維度上的實驗結果，如圖15～17所示(其中包括正確的預測和錯誤的預測)。

圖15 4 維圖像序列Fig.15 4-dimensional image sequences

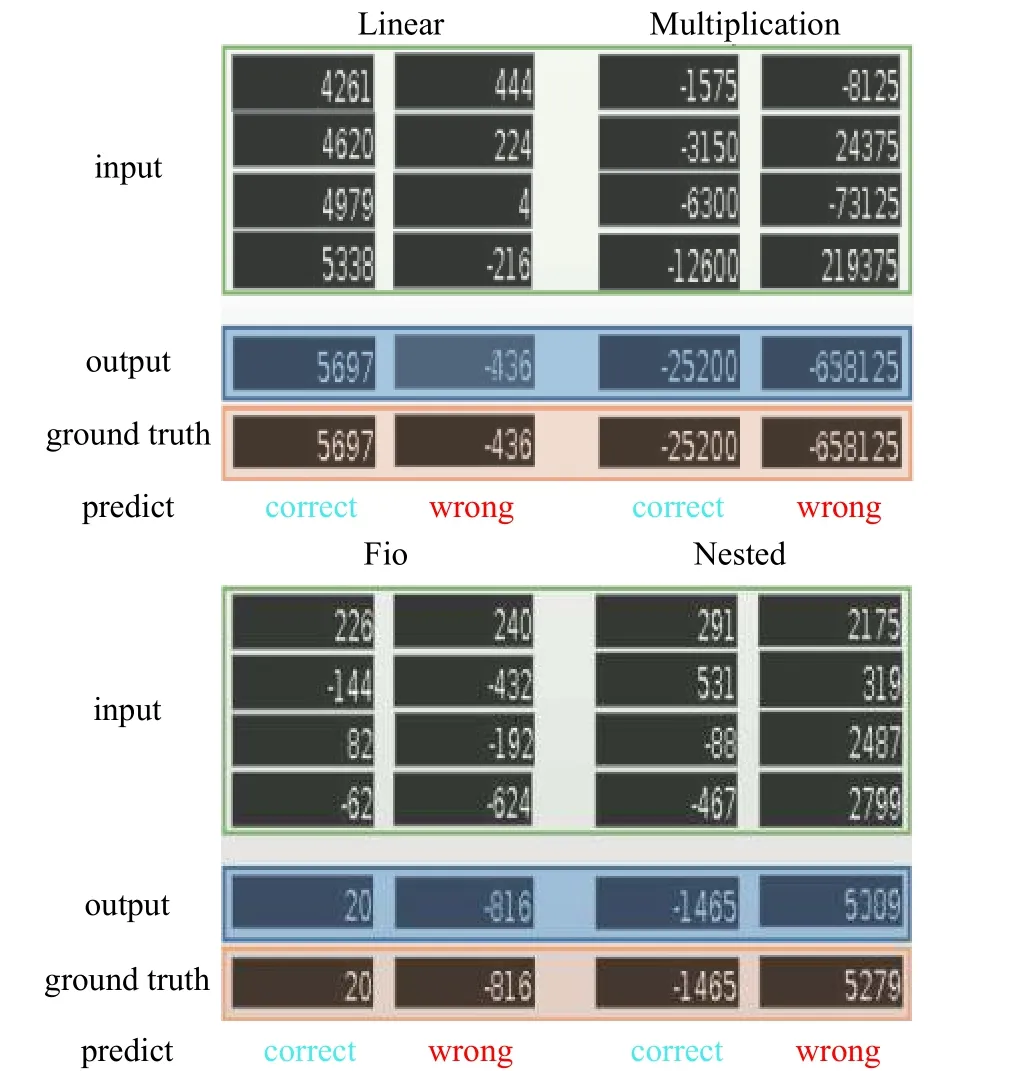
圖16 5 維圖像序列Fig.16 5-dimensional image sequences

本文僅展示了4 維、5 維、6 維圖像序列的部分實驗結果。從這些實驗結果發現預測誤差的原因可能如下：1) 當輸出圖像模糊時，很容易引起OCR 工具識別錯誤，例如圖15 中的Fio 序列，觀察錯誤的那一欄，當輸出圖像模糊時，圖像中輸出結果的第2 位(從右往左)有可能是6 或8，這就極易導致OCR 的識別出錯，再如，圖15～16中的Multiplication 序列，圖16 中的Linear 序列和Fio 序列等。2) 其對負號的圖像預測有時是不準確的，例如圖17 中的Multiplication 序列和Nested 序列等。3) 結果輸出中的位數越大，其預測出錯的可能性就會越大，因為計算位數越大，相對而言，其難度就會越大，預測錯誤的可能性就會加大。

圖17 6 維圖像序列Fig.17 6-dimensional image sequences

3 結束語

數字序列邏輯學習任務一直以來都是人工智能的一個研究熱點。而且未知的數字和規則的模型構建數字序列問題的預測始終是一個具有挑戰性的任務。傳統的數字序列技術是基于已知數字的含義下，并根據序列本身的規律特征構造滿足該規律的模式，以便進行數字序列的預測。本文的方法是在不知道圖像間關系和圖像內包含的內容的意義的情況下利用深度學習的方法完成數字序列邏輯學習任務來預測下一張圖像內容。同時，人類對于這種未知的數字和規則的模型構建的數字序列極易限制其中，無法快速計算出結果甚至無法得到正確結果。而本文所提出的方法為解決此類序列問題提供了一種可能。

在未來的工作中，我們將進一步探索如何提高精度及對缺失數據的預測，同時期望可以對任意位置的圖像內容進行預測，而非單一地對下一張的圖像內容進行預測，特別地，下一步希望可以提出更適用于數字預測邏輯學習任務的模型以求精度上面的突破。

參考文獻：：

[1]BOGOSHI J.The oldest mathematical artefact[J].The mathematical gazette, 1987, 71(458): 294-294.

[2]SCHMID U, KITZELMANN E.Inductive rule learning on the knowledge level[J].Cognitive systems research, 2011,12(3/4): 237-248.

[4]COLTON S, BUNDY A, WALSH T.Automatic Invention of Integer Sequences[M]// The fertility of the soil /.Cambridge University Press AAAI/IAAI, 2000: 558-563.

[5]QIAN Y, LI F J, LIANG J Y, et al.Space structure and clustering of categorical data[J].IEEE transactions on neural networks and learning systems, 2016, 27(10):2047-2059.

[6]QIAN Y, XU H, LIANG J Y, et al.Fusing monotonic decision trees[J].IEEE transactions on knowledge and data engineering, 2015, 27(10): 2717-2728.

[7]QIAN Y, LI Y, LIANG J, et al.Fuzzy granular structure distance[J].IEEE transactions on fuzzy systems, 2015,23(6): 2245-2259.

[8]QIAN Y, LIANG J, PEDRYCZ W, et al.Positive approximation: An accelerator for attribute reduction in rough set theory[J].Artificial intelligence, 2010, 174(9/10):597-618.

[9]RAVEN J, et al.Raven progressive matrices[M].Handbook of Nonverbal Assessment, 2003, 223-237.

[10]MUGGLETON S, CHEN J.Guest editorial: special issue on inductive logic programming (ILP 2011)[J].Machine learning, 2012, 89(3): 213-214.

[11]HOLZMAN T G, PELLIGRINO J W, GLASER R.Cognitive dimensions of numerical rule induction[J].Journal of educational psychology, 1982, 74(3): 360-373.

[12]STERNBERG R.J.Handbook of Intelligence[M].Cambridge University Press, 2000.

1） 城鄉規劃學走向計量化的過程中，以計算的基礎為數據，而在大數據時代，該學科具有海量的數據，可在數據分析和數據挖掘等技術的配合作用下，提升城鄉規劃計量水平，并實現對數據資源的高效利用[1]；

[13]SIMON H A, KOTOVSKY K.Human acquisition of concepts for sequential patterns[J].Psychological review,1963, 70(6): 534-546.

[14]SANGHI P, DOWE D.L, A computer program capable of passing I.Q.tests[C]//4th Int.Conf.on Cognitive Science(ICCS'03), Sydney, 2003: 570?575.

[15]SIEBERS M, SCHMID U.Semi-analytic natural number series induction[J].Advances in artificial intelligence,2012, 7526: 249-252.

[16]STRANNEGARD C, AMIRGHASEMI M, ULFSBACKER S.An anthropomorphic method for number sequence problems[J].Cognitive systems research, 2013, 22-23:27-34.

[17]HOFMANN J, KITZELMANN E, SCHMID U.Applying inductive program synthesis to induction of number series a case study with IGOR2[J].Joint german/austrian conference on artificial intelligence(Künstliche Intelligenz).Springer, Cham, 2014: 25-36.

[18]RAGNI M, KLEIN A.Predicting numbers: An AI approach to solving number series[C]// German Conference on Advances in Artificial Intelligence.Springer, Berlin,Heidelberg, 2011:255?259.

[19]RAGNI M, KLEIN A.Solving number series - architectural properties of successful artificial neural networks[C]// NCTA 2011- Proceedings of the International Conference on Neural Computation Theory and Applications, 2011: 224-229.

[20]KINGMA D P, BA J.Adam: A method for stochastic optimization.[C]//Proceedings of the 3rd International Comference on Learning Representations, San Diego, arXiv prerint arXiv: 1412.6980, 2014.

[21]LECUN Y, BENGIO Y, Hinton G.Deep learning[M].Nature, 2015, 521(7553):436.

[22]HOCHREITER S, SCHMIDHUBER, JüRGEN.Long short-term memory[J].Neural computation, 1997, 9(8):1735-1780.

[23]CHUMERIN N.Convolutional neural network[J].Neurocomputing, 2015, 148: 136-142.

[24]KRIZHEVSKY A, SUTSKEVER I, HINTON G E.Imagenet classification with deep convolutional neural networks[J].In: advances in neural information processing systems, 2012: 1097-1105.

[25]SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al.Dropout: a simple way to prevent neural networks from overfitting[J].Journal of machine learning research, 2014,15(1): 1929-1958.

[26]HE K, ZHANG X, REN S, et al.Deep residual learning for image recognition[J].In proceedings of the IEEE conference on computer vision and pattern recognition, 2016:770-778.

[27]SMITH R.An overview of the tesseract OCR engine[C]//icdar.IEEE Computer Society, 2007, 2: 629-633.