基于多層編碼遺傳算法的艦艇改造任務分配方法?

李一夫 宋貴寶 賈汝娜 張文鵬

（1.海軍航空大學 煙臺 264001）（2.國防大學聯合勤務學院研究生管理大隊 北京 100039）

1 引言

由于我國海域范圍遼闊且近年來海洋維權執法任務繁重，提高我國海監漁政執法力量對有效管理海洋秩序、合理利用海洋資源、堅定維護海洋權益等方面具有現實意義。海軍艦艇退役以后，拆卸軍艦的重型武器系統、改裝新設備并移交海洋執法部門一直都是世界各國的慣例。本文將多層編碼的遺傳算法作為工具，尋找最短時間改造退役軍艦的任務分配方案，可以在兼顧執法船只整體噸位、續航能力、功能等有效執法能力的同時，及時緩解執行海洋維權船只不足的問題，最大限度地再利用退役軍艦的剩余價值。

2 問題描述

對退役軍艦的改造問題根本上是根據任務要求合理分配改造工序和船塢，從而提高改造作業過程效率的項目管理問題［1］。從數學的角度可以描述為：有n艘待改造的艦艇要在m個性能不同的船塢內進行改造，每艘艦艇需要經歷q道工序，每艘艦艇的各工序可在不同船塢內完成改造，最終尋求最短時間內全部艦艇完成全部工序改造的優化方案。此外，改造過程中還應滿足以下假設：

1）同一時刻每個船塢只能進行一艘艦艇一道工序的改造；

2）每道工序只能在同一個船塢內完成且中途不可停工；

3）工序存在優先級，但待改造艦艇和船塢無優先級［2～5］。

3 確定工序優先級

改造任務從系統工程的角度出發，工序存在排序問題。由于不同工序間相互關聯，改造先后順序直接影響改造流程的正常運行，例如在加裝新設備之前應先拆除原軍用設備、重設電氣系統等。從系統化、層次化的角度出發，運用定性與定量相結合的方法——層次分析法［1］確定合理的工序優先級可以較好體現項目管理的系統屬性。

4 模型建立

4.1 模型參數

1）待改造艦艇集 P=｛p1，p2，p3，…，pi，…，pn｝，pi表示第i艘待改造艦艇，i=1，2，3，…，n。

2）船塢集 M=｛m1，m2，m3，…，ms，…，mm｝，mj表示第j個船塢，j=1，2，3，…，m。

3）工序序列集 OP=｛op1，op2，op3，…，opq｝。

4）可選船塢 OPM=｛opi1，opi2，opi3，…，opik｝，opij=｛opij1，opij2，opij3，…，opijk｝表示艦艇 pi的工序 j可以選擇的加工機器。

5）改造艦艇的時間矩陣T，tij∈T，表示第i艘艦艇pi改造第j道工序的時間。

6）Aij為第 i艘艦艇開始第 j道工序的時刻，Eij為第i艘艦艇完成第j道工序的時刻。

7）工序間等待時間之和為λ。

4.2 優化模型

工序確定。運用層次分析法確定各工序的優先級，并按優先級由大至小的順序分別對應工序集OP中第一至最后一個元素，即op1優先級最高，op2次之，opq優先級最低。

目標函數。本文目標是使加工所有艦艇所有工序的時間與工序間等待時間λ之和最小。

約束條件。同一時刻一艘艦艇只能在一個船塢內進行改造；同一時刻一個船塢只能改造一艘艦艇；且后一道工序必須在前一道工序完成后才可進行。因此得到如下數學模型：

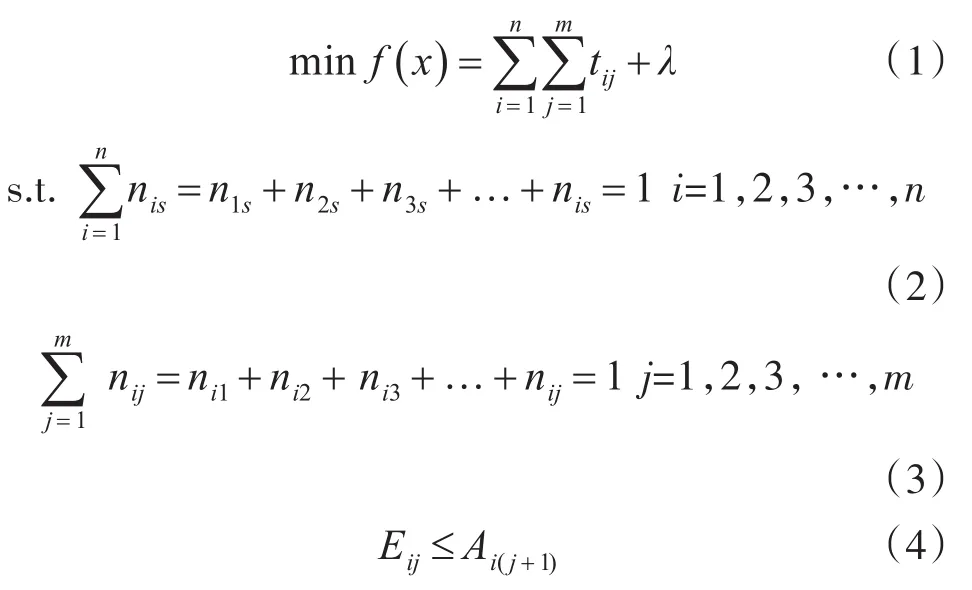
其中，nis表示某時刻s船塢內第i艘艦艇的數量；nij表示某時刻i艦艇在第j個船塢內的數量；Eij表示第i艘艦艇完成第 j道工序的結束時刻；Ai（j+1）表示第 i艘艦艇開始第（j+1）道工序的開始時刻；自變量x為優化后的任務分配方案并最終可形成任務安排甘特圖，從而方便使用。

5 基于多層編碼遺傳算法求解過程及實現

5.1 算法流程

首先進行種群初始化，確定初始解集，按整數編碼的方式對染色體進行多層編碼，；計算適應度值；利用輪盤賭方法對個體尋優；利用整數交叉法產生新的個體；利用整數變異法得到變異后的優秀個體；進行判別選擇循環或者結束［6］。

5.2 算法實現

1）個體編碼

每個染色體按照整數編碼的方式反映一個可行解的二維特征，即工序和所選機器型號。待改造的艦艇總數為n，艦艇ni改造工序為mj時，則每個染色體的長度為

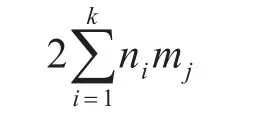
其中染色體的前半部分表示為所有艦艇的改造順序，后半部分表示為艦艇每道工序選擇的船塢序號。例如個體｛16543321//29885321｝“//”前后各有2個數組，各位置一一對應。“//”前面的數表示所有艦艇的改造順序，“//”后面的數表示艦艇的每道工序被處理的船塢序號。第一層編碼描述的改造順序為艦艇1→艦艇6→艦艇5→艦艇4→艦艇3→艦艇3→艦艇2→艦艇1；第二層編碼描述的船塢依次為船塢2→船塢9→船塢8→船塢8→船塢5→船塢3→船塢2→船塢1。

2）計算適應度

染色體的適應度為全部艦艇改造完成的總時間，公式為

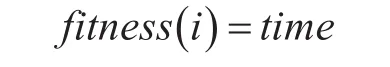
其中time指全部改造任務完成時間，time越小該染色體越優秀［7～8］。

3）選擇操作

采用輪盤賭法選擇適應度較好（適應度值大）的染色體［4］，個體選擇概率為

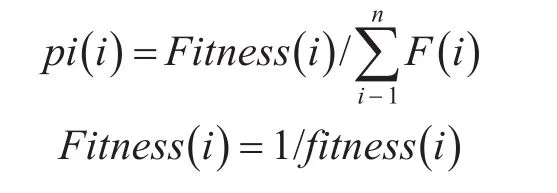
其中pi（i）表示染色體i在每次選擇中被選中的概率。

4）交叉操作

交叉操作創造出的新染色體是推動種群進化的主要因素。交叉操作首先隨機選擇兩個染色體，在每個染色體的前位隨機選擇交叉位置進行交叉操作［9～11］。

5）變異操作

變異操作獲得的新的個體是推動種群進化另一個因素。首先利用變異算子從種群中隨機選取變異個體，然后選擇變異位置S1和S2，最后把個體中S1和S2位的工序和對應的船塢序號交換位置［12］。

6 算例仿真實現

算例可描述為6艘待改造艦艇，在10個船塢內進行改造，除必須首先完成的“拆除軍用武器設備”這一道工序以外，每艘艦艇還需要經歷5道工序，即總共6道工序。試尋找在最短時間內完成所有艦艇改造的優化方案。

首先確定工序的優先級。“拆除軍用武器設備”作為固定的第一道工序，其優先級最大，故只需要比較剩余五道工序。比較是兩兩工序之間進行的比較，根據比較尺度表（見表1）請專家對兩兩工序的重要程度打分。用aij表示第i道工序相對于第j道工序的比較結果，得到比較矩陣A=（aij）。

該比較矩陣A的最大特征值λ=5.073，歸一化特征向量為Ω=［0.263，0.475，0.055，0.099，0.110］。為了判斷五個工序優先級比較結果是否具有一致性，計算總排序一致性比率進行檢驗。

故A通過一致性檢驗。按優先級由大至小的順序分別命名工序為工序2至工序6。

然后，利用多層編碼遺傳算法尋找最優任務分配。利用Matlab 2014a環境中謝菲爾德大學遺傳算法工具箱，按照上文建立的數學模型及多層編碼遺傳算法編程并進行模擬仿真實驗，形成優化方案。每個工序可選擇的船塢編號如表2所示，每道工序在對應船塢內的改造時間如表3所示。

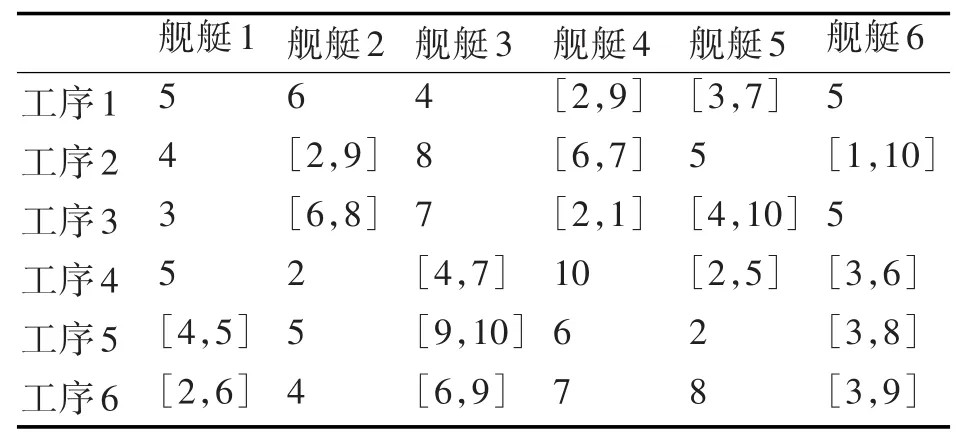
表2 工序可選船塢表

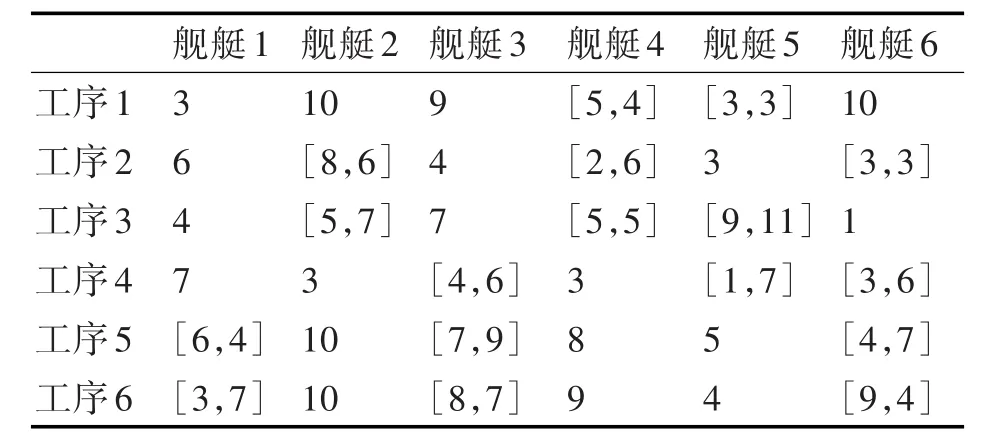
表3 工序改造時間

各參數分別設為種群數量為40，最大遺傳代數為50，交叉率0.8，代溝0.9，變異率0.6。算法搜索得到最優方案的完成時間為49，算法過程和反映最優優化方案的甘特圖分別如圖1和圖2所示。

7 結語

本文主要討論了退役艦艇改造任務分配問題。針對工序多、船塢多、艦艇多的任務特點選擇多層編碼遺傳算法篩選出最優方案，算法經驗證能得到穩定解，效果良好，可以較好應用于多維復雜問題的尋優。本文為退役艦艇改造問題提供了解決方案，對實施項目的進度管理、迅速生成海上執法力量具有一定參考價值。

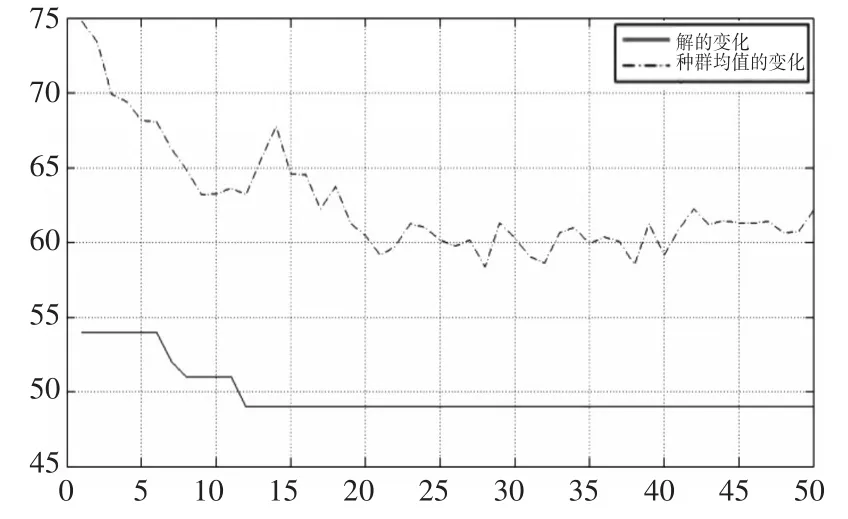
圖1 算法過程

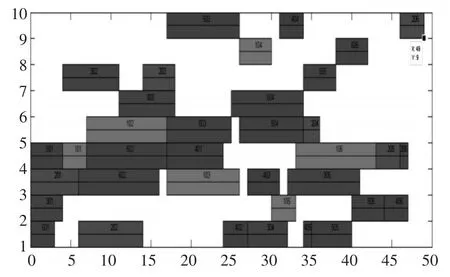
圖2 最優甘特圖