基于改進遺傳算法的柔性車間調度問題的研究?

曹 睿 侯向盼 金巳婷

（1.大連交通大學 大連 116028）（2.中車青島四方機車車輛股份有限公司 青島 266031）（3.沈陽鐵路局通信段 沈陽 110001）

1 引言

在柔性車間調度問題中，每一個部件中的每一道工序不止固定在一臺機器上，可根據具體情況選擇不同的機器加工，并且不同機器加工的時間有所不同，與傳統的車間調度相比更具有靈活性［1］。本次設計利用改進的遺傳算法對柔性車間部件生產完工最大時間最短作為性能指標，確立為目標函數，對種群初始化和交叉變異部分進行改進，提高全局的搜索效率，通過實例說明改進的遺傳算法對柔性車間的調度優化問題有所改善［2］。

2 柔性作業車間調度問題及參數描述

多目標柔性作業車間調度是指生產車間中在m臺設備｛M1，…Mn｝上加工n個工件｛1,…N｝，每個工件包含ni個事先確定加工順序的工序，每道工序可以在多臺設備上加工，每道工序不同的機器加工加工時間有所不同。本文主要考慮最大完工時間最短的性能指標［3］，其目標函數的建立如下：

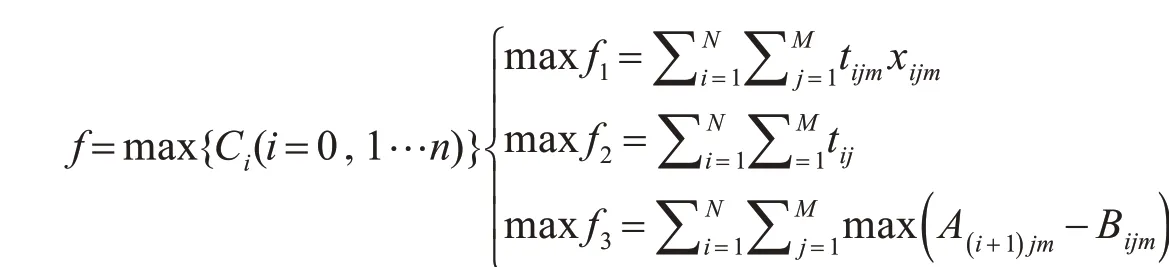
調度目標是為每道工序選擇合適的機器、確定每臺機器上各個工件工序的最佳加工順序以及開工時間，使得工件的最大生產周期最短。除此之外，在工件加工過程中還需要滿足下面的幾個約束條件：1）工件i在機器j上的加工時間需要大于0；2）工件i的加工時間必須在規定時間范圍內；3）對于特定的工件i，機器j必須先于機器m對其進行加工；4）任意工件的加工過程必須是連續封閉的［15］。

一個包含3個工件、5臺機器的FJSP的問題描述如表1所示。

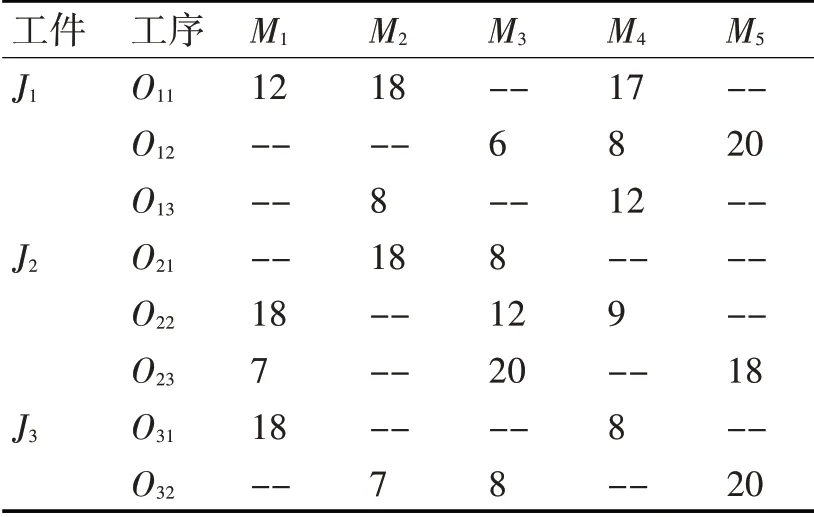
表1 3個工件、5臺機器的柔性車間調度問題

3 算法設計

3.1 染色體編碼

柔性作業車間調度編碼由兩部分組成：一部分是基于機器分配的編碼，對應機器選擇子問題，確定所選擇的加工機器；另一部分是基于工序的編碼，對應工序先后加工的排序子問題，確定工序的先后加工順序［4］。

以3×5柔性車間調度問題為例說明，第一層對工序順序進行編碼得到的加工序列：O11→O31→O21→O12→O22→O32→O23→O13，第二層編碼是基于機器的編碼可以獲得工序對應的加工機器序列：M1→M3→M2→M3→M4→M5→M1→M2。

第一部分是所有工件加工時間

第二部分是機器在加工工件時的準備時間

表示上一工件結束加工時的拖延時間

3.2 種群初始化

根據車間的具體情況，在M個可用機器中選擇k臺性能優良、加工時間相對較短的機器作為一個小規模的初始群體，求出這k臺機器的平均加工時間tA，將剩下的( M-K)臺機器的加工時間tP與tA相比較，為保證初始種群的數量，根據實際情況設置一個tP與tA的差異范圍Q，即若 |tA-tP|∈Q，則保留，否則，該機器淘汰，這樣可以保證初始種群的適應度，提高搜索效率。流程圖如圖1。

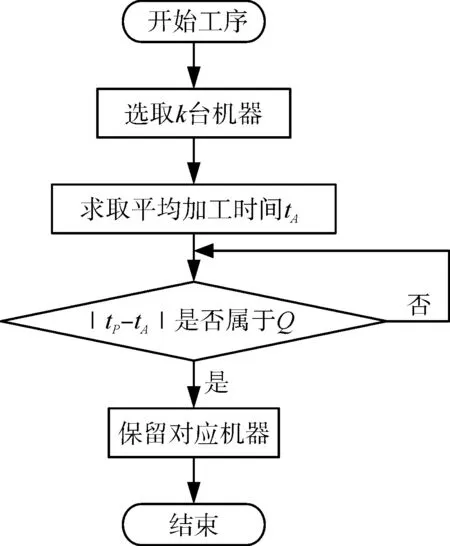
圖1 初始化流程圖

3.3 適應值函數

在遺傳算法中，適應度越高，被選擇的幾率就越大［8］。在本次設計中，將適應度函數表示成目標函數倒數的形式，即

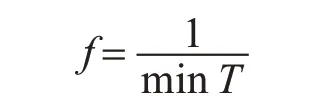
其中min T表示目標函數，即最小生產周期，這樣，當生產周期T最小時，適應度函數值最大，就表示這條加工路線的時間最短［6］。

3.4 選擇操作

首先將種群內個體按適應度大小從高至低排序，利用最優個體保存法將父代中的最優個體即適應度最高的個體直接保留進入到下一代［7］。

3.5 交叉操作

針對FJSP本文提出了兩種交叉操作，第一種是POX交叉操作［11］，用于染色體中工序的加工順序的交叉；第二種是節點交叉操作用于染色體工序分配的機器的交叉。

工序染色體的交叉過程：

P1和P2為父代，交叉后產生子代C1和C2。首先將所有的工件分成兩個集合J1和J2，子一代的染色體C1/C2繼承父代中J1/J2內的工件對應的基因，子一代剩余的部分基因由父代剔除了C1/C2中剩余的基因來補充［9］。

機器染色體的交叉過程：

采用節點交叉法，即將整個染色體的基因串均勻分成三部分，這樣在染色體上就會產生兩個基因位點，選取每個基因位點兩側相鄰的字符組成一個基因段進行交叉，這樣既避免了基因交叉分布的不均勻性，又能提高全局搜索效率［14］。

3.6 變異操作

第一部分變異時，在機器染色體基因串中隨機選擇一個位置，在此工序的機器集中隨機選擇一個與它不相等的整數，替換當前的基因［10］，這樣確保得到的解是可行解。

第二部分采用相鄰交換變異法，以一定的概率隨機選取兩個位置的相鄰基因串進行交換，與交叉操作類似［13］。

3.7 終止條件

本次設計中，根據實際情況，采用設置最大迭代次數的方式來終止算法的執行［12］。

4 仿真結果分析

表2是以6×6的柔性作業車間各工件不同工序加工時間表為例。

表2 6×6柔性作業車間各工件不同工序加工時間

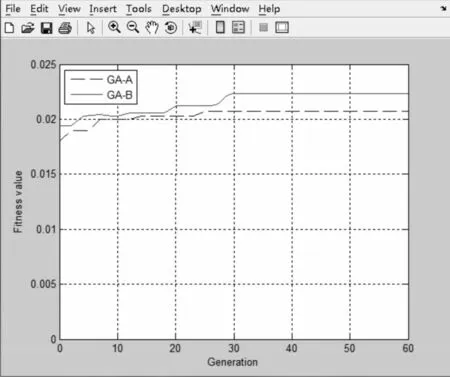
圖2 問題收斂曲線圖

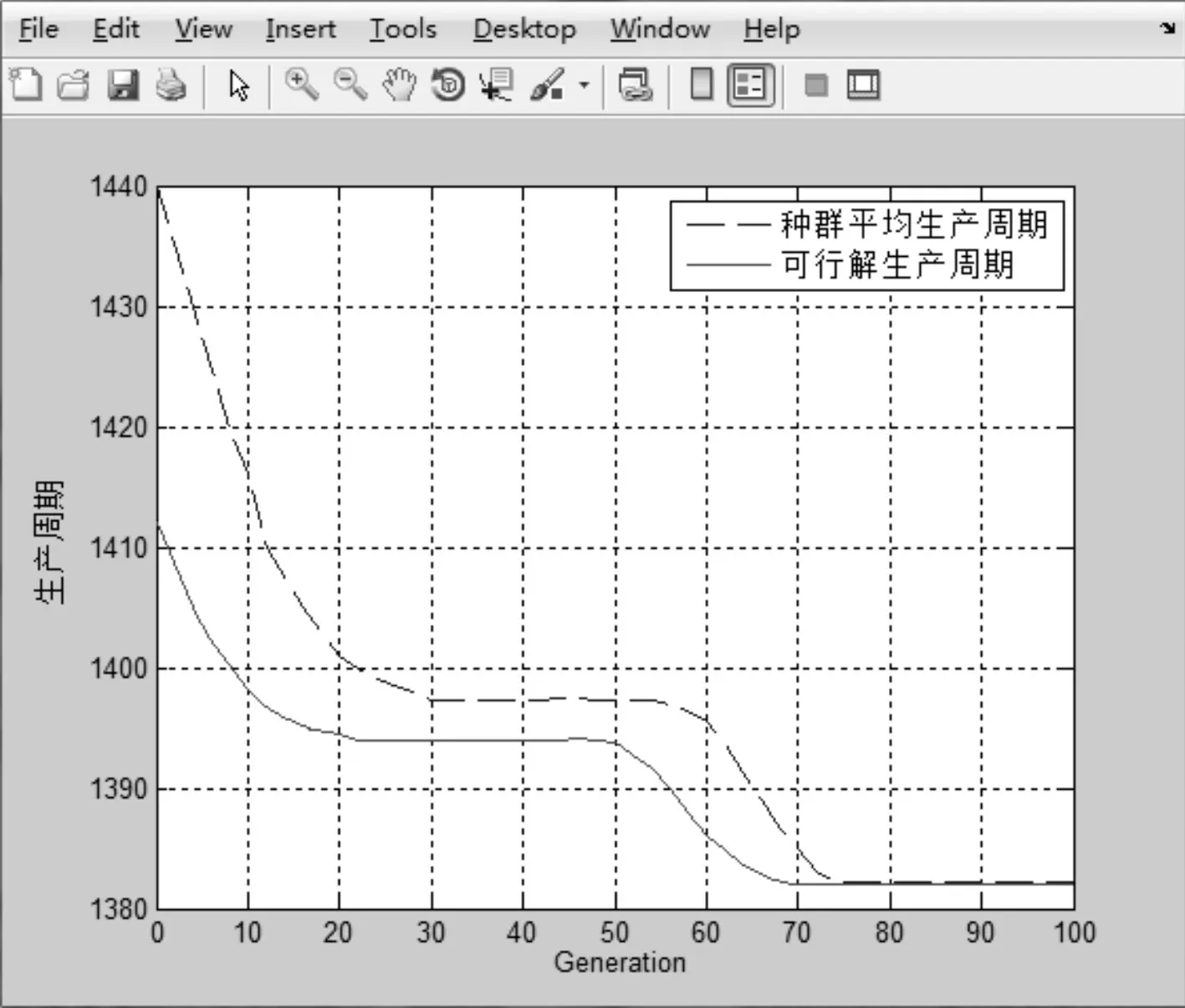
圖3 GA-A迭代曲線圖

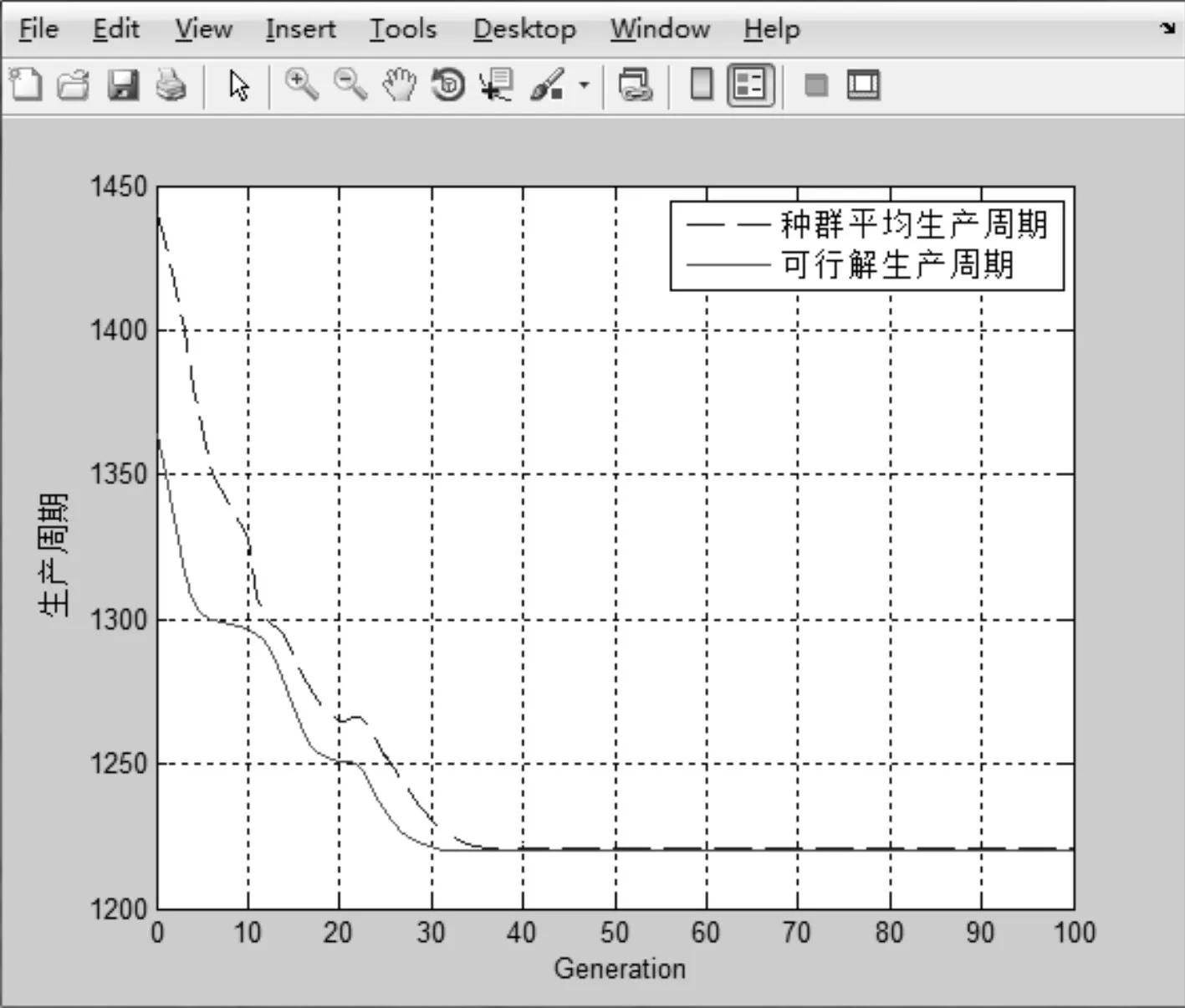
圖4 GA-B迭代曲線圖

5 結語

通過圖2兩種遺傳算法GA-A與GA-B適應度函數的收斂曲線圖可知，本次所設計的遺傳算法相對于傳統算法而言，能夠快速收斂，迅速搜索到最優解，且能夠克服早熟現象，搜索有效穩定；通過對

遺傳算法運行的參數設置如下：種群初始規模S=60，交叉概率Pc=0.8，變異概率Pm=0.01，最大進化代數X=50。將最小生產周期作為適應度函數，并按上述所設置的控制參數，分別基于傳統遺傳算法（GA-A）與本次所設計的遺傳算法（GA-B）對上述實例進行仿真，經過Matlab多次運行仿真后，仿真結果如圖2～4所示。比分析圖3GA-A與圖4GA-B兩種算法的迭代仿真圖像可知，本次所設計的遺傳算法GA-B在30代以內便可收斂至最優解，而傳統遺傳算法GA-A迭代至70代時才收斂至最優解，說明算法GA-B在解決車間實際生產調度問題時更加有效。