畫家和數學的不期而遇

林革

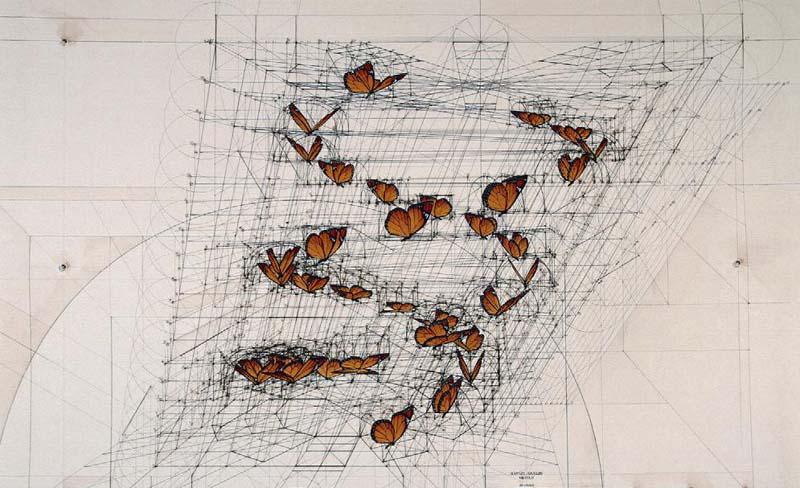
在一般人的印象中，畫家是從事繪畫藝術的人群，以感性思維見長，與培養理性思維的數學似乎并不相干。但你若觀賞過委內瑞拉畫家Rafael Araujor的高能幾何繪畫（圖①和圖②），或許就會改變這樣的想法。他以圓規和尺子做出數學軌跡，就能創作出如此栩栩如生的作品，令人稱奇。由此可見，畫家與數學絕非風馬牛不相及，在心有靈犀和天賦興趣的前提下，藝術時常與數學不期而遇產生奇妙的火花。

畫作中的幻方

中世紀德國著名畫家阿爾布雷特·丟勒在其功成名就之時，突然宣布轉向數學研究，這種跨度似乎很難用心血來潮或別出心裁解釋。即便如此，這位酷愛幻方的畫家為其1514 年的名作《憂郁》（圖③）添加了一個特別背景―四階幻方（圖③右上角），足以顯示自己業余愛好的非凡水準。

用數學眼光來判斷，畫家苦心經營的這個四階幻方看似非常普通。唯一比較特別的是，幻方最后一行中間兩個數是15和14，恰好隱含了作品的創作年代，似乎也僅此而已。由于當時的四階幻方已達880種之多，各有千秋、精彩紛呈，所以人們當初并沒有對畫中的幻方高看一眼。

然而到了本世紀，當專家重新審視這則幻方時，竟然發現數百年來大家都是“有眼不識泰山”，這則幻方中蘊含的種種被忽略的特性足以讓人刮目相看。

第一，幻方角上4數之和16+13+4+1=34，等于四階幻方的和常數，這可不是幻方的常規要求，看似無心卻是有意；第二，在這個幻方中，角上的4個2×2小正方形和中央1個2×2小正方形的4數之和仍等于幻方常數，即16+3+5+10=9+6+4+15=2+13+11+ 8=7+12+14+1=10+11+6+7=34，其中的機巧讓人眼前一亮；第三，在這個幻方中，對角線上8個數字之和等于不在對角線上的8個數字之和，即16+10+7+1+13+11+6+4=2+3+5+ 9+14+15+12+8=68，這顯然出乎人們的意料和想象。

推演后，人們還發現：對角線上8個數字的立方和等于不在對角線上的8個數字的立方和，都為9248。如此“不變其宗”的機變實在讓人拍案叫絕。

一個畫家的數學造詣和精巧構思竟然如此高深，這恐怕是許多人完全沒有想到的。

達·芬奇的巧證

列奧納多·達·芬奇是意大利最著名、最杰出的藝術大師。這位“歐洲文藝復興時期最完美的代表”，學識淵博、多才多藝，不僅在繪畫領域有著高超精湛的藝術造詣，而且在科學領域也展露出非凡卓越的才能，其研究成果和發明創造，曾得到偉大的物理學家愛因斯坦的高度贊賞，被贊譽為“人類歷史上絕無僅有的全才”。下面這則巧證“勾股定理”的故事，應該是對他身份中“藝術家里的數學家”的最佳詮釋。

據說有一天，達·芬奇來畫室檢查學生臨摹《蒙娜麗莎》的情況，令他驚訝的是，竟然有半數學生沒有潛心于作畫，而是在探討“畢達哥拉斯定理”的證明。這個定理也就是大家現在非常熟悉的“勾股定理”：直角三角形兩條直角邊a、b的平方和等于斜邊c的平方，即a2+b2=c2。有關這個定理的證明多種多樣，一直吸引著愛好者另辟蹊徑，嘗試探索。

達·芬奇自然知曉“畢達哥拉斯定理”的出處和背景，加上自身對數學也很癡迷，所以他并沒有批評弟子們，反而饒有興致地加入其中，很快便給出一個別出心裁的證明方法：

先將邊長分別為a、b的兩個正方形和邊長都是a、b、c的兩個直角三角形拼合成圖④，且畫出整個圖形的對稱軸（圖中虛線）；接著，將拼合成的圖形整體從畫紙中移出，再將取出的圖形沿對稱軸剪開，然后保留圖形的左邊，而將右邊按照垂直方向翻轉一周后重新拼合成圖⑤；最后，將圖④中一些頂點相連成一個c為邊長的正方形和兩個邊長為a、b的直角三角形（圖⑥），就完成了定理的證明。

油畫中的難題

俄國著名畫家格丹諾夫·別爾斯基在1895年創作過一幅名為《難題》的油畫（圖⑦）。油畫描繪了一位小學教師正在和他的學生們演算黑板上的數學題。這位戴眼鏡的教師非同尋常，他是俄國著名數學家、教育家拉金斯基。

值得一提的是，這幅與數學有關的油畫的背景。畫中的主人公是莫斯科大學數學教授、著名的教育家拉金斯基，畫中的情景是描繪拉金斯基放棄大都市生活，到農村當一名默默無聞的小學教師。或許人們都會驚訝于拉金斯基的選擇，其實只要了解了拉金斯基的生活經歷就不難理解。生于農村的拉金斯基自小便對數學產生了濃厚的興趣，常常為了一些“難題”，算上幾天幾夜也不疲倦。11歲那年，他碰到一道難題，徒步50多千米到城里求教中學老師，老師只花了一分鐘，便解出了答案。所以他很有感觸：一些令農村孩子們頭疼的“難題”，只要有好的老師指導，其實是很簡單的。

為改變這種情況，拉金斯基盡管依靠自己的努力成為俄國著名數學家，他還是毅然辭去大學教授的職位，選擇回到農村，來到那些更需要他的孩子們身邊。這幅油畫也由于數學家拉金斯基的感人事跡而得到了人們的關注。

這幅油畫被世界各地的數學愛好者得知后，大家紛紛前去品鑒，其中就有美國著名數學科普大師加德納。由于職業關系，加德納對畫中的這道數學題產生了濃厚興趣，他循著這一問題進行了有針對性的研究，一番艱辛之后，終于有所發現。

之后，又經過進一步深入演算，加德納終于歸納出了這樣一個規律：這些等式可以無窮無盡地寫下去，樣子就像一座美麗的“寶塔”。如果等式右邊有x項，那么等式左邊就有x+1項。當然，所有的數都得平方。加德納說，最關鍵的是，這一串連續自然數中心的一個，一定為2x（x+1）。這可是從這幅特殊的油畫中得到的特殊發現喲。

杰作中的數學公式

文森特·威廉·梵高是19世紀偉大的藝術巨匠，也是舉世聞名的印象派大師。他的一生歷經艱難困苦。梵高在世時，其藝術造詣并未得到充分肯定，他飽受癲癇病和精神錯亂的折磨，甚至割掉了自己的一只耳朵，最終在37歲時于絕望中開槍自殺。與此同時，梵高的一生又取得了輝煌的成就，如今，他已成為人們心目中偉大的藝術家，其畫作不斷被拍出高價，在藝術史上達到了令人難以超越的高度。

更耐人尋味的是：在被視為經典的梵高后期作品之《麥田上的烏鴉》（圖⑧）以及《星空》（圖⑨）里，科學家用獨特的眼光發現了非比尋常的元素，畫作中一些旋渦式圖案背后竟然暗藏著復雜的數學和物理學公式。

在這幅《麥田上的烏鴉》中，烏云翻卷的天空和狂風撼動下的麥田，急促而蒼勁的黑色線條，畫出在波浪起伏的麥田上低掠而過的烏鴉。畫中的每筆線條都帶有強烈的動感，動蕩不安的構圖、明暗對比強烈的色調、粗野狂放的繚亂筆觸，充分顯露出梵高內心的孤獨、壓抑和苦悶。

在《星空》中，畫著一些小屋， 絲柏從地面伸向夜空；黃色的星星與閃光的橘黃色月亮形成旋渦， 天空因此變得活躍起來。

在這兩幅作品中，幾乎所有人都能感受到旋渦的存在和作用，一直以來，人們把這些旋渦看成是梵高的一種獨特的藝術表現形式，但現在，來自墨西哥國立自治大學的物理學家喬斯·阿拉貢經過研究發現，梵高畫作里出現的那些深淺不一的旋渦，竟然和半個世紀后科學家用來描述湍流現象的數學公式不謀而合。

湍流問題曾被稱為“經典物理學最后的疑團”，科學家一直試圖用精確的數學模型來描述湍流現象，但至今仍未徹底解決。20世紀40年代，蘇聯數學家柯爾莫哥洛夫提出了“柯爾莫哥洛夫微尺度”公式，借助該公式，物理學家可以預測流體任意兩點之間在速率和方向上的關系。在梵高的這兩幅畫作里，那些深淺不一的旋渦正好精確地反映了這個公式。

需要指出的是，梵高這些畫作均為其后期作品，當時的他已經陷入癲癇病帶來的內心狂亂狀態，時而清醒，時而混亂。阿拉貢相信，正是梵高的幻覺讓他得以洞察旋渦的原理。持類似觀點的還有哈佛大學神經病學教授史蒂文·沙克特，他認為：“有人會在發病時產生新的、異常的意識，他的感覺和認知都會變得不正常。”換句話說，梵高畫作里表現出的物理現象，極有可能與其受癲癇病影響有關。科學家們相信癲癇令梵高產生的幻覺，可能賦予他洞察湍流奧秘的特殊能力，并不自覺地在作品中留下湍流的經典數學模型的影像。

盡管這樣的解釋并不能完全令人信服，但這種藝術與科學的碰撞，或許與梵高天才的想象和苦行僧般的經歷有關，冥冥之中的注定恐怕只可意會，難以言傳，因此我們在對科學家的發現表示驚訝的同時，也只能對這位藝術大師的傳奇表達敬意。

埃舍爾的錯覺圖形

莫里茨·科內利斯·埃舍爾是荷蘭科學思維版畫大師，20世紀畫壇中別具一格的藝術家。其作品多以平面鑲嵌、不可能的結構、悖論以及循環等為特點，從中可以看到對分形、對稱、雙曲幾何、多面體、拓撲學等數學概念的形象表達，為繪畫藝術增添了難以言說的數學之美，他也被公認為將繪畫藝術性與數學科學性融會貫通并發揮到極致的藝術大師。

1956年，埃舍爾舉辦了生平第一次重要的畫展，這個畫展得到了《時代》雜志的好評，使他在世界范圍獲得了極高的名望。許多數學家給予埃舍爾藝術作品充分的肯定，認為埃舍爾藝術作品中的數學原則和思想得到了非同尋常的形象化。后來，隨著埃舍爾創作的發展，創造出許多反映悖論和“不可能”的圖形結構的藝術作品，見者莫不驚嘆于數學思維融入藝術創造中的奇特魅力。

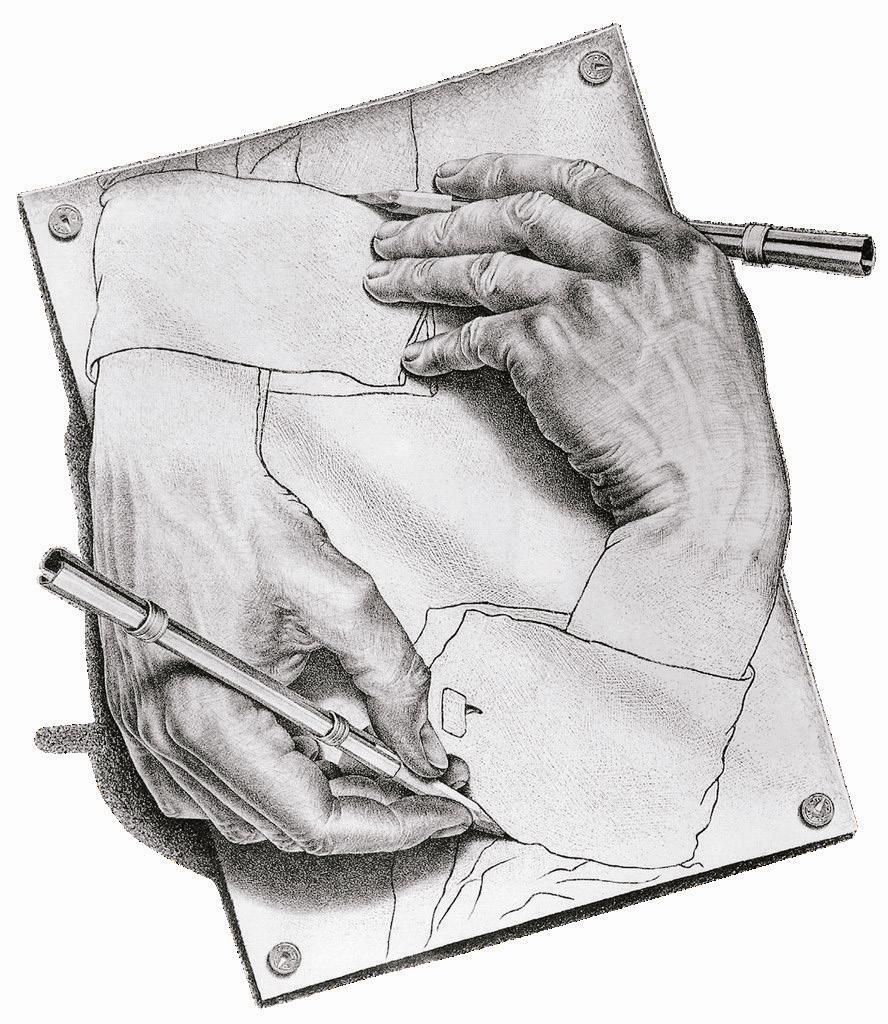
比如上面這幅引人注目的作品《互繪的雙手》（圖⑩），你看到后會情不自禁地研判究竟是哪一只手繪出了另一只手。畫面中既像左手畫著右手，又像右手畫著左手，當然也可以看作左右手互繪，在確定無解后只能感慨“你中有我，我中有你”的神奇。而這恰好反應了埃舍爾作品中極為重要的特征—自我復制和完全循環。事實上，在埃舍爾其他代表作品中，這種特征隨處可見，已成特色，并由此營造出匪夷所思的視覺效果。

不僅如此，埃舍爾的許多作品還體現了平面鑲嵌的特點。所謂“平面鑲嵌”，是指完全沒有重疊并且沒有空隙的封閉圖形的排列。一般情況下，構成鑲嵌的封閉圖形的基本單元是多邊形或類似的常規形狀，埃舍爾更癡迷于那些不規則的、形狀特別的平面鑲嵌。因此，在他的很多藝術作品中，都運用了幾何學中的反射、旋轉來得到更加多變的圖案，并獨具匠心地使這些圖案通過扭曲、變形成為人、鳥、魚等，這樣美不勝收的效果既自然又令人拍案叫絕。比如《騎士平面鑲嵌》（圖〇11）和《黑白鳥的鑲嵌》（圖〇12）就充分反映出重疊、翻轉的數學美。

此外，交叉幾何體也常常出現在埃舍爾的藝術作品中，比如木版畫《星空》（圖13〇）：這是一個由八面體、四面體和立方體交叉構成的幾何體，這些正面體都是外凸的，同時還存在內凸的正多面體，數學家已證明出存在26種可能的規則立體，它們之間互相交叉后還可以形成無數規則的立體系列。埃舍爾設計出飄浮著無數規則立體的星空背景，并在奇妙的正多面體中加入了兩條變色龍，帶給觀眾奇妙的視覺沖擊，巧妙展現出了立體幾何的數學美。

特別值得一提的是，在埃舍爾用數學觀點完成的所有重要藝術作品中，最重要的是處理空間性質的作品。比如《瀑布》（圖〇14），從中可以發現這個瀑布本質上就是兩個彭羅斯三角的疊加，形成了矛盾的空間，顯示了埃舍爾對空間維度的關注以及用二維的方式表現三維空間的矛盾和詭術。

所謂彭羅斯三角 （圖〇15），看起來像是一個固體，由三個截面為正方形的長方體所構成，三個長方體組合成為一個三角形，但兩長方體之間的夾角似乎又是直角。但上述性質無法在任何一個正常三維空間的物體上實現，是所有不可能圖形中最基礎的一個。

在埃舍爾手中，剛性的維度可以任意扭曲反轉，從而展示出在其豐富想象空間中的魔法變換。

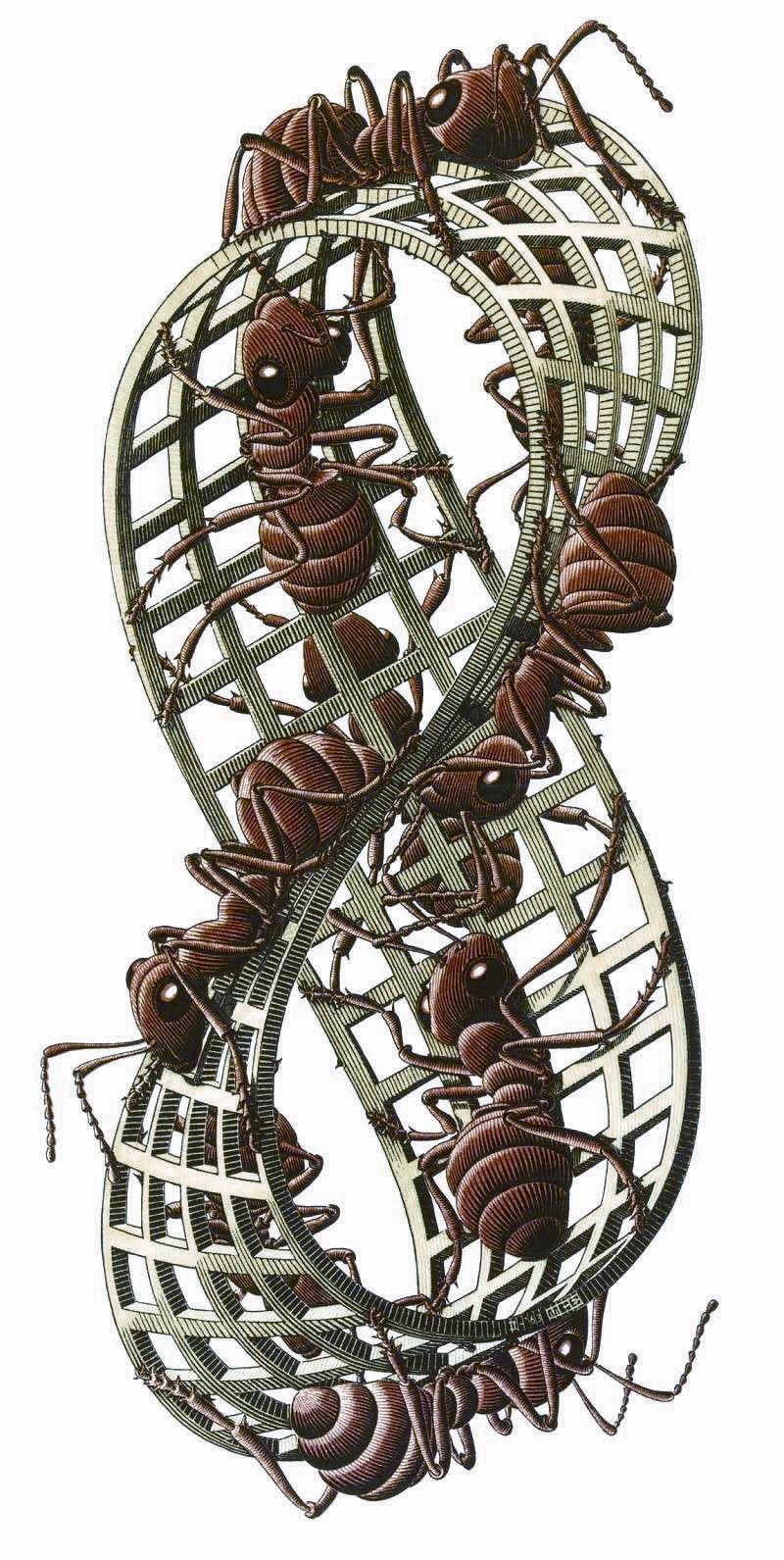
在《莫比烏斯帶上的螞蟻》（圖〇16）中，如果我們跟蹤螞蟻的路徑，就會發現螞蟻并不是在相反的面上爬行，而是爬行在同一個面上。這就是埃舍爾藝術作品中展現出的拓撲學價值和數學美。

早在公元前6世紀，古希臘著名數學家畢達哥拉斯就認為：數與美緊密關聯，甚至可以說，數是美的本源，一切藝術都產生于數。這足以說明藝術與數學有著悠遠的淵源。由此不難理解，從事藝術創作的畫家為何流連于鮮花盛開的數學園林，探尋和呈現數學之美才是主線和主題。