例析數學素養在中學數學中的具體體現

莫靜波 陳國林

(1.山東省鄒平市教研室 256200；2.東華理工大學 330013)

數學學科核心素養的培養，要通過學科教學和綜合實踐活動課程來具體實施。下面我們具體從實例中去賞析數學試題中所體現的核心素養。

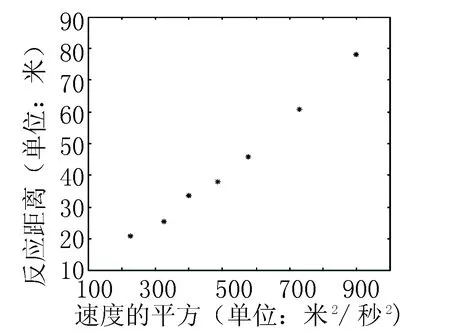
案例(2018廣西南寧第二次適應性考試)隨著人們對交通安全的重視，安全駕駛已成為了社會廣泛關注的問題.交通管理部門調取了大量數據，得到以下散點分布圖其中y表示“反應距離”，指的是駕駛員從作出反應(剎車)到車輛停止滑行的距離(單位: 米)，x表示駕駛員作出反應的瞬間車輛速度的平方(單位: 米2/秒2).

x-y-w-519.714343.172722.2857∑7i=1(x--xi)2∑7i=1(w--wi)2∑7i=1(x--xi)(y--yi)∑7i=1(w--wi)(y--yi)332350161.428628486618.5575

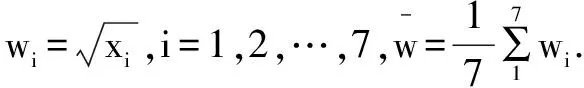
(2) 根據(1)的判斷結果和表中的數據，建立y關于x的回歸方程;

(3) 當駕駛者看到前方30米處出現行人并剎車，根據(2)中你得到的方程，請說明此時駕駛者的速度滿足什么條件才能避免這次車禍?

附：對于一組數據(x1,x1)，(x2,x2)，…，(xn,xn)，其中回歸方程y=α+βx的斜率和截距的最小二乘估計分別為：

素養解讀數學核心素養在此題中能夠充分得到體現，本題以生活中的實際出發，通過對數據收集并整理，繪制出的散點圖，并依據散點圖對具體問題進行分析，潛移默化地注入了數據處理數學核心素養，考生需要將實際問題與數學問題進行轉化，因此需具備數學抽象的能力，求解線性回歸方程，強調了統計學的模型思想.第1問設置依據散點圖判斷散點圖所適合的模型問題，需要學生具備一定的邏輯推理能力，方能進行判斷，所以第1問的設計能夠有效地滲透邏輯推理思想。直觀想象能力是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解解決數學問題。此題需要借助幾何直觀能力，依據散點圖進行答題。整個試題中都需要進行數學的運算，能夠有效地對學生的數學運算能力進行考查。

解題思路此題所給的散點圖至關重要，需要依據散點圖結合所給函數的圖象選擇適定的擬合函數。選定函數后利用題中所給公式求出β，α的值便可求得y關于x的線性回歸方程。最后令y<30，即可求得x的范圍，從而確定w滿足的條件。

得分展示(1)y=ax+b更適合于模型

(2)根據最小二乘法公式

(3)要求不發生車禍，需要滿足y=0.0857x-1.3668<30

故x<366.007，即w<19.1313.此時車速滿足小于19.1313米/秒才能避免這次車禍

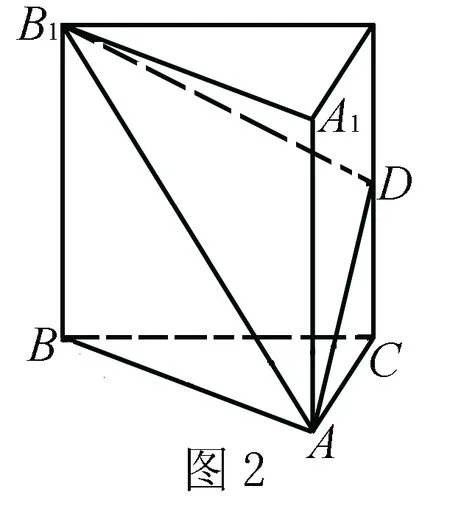
跟蹤訓練(2018黑龍江齊齊哈爾一模)如圖所示，正三棱柱ABC-A1B1C1的底面邊長為2，D是側棱CC1的中點.

(1)證明:平面AB1D⊥平面ABB1A1；

試題解析(1)如圖①，取AB1的中點E，AB的中點F，連接DE,EF,CF，易知EFBB1，又∴四邊形CDEF為平行四邊形，∴DE∥CF.又三棱柱ABC-A1B1C1是正三棱柱，∴ΔABC為正三角形，∴CF⊥AB.又CF?平面ABC，CF⊥BB1,而AB∩BB1=B，∴CF⊥平面ABB1A1.又DE∥CF，∴DE⊥平面ABB1A1.

又DE?平面AB1D，所以平面AB1D⊥平面ABB1A1

(2)(方法一)建立如圖①所示的空間直角坐標系，

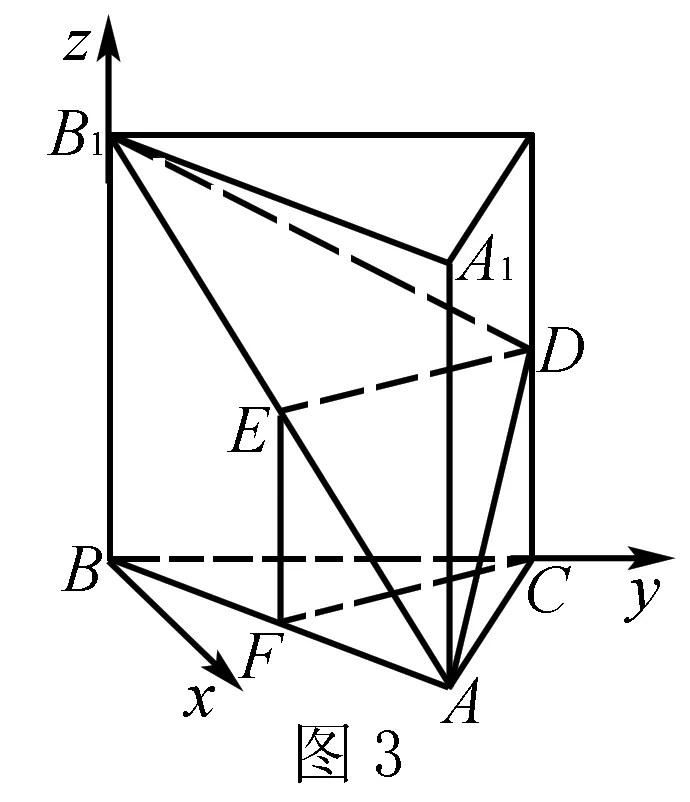
顯然平面ABC的一個法向量為m=(0,0,1)，

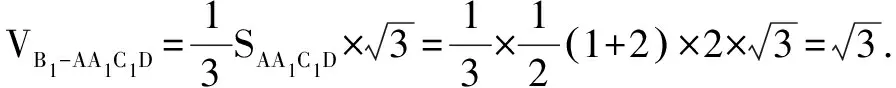
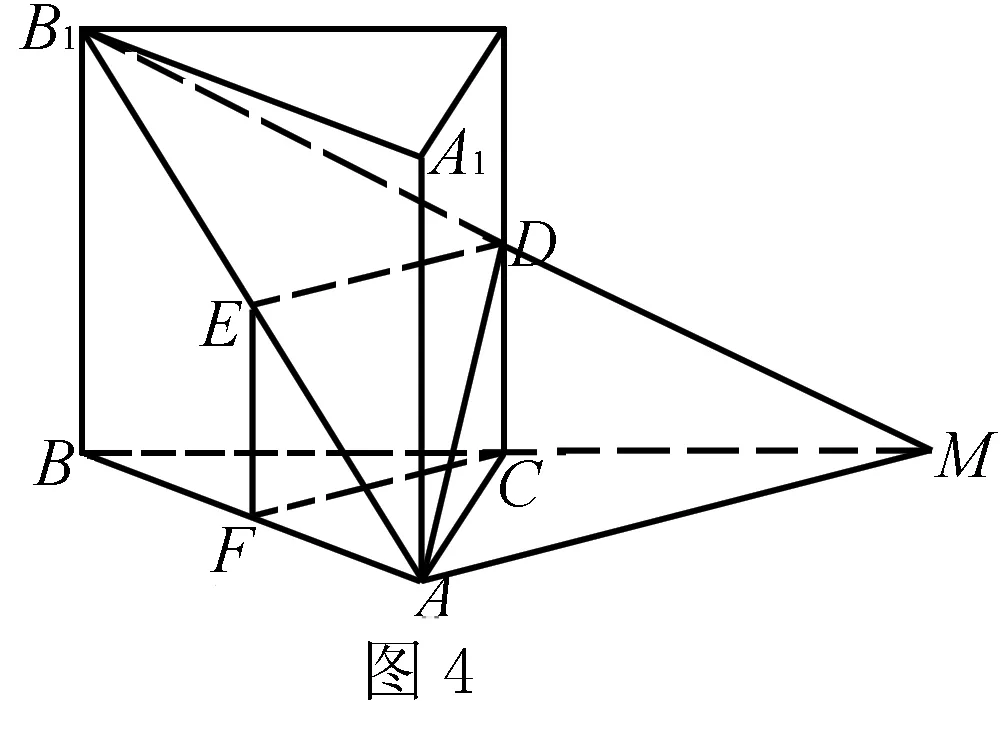
方法二如圖2，延長B1D與BC交于點M,連接AM.

∵B1C1∥BC,D為CC1的中點，∴D也是B1M的中點,又∵E是AB1的中點,∴AM∥DE.

∵DE⊥平面ABB1A1,∴AM⊥平面ABB1A1.

∴∠B1AB為平面AB1D與平面ABC所成二面角的平面角.

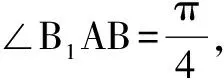
愛因斯坦說過：“提出一個問題往往比解決一個問題更重要。”提問能夠促進課堂氛圍，提高學生的注意力，更能有助于了解學生的具體情況。課堂教學過程中要注意數學核心素養的重要性，但又不能花出很大的時間去講述數學核心素養，因此在整個教學中通過問題滲透是一種不錯的教學手段，提問便是一種檢測的手段。其實當你慢慢學會解題的過程中，你的數學核心素養就已經在慢慢的提高了。