以正(長)方體模型為依托 巧解立體幾何選(填)題

張桂華 沈加法

(云南省蒙自市第一高級中學(xué) 661199)

正(長)方體是點、線、面位置關(guān)系和數(shù)量關(guān)系的重要載體，正(長)方體模型是立體幾何中的兩個重要模型，以正(長)方體模型為載體研究和學(xué)習(xí)立體幾何問題是新課標(biāo)的要求.一方面，正(長)方體由于其圖形本身對稱完美，所含的線線、線面、面面的位置關(guān)系內(nèi)容豐富，各種角度及距離均可在其中得以體現(xiàn)，堪稱立體幾何中的“萬花筒”，是研究線線關(guān)系、線面關(guān)系、特殊幾何體的重要載體.另一方面，許多立體幾何的基本概念與定理可以在正(長)方體中得到反映，很多空間幾何體可由正(長)方體切割而成，加之正(長)方體是學(xué)生在日常生活中最常見、最熟悉的一種幾何體，如果教師在教學(xué)中能引導(dǎo)學(xué)生挖掘題設(shè)條件,展開聯(lián)想、類比，引進(jìn)旨在求解的輔助元素——正(長)方體模型,即將所求幾何體補成正(長)方體或?qū)⑵浞湃胝?長)方體中，原幾何體的一些位置關(guān)系和數(shù)量關(guān)系將會變得一目了然，學(xué)生將會增強對空間圖形的變換與綜合，許多立體幾何選(填)題將能得到巧解，可收到事半功倍之功效.下面談?wù)勎以诮虒W(xué)中引導(dǎo)學(xué)生解立體幾何選(填)題的一些做法，僅供大家參考.

一、以正(長)方體模型為依托，將幾何元素安插其中，對號入座，巧解立體幾何選(填)題

例1 設(shè)m，n是兩條不同的直線，α，β是兩個不同的平面，下列命題中正確的是( ).

A．若α⊥β，m?α，n?β，則m⊥n

B．若α∥β，m?α，n?β，則m∥n

C．若m⊥n，m?α，n?β，則α⊥β

D．若m⊥α，m∥n，n∥β，則α⊥β

分析本例中的線、面關(guān)系較為復(fù)雜，學(xué)生一時不易想象空間圖形的位置關(guān)系，作圖也相對較難，但若注意到4個選項中涉及的兩條直線或兩個平面不是垂直就是平行，如能以正(長)方體模型為依托，將題設(shè)中的線面關(guān)系放入正(長)方體中，對號入座，則各種線面關(guān)系將一目了然.

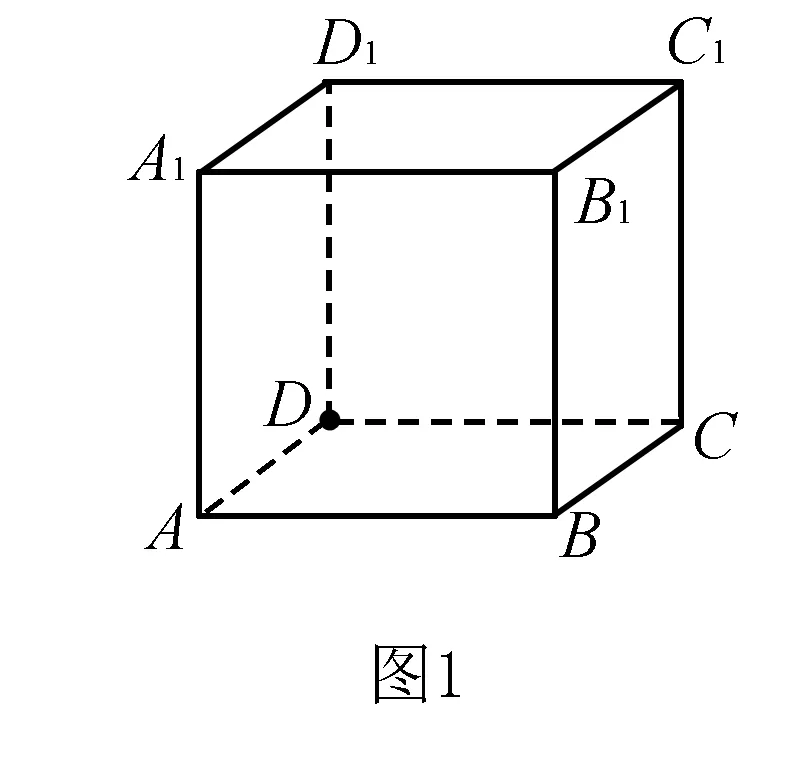
如圖1所示：對于A：設(shè)平面ABCD為α，平面B1BCC1為β，設(shè)AD所在直線為m，B1C1所在直線為n，如圖所示，顯然有α⊥β，且m?α，n?β，但m⊥n不成立，故命題A不正確；對于B：設(shè)平面ABCD為α，設(shè)平面A1B1C1D1為β，設(shè)AD所在直線為m，D1C1所在直線為n，顯然有α∥β，且m?α，n?β，但m∥n不成立，故命題B不正確；對于C：設(shè)平面ABCD為α，設(shè)平面A1B1C1D1為β，設(shè)AD所在直線為m，D1C1所在直線為n，顯然有m⊥n，但α⊥β不成立，故命題C不正確．綜上所述，故選D．

例2 在空間四邊形ABCD中，AB⊥BC,BC⊥CD,CD⊥AB，且AB=BC=CD，則AD與BC所成角的正切值為____.

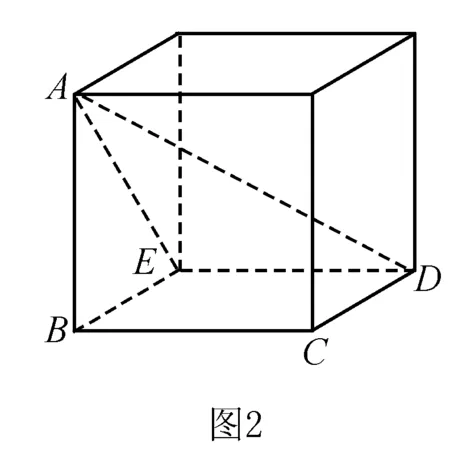
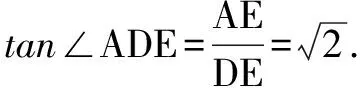
例3 已知直線a和平面α、β，α∩β=m，a?α，a?β，a在α,β內(nèi)的射影分別為直線b和c,則b,c的位置關(guān)系是( ).

A．相交或平行 B．相交或異面

C．平行或異面 D．相交，平行或異面

分析本例中的線、面關(guān)系較為復(fù)雜，學(xué)生不易想象空間圖形的位置關(guān)系，作圖難度較大，但若能以長方體模型為依托，將題設(shè)中的線面關(guān)系安插長方體中，對號入座，則各種線面關(guān)系將一目了然.如圖3，構(gòu)造符合題條件的長方體，將動直線a放入如圖所示的3種位置，不難看出射影b和c有3種位置關(guān)系：相交，平行或異面.故選D．

例4 到兩互相垂直的異面直線的距離相等的點( ).

A．只有1個 B．恰有3個

C．恰有4個 D．有無窮多個

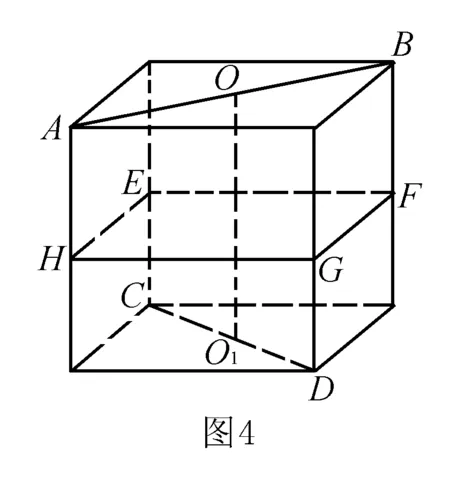
分析本題對學(xué)生來說較為抽象、復(fù)雜，難度較大，但若能以正方體模型為依托，將題設(shè)中的線線關(guān)系安插正方體中，對號入座，問題就會變得直觀.如圖4所示，顯然，線段OO1、EF、FG、GH、HE的中點到兩垂直異面直線AB、CD的距離都相等，所以排除A、B、C，故選D．

小結(jié)：涉及空間想象能力的一些線線、線面和面面位置關(guān)系的立體幾何選(填)題，常可以正(長)方體模型為依托，運用正(長)方體中的線、面來驗證或找出反例.

二、以正(長)方體模型為依托，在正(長)方體中構(gòu)造棱柱、棱錐，可增強幾何直觀，進(jìn)而發(fā)現(xiàn)幾何體間固有的依存關(guān)系，巧解立體幾何選(填)題

荷蘭數(shù)學(xué)教育家弗賴登塔爾說：“數(shù)學(xué)是在內(nèi)容和形式的相互影響之中的一種發(fā)現(xiàn)和組織活動.”從形式上看，棱柱、棱錐等幾何體與正(長)方體模型無關(guān)，但從內(nèi)容上看，垂直、平行，共球等性質(zhì)卻是這些幾何體都共同具有的，因此，我們應(yīng)善于從不同幾何體間的相互影響之中來發(fā)現(xiàn)他們的內(nèi)在聯(lián)系，進(jìn)而有目的性地組織我們的解題思路.

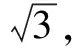
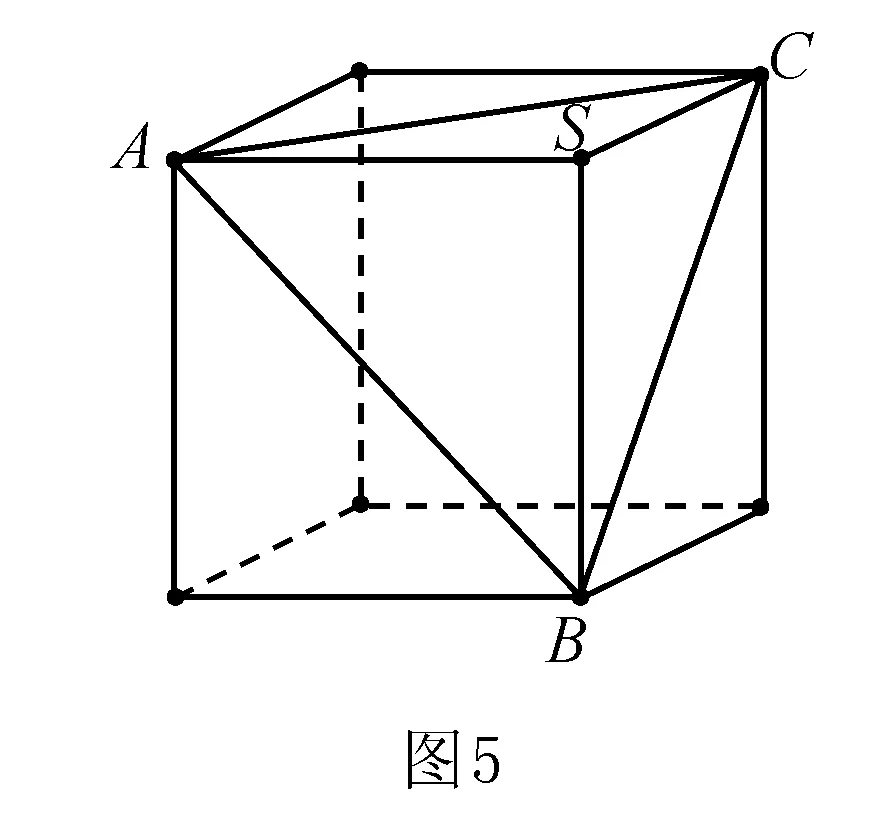
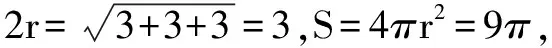
例6 在四棱錐的四個側(cè)面中，直角三角形最多有____個.

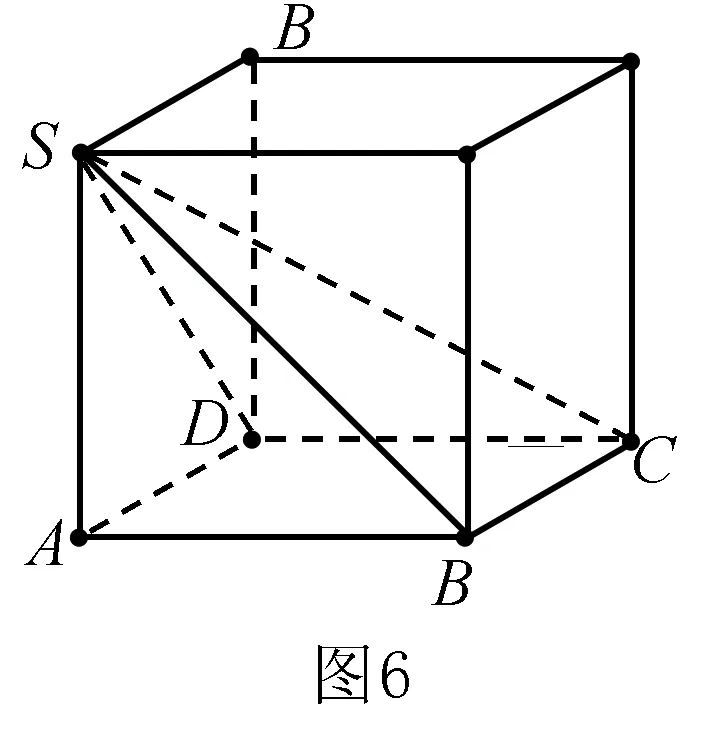
分析有2個直角三角形學(xué)生容易想到，但最多有幾個就很難想了，靠推理論證似乎題設(shè)條件太少，也顯得有些小題大做.但如能以正方體模型為依托，在正方體中構(gòu)造如圖6所示的四棱錐S-ABCD，則不難證明四個側(cè)面均為直角三角形，故有4個.

例7 如圖7，網(wǎng)格紙上小正方形的邊長為1，粗實線畫出的是某多面體的三視圖，則該多面體的各條棱中，最長的棱的長度為( )

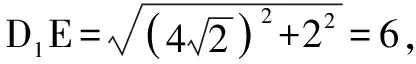
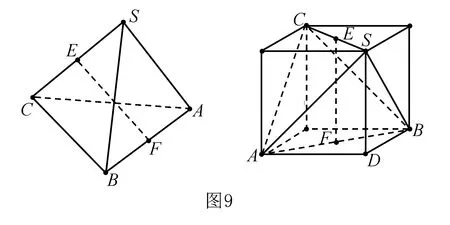
例8 如圖9，已知正三棱錐S-ABC的側(cè)棱與底面邊長相等，E，F(xiàn)分別為SC，AB的中點，那么異面直線EF與SA所成角為____.

分析本例中通過中點作平行線，找到異面直線所成角困難較大，其次要熟悉正三棱錐的對棱互相垂直這一隱含性質(zhì)，否則，解決本題確有一定難度，但若能以正方體模型為依托，在正方體中構(gòu)造如圖10所示的正三棱錐S-ABC，則容易看出SA與SD的所成角即為異面直線EF與SA所成角，顯然∠ASD=45°.另外，我們還可直觀地看到：正三棱錐的對棱互相垂直這一性質(zhì).

小結(jié)：棱柱、棱錐不是孤立的幾何體，它和正(長)方體有著千絲萬縷的聯(lián)系，若能以正(長)方體模型為依托，把棱柱、棱錐放入正(長)方體中，不僅能彰顯事物間的本質(zhì)聯(lián)系，所求問題會變得直觀，解決問題的途徑自然也就多了.

三、以正(長)方體模型為依托，化抽象為直觀，把解決多面體與球的有關(guān)問題與正(長)方體聯(lián)系起來，巧解立體幾何選(填)題

由于正方體的特殊性，它存在一個外接球和一個內(nèi)切球，因而有關(guān)多面體與球的諸多幾何問題可以通過正方體模型來解決.

例9 已知點P，A，B，C均在同一球面上，如果PA，PB，PC兩兩互相垂直，且PA=PB=PC=a，則這個球的表面積為____．

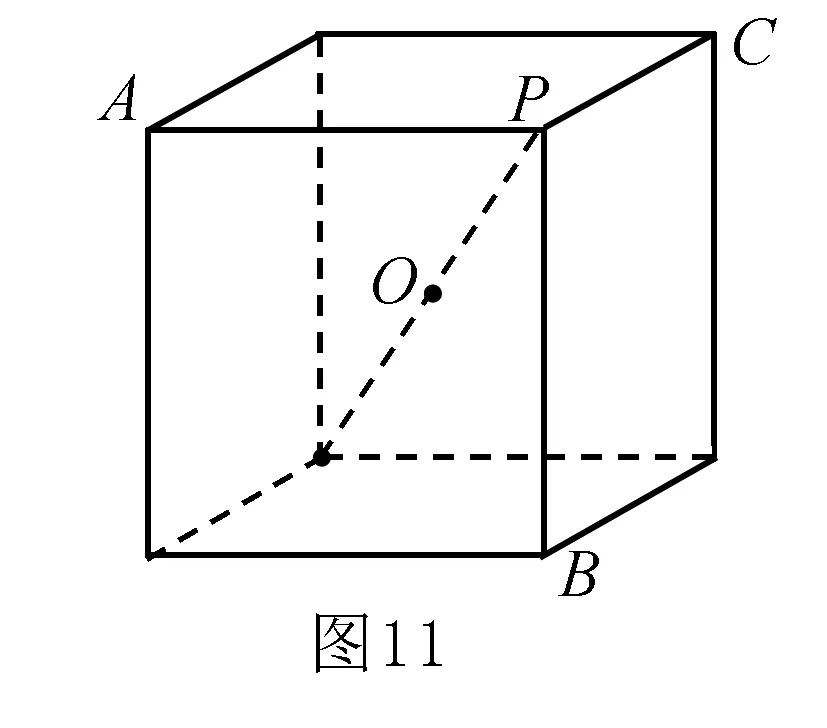
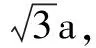
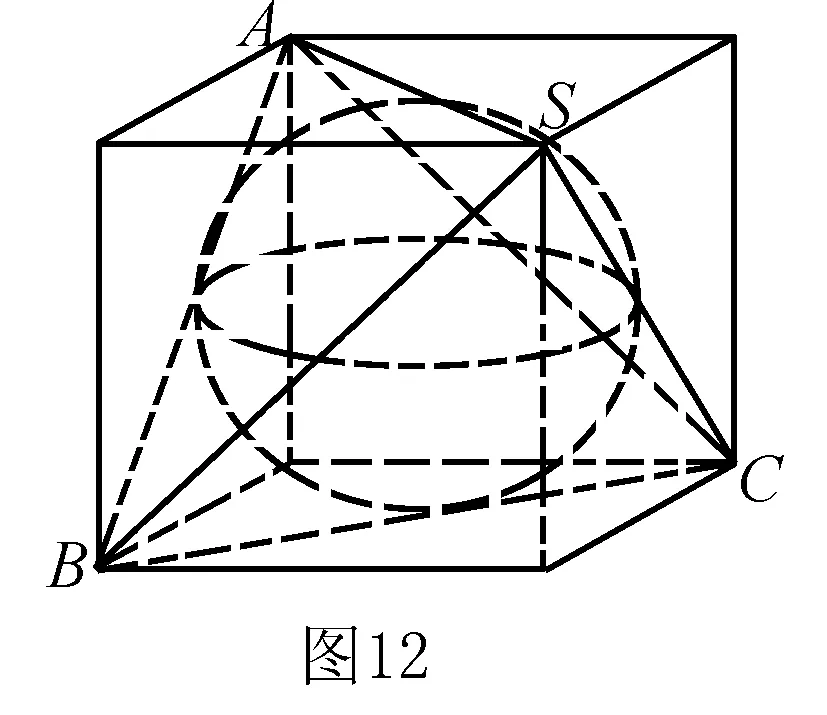
例10 已知一個正四面體的棱長為a,有一個球和它的六條棱都相切，則這個球的體積為____.

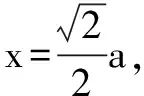
小結(jié)：由于畫與球相關(guān)的幾何直觀圖難度較大、給解題帶來了困難，所以解決多面體與球有關(guān)的幾何問題時應(yīng)以正(長)方體為模型，將其進(jìn)行等價轉(zhuǎn)化，不要在畫圖上浪費時間，我們要做到“不畫球，但心中有球”. 并且還要善于從不同幾何體間的相互影響中來發(fā)現(xiàn)他們的內(nèi)在聯(lián)系，進(jìn)而有目的性地組織我們的解題思路，從而使多面體與球的有關(guān)問題得以巧解.

總之，在立體幾何解題教學(xué)中若能以正(長)方體模型為依托，是對“數(shù)學(xué)是一種發(fā)現(xiàn)和組織活動”，“數(shù)學(xué)是一種創(chuàng)造性過程的歸納科學(xué)”的實踐檢驗.立體幾何試題由于線面關(guān)系復(fù)雜,加之部分學(xué)生空間想象能力弱，因而對立體幾何的學(xué)習(xí)往往感到畏懼.如果教師在教學(xué)中能引導(dǎo)學(xué)生挖掘題設(shè)條件,展開聯(lián)想、類比，引進(jìn)旨在求解的輔助元素——正(長)方體模型，即若能以正(長)方體模型為依托，將所求幾何體補成正(長)方體或?qū)⑵浞湃胝?長)方體中；或在正(長)方體中構(gòu)造棱柱、棱錐，增強幾何直觀，進(jìn)而發(fā)現(xiàn)幾何體間固有的依存關(guān)系，化抽象為直觀；或把解決多面體與球的有關(guān)問題與正(長)方體聯(lián)系起來，這樣原幾何體的一些位置關(guān)系和數(shù)量關(guān)系將會變得一目了然，學(xué)生將會增強對空間圖形的變換與綜合，許多立體幾何選(填)題將能得到巧解，進(jìn)而可收到事半功倍之功效.