滴灌管主流道沿程壓力分布模型及驗證

丁法龍，茅澤育，王文娥，韓 凱

?

滴灌管主流道沿程壓力分布模型及驗證

丁法龍1，茅澤育1，王文娥2，韓 凱1

（1. 清華大學水利水電工程系，北京 100084；2. 西北農林科技大學旱區農業水土工程教育部重點實驗室，楊凌 712100）

為揭示滴灌管的沿程流動特性，簡化滴灌水力計算，分析了能量方程應用于滴灌管水力計算的局限性，并以質量守恒和動量守恒定理為依據，建立了以滴灌管為典型的變質量流動數學模型，并結合測壓試驗數據，獲得了滴灌管主流道沿程壓力分布表達式。變質量流動的動量方程表明：多孔管路主流道壓力變化取決于摩阻項和動量交換項兩部分，沿程壓力分布的具體形式取決于二者作用的相對強弱，滴灌管壓力分布歸結為求解滴灌管軸向流速分布、摩阻系數和動量交換系數，動量方程建立的合理之處在于不必追究其詳細機制，將復雜的流動機理進行了合理概化。測壓-測流試驗表明：滴灌管軸向流速分布指數與滴頭自身特性參數無關，而與滴頭安裝個數呈線性關系。基于理論分析和試驗數據回歸得到了動量交換系數的表達式，并結合Blasius摩阻公式進行方程求解，壓力計算值與實測值吻合良好，最大相對誤差為4.27%。該文可為滴灌管水力計算及多孔管水動力學研究提供一定參考。

灌溉；模型；壓力；主流道；變質量流動；摩阻作用；動量交換

0 引 言

滴灌作為一種精準灌溉技術，節水效果顯著，更加省工、增產，因而在農業生產中得到了快速推廣應用[1]。灌水均勻度是滴灌質量評估和水力設計的核心指標[2]，其影響因素包括主流道壓力分布，灌水器制造偏差及堵塞狀況等，但最主要因素是壓力分布[3]。若不考慮滴頭內部微流道幾何型式的差異，結合滴頭的自由出流特性，可不失一般性地認為滴頭所在位置的滴灌管主流道壓力水頭將全部轉化為滴頭內部微流道的沿程損失[4]。由Darcy-Weisbach沿程水頭損失公式可知，滴頭出流量與壓力水頭呈指數型關系[5]：=Cp。式中為滴頭流量，L/h；為滴頭安裝處滴灌管主流道的壓力值，MPa；和為滴頭的2個特性參數，分別稱為流量系數和流態指數。該式的合理性已被廣泛地證明，可見，滴頭出流量除了與自身特性參數、有關外，主要取決于壓力水頭的大小，故整個滴灌管路上的灌水均勻度主要取決于滴灌管主流道的沿程壓力分布。因此精確計算滴灌管路內的壓力分布是進行滴灌系統水力設計的前提條件，也是滴灌水力學研究的一個最基本問題。

國內外學者圍繞該問題進行了大量研究，Christiansen首先提出使用完整管計算水頭損失再折減計算多孔管水頭損失的多孔系數法，為多孔管路水頭損失的計算奠定了基礎。Wu等[6-8]隨后提出了能量坡度線法確定滴灌管路的沿程壓力水頭，使多孔管沿程壓力變化剖面大為簡化，并以此為基礎，發展了單一管徑條件下的變坡度計算方法。Jain等[9]利用已有經驗公式建立模型并對模型進行定性分析，并利用Darcy-Weisbach公式對滴灌管水頭損失進行了進一步計算分析得出其分布特點，所得結果接近實測但計算過程繁瑣，因而適用性較低。Kang等[10-12]采用有限元方法計算并總結繪制了滴灌管水力特性規律分布圖，同時分析了滴灌管沿程水頭損失的變化規律。

隨著滴灌技術的普及，直接針對滴灌管水力性能和簡化計算的研究越來越多，這些研究基本上不再基于適當的假設來進行解析，而是依賴試驗結果直接進行多因素系統的回歸分析[13-17]。另外，隨著數學建模方法和計算機技術的發展，相繼出現了一些利用新興算法，如二分法[18]、遺傳算法[19]、人工神經網絡[20]、CFD技術[21-23]等來研究滴灌管等多孔管路的能量損失及流動特性。

以上研究工作主要都是通過計算多孔管路的沿程水頭損失，來確定多孔管路的沿程壓力分布，即認為影響壓力分布的因素只有摩阻損失。但這種能量衡算法應用于滴灌管這類多孔管路計算時會產生2個問題：1）能量守恒定律是建立在總能量守恒基礎上的，而伯努利方程和水頭損失計算公式則均以單位質量進行計算，這對于和其他體系無質量交換的獨立流動體系是適用的。但在多孔管中，主流道流體流經側流孔口時，形成能量的重新分布，如果以主流道內單位質量的機械能進行總體能量衡算，則分流后的流體機械能必然大于分流前（若不考慮極短流程上的摩阻損失），這明顯違背了能量守恒定律，因此，單純地對主流道內流體應用能量方程不盡合理。2）恒定總流能量方程是由伯努利方程在過流斷面積分得來，而伯努利方程是按元流或流線建立的，對滴灌管這種多孔分流管，流體經過每個滴頭流出都有一條流線，即整個滴灌管路有多條非平行的流線，不同過流斷面處的流線數量不同。這意味著按照流線建立能量守恒方程和評估摩阻損失有多種可能。

滴灌管屬于多孔出流管，其中的流體在流動過程中質量不斷減少，屬于變質量流動，對于這種流動行為，可以采用動量分析方法進行研究。本研究采用質量和動量守恒原理，建立了以滴灌管為典型的變質量流動的數學模型，將主流道內的壓力變化歸結為動量交換和摩阻損失的雙重影響，并結合滴灌工程中常用的滴灌管結構參數和操作壓力進行了測壓-測流試驗，基于實測數據回歸得到了動量交換系數的變化規律，通過求解動量方程獲得了滴灌管沿程壓力分布的分析解，可為滴灌系統水力設計和校核提供依據，為變質量流動研究提供參考。

1 理論模型

1.1 變質量流動數學模型

滴灌管內流體的流動為變質量流動過程，可將滴灌管內的流動簡化為如圖所示的多孔出流，即等間距布孔且末端封閉的長直圓管，以管軸線為軸建立一維坐標，如圖1所示。在研究其流動行為時，假定滴灌管水平布置，且孔口排放壓力保持不變，即大氣壓力；主流流速在入口處最高，在封頭處等于0。

注：De為滴灌管內徑，m；s為側流孔口間距或滴頭間距，m。

在上述假定基礎上，各孔口流量分布將依賴軸線方向的壓力分布，在孔口前后取一微元段作為控制體，如圖2所示，根據質量和動量守恒定理，建立該變質量流動過程的基本方程組。

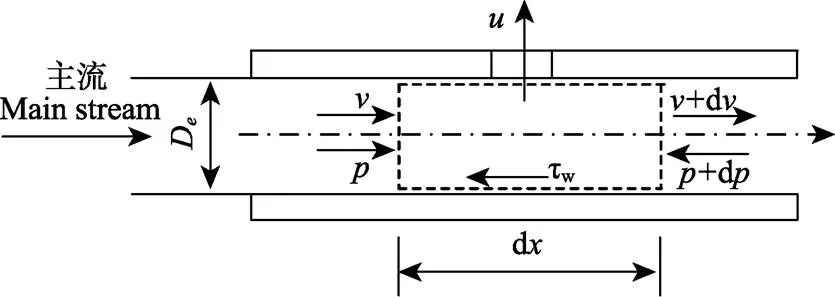
注：v為孔口前的流速，m·s-1；p為孔口前的壓力，Pa；u為孔口處的側向流速，m·s-1；tw為單位面積上管壁對控制體的摩阻力，N·m-2。

1）質量守恒方程

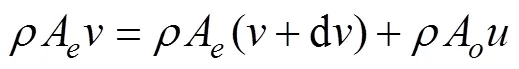
2）動量守恒方程

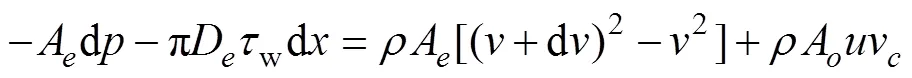
聯立方程（1）、（2）及圓管摩阻力公式w=(2/8)，并忽略d的高階項后得

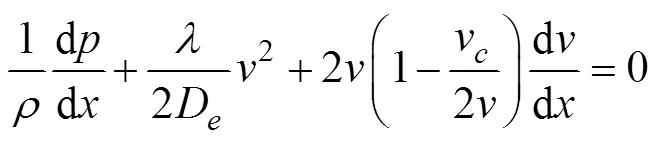
式中為水的密度kg/m3；A為滴灌管主流道過流斷面積，m2；A為側流孔口面積，m2；v為側流孔口出流帶走的軸向速度分量，m/s；為管壁摩阻系數。

由式（3）可見，軸向壓力變化取決于2項：2/2D表征管壁摩阻作用；(2-v)d/d表征動量輸運作用。引入修正系數，并令=1-c/2，表示對孔口出流帶走的軸向速度分量v的修正，稱為動量交換系數，則式（3）可寫為

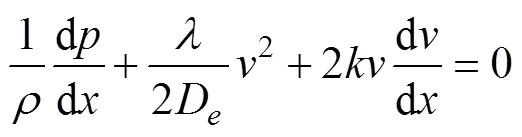
式（4）即為變質量流動行為的數學模型。

由于滴灌管主流道過流斷面上的速度分布是不均勻的，這種不均勻分布使得流體經過側流孔口流出時，并不嚴格垂直于軸線方向。采用動量交換系數的處理方法，其簡便之處在于不必考慮具體的流動細節，直接對側流孔口帶走的部分軸向動量分量進行修正，將模型簡化所引起的誤差都包含在這一修正系數中。

式（4）表明滴灌管主流道內的壓力變化受摩阻作用和動量交換的雙重影響，因此，壓力求解歸結為確定摩阻系數和動量交換系數，下面分而述之。

1.2 摩阻系數λ

尼古拉茲對內壁用人工加糙的圓管進行了深入的試驗研究，得出摩阻系數與管壁粗糙高度及雷諾數相關，并給出了各流態分區下摩阻系數隨二者的變化曲線。對于多孔管，其摩阻損失比同材質、同管徑及管長、同入口流量的完整管要小，工程計算中一般對完整管的摩阻系數進行折減后得到多孔管的平均摩阻系數，該折減系數稱為多孔系數[24]，常用的多孔系數表達式為Christiansen公式[13]

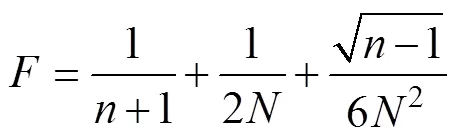
式中為Christiansen多孔系數；為流量指數，一般取1.75；為孔口或滴頭數目。

多孔系數法不考慮多孔管內的沿程變化，是一種平均化的簡化處理方法。本文所采用的變質量流動方程在推導時以分流口前后的微元體作為分析對象，引入的摩阻系數是指d管段上的實際摩阻系數值，與多孔管整體布孔數目無關，因此不需要以多孔系數法進行折減，而是采用隨軸向流速變化的連續函數進行表示（詳見3.1節），比多孔系數法更符合物理實際。根據尼古拉斯試驗結果，與管壁粗糙度、雷諾數有關，對于滴灌管來說，主流道的雷諾數不斷變化，流態逐漸發生轉捩，嚴格來說，應根據不同流態分區逐管段計算，但多項研究表明[25-29]，對于內徑小于80 mm的PE材質滴灌管，全管路統一按照紊流光滑區處理時具有足夠計算精度，即滴灌管摩阻系數計算時采用Blasius阻力公式

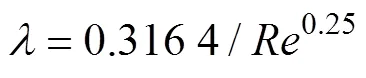
式中雷諾數=vD/μ為水的運動黏度。

1.3 動量交換系數k

動量交換系數是求解變質量流動數學模型的關鍵。將式（4）在主流道的任意2截面至間積分，可得

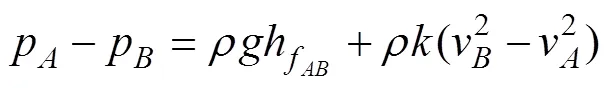
即

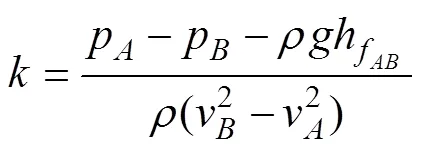
式中p、p分別為、2測點的壓力；v、v分別為、2測點的軸向流速，m/s；h為、2測點之間的摩阻水頭損失，m；為重力加速度，取9.8 m/s2。

式（8）即對動量交換系數進行試驗測定的原理式。通過室內測壓試驗數據回歸可確定的經驗表達式，并用于變質量流動數學模型求解。首先，需要定性分析的物理意義及影響因素，確定其函數形式。

1）隨管路坐標位置的變化

方程推導過程表明，動量交換系數的作用是對側流孔口帶走部分軸向動量分量進行修正，即孔口前后主流速的變化是由孔口出流帶走的軸向分量引起，也就是孔口出流帶走的流體動量的軸向分量應是主流動量（或動能）變化的分數，即

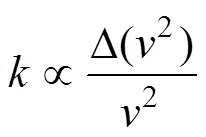
由以上分析可知，相對動能差的數學表達式成為推求值函數形式的關鍵。由數學分析

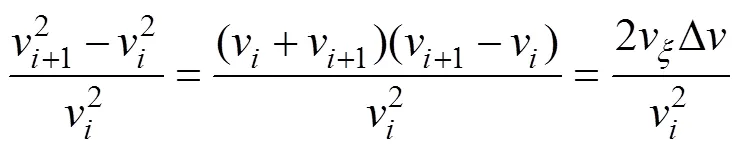
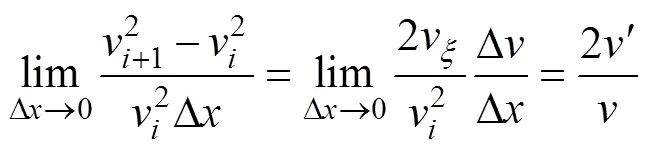
即

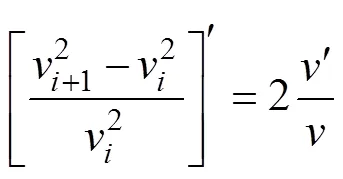
對式（11）從0到積分，得到相對動能差的函數式

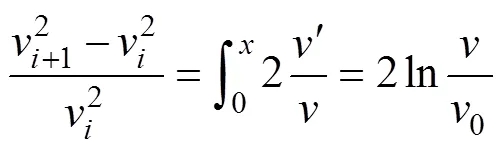
式中0為滴灌管入口流速，m/s。

聯立式（9）和（13），得到

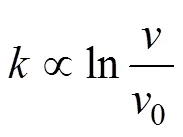
由式（14）可以確定，與管路軸向流速分布有關，滴灌管的軸向流速分布為階梯型的分段函數，為了方便數學處理，本文將滴灌管主流道的軸向流速分布簡化為連續函數，并假定具有以下指數分布形式

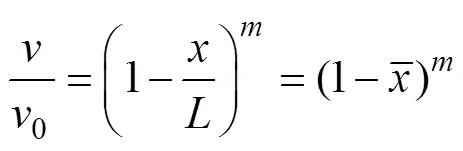
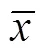
結合式（14）、（15），可知

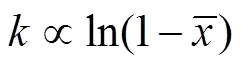
可見是隨管路坐標位置發生變化的。

2）隨滴灌管結構參數的變化

在變質量流動的方程推導過程中，分析對象為主流道過流面積沿程不變的多孔管路，但對于內鑲式滴灌管，由于圓柱形滴頭的鑲入，滴頭安裝處的主流道過流面積先縮小、后擴大，如圖3所示。流體流經該處時，因慣性作用，主流與邊壁分離，并在分離區產生漩渦，在漩渦區內部，水體擾動加劇，同時主流與漩渦區之間不斷進行質量及動量交換，引起局部能量損失及流速分布的重新調整，經側流孔口所帶走的軸向速度分量必然受到影響。作為衡算該軸向速度分量的修正系數，也必然發生變化，其變化情況取決于邊界變化的劇烈程度。

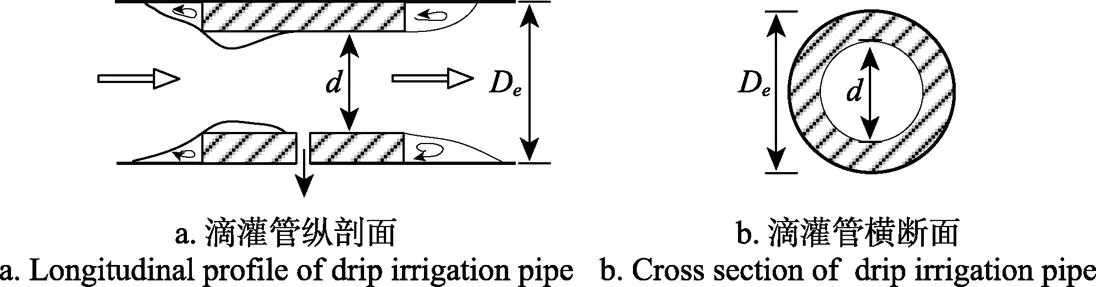
注：d為圓柱形滴頭的內徑，m。

滴灌管內徑D對應的過流面積為A，圓柱形內鑲滴頭的內徑對應的過流面積為A，定義=A/A為斷面收縮比，以此表征滴頭安裝處過流面積變化的劇烈程度。由以上分析可知，是斷面收縮比的函數。

綜上，在內鑲式滴灌管中，動量交換系數受管路坐標位置和斷面收縮比的影響。結合式（16），并便于數據回歸時線性化處理，設具有如下函數形式

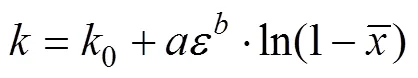
式中0為試驗測得的的最大值；、均為待定參數。

1.4 沿程壓力分布

變質量流動數學模型表明，多孔管壓力變化值取決于摩阻系數和動量交換系數，在以上的分析和推導過程中，已經確定了和的函數表達式，因此，可以進行變質量流動數學模型的求解，將表達式（6）、表達式（17）和滴灌管軸向流速分布式（15），代入變質量流動方程式（4），得

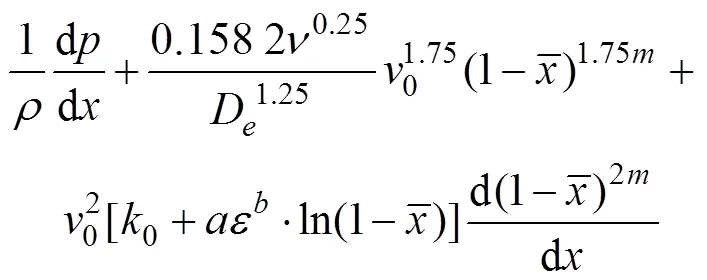
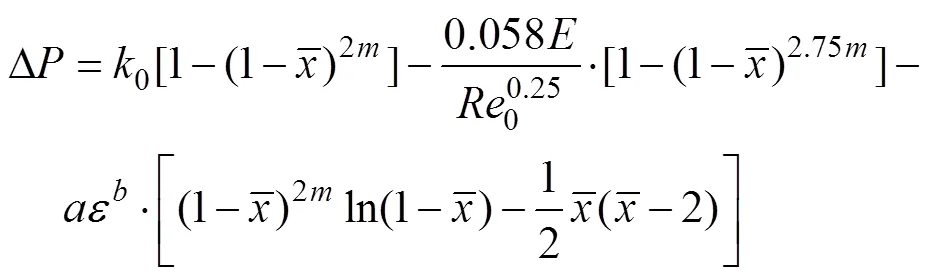
式中=/D為滴灌管長徑比；0=0D/為滴灌管的管首雷諾數。

式（19）中尚包含4個待定參數：0、、和流速分布指數。需通過滴灌管沿程測壓-測流試驗，確定這4個待定參數，以獲得完善的沿程壓力分布解。

2 室內測壓試驗

2.1 試驗材料

供試的6種內鑲式滴灌管（陜西省楊凌秦川節水灌溉公司提供），分別以A、B、C、D、E、F表示，表1中給出了6種滴灌管的基本特性參數。

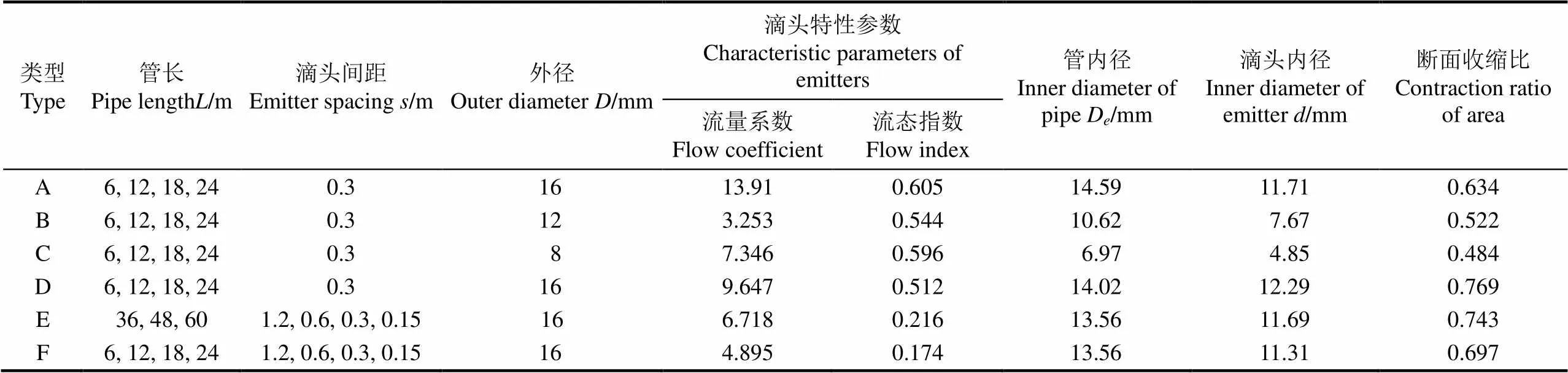
表1 供試滴灌管的基本參數

2.2 試驗裝置與方法

試驗裝置主要由蓄水箱、離心泵、恒壓變頻柜、精密壓力表、滴灌管、閘閥、試驗臺、壓差計、燒杯、集水槽、稱質量設備等組成。試驗中的主要變化參數包括滴灌管種類（6種）、滴頭間距、滴灌管總長度和首部壓力水頭0，其中滴灌管種類、滴頭間距、滴灌管總長度的水平設定在表1中已經列出，首部壓力0通過恒壓變頻柜設置0.02，0.04，0.06，0.08，0.10，0.12 MPa共6個水平。滴灌管測壓-測流裝置如圖4所示。對于每組量測工況，首先將待測滴灌管水平順直鋪設，末端封堵，在滴灌管入口處接入精密壓力表，打開水泵，通過調節變頻柜設定所需的首部壓力，待水流運行平穩后，開始測壓及測流，試驗過程中蓄水箱水溫維持在20 ℃左右（水的運動黏度取=10-6m2/s）。每組工況通過更換管道設置3個有效重復。

測壓-測流試驗的目的是回歸得到流速分布指數和經驗表達式中的待定參數0、、，以及對壓力分布模型進行驗證。

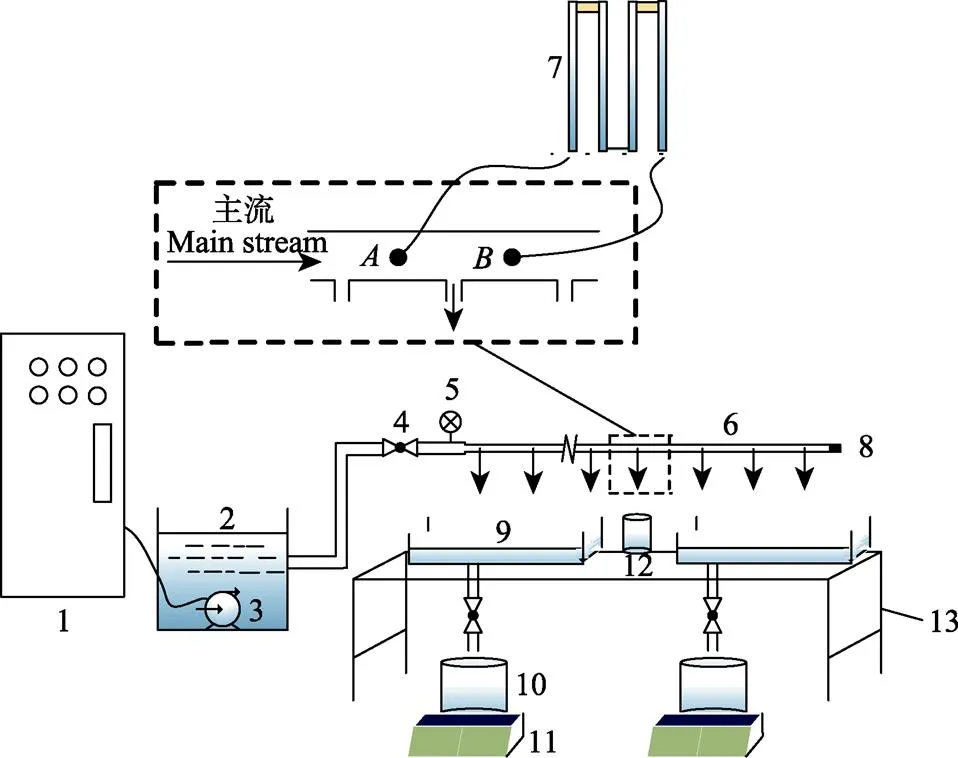
1. 變頻柜 2. 蓄水箱 3. 離心泵 4. 球閥 5. 壓力表 6. 滴灌管 7. 壓差計 8. 堵頭 9. 集水槽 10. 水桶 11. 電子秤12. 量杯 13. 試驗臺

3 結果與分析

3.1 主流道軸向流速分布

滴灌管主流道軸向流速分布歸結為對流速分布指數的回歸，在以上的分析中，已經包含了對滴灌管結構參數（長徑比）和流動參數（管首雷諾數0）的考慮，其他因素中，流速分布的形式可能與滴頭的自身特性參數（流量系數、流態指數）及滴頭安裝個數有關。

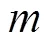
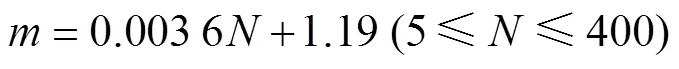
根據式（20），式（15）可寫為

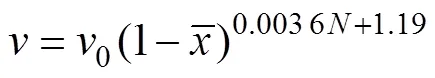
此即基于試驗實測得到的滴灌管軸向流速分布公式，圖6為由式（21）計算得到的不同滴頭安裝個數條件下的滴灌管軸向流速變化規律。橫坐標為滴灌管路相對位置，即。

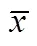
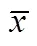
圖6 不同滴頭個數時的軸向流速分布

Fig.6 Relationship between number of emitters and axial velocity profile

3.2 動量交換系數回歸

由測壓-測流試驗數據，計算得到不同工況條件、不同管路位置處的動量交換系數。

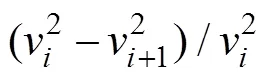
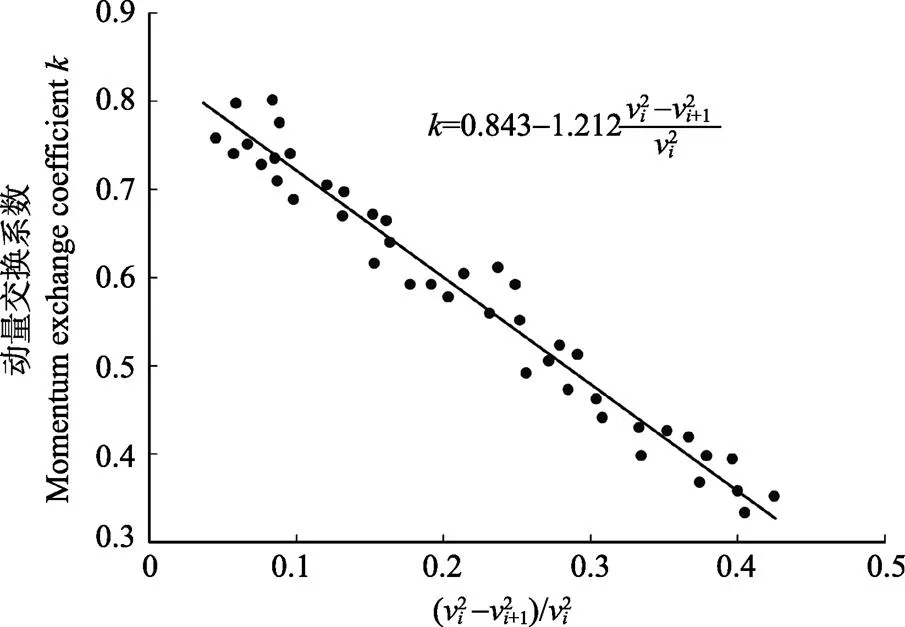
圖7 滴灌管A中動量交換系數k與的關系

對按照式（17）進行數據回歸，結果如下

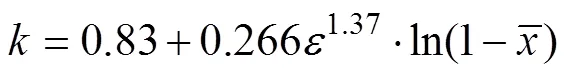
根據式（22）繪出6種供試滴灌管的動量交換系數k的沿程變化規律，如圖8所示。若將式（8）代入恒定總流能量方程，可得k=0.5，故應用能量方程求解多孔管流動，可以看作是一種特殊的動量方程解法，只是動量交換系數取常數0.5，未考慮k的沿程變化。由于滴灌管沿程泄流，主流道內的水動力特性沿程不斷變化，孔口處的動量交換作用也必然發生變化，因此，相較于能量方程法，考慮k沿程變化的動量方程法更符合物理真實。

3.3 滴灌管主流道沿程壓力分布模型及驗證

由前面的推導公式和3.1、3.2節的實測回歸結果，聯立式（19）、（20）和（22）得到滴灌管沿程壓力分布的完整理論計算式

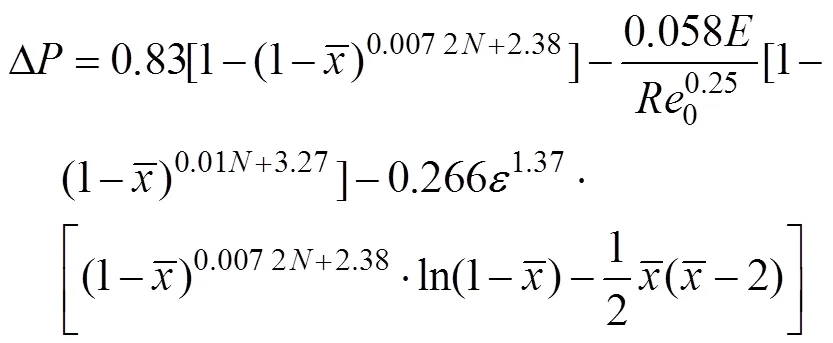
式（23）即根據變質量流動的數學方程，由滴灌管測壓-測流試驗數據回歸得到的無量綱形式的滴灌管沿程壓力分布模型。

圖9給出了5種典型工況下滴灌管沿程壓力分布的實測值與式（23）計算值的對比。由圖9可見，計算結果與實測結果吻合較好，通過對比試驗所有工況的實測值與模型計算值，得到沿程壓力的最大相對誤差為4.27%，表明式（23）用于滴灌管沿程壓力分布具有一定的精確性。因此，動量方程方法用于求解變質量流動行為，具有一定的合理性。

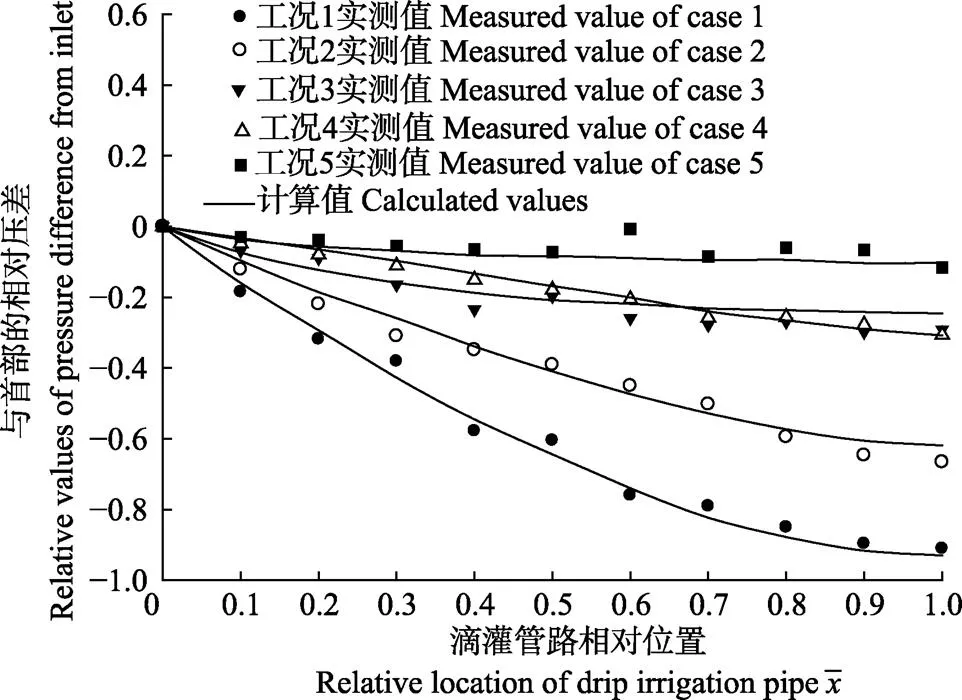
注：工況1：管E，H0=0.12 MPa，N=400；工況2：管A，H0=0.10 MPa，N=80；工況3：管D，H0=0.08 MPa，N=60；工況4：管C，H0=0.10 MPa，N=80；工況5：管B，H0=0.04 MPa，N=40。

4 結論與討論

以質量和動量守恒定理為依據，建立了以滴灌管為典型的變質量流動數學模型，結合室內測壓試驗分析了滴灌管主流道的流動行為，并基于實測數據獲得了滴灌管主流道內沿程壓力分布的分析解。本研究主要獲得了以下結論：

1）分析了能量方程應用于滴灌管水力計算的局限性，并基于動量定理建立了變質量流動數學模型，動量方程表明：滴灌管主流道壓力變化取決于摩阻項和動量交換項2個部分，沿程壓力分布的具體形式取決于二者作用的相對強弱。動量方程建立的合理之處在于更加符合流動真實，物理意義更加明晰，簡便之處在于不必追究其詳細機制，將復雜的流動機理進行了合理概化。

2）對軸向流速分布指數進行了方差分析，結果表明，軸向流速分布指數與滴頭自身特性參數無關，而與滴頭安裝個數呈線性相關關系，回歸的到了滴灌管軸向流速分布公式。

3）定性分析了動量交換系數的影響因素，確定了其由斷面收縮比和管路相對位置構成的函數形式，并基于試驗數據回歸得到滴灌管動量交換系數的經驗表達式。

4）結合摩阻系數的Blasius公式和動量交換系數的經驗表達式，求解動量方程，獲得了滴灌管的沿程壓力分布模型。通過對比試驗工況的實測值與模型計算值，得到沿程壓力的最大相對誤差為4.27%。

本文為滴灌管等多孔管路計算提供了一種思路，但所得的壓力分布模型不夠簡潔，其實用性有待提高。今后的研究工作應深入對流動機理的研究，進一步完善多孔管路的水動力學模型，尤其需要更加廣泛地測定相關參數，簡化沿程壓力分布模型，提高實用性，從而便捷地為滴灌系統的設計、運行和校核提供科學依據。

[1] 范軍亮，張富倉，吳立峰，等. 滴灌壓差施肥系統灌水與施肥均勻性綜合評價[J]. 農業工程學報，2016，32(12)：96－101.

Fan Junliang, Zhang Fucang, Wu Lifeng, et al. Field evaluation of fertigation uniformity in drip irrigation system with pressure differential tank[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 96－101. (in Chinese with English abstract)

[2] 朱德蘭，張林. 基于流量偏差率的滴灌毛管管徑簡易設計[J]. 農業工程學報，2016，32(5)：14－20.

Zhu Delan, Zhang Lin. Simplified method for designing diameter of drip irrigation laterals based on emitter flow variation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(5): 14－20. (in Chinese with English abstract)

[3] 張林，范興科，吳普特，等. 均勻坡度下考慮三偏差的滴灌系統流量偏差率的計算[J]. 農業工程學報，2009，25(4)：7－14.

Zhang Lin, Fan Xingke, Wu Pute, et al. Calculation of flow deviation rate of drip irrigation system taking three deviation rates into account on uniform slopes[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(4): 7－14. (in Chinese with English abstract)

[4] 田濟揚，白丹，任長江，等. 滴灌雙向流流道灌水器水力特性分析[J].農業工程學報，2013，29(20)：89－94.

Tian Jiyang, Bai Dan, Ren Changjiang, et al. Analysis on hydraulic performance of bidirectional flow channel of drip irrigation emitter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(20): 89－94. (in Chinese with English abstract)

[5] 劉楊，黃修橋，馮俊杰，等. 地下滴灌毛管水頭偏差率特性及與土壤水分均勻度的關系[J]. 農業工程學報，2017，33(14)：108－114.

Liu Yang, Huang Xiuqiao, Feng Junjie, et al. Head deviation property and its relationship with soil moisture uniformity of subsurface drip irrigation laterals[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(14): 108－114. (in Chinese with English abstract)

[6] Wu I P, Gitlin H M. Design of irrigation lines[J]. Technical Bulletin of the University of Hawaii, 1974, 96(1): 3－29.

[7] Wu I P, Gitlin H M. Drip irrigation design based on uniformity[J]. Transactions of the ASAE, 1974, 17(3): 429－432.

[8] Wu I P. A uni-plot for drip irrigation lateral and submain design[J]. Transactions of the ASAE, 1985, 28(2): 522－528.

[9] Jain S K, Singh K K, Singh R P, et al. Micro-irrigation lateral design using lateral discharge equation[J]. Journal of Irrigation and Drainage Engineering, 2002, 128(2): 125－128.

[10] Kang Y H, Nishiyam A S. Design of micro-irrigation sub-main units[J]. ASCE. Journal of Irrigation and Drainage Engineering, 1996, 122(2): 83－89.

[11] Kang Y H, Nishiyama S. Hydraulic analysis of microirrigation submain nuits[J]. Transactions of the ASAE, 1995, 38(5): 1377－1384.

[12] Kang Y H, Nishiyama S. A simplified method for design of microirrigation laterals[J]. Transactions of the ASAE, 1996, 39(5): 1681－1687.

[13] Demir V, Yurdem H, Degirmencioglu A, et al. Development of prediction models for friction losses in drip irrigation laterals equipped with integrated in-line and on-line emitters using dimensional analysis[J]. Bio-systems Engineering, 2007, 96(4): 617－631.

[14] Wang Y, Zhu D, Lin Z. Dimensional analysis for estimating the local head losses in trickle laterals equipped with integrated in-line emitters[J]. Journal of Hydraulic Engineering, 2015, 46(5):602－611.

[15] Gomes A W A, Frizzone J A, Rettore Neto O, et al. Local head losses for integrated drippers in polyethylene pipes[J]. Engenharia Agrícola, 2010, 30(3): 435－446.

[16] Zitterell D B, Frizzone J A, Neto O R. Dimensional analysis approach to estimate local head losses in microirrigation connectors[J]. Irrigation Science, 2014, 32(3): 169－179.

[17] Sadeghi S H, Peters R T, Lamm F R. Design of zero slope microirrigation laterals: Effect of the friction factor variation [J]. Journal of Irrigation & Drainage Engineering, 2015, 141(10): 04015012.

[18] 王新坤. 基于二分法的微灌毛管水力設計[J]. 排灌機械工程學報，2007，25(6)：27－30.

Wang Xinkun. Hydraulic design of micro-irrigation laterals based on bisection method[J]. Drainage and Irrigation Machinery, 2007, 25(6): 27－30. (in Chinese with English abstract)

[19] 白丹，王新. 基于遺傳算法的多孔變徑管優化設計[J]. 農業工程學報，2005，21(2)：42－45.

Bai Dan, Wang Xin. Optimum design for tapered diameter pipeline with multiple outlets based on genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(2): 42－45. (in Chinese with English abstract)

[20] Martí P, Provenzano G, Royuela á, et al. Integrated emitter local loss prediction using artificial neural networks[J]. Journal of Irrigation & Drainage Engineering, 2010, 136(1): 11－22.

[21] Provenzano G, Dio P D, Salvador G P. New computational fluid dynamic procedure to estimate friction and local losses in coextruded drip laterals[J]. Journal of Irrigation and Drainage Engineering, 2007, 133(6): 520－527.

[22] 王福軍，王文娥. 滴頭流道CFD分析的研究進展與問題[J]. 農業工程學報，2006，22(7)：188－192.

Wang Fujun, Wang Wen’e. Research progress in analysis of flow passage in irrigation emitters using computational fluid dynamics techniques[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(7): 188－192. (in Chinese with English abstract)

[23] 田濟揚，白丹，于福亮，等. 基于Fluent軟件的滴灌雙向流流道灌水器水力性能數值模擬[J]. 農業工程學報，2014，30(20)：65－71.

Tian Jiyang, Bai Dan, Yu Fuliang, et al. Numerical simulation of hydraulic performance on bidirectional flow channel of drip irrigation emitter using Fluent[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(20): 65－71. (in Chinese with English abstract)

[24] 張國祥. 多孔系數的一個近似計算公式[J]. 排灌機械工程學報，1983(2)：35－37.

[25] Bernuth R D V, Wilson T. Friction factors for small diameter plastic pipes[J]. Journal of Hydraulic Engineering, 1989, 115(2): 183－192.

[26] Bagarello V, Ferro V, Provenzano G, et al. Evaluating pressure losses in drip-irrigation lines[J]. Journal of Irrigation & Drainage Engineering, 1997, 123(1): 1－7.

[27] Losada A, Juana L, Rodr? Guezsinobas L. Determining minor head losses in drip irrigation laterals. I: Methodology [J]. Journal of Irrigation & Drainage Engineering, 2002, 128(6): 376－384.

[28] Provenzano G, Pumo D. Closure to “Experimental analysis of local pressure losses for microirrigation laterals” by Giuseppe Provenzano and Domenico Pumo[J]. Journal of Irrigation & Drainage Engineering, 2006, 132(2): 189－193.

[29] Yildirim G. Total energy loss assessment for trickle lateral lines equipped with integrated in-line and on-line emitters[J]. Irrigation Science, 2010, 28(4): 341－352.

Modelling and verification of pressure distribution along mainstream in drip irrigation pipe

Ding Falong1, Mao Zeyu1, Wang Wen’e2, Han Kai1

(1.,,100084,; 2.,712100,)

Irrigation uniformity is the core evaluation index of drip irrigation. The influence factors of irrigation uniformity include pressure along mainstream way, emitter manufacturing deviation and emitter clogging, etc., but the leading factor is the longitudinal pressure distribution. Therefore, calculation of pressure is prerequisite for hydraulic design of drip irrigation system, and it is also the most basic problem for the study of drip irrigation hydraulics. Scholars at home and abroad have done a lot of research on this problem. According to the author's references, all the past research results were based on the energy conservation law, researchers mainly calculated the frictional head loss to determine the pressure distribution along drip irrigation pipe, and the friction resistance was the default for the only factor affecting the pressure distribution. However, this method neglects the energy of the fluid flowing through sidewards orifices, and it is not completely applicable to the drip irrigation pipe. To reveal the behavior of variable mass flow, and simplify the hydraulic calculation of drip irrigation pipe, this study established the basic equation of variable mass flow based on mass conservation and momentum conservation theories, and thus developed an analytical model of pressure distribution along mainstream in drip irrigation pipe. Momentum equation of variable mass flow is clearer in physical meaning, and it does not require to investigate the complex flow mechanism in detail, but rather rationally simplify uncertain factors. The developed model shows longitudinal pressure profile in drip irrigation pipe is determined by the friction loss and the momentum exchange, the friction loss tends to decrease the pressure while the momentum exchange just the opposite. The solution of pressure in mainstream way is attributed to determination of friction coefficient and momentum exchange factor. The friction coefficient of drip irrigation pipes could be determined by Blasius resistance formula, according to many existing research conclusions. Function form of momentum exchange factor was qualitatively analyzed, and it was represented by area contraction ratio caused by in-line emitters and relative axial location. A series of indoor pressure tests were performed on 6 types of drip irrigation pipes with different lengths, different emitter spaces and different operating pressures. According to the test result, axial velocity distribution index was obtained by regression, and variance analysis of 2 factors was performed, 2 possible influencing factors were emitter type and number of emitters. Variance analysis results showed that at a significance level of 5%, emitter types did not have a significant impact on axial velocity distribution index, meaning that with the condition of same number of emitters, axial velocity distribution indexes of different emitter types had no significant statistical differences. However, test results showed axial velocity distribution index was linearly dependent on number of emitters. Empirical expression of momentum exchange factor was regressed. Combined with the Blasius formula, the momentum equation of variable mass flow was solved, and pressure distribution along main stream in drip irrigation pipe was obtained. Calculated values of longitudinal pressure agreed well with measured values among all cases, and the maximum relative error was 4.27%. Although drip irrigation has been widely applied, research of flow characteristics in drip irrigation pipe is still inadequate, corresponding hydraulic calculations tend to mechanically adopt old methods, regardless of the applicability. This study offers a idea for hydraulic calculation of drip irrigation, the results will provide scientific evidence not only for structural and operational optimization of drip irrigation, but also for hydrodynamics study of multiple outlet pipes. What needs to be improved is the obtained pressure distribution model is not simple enough, so further research should perfect the flow mechanism, and measure relevant parameters more widely to simplify the current model.

irrigation; models; pressure; mainstream way; flow of variable mass; friction resistance; momentum exchange

丁法龍，茅澤育，王文娥，韓 凱. 滴灌管主流道沿程壓力分布模型及驗證[J]. 農業工程學報，2019，35(3)：117－124. doi：10.11975/j.issn.1002-6819.2019.03.015 http://www.tcsae.org

Ding Falong, Mao Zeyu, Wang Wen’e, Han Kai. Modelling and verification of pressure distribution along mainstream in drip irrigation pipe[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(3): 117－124. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.03.015 http://www.tcsae.org

2018-07-05

2018-12-30

國家重點研發計劃（2016YFC0402504）

丁法龍，博士生，主要從事水力學及河流動力學方面的研究工作。Email：dflaizy@163.com

10.11975/j.issn.1002-6819.2019.03.015

S275.6

A

1002-6819(2019)-03-0015-08