帶有卷積非線性項的Kirchhoff方程解的多重性

耿 茜，李宇華

（山西大學數學科學學院，太原 030006）

本文主要考慮的是下列帶有卷積非線性項的Kirchhoff方程：

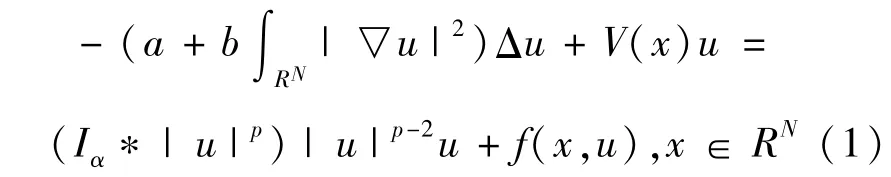
這里a，b＞0。N是給定歐氏空間RN的空間維數。對于任給的 x∈RN＼｛0｝，α∈（0，N），Riesz勢函數Iα∶RN＼｛0｝→R定義如下：

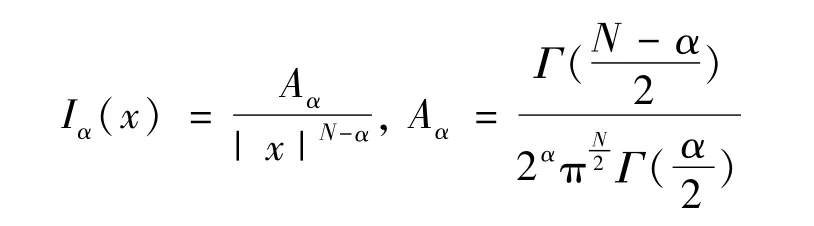
在 a＝1，b＝0，N＝3，α＝2，p＝2以及 f＝0的情形下，方程（1）轉化為下列著名的 Choquard-Pekar方程：

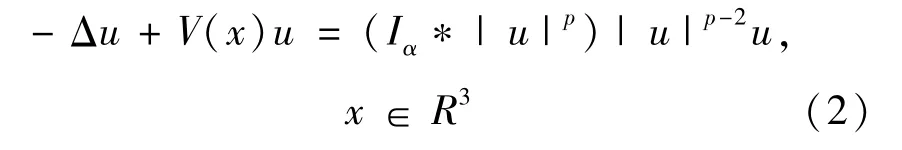
這類方程有著豐富的物理背景。例如，在文獻［1］中，Pekar用此方程的駐波解來描述量子力學中極化子的靜態現象。Choquard用它來模擬電子俘獲現象以及在經典引力勢中耦合的 Schr?dinger方程。更多具體成果可以參考文獻［2-4］。近幾十年來，關于方程（2）解的存在性及其定量性質有著豐富的研究成果。當V＝1時，E.H.Lieb首次在文獻［5］中考慮了方程（2）正解的存在性以及唯一性。P-L.Lions在文獻［6-7］中得到了正規化解的存在性與多重性。當V是正常數時，V.Moroz和J.Van Schaftingen在文獻［8-10］中建立了問題（2）基態解的存在性。然而，之前關于Kirchhoff方程非線性項的研究通常都是多項式的形式，針對帶有卷積非線性項的Kirchhoff問題的探索較少。由于 （∫RN｜▽u｜2）Δu的存在，方程（1）不再是逐點成立的等式，這無疑增加了問題的難度。本文的主要目的：首先，克服非局部項與卷積非線性項之間的相互干擾；其次，解決由于兩項非線性項次數的不同在利用Fountain定理時產生的困難；最后，探究方程（1）的解是否具有多重性。由于卷積非線性項與通常的多項式非線性項不同，本文在研究方法上有了一定的創新。

（f1）f∈C（RN×R，R）且對于任意的 u∈R，x∈RN，均存在常數 C1＞0，q∈（2，2*）使得

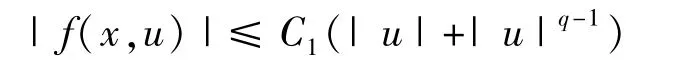
（f2）當｜u｜→0時，f（x，u）＝o（｜u｜）關于 x∈RN一致成立。

（f3）存在 θ＞4使得對任給的 x∈RN，u∈R＼｛0｝均有 0＜θF（x，u）≤uf（x，u）。

（f4）對于任意的 x∈RN，u∈R＼｛0｝滿足f（x，-u）＝-f（x，u）。

主要結果如下：

定理1 假設條件（f1）-（f4）成立，V∈C（RN，［0，＋∞）），如 果 p∈而 且（x）＞0，｜xl｜i→m∞V（x）＝＋∞。則方程（1）具有一個無界的高能量解序列。

1 預備工作

首先給出Hilbert空間：

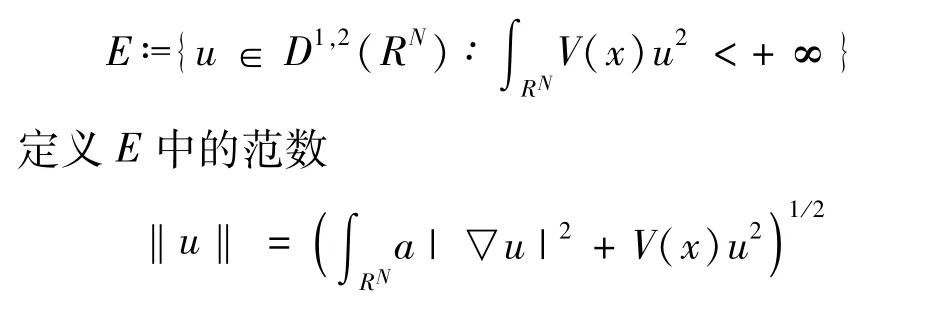
由定理1中關于勢函數V的假設，文獻［11］證明了 E緊嵌入到 Lr（RN），r∈［2，6）。設｛en｝是特征問題-aΔu＋V（x）u＝λu的特征函數，那么 λ1＝‖u‖2＞0。容易證明對應于不同特征值的特征函數在L2（RN）中是正交的。又因為對任何的 ei，ej，i≠j，都有（ei，ej）＝λi（ei，ej）2＝0。所以｛ei｝在 E中是正交的。不妨假設｜｜en｜｜＝1，n∈N。設 u∈E，而且（en，u）＝0，n∈N，則從（en，u）＝λn（en，u）2推出（en，u）2＝0，n∈N，而且 u＝0，因此｛en｝是 E中的一組基。設 En＝Ren，n∈N，則令

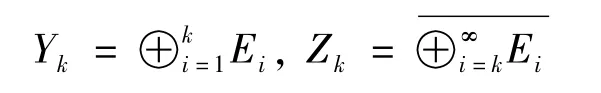
在E中定義方程（1）的能量泛函J∶E→R

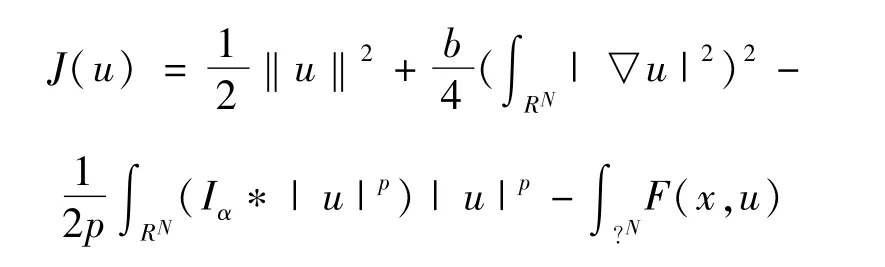
本文不同行之間 C、C1、C2、C3、Cε定義可能為不相同的正常數。｜·｜p表示通常的 Lp（RN）中的范數，（·，·）2表示 L2（RN）中對應的內積。為了建立變分結構，具體給出下列 Hardy-Littlewood-Sobolev不等式，而且根據Hardy-Littlewood-Sobolev不等式以及Nemystkii算子可知能量泛函J定義是合理的，一階連續可微的。

2 主要引理

引理 1［12］假設 t，r＞1，f∈Lt（RN），h∈Lr（RN）滿足1／t＋1／r＋（N-α）／N＝2。則存在正常數C與f、h無關，使得

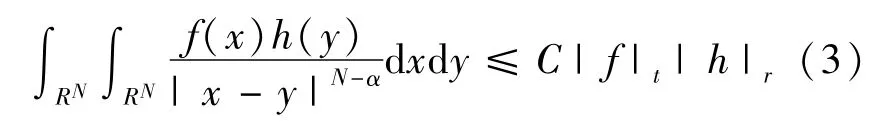
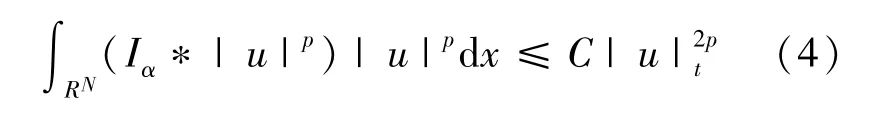
引理2 如果 p∈［2，2*），k→ ＋∞，則 βksupu∈Zk，‖u‖＝1｜u。

證明 因為 0＜βk＋1≤βk，所以 βk→β≥0。又對每一個 k∈N，存在 uk∈Zk，｜｜uk｜｜＝1使得｜uk｜p＞βk／2。根據 Zk的定義，在 E中 uk?0。于是，根據 Sobolev嵌入定理，在 Lp（RN）中 uk→0。因此，β＝0。

引理3［13］設 J∈C1（E，R）滿足 J（-u）＝J（u），并且對于任意的 k∈N，存在 ρk＞γk＞0使得：

（A1）ak（u）≤0；（A2）當 k→時，bk（u）→ ＋∞；（A3）對任意的c＞0，J均滿足（PS）c條件，則 J具有一列無界的臨界值。

引理4 假設定理1的條件成立，對任意的c＞0，J均滿足（PS）c條件。

證明 任給c＞0，假設｛un｝是能量泛函J的一個（PS）c序列，即當n→∞時

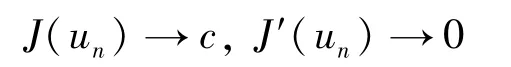
則｛un｝在E上有界。事實上，由條件（f3）可知

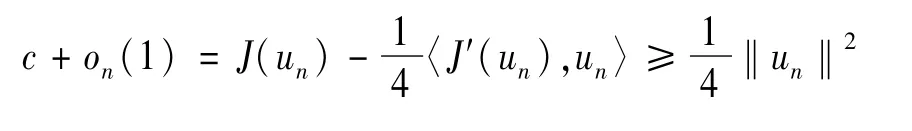
因此得到｛un｝的子列仍記作｛un｝，在 E上滿足un?u。文獻［14］借助于Stein-Weiss不等式和半群等式得到 Riesz勢函數 Iα＝Iα／2*Iα／2。則

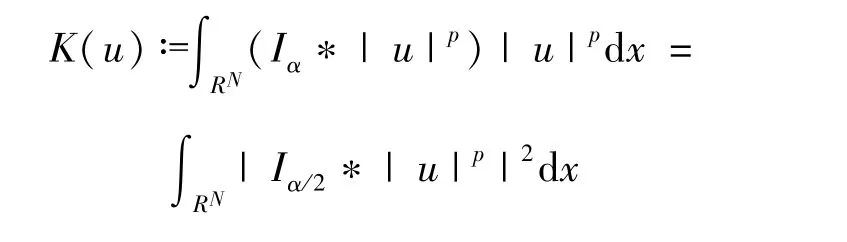
通過文獻［15］Proposition 2.2可知 K′：E→E*是弱連續的。從而

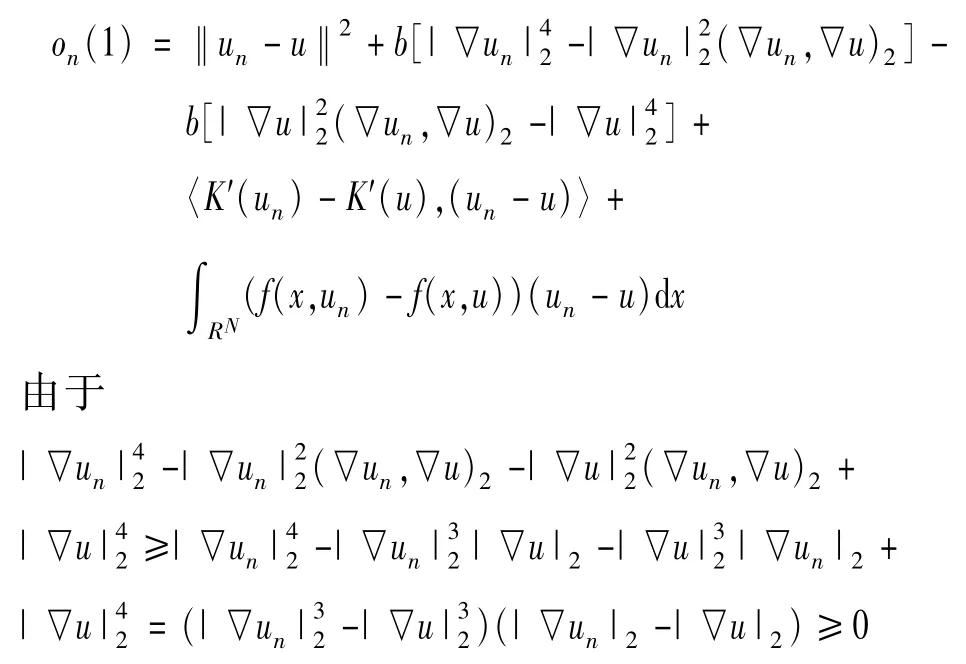
而且根據條件（f1）、（f2）以及 H?lder不等式有

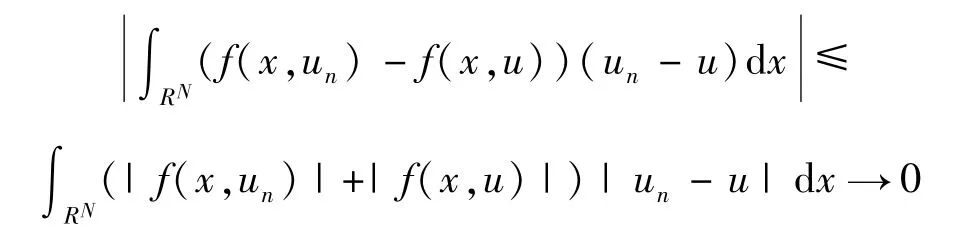
因此當n→∞時，‖un-u‖→0。

3 定理1的證明

證明 當 u∈Yk，根據條件（f2）～（f4），任給x∈RN，u∈R，存在常數 C2＞0，C3＞0，使得

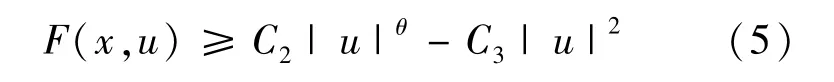
根據式（5）可得

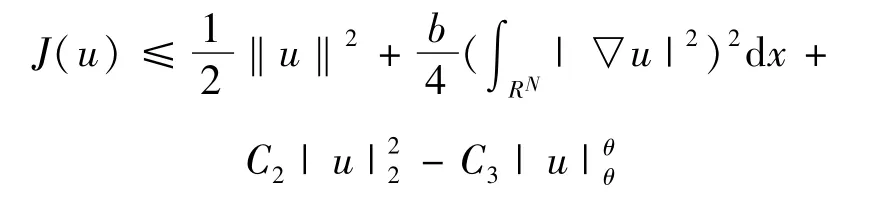
由于Yk是有限維空間，進而Yk上的范數是等價的。因此，存在 ρk＞γk＞0。使得當‖u‖ ＝ρk，ρk充分大時條件（A1）成立。

當 u∈Zk，根據條件（f1）、（f2）可知對于任意的 ε＞0，存在 Cε＞0，使得

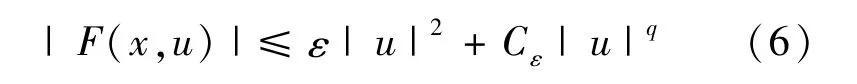
再根據引理2可知當k→＋∞時，βk→0。而且

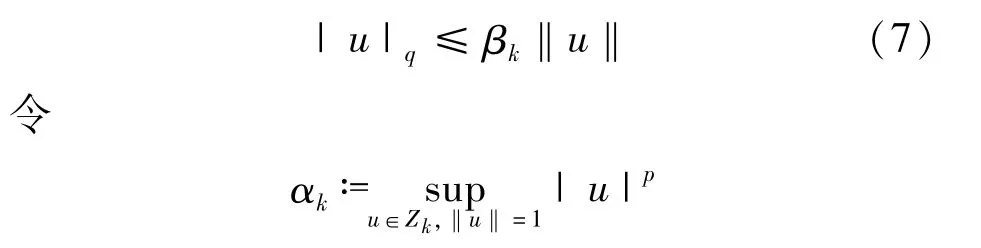
同理由引理2可知，如果 p∈［2，2*），k→ ＋∞，則αk→0。且

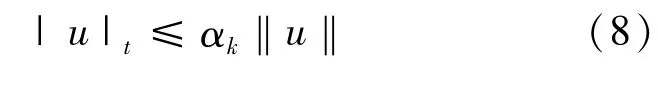
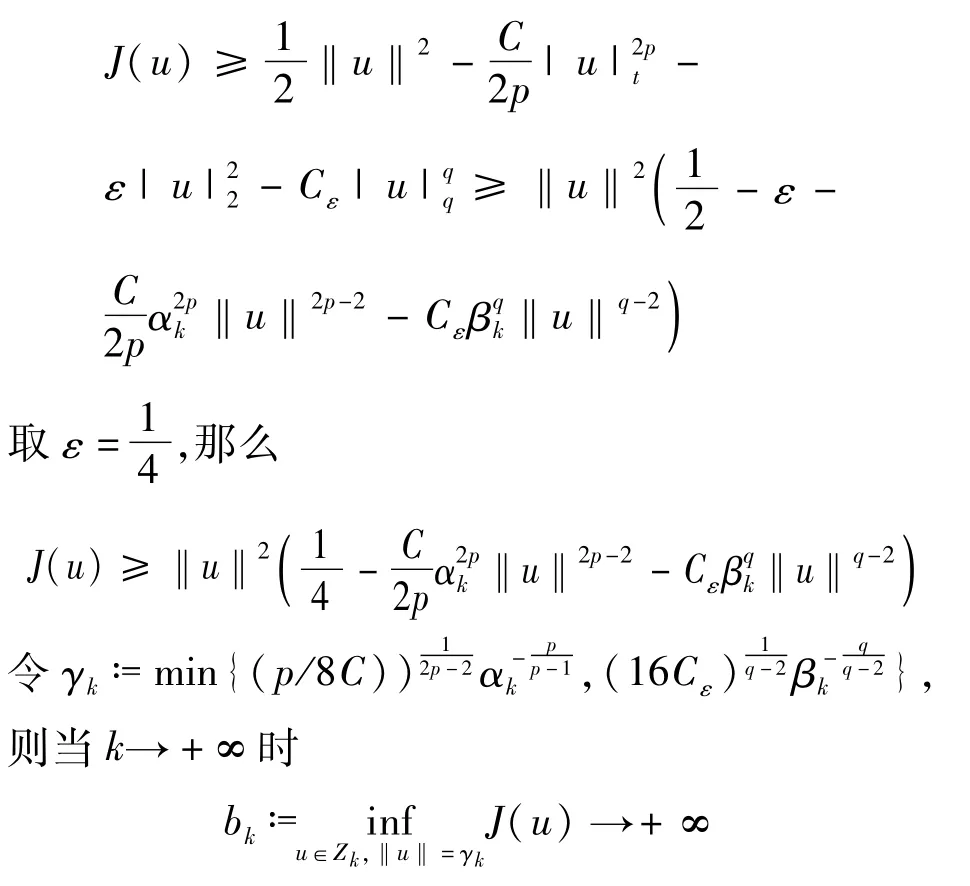
于是條件（A2）成立，所以根據引理3可知結論成立。