基于ARMA模型的地鐵站環控系統能耗預測

(1 華中科技大學能源與動力工程學院 武漢 430074； 2 廣州市地下鐵道總公司 廣州 510030)

隨著近年城市化進程的推進，我國城市軌道交通得到了大力發展。截至2016年，我國已有29座城市開通軌道交通運營線路，運營總線路達130條，總里程達3 849 km。由于具有節約地面空間、噪音低、采用清潔能源減少污染等特性，地鐵逐漸成為城市和區域的軌道交通主力。作為城市軌道交通主干網，地鐵成為城市能源消耗的重要組成部分，其中地鐵站環控系統(HVAC系統，供熱通風和空調系統)的能耗占比較大[1-2]。Wang Yongcai等[3]通過對北京地鐵站環控系統能耗的分析指出，2012年北京地鐵站環控系統總能耗在夏季每月可達1.819×107kW·h。朱穎心等[4-5]指出在地鐵運行期間，北京地鐵站環控系統能耗與列車的牽引能耗相當。建立有效的地鐵站環控系統能耗預測模型，實時對地鐵站環控系統能耗做出預測和分析，從而對環控系統進行實時運行調節，一方面可以提高環控系統運行效率，保障機組的高效運行，另一方面可以降低地鐵站的能耗。因此，建立有效的地鐵環控系統能耗預測模型對于地鐵站節能具有重大意義。

近年來，對軌道交通環控系統的節能運行和能耗預測有了較為廣泛的研究[6-7]。牛麗仙等[8]提出了一種基于BP神經網絡的地鐵節假日能耗預測方法，利用反向傳播的神經網絡實現了對地鐵能耗工作日和節假日的分別預測，相比于常規預測提高了地鐵節假日能耗預測的精度。同時，時間序列分析方法作為一種成熟的統計學方法，在諸多領域得到了廣泛應用，如建筑能耗預測[9]、電力預測[10-11]、HVAC故障診斷[12-13]。歐陽前武等[12]利用ARMA模型對廣州市區的商業建筑逐月總能耗進行預測，結果表明ARMA模型在短期建筑能耗預測中可達到較高的精度。周芮錦等[13]對上海某辦公建筑逐月能耗進行預測，采用CensusXl2方法建立ARMA時間序列模型，結果表明模型能夠有效預測辦公建筑能耗。

關于時間序列方法在軌道交通環控系統的能耗預測應用的研究較少。因此，本文提出一種基于ARMA模型的地鐵站環控系統能耗預測方法，通過分析能耗數據的時間序列來預測地鐵站環控系統能耗。

1 ARMA模型原理

ARMA模型即自回歸移動平均模型，是目前最常用的平穩時間序列擬合模型[14]。ARMA模型根據對研究對象長期觀測采集到的時間序列數據，利用參數估計建立數學模型來實現對于該時間序列未來值的預測。以ARMA模型為代表，基于時間序列的預測方法在氣象預報、水文預報和空間科學等領域已得到廣泛的研究和應用[15]。ARMA模型可細分為三類：AR(auto regression，自回歸)模型、MA(moving average，移動平均)模型和ARMA模型。三類模型的區別在于自相關系數和偏自相關系數呈現的性質不同，如表1所示。其中，ARMA(p,q)模型主要由自回歸過程和移動平均過程兩部分組成，其中p為自回歸階數，q為移動平均階數。

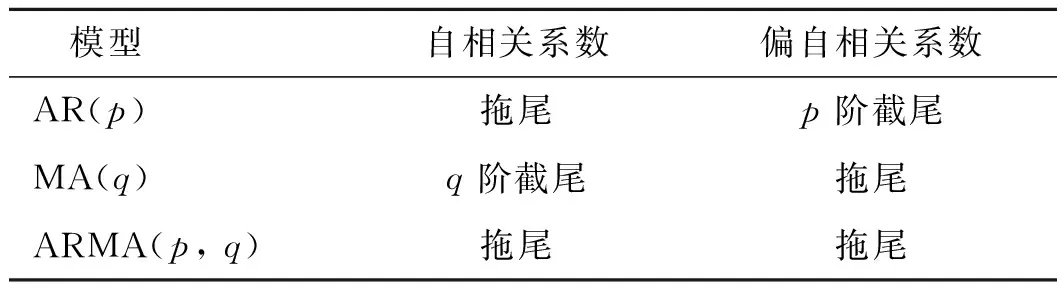
表1 ARMA(p,q)模型的性質Tab.1 Properties of ARMA(p, q)model

ARMA(p,q)模型結構：

Zt=θ0+φ1Zt-1+…+φpZt-p+αt+θ1αt-1+…+θqαt-q

(1)

式中：Z為觀測值，t為時間，Zt為t時刻下的觀測值；{φ}，{θ}為各項系數；αt為殘差序列。引進延遲算子B，式(1)可簡寫為：

φ(B)Zt=θ0+θ(B)αt

(2)

式中：φ(B)和θ(B)分別為AR模型和MA模型的特征多項式。

φ(B)=1-φ1B-φ2B2-…-φpBp

(3)

θ(B)=1-θ1B-θ2B2-…-θqBq

(4)

2 ARMA模型構建

ARMA模型構建流程如圖1所示，分為5個步驟。

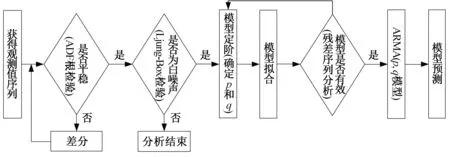
圖1 ARMA模型構建流程Fig.1 Flowchart of ARMA model building

1)平穩性檢驗。時間序列的平穩性代表時間序列的統計性質關于時間平移的不變性。對地鐵站環控系統能耗數據進行平穩性檢驗時，如果數據為非平穩時間序列，需要對序列進行差分運算，直至序列平穩。

2)白噪聲檢驗(純隨機性檢驗)。序列的各項數值之間不相關，序列在進行完全無序的隨機波動，這樣的序列稱為純隨機時間序列(白噪聲序列)。純隨機時間序列是沒有信息可提取的序列，如果序列為白噪聲序列，應當停止分析。

3)模型定階(模型識別)。結合數據樣本時序圖和AIC信息準則，確定模型自回歸系數p和移動平均系數q的最優組合。

4)模型擬合。根據已經確定的最優參數p和q，對平穩非白噪聲時間序列進行擬合，構建ARMA(p,q)模型。

5)模型檢驗。對模型進行顯著性(有效性)檢驗，檢驗模型是否將樣本信息進行充分提取。當模型檢驗為無效模型時，重復步驟3，直至模型有效。

3 仿真實驗與結果分析

3.1 數據描述

本實驗采集北方某城市地鐵站環控系統的實際運行數據進行能耗預測。該城市某一地鐵站環控系統由2臺送風機、2臺排風機、2臺回風機、4臺冷卻泵、4臺冷凍泵、3臺制冷機及一系列閥等組成，子系統結構如圖2所示。實地采集該地鐵站2013-08-21—2013-08-26的6日實際運行數據。通過布置于地鐵站內外的電表和傳感器等監測地鐵環控系統中各設備的運行參數和能耗，計算得出環控系統的總能耗。數據采集時間間隔為5 min，最后得到1 728個數據樣本。

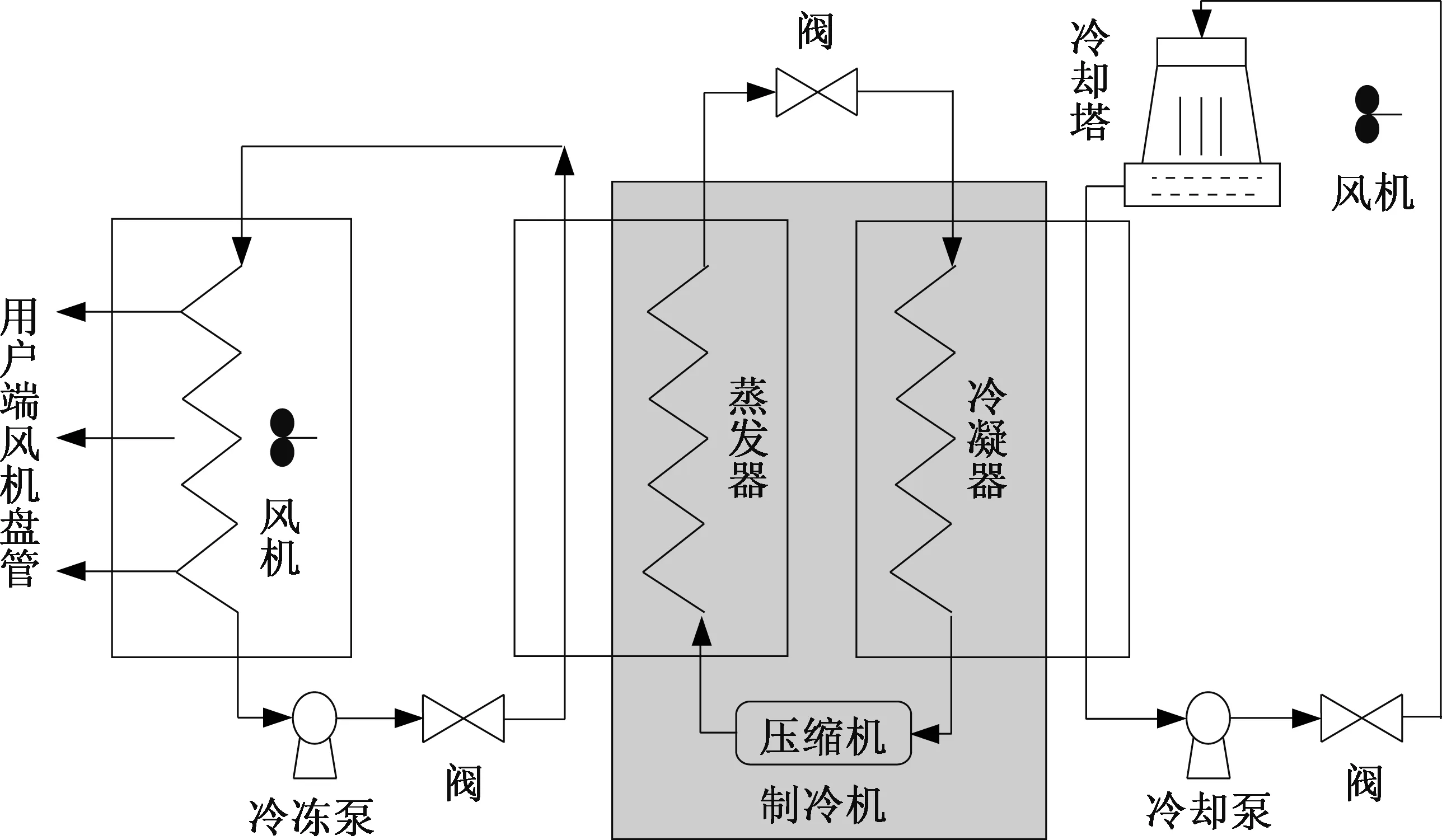
圖2 地鐵站環控系統結構Fig.2 Structure of a metro HVAC system

3.2 仿真實驗

圖3所示為北方該城市某一地鐵站環控系統2013-08-21—2013-08-26的實際能耗數據時間序列。23∶00—06∶00(次日)，由于地鐵停運，環控系統能耗維持在最低水平；白天地鐵運行時能耗明顯增加。由于地鐵站外天氣變化和每日客流量變化等不確定性因素的影響，地鐵站環控系統能耗呈現出一定的不確定性[16]。由圖3可知，原始能耗數據序列整體上并無明顯持續上升或下降趨勢；在平均值23.4附近隨機波動，且波動范圍有界，因此可初步判定能耗數據序列是平穩時間序列。

圖3 地鐵站環控系統能耗時間序列Fig.3 Time series of energy consumption of metro HVAC systems

時間序列的平穩性檢驗包括時間序列檢驗法和單位根檢驗法。為了進一步判斷能耗數據序列是否平穩，本文對能耗數據序列進行ADF根檢驗。ADF假設檢驗：假設能耗數據序列存在單位根，即時間序列不平穩。在3種不同顯著性水平下展開檢驗，1%：嚴格拒絕原假設；5%：拒絕原假設；10%：不能拒絕原假設。能耗數據序列的ADF根檢驗結果如表2所示。由表2可知，檢驗統計量adf=-3.63 < -3.43 < -2.86 < -2.57；且P=0.005 < 1% < 5% < 10%，因此拒絕原假設，可認為能耗數據序列是平穩時間序列。

Ljung-Box統計檢驗是常用的白噪聲檢驗方法[11]。為檢驗能耗數據序列是否為白噪聲序列，對能耗數據序列做延遲4階的Ljung-Box統計檢驗，P均明顯小于顯著性水平0.01，因此原始序列不能判定為白噪聲序列，即原始序列中包含不可忽略的相關信息。

表2 原始序列ADF根檢驗Tab.2 ADF test of original data sequence

注：adf為ADF單位根檢驗的統計量；P為置信度，即接受原假設檢驗的概率。

模型定階是估計自回歸階數p和移動平均階數q的過程。圖4所示為能耗數據序列的自相關圖和偏自相關圖。橫坐標為滯后階數，縱坐標分別為自相關系數和偏自相關系數，陰影區域為系數的置信度邊界。由圖4可知，自相關系數呈衰減趨勢，滯后57階后在95%置信區間內可視為趨近于0，相關系數衰減的過程相對連續且緩慢，因此自相關系數可視為不截尾，確定q=0。觀察偏自相關圖，在滯后1、2、3、4階時，偏自相關系數顯著大于0；滯后5階后，偏自相關系數迅速衰減趨于0，且在95%置信邊界內隨機波動，性質表現為5階截尾，因此可初步確定p=5。

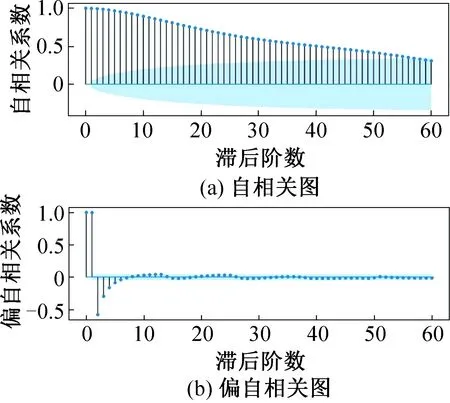
圖4 序列自相關圖和偏自相關圖Fig.4 ACF and PACF charts of data sequence

為進一步確定最合適的自回歸階數，在p=5附近采用AIC信息準則估計不同自回歸階數對模型擬合精度的影響，如表3所示。由表3可知，當p=5時，AIC取得最小值，因此選取p=5。當確定最佳自回歸階數和移動平均階數，可對能耗數據序列進行模型擬合。根據表1，構建ARMA(5, 0)模型，即AR(5)模型。

表3 不同自回歸階數下的AIC信息準則值Tab.3 AIC values of different p order

3.3 模型顯著性檢驗

模型的顯著性檢驗主要檢驗模型的有效性，即擬合模型是否充分提取觀測值序列中所有的樣本相關信息。當擬合模型為有效模型時，殘差序列αt中不存在任何相關信息，從而殘差序列αt為白噪聲序列。采用4種方法對模型顯著性進行檢驗。

1) 相關圖檢驗

圖5所示為能耗預測模型的殘差序列αt的自相關圖和偏自相關圖，陰影區域為系數的置信度邊界。由圖5可知，自相關系數和偏自相關系數在0階之后，在95%置信邊界內以0為均值隨機波動，且數值上均趨近于0，呈現出截尾的性質，因此可認為殘差序列不存在自相關性。

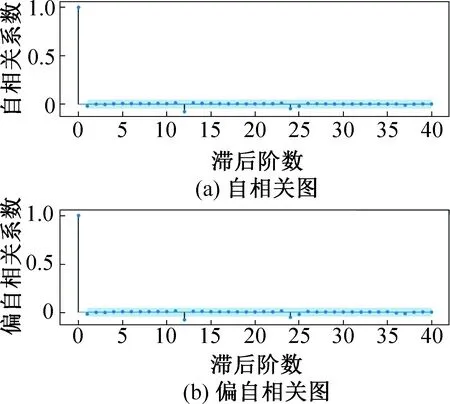
圖5 模型殘差序列的自相關圖和偏自相關圖Fig.5 ACF and PACF of model residual sequence

2) DW檢驗

DW(Durbin-Watson，德賓-沃森)檢驗是檢驗殘差自相關性的常用方法[17]。檢驗統計量DW的取值范圍為區間[0, 4]，當DW趨近于0時，序列顯著正相關；當DW趨近于2時，序列不存在自相關性；當DW趨近于4時，序列顯著負相關。對能耗預測模型的殘差序列αt進行DW檢驗，經計算，檢驗統計量DW=1.31，因此可判定殘差序列不存在自相關性。

3) QQ分布

為判斷能耗預測模型的殘差序列αt是否服從正態分布，將殘差序列繪制QQ分布，如圖6所示。由圖6可知，擬合模型的殘差序列值基本在擬合直線y=0附近呈近似對稱分布，即殘差序列服從均值為0、方差不變的正態分布。因此，可判斷殘差序列為白噪聲序列。

4) Ljung-Box檢驗

Ljung-Box test是基于一系列滯后階數，對時間序列是否存在滯后相關的一種統計檢驗[14]。對能耗預測模型的殘差序列αt做假設檢驗，原假設：序列相關系數等于0，即序列為白噪聲序列。檢驗結果如表5所示。當取顯著性水平為0.01，最后一列檢驗概率顯著大于顯著性水平，說明序列相關系數與0沒有顯著差異，即可認為殘差序列為白噪聲序列。

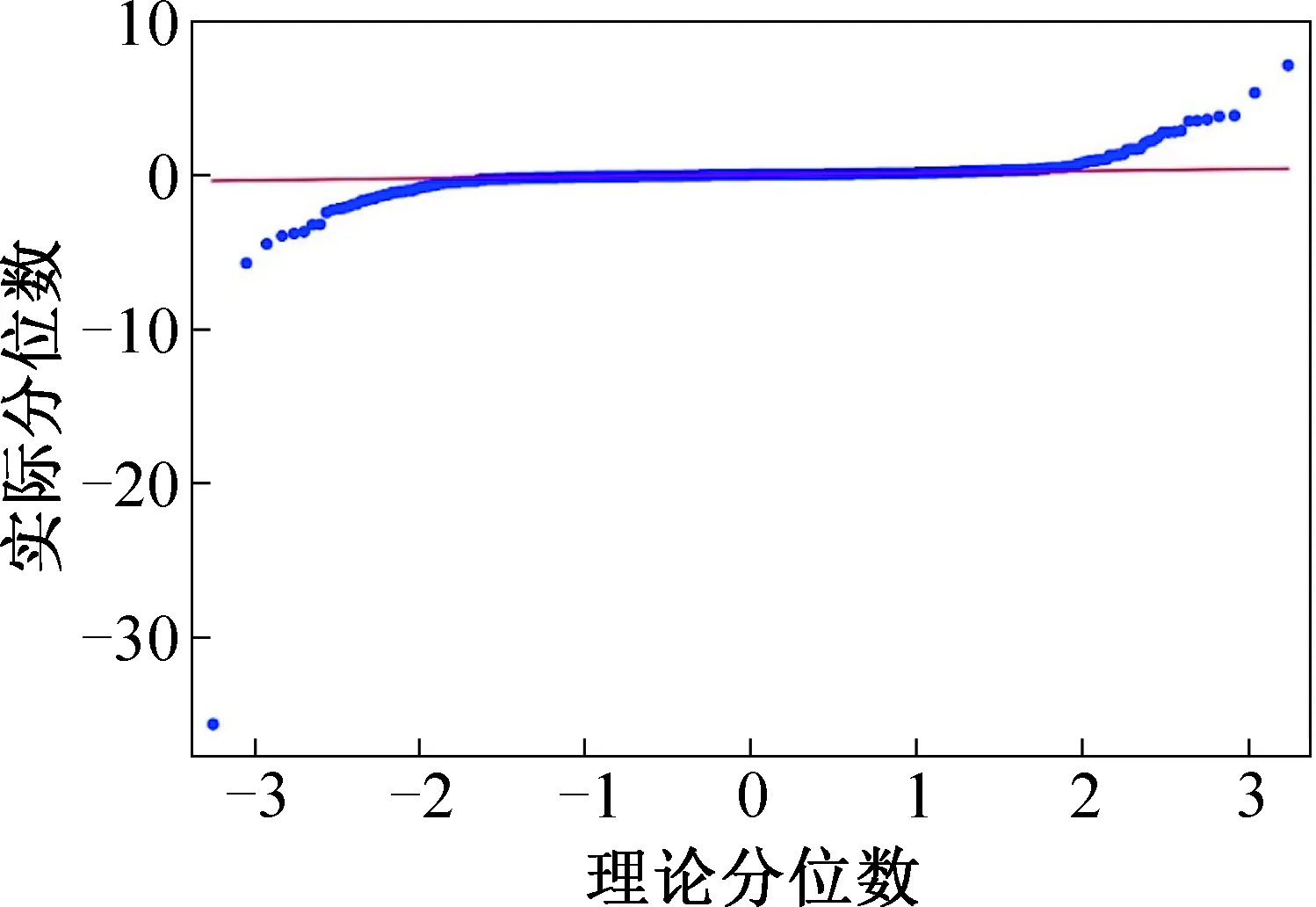
圖6 模型殘差序列QQ分布Fig.6 QQ plot of model residual sequence

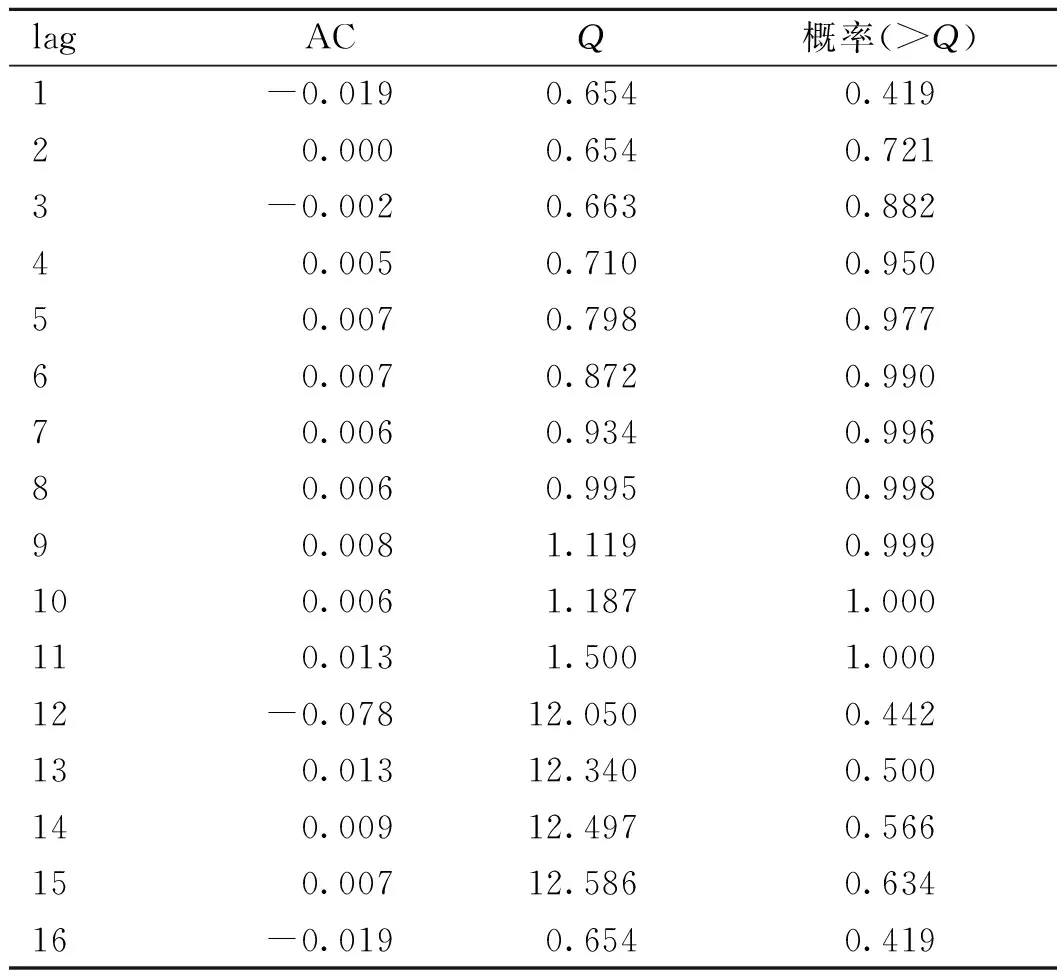
lagACQ概率(>Q)1-0.0190.6540.41920.0000.6540.7213-0.0020.6630.88240.0050.7100.95050.0070.7980.97760.0070.8720.99070.0060.9340.99680.0060.9950.99890.0081.1190.999100.0061.1871.000110.0131.5001.00012-0.07812.0500.442130.01312.3400.500140.00912.4970.566150.00712.5860.63416-0.0190.6540.419

注：lag為滯后階數，AC為自相關系數，Q為Ljung-Box檢驗的統計量。

綜上4種對能耗預測模型的殘差序列αt的檢驗分析，一致判定模型殘差序列中不存在任何相關信息，說明擬合模型為有效模型。

3.4 模型預測分析

模型構建之后，可利用能耗數據對模型進行擬合程度分析。模型觀測值與擬合值的擬合序列如圖7所示。由圖7可知，擬合值與觀測值基本吻合。

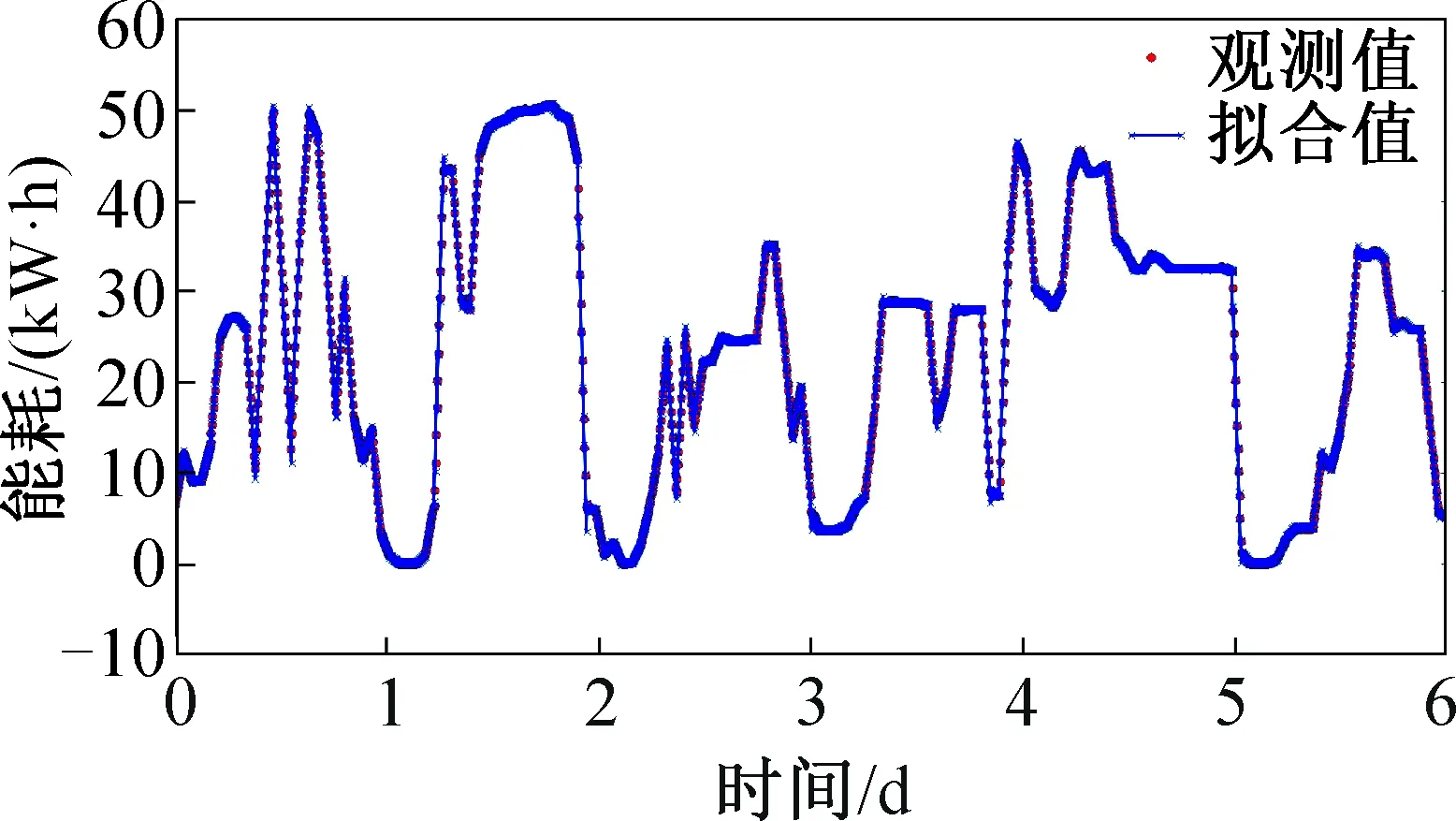
圖7 地鐵站環控系統能耗擬合分析Fig.7 Energy consumption fitting analysis of metro HVAC systems

MAE(平均絕對誤差)和RMSE(均方根誤差)可分別用式(5)、式(6)計算：

(5)

(6)

根據上式，可進一步對擬合模型進行性能評估。經計算，MAE和RMSE分別為0.101和0.470。因此，該模型對地鐵站環控系統能耗數據序列具有很好的擬合效果。

4 結論

地鐵站環控系統的建模和預測對于提高環控系統運行效率和地鐵站節能運行具有重要意義。本文通過對地鐵站環控系統能耗數據進行時間序列分析，提出了一種基于ARMA模型的地鐵站環控系統能耗預測方法，介紹了建模的分析過程和步驟。通過實地采集地鐵站環控系統能耗數據，對能耗數據進行平穩性檢驗和白噪聲檢驗，構建能耗預測ARMA模型，采用4種方法對擬合模型的有效性進行檢驗。得到如下結論：

1)該方法充分考慮了地鐵站環控系統能耗的不確定性因素，建立了有效的ARMA模型，提取出地鐵站環控系統能耗數據中有價值的信息。

2)對于地鐵站環控系統能耗預測具有較高的擬合精度，MAE和RMSE分別達到0.101和0.470，具有較高的理論意義和應用價值。

本文受華中科技大學自主創新研究基金(5003120005)項目資助。(The project was supported by Independent Innovation Research Foundation of Huazhong University of Science and Technology (No.5003120005).)