表征駕駛風格和駕駛員能力的駕駛員模型

王超， 郭孔輝， 許男， 張琳， 劉洋， 鄭磊， 劉濤

(1. 吉林大學 汽車仿真與控制國家重點實驗室，吉林,長春 130025；2. 長春孔輝汽車科技股份有限公司，吉林,長春 130012 3. 中國第一汽車集團公司技術中心，吉林,長春 130011)

在人-車-路閉環系統中，駕駛員兼做道路狀況的感知環節和車輛操作的決策環節，對車輛安全穩定的行駛以及乘坐人員的感受起著重要作用. 駕駛員模型從控制的角度，對真實駕駛員的車輛操作行為進行模擬，被廣泛應用于車輛仿真開發、主動安全控制系統設計[1-2]及智能車控制系統開發[3-4]. 更準確更真實地反應駕駛員的行為，是駕駛員模型開發的目標之一. 其中DYNAware仿真平臺的駕駛員模型以線性單軌車輛模型和半經驗輪胎模型構建控制內模，將駕駛員軌跡跟隨行為轉化為最優控制問題進行求解，軌跡跟隨效果較好，并且通過設定駕駛員操作參數和車輛響應參數的極值定義駕駛員風格，仿真中顯現出了不同的駕駛方式. 模型預測控制(MPC)由于其滾動更新預測區間進行尋優的特點，與真實駕駛員行為習慣相近，被廣泛應用于車輛轉向控制行為的建模[5-6]. 模型預測控制被應用于模擬駕駛員學習、自適應車輛特性并進行轉向操作決策的行為，設定了幾個自由參數以模擬不同的駕駛員，包括視野距離的遠近、側向位移與車身方位角的權重比，并根據22位真實駕駛員的駕駛結果進行了誤差統計與分析，更豐富的描述了駕駛員. 基于隨機模型預測控制建立駕駛員轉向行為模型，應用側向橫擺二自由度車輛模型與UniTire輪胎模型[7]建立預測模型，將駕駛員對輪胎側偏角的估計以正態分布的形式建模，表征熟練駕駛員與生疏駕駛員的估算差別.

盡管上述文獻對駕駛員的駕駛方式進行了一定區分，但真實駕駛員面臨駕駛環境復雜多變，且不同駕駛員對車輛操縱能力也不盡相同. 因此，本文基于最優預瞄理論，通過4個自由參數表征：駕駛員的視野范圍大小、遠近重視程度、決策意愿、決策精度差異. 從而豐富了模型對駕駛員的駕駛風格及駕駛員能力的模擬.

1 駕駛員的視野特征與決策意愿建模

真實駕駛員的駕駛習慣往往是關注視野中前方一段道路. 如果這段道路中存在n個預瞄點，與每一預瞄點處匹配的預瞄時間為tl～tn，跟隨誤差為el～en. 隨著車輛的移動，這些預瞄點的信息也在不斷更新，駕駛員由此進行行駛決策，從而模型具有類似于模型預測控制的滾動更新的特點. 為使每一預瞄點的跟隨誤差值最小，則有

(1)

綜合考慮全段預瞄軌跡的跟隨誤差值最小，建立二次型指標函數，則有

(2)

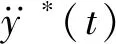
以上為以單一跟隨誤差最小目標的多點預瞄駕駛員模型，而因駕駛員的駕駛風格不同(或行駛條件不同)，為了穩定車身或駕乘感受舒適，在一定程度上放棄跟隨誤差最小指標，以換取較小的側向加速度. 加速度最小指標可以描述為

(3)

綜合式(1)與式(3)，便可將多點預瞄模型發展為多點雙目標決策模型. 在預瞄點i處，分別以權系數p和q，表征駕駛員對跟隨誤差及側向加速度的決策意愿，建立指標函數

(4)

綜合以上指標函數，設每一預瞄點處的權系數為wi，則有

(5)

(6)

由于車速一定的情況下，Ti越大，預瞄距離越遠. 所以，當m>0時，視野遠處軌跡信息權重高；當m<0時，視野近處軌跡信息權重高；當m=0時,wi(Ti)=1,軌跡沒一點的權重相同. 同時，|m|越大，相鄰兩個預瞄點的權重差距的越大，t1～tn預瞄區間內的遠近重視區別越明顯. 通常取值范圍在m∈[0,5]即可表現出駕駛員較豐富的視野特征.

2 駕駛員決策精度差異建模

上文提到的側向加速度決策，是基于最優理論得到. 但真實的駕駛員不會像計算機一樣，在每一次決策時都能夠計算出側向加速度的最優值. 更貼近現實的應是駕駛員每次決策的加速度值都在最優值周圍的一定范圍，并且這一范圍應有一定規律可循. 文獻[6]中，將駕駛員對輪胎真實側偏角的估計考慮為一種高斯函數的分布行為，同樣在這里，假設駕駛員的決策行為符合一定的高斯分布，從這一角度描述不同決策精度的駕駛員.

(7)

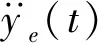
(8)

令：

(9)

由式(8)和式(9)得

(10)

(11)

3 駕駛風格與駕駛員能力

以上的理論建模階段，可以看到表征駕駛員特征的參數在原有預瞄時間tp，神經反應滯后時間td，以及肌肉操作滯后時間th的基礎上，發展為更豐富和貼近真實駕駛員的視野特征、決策取舍特征及決策精度特征的描述方式. 由4個自由參數表示這些特征，如表1和表2所示.

表1 表征駕駛風格及能力的物理量及意義

這里提出了駕駛風格和駕駛員能力兩個相互獨立又可以交叉的概念. 駕駛風格，表現駕駛員對車輛駕駛方式的取向，屬于駕駛員的意愿：一種為對遠近軌跡信息的取舍;另一種為對跟隨精度和乘坐感受的取舍，與駕駛員本身能力無關. 因為駕駛員能力是駕駛員對駕駛方式決策的最優側向加速度的實現能力，成熟駕駛員的決策相對更容易接近最優值，生疏駕駛員決策相對更不易接近最優值. 駕駛風格和駕駛員能力的概念互不影響，可以自由匹配.

4 仿真驗證

在Matlab R2013a/Simulink和Carsim 8.1建立聯合仿真平臺，以雙移線工況進行仿真驗證，主要從預瞄區間大小、視野窗函數選擇、跟隨誤差側向加速雙指標權重值以及駕駛員決策精度系數4個方面進行仿真對比.

針對視野區間的仿真如圖1所示. 車速為80 km/h，視野窗函數為wi=1，即視野區間內所有預瞄點權重相同，預瞄點個數n=10，不考慮側向加速度指標以跟隨誤差最小為單一目標，并忽略決策偏差，分別在視野區間[t1,1,t1,10]=[0,0.6 s]和[t2,1,t2,10]=[0,1.0 s]進行仿真對比. 在圖1中，兩種預瞄方式下，駕駛員轉向操作的起始位置分別為X1=46.69 m，X2=37.82 m. 由于此處所述“預瞄視野”為駕駛員決策的依據，所以預瞄視野越長，就越能夠提前獲取道路信息，并進行操作決策.

圖1 駕駛員視野區間大小對軌跡跟隨的影響Fig.1 Effect of driver's visual field for path tracking

圖2 駕駛員視野窗函數對軌跡跟隨的影響Fig.2 Effect of horizon-window for path tracking

針對駕駛員決策取向的仿真結果如圖3、圖4所示. 其中跟隨誤差權重參數為p，側向加速度權重參數為q，車速設定為60 km/h，視野區間[t1,1,t1,10]=[0.3,0.6] s，視野窗函數為wi=1，最大跟隨誤差和最大側向加速度如表2所示.

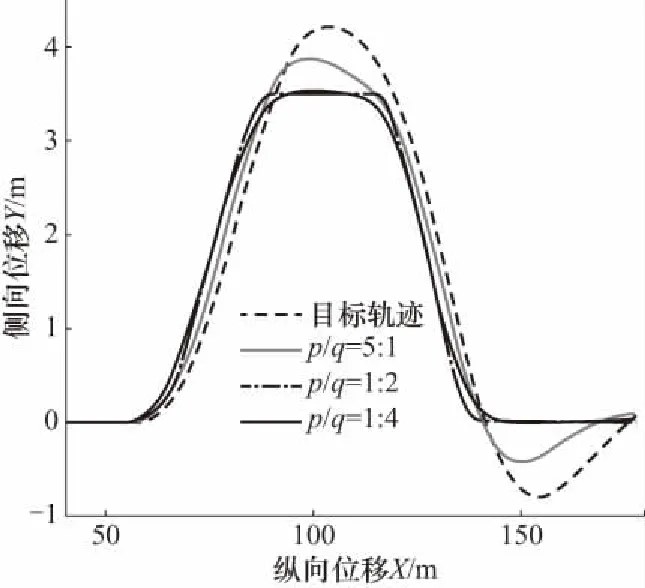
圖3 駕駛員決策取向對軌跡跟隨的影響Fig.3 Effect of decision intention for path tracking

圖4 駕駛員決策取向對側向加速度的影響Fig.4 Effect of decision intention for lateral acceleration

表2 決策取向參數對跟隨誤差和側向加速度的影響

可以看到，決策取向參數p/q對跟隨誤差和側向加速度大小的影響明顯，與理論相符.p/q的值越大，說明駕駛員模型所模擬的駕駛員對跟隨精度要求的越高，偏向于駕駛的精準性；p/q的值越小，說明所模擬的駕駛員希望側向加速度最大值越小，偏向于駕駛的舒適性.

圖5 決策能力對軌跡跟隨的影響Fig.5 Effect of driver's decision ability for path tracking

5 結 論

以駕駛員決策行為及側向物理模型為基礎，建立以側向加速度與方向盤轉角的穩態增益Gay為經驗的，以駕駛員視野為單位的滾動尋優車輛轉向操作算法，內部自由參數能夠表征駕駛風格及駕駛員能力.

區分了駕駛風格和駕駛員能力的概念. 以視野特征，決策意愿特征表征駕駛風格，代表駕駛員的決策意愿；以決策精度特征表征駕駛員能力，代表駕駛員對最優決策的實現能力. 兩個概念彼此獨立，可相互匹配.

視野特征以參數[t1,tn]表征駕駛員的視野范圍大小，以視野窗函數wi=tim表征遠近重視取向；決策意愿特征以權值比p/q表征駕駛員對跟隨誤差和側向加速度的取向；決策精度差異特征以方差參數σ表征真實決策值與最優決策值的差距程度. 4組自由參數的相互匹配，拓寬了駕駛員模型的模擬范圍.