全波形激光測距幅相誤差改正方法

劉榮榮 毛慶洲

摘要：針對全波形激光測距中存在的幅相誤差問題，提出一種基于神經網絡的幅相誤差改正方法。利用非合作目標探測信息，通過提取回波波形的形狀信息、能量信息、梯度信息、對稱性信息及距離信息特征參數，根據皮爾遜相關系數對特征參數進行分級，建立多回波特征信息與幅相誤差改正的神經網絡模型以校正全波形激光測量中各通道幅相誤差的影響。實驗使用5%、20%、60%、80%標準反射板及激光采集模塊在室內對7種距離進行數據分組采集和處理，并與傳統測量方法進行對比。結果表明，該方法可以有效減小全波形激光測量中幅相誤差的影響，測量精度提高了51.2%以上。

關鍵詞：全波形激光雷達;幅相誤差;神經網絡;回波特征提取;信號檢測

中圖分類號：P207 文獻標志碼：A

引言

全波形激光測距是一種典型的非合作目標距離測量與反射強度獲取方法，在國土測繪、軍事偵察及工業測量等領域中發揮著重要的作用，其測量精度及效率在激光測量中廣受關注。幅相誤差是高精度激光測量中的重要誤差來源，主要是由各通道回波幅值不同引發的檢測相位變化引起。

針對幅相誤差這一問題，Palmese等提出在有源校正前提下的幅相誤差解決方法;Friedlander提出了一種陣列幅相誤差迭代算法來避免計算校正源;王鼎等構造二次代價函數，通過反復迭代求解估計幅相誤差;鄭煜等利用雷達的雜波特性提出一種基于雜波子空間特征的雷達幅相誤差自校正方法以解決幅相誤差較大的問題，但是算法的適用范圍有限;楊璋等針對均勻線陣和圓陣給出了幅相誤差自校正方法，但迭代算法計算量較大，計算效率有待提高。本文提出一種基于神經網絡的全波形激光測距幅相誤差改正方法，通過建立波形特征信息與幅相誤差的改正模型準確計算幅相誤差的改正量，以降低幅相誤差的影響，提高測量精度。

1全波形激光雷達測量原理

1.1測量原理

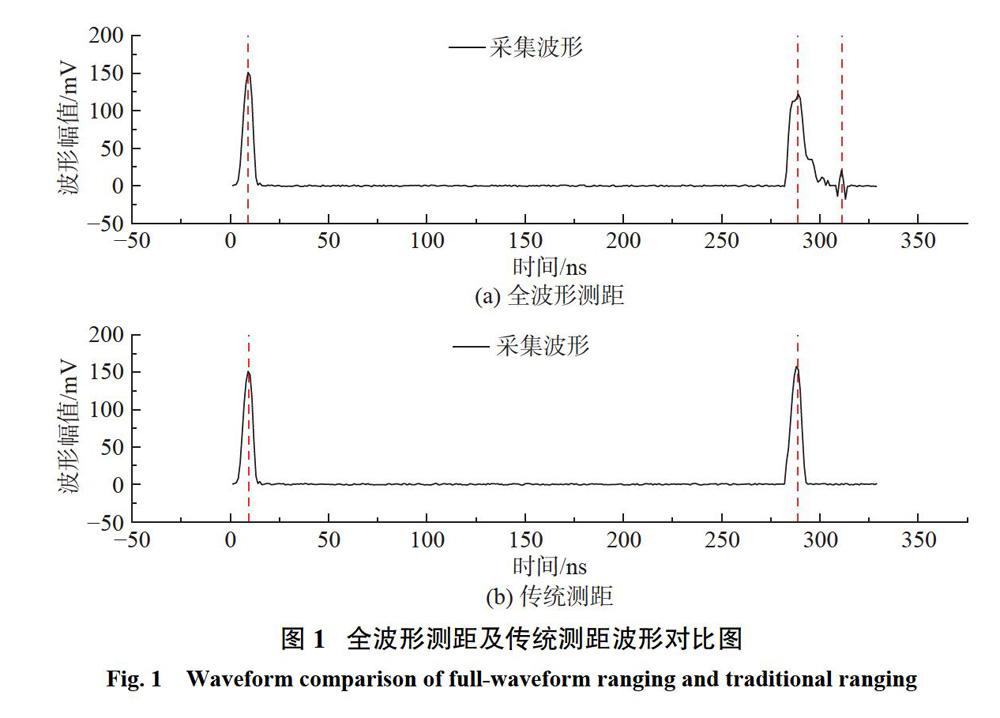
全波形激光雷達發射單次激光脈沖后，對發射脈沖及激光腳點內探測目標的后向散射回波進行全數字化記錄和存儲，不僅能夠實現高精度測距，還能提供豐富的地物垂直結構信息，如圖1所示。通過分析其脈沖相位、幅度、脈寬及脈沖個數等全波形回波特征信息，可以挖掘更深層次的地物屬性信息。

與傳統激光雷達測量相同，激光發射器向探測目標發射激光信號，再由信號接收器接收來自探測目標的后向散射信號，通過記錄激光器發射種子光時刻to與回波接收時刻t1，即可計算激光發射位置與探測目標之間的距離D，D的表達式為

為精確計算回波信號至種子光信號的時間差，目前已有的方法包括峰值法、加權法、重心算法及高斯擬合中心法等。由于全波形回波信號并非典型高斯回波，直接使用上述方法計算飛行時間存在偏差，使測量精度降低。本文結合多種波形中心計算方法與波形特征信息，建立神經網絡模型以準確計算脈沖飛行時間。

1.2幅相誤差

在全波形激光雷達信號處理中，由于激光雷達測量環境及目標的多樣性及復雜性，不同地物測得的反射信號具有各自的特殊性，這些回波的波形特征包含了除測量距離外的大量地物屬性信息及測量環境信息等。全波形信號經過波形分解、峰值檢測等算法可得到收發信號的時刻坐標，初步計算測量距離D。

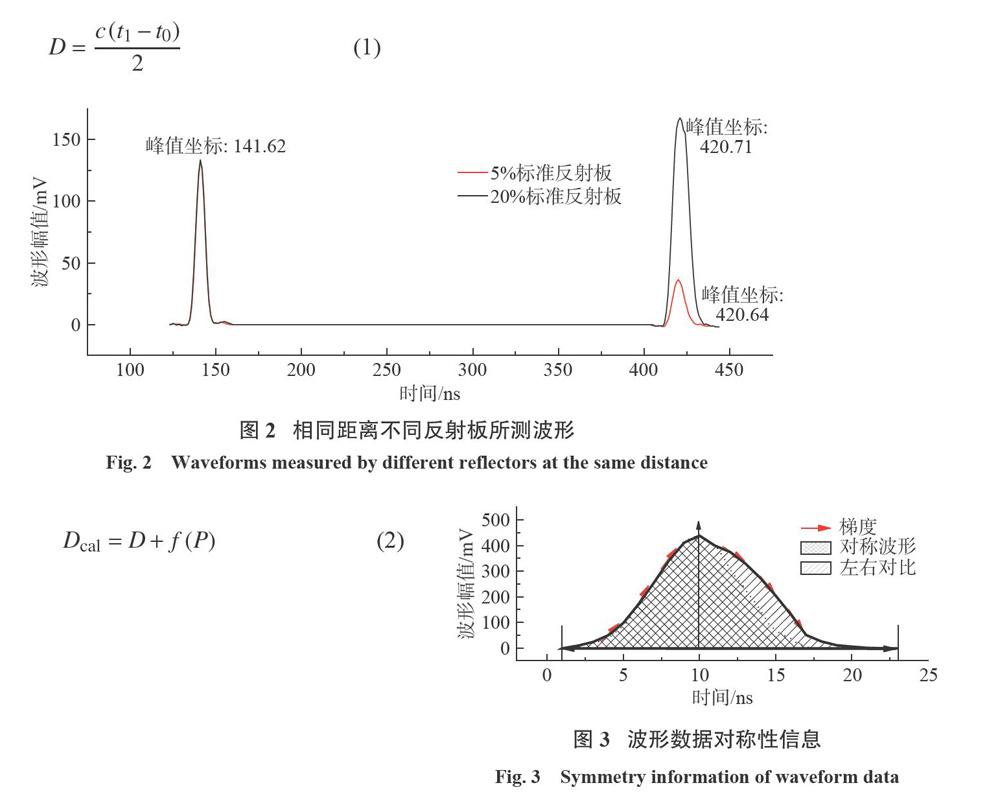
不同通道探測到的回波幅值及相位不同使檢測到的回波峰值位置發生變化，極端情況下由幅相誤差帶來的測量誤差可達厘米級以上。在室內相同距離分別使用5%標準反射板、20%標準反射板及激光數據采集模塊采集種子光及回波波形數據，5%標準發射板對應波形及20%標準反射板對應波形的種子光對齊后，兩組回波幅值及相位均有差異，峰值檢測位置發生“前后漂移”，如圖2所示。

1.3波形特征

幅相誤差使得實測中不同距離回波信號的形態特征發生不同程度的變化，直接由式（1）所得的測距信息D受幅相誤差的影響。為消除幅相誤差的影響，可根據回波波形的形態特征信息P、測距信息D與幅相誤差建立網絡模型廠（P），求解幅相誤差改正數，以計算改正后的測距值Dcal：

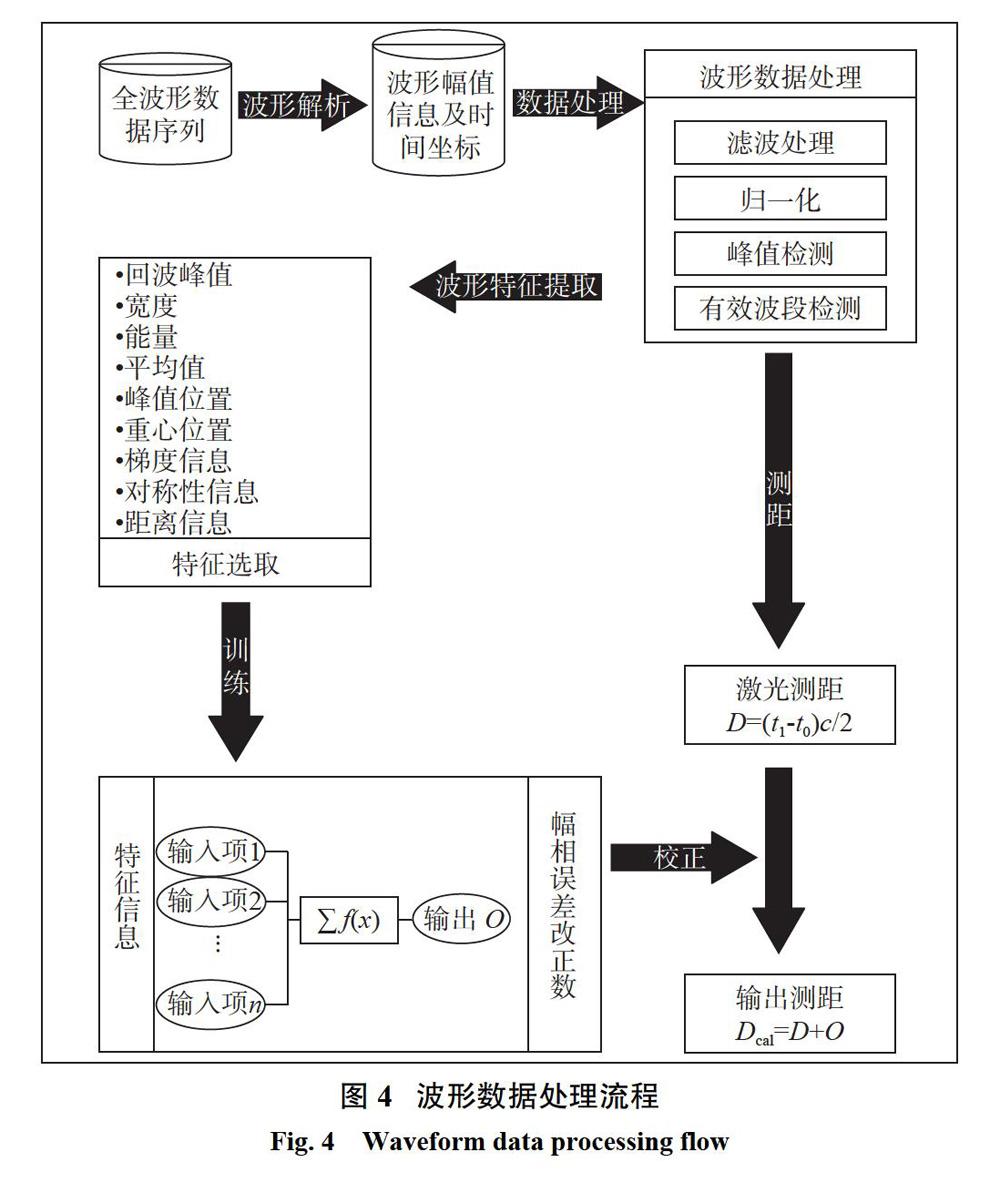
波形信號的特征信息主要包括形狀信息、能量信息及對稱性信息等。全波形信號并非嚴格意義上的高斯型波形，其左右往往呈“此緩彼陡”的非對稱形態。為表征這種非對稱性信息，一是使用上升沿及下降沿的梯度信息，二是使用回波峰值左右半部向量差值表示，如圖3所示。

為表征探測波形在不同通道的形態變化，共選取9類波形特征：回波峰值、寬度、能量、平均值、峰值位置、重心位置、上升沿及下降沿梯度信息、回波對稱性信息及距離信息。假定波形處理后獲取的有效波段為E（e1，e2，…，en），ei為i（i=1，2，...n）時刻采集的波形幅值，則：

1）回波峰值：使用波形幅值最大值及其左右多個波形幅值點，計算加權后回波峰值;

2）回波寬度：根據有效波段檢測閾值，計算回波有效范圍;

3）回波能量：計算有效波段內波形面積;

4）平均值：計算有效波段內幅值的平均值;

5）峰值位置：計算回波峰值對應的時間坐標;

6）種子光與回波中心距離信息：使用高斯函數擬合種子光波形及回波波形，計算波形中心位置坐標時間差;

7）回波對稱性信息：使用三次樣條插值使左右半部的回波向量維度相同，通過計算左右向量差值向量的范數來表征對稱性信息，符號信息由峰值左右波形面積比值賦予，當左面積與右面積比EI/Er≥1時，符號sig=1，反之sig=1;

8）回波重心位置：單一使用高斯擬合在波形采集點較少時會發生“左右漂移”，因此使用迭代法計算回波波形面積二分之一處的時刻坐標來表征回波重心位置;

9）上升沿及下降沿梯度信息：使用4階切比雪夫多項式擬合回波曲線，將上升沿（起始點至峰值點）平均分為4個區間，選擇中間3個位置計算擬合曲線上的1階梯度信息，同理可計算得到下降沿梯度信息。

2波形數據處理方法

2.1波形處理

用激光測距儀采集原始波形數據（由十六進制的特定數據結構組成），對這些數據解析后得到波形幅值及時間坐標信息;再對波形信息進行濾波處理以消除噪聲，同時采用二階導數方法檢測波形的有效信息段，以及對有效波段進行數據歸一化（以便后續結果對比）;最后經提取波形特征及分類后，交由后向傳播（BP）神經網絡處理并對測距結果進行改正。處理流程如圖4所示。

2.2相關性分析

經過波形處理后，從有效波段中提取的波形特征共9類。為減少數據冗余量，提高數據處理效率，需要從9類信息中提取最典型的特征信息。皮爾遜相關系數適用于分布不明、非等間距測度的連續變量情況，其定義為兩個變量之間的協方差和標準差的商。假定向量X，y，則其皮爾遜相關系數p計算公式為

實際測量中使用5%、20%、60%、80%標準反射板在不同距離處進行測量，可以看出不同波形特征信息在不同反射率下的變化有所差異。極強相關的波形特征在4種標準反射板下出現較為明顯的4層分段現象;中等程度相關的波形特征也會出現不同程度（3層及以下）的分層現象;極弱相關的波形特征在不同反射率下變化很小，基本呈現一條線，如圖5所示。因此，在后續進行神經網絡訓練時，輸入項的選擇有：1）選擇3類極強相關特征;2）選擇3類極強相關特征和2類中等強度相關特征;3）選擇所有的9類特征。

2.3神經網絡

BP神經網絡是一種按照誤差逆向傳播算法訓練的多層前饋神經網絡，其特點就是信號的前向傳播與誤差的反向處理，根據層輸入項計算層輸出，再根據計算值與真實值之間的誤差調節參數，直至訓練誤差滿足條件。神經元模型可以簡化為Oj=f（netj））=f（wj^Tx），其中：W為輸入項的權重向量;Xl，X2，X3，…，Xn為神經網絡輸入項，即各類波形特征信息;D為神經網絡輸出項，即幅相誤差改正數。

根據在不同反射板下各波形特征變化大小，設置3種輸入量：1）使用極強相關的3類特征，即總能量、峰值及平均幅值;2）在1）基礎上增加中等程度相關特征，即對稱性信息以及距離;3）使用全部9類波形特征信息。使用80%的實測數據為訓練數據，20%的實測數據為測試數據，檢驗神經網絡模型的可用性及準確度。

3實驗與分析

3.1實驗數據采集

實驗在室內基線場進行，實驗場布置如圖6所示。使用全波形激光數據采集模塊、標準板固定支架及4塊標準反射板（5%、20%、60%、80%）采集波形數據，采樣頻率為1.2 GHz（1 clock=0.8333 ns，為相鄰采樣點的時間間隔），共4個通道，相鄰通道間放大倍數為16倍，由十六進制數據格式存儲原始波形，波形解析后可得到波形幅值及時間坐標信息，經過波形處理后參與BP神經網絡訓練學習。

真實距離數據使用徠卡全站儀TS1115獲取，使用支架固定4塊反射板，選擇7處采集波形數據，共28組數據，每組數據包含1 000對種子光及回波波形數據，共28 000條數據。BP神經網絡使用采集數據中的80%作為訓練數據，20%作為測試數據。圖7所示為相同距離處不同反射板所測得的種子光及回波波形數據，5%及20%標準反射板所測數據由4通道獲取，60%及80%標準反射板所測數據由3通道獲取。

3.2實驗結果

根據2.3節，對9類波形特征重要性大小進行分級，建立波形特征與幅相誤差改正的4層BP網絡模型;依據3類神經網絡輸入項分別輸入波形特征信息，根據網絡輸出對測距進行校正，并與傳統直接計算激光測距的重心法進行對比，比較處理前后脈沖飛行時間的分布。每組測試數據800條，0～200，201～400，401～600，60 1～800對應的飛行時間分別為使用80%、60%、20%、5%標準反射板所測數據，如圖8所示。

3.3結果分析

波形幅相誤差改正精度使用兩類評價參數：一為改正前后激光飛行時間分布的標準差，二為改正前后使用不同反射板在相同距離處1 000次測量的平均值與真實距離之間的最大誤差。表2、3表明使用文中方法減小了測距點分布的離散程度，使用不同反射板測得的最大誤差可減少51%以上。使用5類特征參與模型訓練即可得到較好的結果，說明使用該方法處理幅相誤差是可行的。

4結論

幅相誤差是高精度激光測量中必須考慮的誤差來源，為減少幅相誤差對激光測量精度的影響，本文提出了一種基于神經網絡的幅相誤差改正方法。通過提取波形的多項特征信息建立幅相誤差改正的神經網絡模型;使用皮爾遜相關系數表征各波形特征在不同反射率下的變化大小，將波形特征分成3類分別輸入網絡模型進行訓練;以80%的實測數據輸入到BP神經網絡進行訓練，使用剩余20%實測數據進行測試。實驗結果表明，該方法可以有效減小幅相誤差的影響，多次重復測量可以減小測量數據的離散程度，提高測量精度。實驗存在的問題有：只使用4塊標準反射板并在室內進行，缺少對長距離、多反射率情況中幅相誤差的分析;缺少對種子光特征的分析，未來可以從深度學習的角度出發，挖掘種子光及回波數據更深層的特征信息以減少幅相誤差對測量精度的影響。