基于二分法的自動駕駛儀參數優化設計

謝金龍 吳 璋 文世珍 胡 洲

（四川航天系統工程研究所，成都 610100）

導彈的自動駕駛儀即導彈的姿態控制系統，根據制導系統給出的指令信號控制導彈的姿態運動，保證其在飛行中具有足夠的機動性和穩定性，從而確保導彈飛行的安全。自動駕駛儀的主要作用包括保證彈體的穩定性、優化彈體的阻尼特性、提高彈體的機動性能，以及提高彈體的抗干擾能力。

自動駕駛儀的設計方法主要分為經典控制和現代控制。經典的設計方法以經典控制理論為基礎，將系統簡化為單輸入單輸出結構。在簡化模型的基礎上，利用傳遞函數描述系統特性，結合時域響應法、頻域響應法等方法保證系統具有良好的穩定性和快速性。現代控制理論成果主要包含動態逆、滑模變結構、神經網絡、狀態Ricatti方程等。

Nesline等人在1979年提出了一種最優/經典綜合設計法，他的主要想法是通過對系統傳遞函數的頻率特性提供約束，限制目標函數中增益系數的取值范圍，從而達到最優的控制效果。Mracek等人則系統地提出了應用最優控制理論設計自動駕駛儀的方法原理。

經典控制理論設計的自動駕駛儀能夠直觀地了解所選特征點的時域及頻域特性，因此它在工程實踐中是戰術導彈自動駕駛儀設計的主要方法。但是這種方法需要花費大量的時間和精力調試，設計過程繁瑣，所以找到一種快速的參數設計方法很有必要。

自動駕駛儀設計過程中涉及許多新興的方法，如保護映射、極點配置等。當系統傳遞函數階次較低時，極點配置可以較好地實現頻域設計。當系統傳遞函數階次大于二階時，往往需要用到一些經驗公式，但是這些經驗公式反解得到的增益往往不能很好地穩定系統。

當系統模型比較復雜時，將傳遞函數的某項頻域指標（如幅值裕度）作為性能指標函數再得到性能指標函數關于增益參數的變化曲線，通過選取合適的增益邊界范圍，就可以應用二分法逼近得到相應的參數。對得到的參數進行優化，就可以得到滿足其他約束條件的最優解。二分法可以實現計算機代替人為調參，有效提高了設計人員的工作效率。

1 二分法

定理1（介值定理）設f (x)在[a,b]上連續，且f(a) f (b)＜0，則至少存在一個點ξ∈(a,b)使得f (ξ)=0，即ξ是f (x)=0的根。

為了便于分析，設f (x)在[a,b]上是單調的，則f(x)=0在[a,b]內只有一個實根ξ。

1.1 基本思想

二分法是一種通用的數值近似計算方法，它的基本思想是判斷區間中間值的函數值f ((a+b)/2)的正負號，逐步對半縮小有根區間，直到區間縮小到允許誤差范圍之內，然后取區間的中點為ξ的近似值。

1.2 具體方法

不妨設f (a)＜0, f (b)＞0；記a1=a，b1=b，區間[a,b]的中點 ξ1=(a+b)/2，再計算函數值 f (ξ1)。如果 f (ξ1)=0，則表示待求的根為 ξ1，否則判斷 f (ξ1) f (a)＜0 還是f (ξ1) f (b)＜0。

若 f (ξ1) f (a)＜0，則記 a2=a，b2=ξ1，則求根區間變為 [a,ξ1]；若 f (ξ1) f (b)＜0，則記 a2=ξ1，b2=b，則求根區間變為[ξ1,b]。這樣區間[a2,b2]是方程新的有根區間，它被包含在原有根區間[a,b]之內，且長度僅為原區間的一半。對縮小后的區間[a2,b2]，再計算其中點ξ2=(a+b)/2，判斷f (ξ2) f (a2)＜0還是f(ξ2) f (b2)＜0。

如此重復上述計算過程，經過k次這樣的二分以后，求得的有根ξk區間[ak,bk]的中點ξk=(ak+bk)/2。區間大小。顯然，如果無限二分下去，則

因而定義精度ε，當k足夠大時，|ξξk-ak|≤（bk-ak）/2=（b-a）/2k〈ε，則ξk就是方程f (x)=0的一個滿足給定精度的近似根。

2 自動駕駛儀設計

阻尼-姿態角控制方法是經典控制理論中經常采用的一種方法。常見的俯仰通道阻尼-姿態角方案控制框圖如圖1所示。

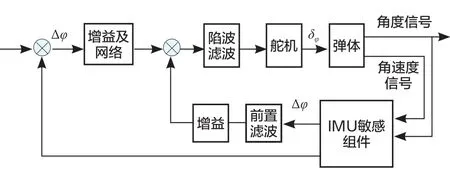
圖1 俯仰通道方案控制框圖

2.1 傳統自動駕駛儀設計

經典控制理論設計的自動駕駛儀是將系統簡化為單輸入單輸出結構，用傳遞函數描述系統特性，通過根軌跡法、時域分析法、頻域分析法來設計系統。這種方法能夠直觀地了解所選特征點的時域及頻域特性，因此在工程實踐中，它是戰術導彈自動駕駛儀設計的主要方法。但是這種方法需要花費大量的時間和精力調試，設計過程繁瑣，尤其當氣動模型發生變化時，自動駕駛儀需要重新設計，所以找到一種快速的參數設計方法很有必要。

2.2 變結構控制方法

變結構控制是一種新興的控制系統設計方法，其非線性表現為控制的不連續性。從理論上說，由于滑動模態可以按需要設計，滑模控制系統的魯棒性能比一般系統好。然而滑模控制中切換函數在不同滑動模態的切換會引起系統的抖振現象，為了克服滑模控制的抖振問題，國內外學者進行了許多不同的探討，其中比較有代表性的是準滑動模態法、趨近律法及濾波法等。

2.2.1 基于變結構控制系統設計

以滾轉通道為例，設滾轉通道的狀態方程為：

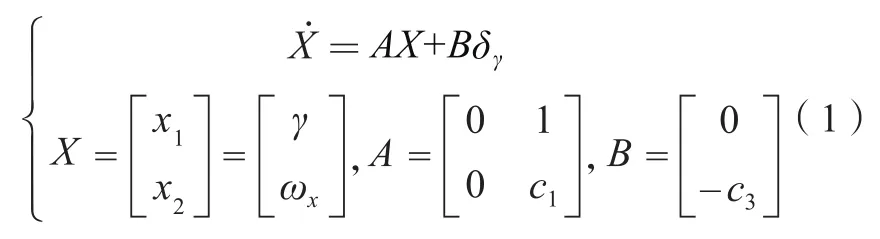
滾轉通道姿態控制的目的是使滾轉角趨向穩定，因此定義誤差變量e = γ，定義滑動模態s為：

對s微分，得到：

定義趨近律為：

則控制律為：

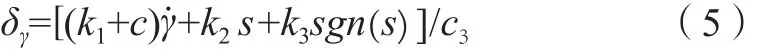
2.2.2 頻域特性分析

將變結構控制的非線性特性進行簡化，可實現線性控制。以滾轉通道為例，令k3＝0則控制律可以簡化為:

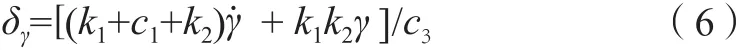
因此，變結構控制在這種特定的情況下等效為1個PD控制器。

選取k1＝10，k2＝10得到10s時刻頻域響應情況，如圖2所示。

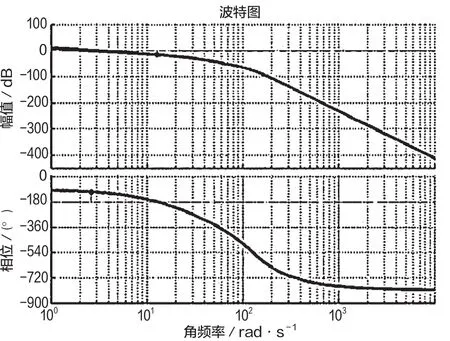
圖2 10s時刻頻域響應情況

2.2.3 總結分析

k1、k2經過多次調試，滾動通道的幅值裕度在16.1dB左右，相位裕度在75.5°左右。變結構控制存在的不足為：（1）滾動通道的響應效果與k1、k2的選取有很大關系，當k1、k2較小時，滾動通道的幅值裕度較大，響應時間較慢；（2）對系統模型的要求較高，當模型階次大于二階時，需要采用降階方法，會對模型的精確性產生影響。

2.3 基于二分法自動駕駛儀設計

與變結構控制方法相同，基于二分法的自動駕駛儀同樣設置成一個PD控制器。以阻尼回路為例，阻尼回路的開環傳遞函數與阻尼回路參數相關，通過這個傳遞函數可以得到阻尼回路的幅值裕度、相位裕度、調節時間等頻域及時域指標。

2.3.1 二分法逼近參數

將頻域指標中的幅值裕度作為性能指標函數F，那么F就能寫成與阻尼回路參數K 相關的函數:F=f(K)。經典控制理論設計中，對幅值裕度和相位裕度都有相應的指標要求,如要求幅值裕度不小于16dB。通過二分法可以迅速找到相應的增益Km，使得特征點的幅值裕度為16dB。

二分法要求目標函數呈現單調變化。對于靜穩定系統，當增益K ＞0時，系統穩定。隨著增益K的增大，系統的幅值裕度減小，因此幅值裕度函數f (K)是一個單調遞減函數。但是當增益K繼續增大時，系統有可能出現振蕩及失穩現象，因此，應用二分法時需要選擇合適的邊界范圍。

選取10s特征點進行頻域設計，找到幅值裕度分別為3dB和50dB的增益K2、K3。將[K2,K3]作為邊界范圍，采用二分法逼近得到幅值裕度為16dB的增益Km。

2.3.2 參數優化

二分法逼近得到的增益Km滿足了控制系統對幅值裕度的要求，但是相位裕度、截止頻率、超調量、調節時間等指標未必能滿足要求。因為幅值裕度函數是單調遞減函數，增益K在(0,Km]范圍內都能滿足幅值裕度要求。

取精度D=100，將增益Km分成100份，Ki= i/100×Km，i =1，2，…，100。

分別計算相應增益的相位裕度、超調量、調節時間等，剔除相位裕度及超調量不滿足要求的情況，選出其中調節時間最優的增益。

10s時刻頻域響應情況如圖3所示。

2.3.3 數學仿真分析

為了驗證基于二分法的自動駕駛儀設計的有效性，將設計的參數代入數學仿真進行驗證，滾動通道初始加入姿態角和姿態角速度偏差，全程加入風干擾及結構干擾，仿真結果如圖4所示。

圖3 10s時刻頻域響應情況

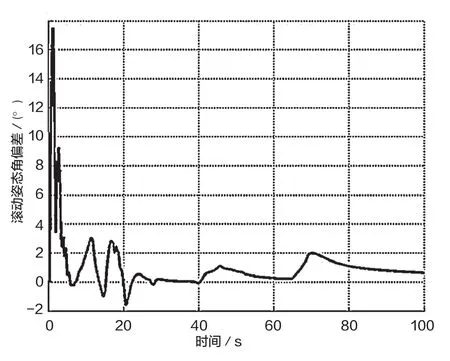
圖4 滾動姿態角偏差

分析圖4可以看出，滾動通道在5s左右將初始姿態角偏差控制到零附近，由于干擾的存在，滾動姿態角在后續也存在一定程度的變化，這說明設計的自動駕駛儀具有較好的魯棒性。

2.3.4 總結分析

通過二分法逼近得到增益Km，使得滾動通道的幅值裕度為16dB，對得到的參數進行優化，得到的幅值裕度在16dB左右，相位裕度在70.1°左右。最終的幅值裕度與二分法逼近得到的幅值裕度基本相同，這是因為二分法逼近得到的增益滿足相位裕度、截止頻率、超調量等指標要求，調節時間是最快的。

通過數學仿真分析結果可以看出，二分法逼近設計得到的自動駕駛儀能夠讓控制系統穩定，具有良好的魯棒性。其優點在于：（1）可以根據不同的頻域、時域需求，設計不同的增益，使人為調參轉換為計算機運算，極大地降低了系統設計的工作量；（2）當系統模型階次較高時，二分法不會受到影響。

3 結束語

傳統的自動駕駛儀控制系統設計需要花費大量的時間和精力，本文提出的基于二分法的自動駕駛儀參數優化設計方法，將人為調參轉換為計算機運算，極大地提高了系統設計的工作效率。針對二分法的參數進行優化，能夠保證控制系統相應的頻域和時域指標滿足約束要求。數學仿真結果證明了設計得到的自動駕駛儀的有效性。