縊蟶表型性狀對體質量和軟體部重的影響效應分析

叢玉婷，王麗，盧亞楠，魏杰，王媛

（大連海洋大學水產與生命學院，遼寧 大連 116023）

在我國水產動物選擇育種上，人們經常選擇遺傳參數作為育種值，制定出選擇指數、比較選擇方法和進行育種規劃，這項工作很有意義也是比較基礎的工作。貝類種苗繁殖與遺傳育種的重要指標是其殼尺寸和重量性狀，這也是貝類重要的經濟性狀。劉小林[1-2]等分別對櫛孔扇貝和凡納賓對蝦的體質量與多個體形性狀進行了多元分析，得出影響櫛孔扇貝和凡納賓對蝦的體質量的主要體形性狀以及間接和直接作用的大小，建立了估計體質量的多元回歸方程。高寶全[3]等分析三疣梭子蟹形態性狀對體質量的影響。此外，相關的報道還有很多[4-8]。該文選用縊蟶對其體形性狀與體質量和軟體部重之間的關系進行通徑分析和相關分析，建立了體質量和軟體部重的多元回歸方程，研究結果為今后縊蟶的選擇育種工作提供了一定的理論依據。

1 材料與方法

1.1 實驗材料及數據采集

試驗用縊蟶采自莊河貝類養殖場，隨機取樣100只活體帶回實驗室，進行數據采集。首先將100個縊蟶逐一編號，使用游標卡尺分別測量所有縊蟶的殼長（X1）、殼寬（X2）、殼高（X3）共 3 項表型形態參數（圖1）。用電子分析天平稱量縊蟶的活體質量（Y1），去掉貝殼后剝離出軟體部重（Y2）并測量（外部形態測量精確到0.01 mm，重量精確到0.0001 g）。

1.2 數據分析

數據分析采用SPSS 17.0和Excel軟件。對采集的數據進行整理，獲得各性狀的統計參數，進行相關分析和回歸分析，回歸分析是用SPSS軟件中的逐步回歸法（stepwise）進行的，逐步回歸法是對多個變量進行分析的有效方法，建立了以表型性狀估計重量性狀的多元回歸方程，然后進行通徑分析和決定程度分析。分別按以下各式計算相關系數（rxy）、通徑系數（Pi）、相關指數（R2）和決定系數（d）。相關系數（rxy）的計算公式為：

通徑系數（Pi）的計算公式為：

式中：bxi為自變量的偏回歸系數，σxi為自變量的標準差，σy為因變量的標差。相關指數R2=ΣPirxiy，式中，rxiy為自變量與因變量之間的相關系數。

單一自變量對因變量的決定系數di=Pi2，式中，Pi為該自變量對因變量的通徑系數，兩個自變量對因變量的共同決定系數dij=2rijPiPj，式中，rij為兩個自變量之間的相關系數，Pi和Pj分別為這兩個自變量對因變量的通徑系數。

2 結果與分析

2.1 各性狀的描述統計量

縊蟶表型性狀與體質量和軟體部重的統計數值見表1。從表1中可以看出，體質量和軟體質量的變異系數（CV）較大，體形性狀的較小，實驗結果表明在遺傳育種中重量性狀比表型性狀更具有選擇潛力。

表1 縊蟶各性狀的描述統計量（n=100）

2.2 各表型性狀與縊蟶體質量、軟體部重之間的相關分析

對表型性狀、體質量和軟體部重分別進行相關分析（表2），數據分析顯示出各性狀之間的相關系數均達到極具統計學意義水平（P＜0.01），這也進一步說明了該試驗所選的這幾項指標進行相關分析是有意義的。其中，殼長、殼高、殼寬與體質量間的相關系數從大到小依次為殼長＞殼高＞殼寬，而殼長、殼高和殼寬與軟體質量之間的相關系數從大到小依次為殼長＞殼寬＞殼高。總體來看，殼長對體質量和軟體質量影響最大，殼寬、殼高對體質量和軟體部重的影響各不相同。總體來說殼高殼寬影響差異不是很大。

表2 縊蟶各性狀之間的相關系數

2.3 表型性狀與體質量、軟體部重之間的回歸分析

采用逐步回歸法，使保留的各自變量的偏回歸系數檢驗結果均達到極具統計學意義水平（表3）。進而分別得到各表型性狀對縊蟶體質量、軟體部重的最優多元回歸方程如下。

式中，Y1為體質量，Y1為軟體質量，X1為殼長，X2為殼寬，X3為體高。

從表4方差分析結果可以看到，以上兩個方程的回歸關系也都達到了極具統計學意義水平 （P＜0.01），從這兩點表明所求的多元回歸方程成立，這說明進行通徑分析確實是有重要意義的。通過上述方程，也客觀地反映出了縊蟶表型性狀與重量性狀間存在的真實關系。

表3 縊蟶表型性狀的偏回歸系數檢驗

表4 縊蟶表型性狀與重量性狀間多元回歸方程的方差分析

2.4 主要表型性狀對縊蟶體質量、軟體部體質量影響的通經分析

經過2.3回歸分析，保留達到極具統計學意義水平的自變量，再應用SPSS 17.0軟件得到各主要表型性狀對體質量、軟體部重的通徑系數（表5、表6）及相關指數。通徑分析可用于分析多個自變量與因變量之間的線性關系，是回歸分析的拓展，可以處理較為復雜的變量關系。通徑系數反映的是自變量對因變量的直接影響。從表5可知，殼長對體質量的直接作用大于殼高對體質量的直接作用大于殼寬對體質量的直接作用。殼長對體質量的直接通徑系數為0.668，是最大的。殼長通過殼寬、殼高這兩個性狀，對體質量有不同程度的正向間接作用，然而間接作用小于直接作用。因此，殼長是影響體質量的最主要因素。殼寬、殼高對體質量的直接作用較小，但兩者通過殼長對體質量的間接影響作用都較大，這說明著重對縊蟶殼寬、殼高這兩個方面的選擇，有助于增加體質量。

表5 縊蟶表型性狀對體質量影響的通徑分析

由表6可知，殼長對軟體部重的直接作用大于殼寬對軟體部重的直接作用大于殼高對軟體部重的直接作用。殼長對軟體部重的直接通徑系數為0.553，是最大的；殼長通過殼寬和殼高對軟體部重有不同程度的正向間接作用，間接作用小于直接作用。因此，殼長也是影響縊蟶軟體部重的重要因素之一。殼寬和殼高對軟體部重的直接作用都小于其對軟體部重的間接作用，二者通過殼寬對軟體部重的間接影響效應都較大，尤其是殼高主要通過間接作用對軟體部重產生影響。

表6 縊蟶性狀對軟體部重影響的通徑分析

2.5 主要表型性狀對體質量、軟體部重的決定程度

將縊蟶形態性狀與活體質量的相關系數分為直接作用和間接作用兩部分，即各表型性狀的直接作用和對其他性狀的間接作用。計算各單一表型性狀及性狀間協同作用對重量性狀的決定系數（決定系數公式），計算出的結果參見表7、8。殼長、殼寬和殼高對體質量的相對決定程度是44.60%、3.0%和1.0%（見表 7）；殼高、體高和厴長對軟體部重（Z）的相對決定程度是30.6%、5.60%和0.70%（見表8），從表中可以看到殼長對體質量和軟體部重的決定程度都最大，其次是殼高和殼寬，并且各有不同。從共同決定系數可以看出，殼長、殼寬二者對體質量和軟體部重的共同決定程度分別為18.70%和18.30%。進一步分析，各表型性狀對體質量、軟體部重的決定系數的總和分別為Σdxy=0.8110和0.6510（見表7、8）；它們分別與對應的相關指數R2的數值相等，結果表明表中所列各性狀是影響縊蟶體質量和軟體部重的主要性狀，其他性狀的影響程度相對較小。

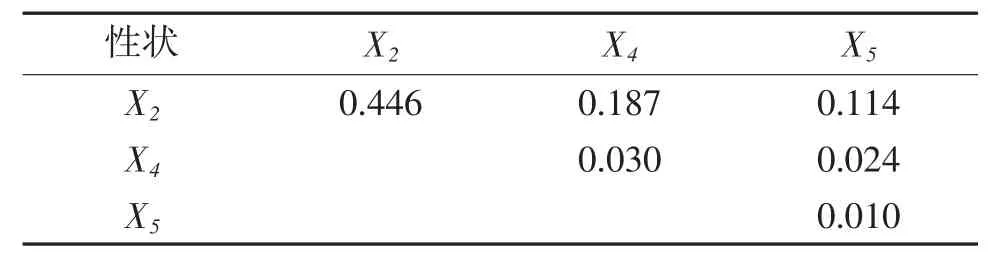
表7 縊蟶表型性狀對體質量的決定系數

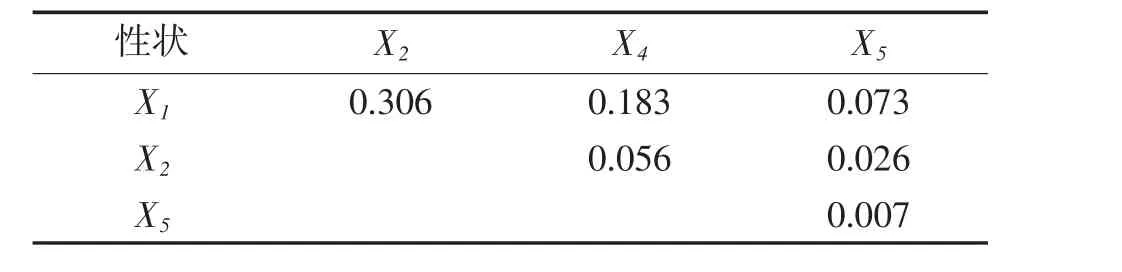
表8 縊蟶表型性狀對軟體部重的決定系數

3 討論

3.1 縊蟶的測度指標

貝殼類貝殼形態的測度指標主要有3項，分別是殼長、殼寬、殼高。該文引入了這3項參數可以在一定程度上直觀地反映出縊蟶貝殼的膨脹程度[9]。從該文得出的貝殼表型性狀對體質量的多元回歸方程 Y1=-16.199+0.326 X1+0.254 X2+0.149 X3，以及對軟體部重的多元回歸方程，Y2=-9.723+0.179 X1+0.230 X2+0.076 X5。通過兩項參數反映出貝殼表型性狀與重量性狀的關系，可以作為縊蟶的測度指標。數量遺傳研究領域的科研工作者們一直關注多個數量性狀之間的關系。在貝類人工育苗過程中親本的選擇是非常關鍵的。親本的選擇通常從體質量、軟體部重和形態性狀等這幾項指標作為重要依據，體質量是最直接的目標性狀。從縊蟶殼形態性狀對重量性狀的通徑分析，可以從多個形態性狀中找到影響重量性狀的主要因素，研究結果將對縊蟶的育種選擇提供重要理論依據。

3.2 各主要性狀對體質量、軟體部重的作用

通徑分析的特點是把自變量與因變量的相互關系，分為直接作用和間接作用，即自變量對因變量的直接作用，以及自變量通過其他自變量對因變量的間接作用。從文中數據分析可得，殼長對縊蟶的體質量、軟體部重而言，都是影響最大的參數，殼長對體質量、軟體部重的直接作用均大于間接作用，因此可以用殼長來判斷體質量和軟體質量，同時也可看出殼長的參數數據對縊蟶的增養殖的重要性。再分析剩下的2個參數數據，很容易看出，其中殼高對體質量的直接作用大于殼寬對體質量的直接作用，但二者的直接作用均小于其間接作用（見表5），表明它們主要通過殼長的間接效應來影響體質量。殼寬對軟體部重的直接作用大于殼高對軟體部重的直接作用，同樣二者對軟體部重的間接作用都大于其直接作用（見表6），表明它們對軟體部重的貢獻主要也是通過殼長的間接效應，并且對于體質量和軟體部重來說，殼寬和殼高的影響是不同的。通過該文數據顯示決定系數分析與通徑分析的結果變化趨勢是一致的。綜上所述，殼長是影響縊蟶的體質量和軟體部重的最主要表型性狀。殼高和殼寬對重量性狀的間接影響效應都較大，是不容忽視的主要表型性狀，在縊蟶選擇育種中，從這3個性狀進行參比選擇，將增加縊蟶的體質量和軟體部重[15]，從而增加縊蟶的產量與質量。在其他有關雙殼貝類的通徑分析中，貝類種類的不同，相同參數影響效果也不同。例如櫛孔扇貝殼高對其軟體質量的影響最大，蝦夷扇貝殼寬對閉殼肌重的影響最大，紫石房蛤殼寬對活體質量的影響最大，青蛤殼高對軟體部重的影響最大,可見對雙殼貝類重量性狀影響最大的主要因子不一定是殼長，有時往往是殼高或殼寬。

3.3 決定縊蟶體質量、軟體部重的主要構成因子

該試驗統計了縊蟶的各表型性狀的數值，數據顯示生長性狀均存在一定程度的變異，為選種提供了大量的基礎材料。從表型性狀統計中，不難發現不同年齡縊蟶的形態性狀和重量性狀的變異程度有所不同[10-11]。通過計算縊蟶殼長、殼高、殼寬、活體質量、軟體部重的相關系數結果看出各性狀相關系數均達到極具統計學意義水平[12-13]。如果自變量對因變量的相關系數達到具統計學意義水平，自變量就可以被選為通徑分析的條件，縊蟶各表型性狀都可以進一步做通徑分析。經過通徑分析，縊蟶表型性狀對軟體部重的相關指數與決定系數總和的數值（大于0.85）近似相等，這就進一步說明殼長、殼寬和殼高是影響各重量性狀的重點性狀。這與一些學者對櫛孔扇貝（Chlamys farreri）、長肋日月貝（Amusiumpleuronectes）、蝦夷扇貝（Patinopecten yessoensi）、大扇貝（Pecten maximus）、紫石房蛤（Saxidomus purpurat us）的研究結果一致。該研究結果證實了影響縊蟶體質量、軟體部重的主要影響因子，對今后指導縊蟶的選擇育種有重要的理論意義。在實際工作中也可以依據隨機抽樣測量的殼長、殼寬、殼高，利用上述回歸方程，估算出縊蟶的體質量或軟體部重[14]。

該研究是試圖找出影響縊蟶體質量和軟體部重的主要體形性狀，通過相關分析、通徑分析和多元回歸分析，建立多元回歸方程，明確了縊蟶殼長、殼高和殼寬3個性狀與重量性狀的關系，為縊蟶育種工作提供了理論依據和重要參考指標[16]。