多因素影響貢獻度視角下礦產資源開發利益分配研究

魏 帥，黃光球，聶興信

(西安建筑科技大學 管理學院，陜西 西安 710055)

目前，關于礦產資源開發利益分配問題，國內外學者多從稅費制度和利益博弈兩個角度進行了研究。張炎治，魏曉平[1]認為資源稅費制度的設計缺陷是導致政府和企業資源利益分配錯位的根本原因。陳占鋒[2]認為礦產資源開發利益相關者存在一種不合理的利益格局。王小萍[3]從法律角度認為應重構礦產資源利益公平分配法律制度體系。周丹，熊華丹[4]認為應重點對礦產資源補償費和資源稅進行改革。王承武[5]認為必須建立礦產資源開發利益分享機制。劉春學，李連舉[6]利用博弈理論和方法，構建了礦產資源開發企業和礦區居民之間的不完全信息動態博弈模型。傅建球，徐運保[7]指出了農村礦產資源開發中存在的利益分配扭曲問題。文獻[8]從政府制定政策的角度實現礦產資源利益的合理分配。相關研究多是基于分配制度、調整對策等方面展開研究，對合理改進礦產資源開發利益分配體系具有較好的促進作用。但如何量化礦產資源開發各利益相關方之間的利益分配，有效解決利益分配不均及利益沖突問題，還有待深入研究。

1 相關理論文獻綜述

Shapley值法是由美國對策論專家LloydShapley提出的解決多人合作對策模型，常用于解決利益分配問題。徐秋爽，穆麗運用Shapley值法解決配送問題的利益分配。盛松濤考慮到合作成員貢獻度對利益分配的影響。付秋芳構建了一個更合理的Shapley-RIEP模型。國外學者Yoshio Kamijo對Shapley值法成本分攤模型進行改進。Conrado Manuel考慮了合作博弈中中立人員對Shapley值利益分配的影響[9]。綜上，Shapley值法沒有考慮各種影響因素對利益分配的影響，實際應用中需考慮各因素建立權重體系對Shapley值分配結果進行修正，使分配結果更符合實際情況更合理。

本文的研究思路是：首先界定礦產資源開發核心利益相關者，制定礦產資源開發利益分配準則，然后構建核心利益相關者合作博弈與Shapley值法模型。本文的特色之處是：綜合考慮礦產資源開發利益分配的影響因素，運用熵權法和理想點原理，對傳統的Shapley值的利益分配模型進行修正，結合礦產資源開發實際案例優化利益分配策略。

2 礦產資源開發核心利益相關者界定

依據Freelman關于利益相關者的概念[10]，根據在礦產資源開發中發揮的作用和利益相關的程度不同，把利益相關者分類(見表1)。在企業為責任主體、經營主體、受益主體的傳統礦產資源開發模式下，政府、礦業企業、礦區居民是礦產資源開發的核心利益相關者，本文提出政府、礦業企業、礦區居民三方聯合進行礦產資源開發的“屬地聯席”新模式，即“政府有償出讓礦產資源，礦業企業主體經營開發，礦區居民直接有效參與開發，三方共同參與經濟利益分配”模式。核心利益相關者是是本文的研究對象，其在追求自身利益時，會產生利益沖突，而確保礦產資源開發順利實施的關鍵在于制定科學合理的經濟利益分配策略。

表1 礦產資源開發的利益相關者

基于互利共贏、收益與投入、風險相對稱、公平兼顧效率的原則進行礦產資源開發利益分配。

3 合作博弈模型及Shapley值法利益分配模型構建

礦產資源開發及利益分配問題，可視為政府、企業企業、礦區居民三方進行合作博弈的問題。合作博弈由局中人集合和特征函數這兩個基本要素構成[11]。局中人集合由對礦產資源開發過程有影響的獨立利益主體構成，這個集合中的元素稱為局中人[12]。假設某礦產資源開發中有n個利益主體，用集合N={1，2………n}表示，每一個利益主體看作一個局中人。本文把礦產資源開發利益相關者合作后取得的總收益定義為特征函數[13]。

設集合N={1，2……n}，如果對于N的任意子集S都對應一個實值函數V(S)，滿足V(Φ)=0，利益相關方不相互合作時，不會取得收益。V(S1∪S2)≥V(S1)+V(S2)(其中S1與S2相交為空集)，利益相關者合作獲得的收益大于不合作獲得的收益。此時稱[N，V]為n人合作對策，V為對策的特征函數[14]。

Shapley值法是沙利提出的用于解決多人合作對策問題的一種數學模型。設合作博弈的集合I={1，2………}，對于其子集S對應一個函數V(S)，第i位合作伙伴從聯盟中獲得的收益為φi，公式如下：

[v(s)-v(s/i)]，(i=1，2……n)

(1)

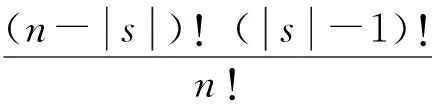
4 基于熵權法的Shapley值修正

4.1 考量多重因素影響貢獻度的Shapley值修正分析

Shapley值考慮到了各成員對合作的邊際貢獻，避免了平均分配的弊端，但是默認各成員風險分擔均等，都為1/n，但實際上在礦產資源開發的過程中，各成員風險分擔、投資比重、自身的創新能力、任務執行度各不相同，而且對礦產資源開發的利益分配有重要影響。需要綜合考慮多種因素，對Shapley值進行調整。因為礦產資源開發利用具有風險高的特點[16，17]。關于風險因素評價指標本文在前人研究基礎上從技術風險、企業能力風險、市場風險、其他風險幾個方面進行評價[18]，見表2。礦產資源開發過程中需要投入很多資金人力物力[19]，礦產資源開發利益相關者具備創新能力[20]。本文借鑒《基于競合策略的供應鏈風險及收益分配分析》關于創新能力的相關指標，見表3。任務執行度體現各利益相關者在礦產資源開發過程中，對各類任務指標的執行程度[21]。

表2 礦產資源開發風險評價指標

表3 礦產資源開發成員創新能力指標

考量以上多重因素對礦產資源開發的影響及貢獻度，建立基于多重因素影響及貢獻度的Shapley值修正模型，如圖1所示。

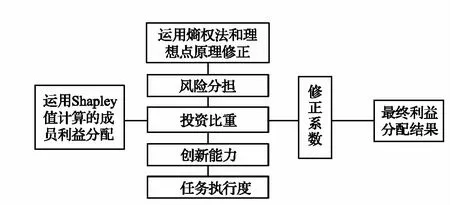
圖1 基于多重因素影響及貢獻度的Shapley值修正模型

4.2 基于熵權法的Shapley值修正

本文采用客觀的熵權法確定權重。

4.2.1 修正矩陣計算與處理

參考孫世民[22]的研究建立如下模型：設礦產資源開發利益分配修正因素集合為J={1，2…n}，第i個成員關于第j個修正因素測度值為aij(i=1，2…m，j=1，2…n)，修正矩陣為A=(aij)m×n。進行如下規范化處理：

規范化后的利益分配矩陣為B=(bij)m×n。

4.2.2 修正權重的確定

采用熵權法計算修正權重[23]。設有m個成員，n個修正因素(評價指標)，第j個指標下對應指標比重為Pij，

第j個指標的熵值為：

第j個指標的權重為：

4.2.3 修正系數的確定

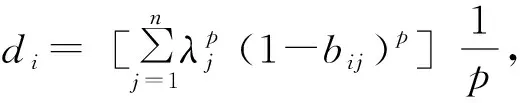
5 實例研究

收益分配主體是指在某種前提條件下獲得相應份額利益的社會群體或團體，主要有政府，企業，礦區居民[26]。根據進行收益情況調研及并對歷史開發所收集相關數據的進行整理，得到下表數據，各成員單獨和組合開發的利益分配情況分析已知。政府，礦業企業，礦區居民分別用1，2，3分別表示，單獨和組合開發的利益分配情況見表4。Shapley值法利益分配額的確定和計算過程如下：

表4 利益分配表(萬元)

注：數據選自 《基于Shapley值法的礦產資源開發利益相關者利益分配博弈分析》的計算。

表5 利益相關者政府的利益分配值

由Shapley值模型計算可得，政府的利益分配值為：φ1(v)=100/3+200/6+160/6+240/3=173(萬元)，同理可得企業的利益分配值φ2(v)=93(萬元)，礦區居民利益分配值φ3(v)=54(萬元)。通過向礦業領域專家發問卷，請專家從風險分擔、投資比重、創新能力、任務執行度幾個方面對政府，礦業企業，礦區居民三方對進行評價，得到各修正因素的測度值，修正因素的基礎數據見表6。

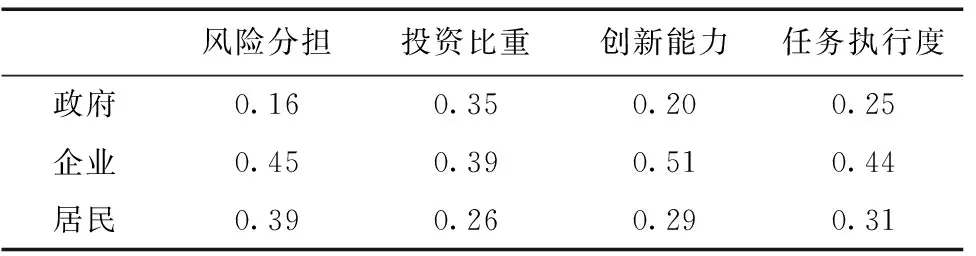
表6 修正因素的基礎數據

運用熵權法計，據上文公式算各修正因素的熵值和權重見表7。

根據上述公式和方法計算修正系數和修正額見表8。

修正結果表明，修正后的利益值仍然比三方核心利益相關者單獨開發礦產資源所獲得的收益要大，符合合作開發的參與約束前提條件。由于政府擁有的自身資源優勢，單純從貢獻度角度，獲得了較大收益。綜合考慮幾個修正因素以后，政府由于體制原因，不能承擔太大風險，創新能力有限，而企業屬于風險偏好型，善于應對市場變化，勇于創新，居民承擔環境破壞等較多風險，企業和居民利益分配有所增加，政府利益分配有所減少。

表8 修正過程計算結果統計表

6 結 語

考慮到各合作成員的風險分擔，投資比重、創新能力和任務執行度因素，計算出各因素的熵值和權重，并計算出各成員的修正系數，對傳統Shapley值法利益分配進行修正。采用多因素視角下考慮貢獻度的利益分配方式，應用在礦產資源合作開發利益分配中，對各方原有利益分配額度進行調整優化，使利益分配更加科學合理，能對利益相關方起到更好的激勵作用，為礦產資源開發利益分配提供了方法借鑒。但是運用該方法也存在不足，需要測算成員在各種合作組合情況下的收益值，以確定各成員的邊際貢獻值。