基于工作負荷的現代有軌電車行車調度崗位設置研究

羅 文 唐光華

(廣州有軌電車有限責任公司， 510030， 廣州//第一作者，工程師)

隨著現代有軌電車的飛速發展、網絡化運營的不斷完善，控制中心管轄的列車也隨著增多。當調度任務量極速增長時，行車調度員可能會出現反應遲緩、錯誤操作的情況，給列車運營帶來安全隱患。反之，調度任務量過少，行車調度員也會出現注意力不集中、單調乏味的現象，不僅降低工作績效，還會引起行車調度配員的增加，導致成本上升、資源浪費。

因此，適當的調度工作量關系到生產效率、行車組織的安全性。為了保證列車運行安全、優化調度資源，對行車調度崗位人員的合理配置就尤為重要。

1 調度崗位工作負荷建模

1.1 調度的工作負荷定義

從人因工程學來看，行車調度崗位人員的配置應使行車調度員的工作負荷之和滿足其業務負荷的需求。工作負荷是一個多維度的概念，其影響因素包括崗位要求、任務輕重、時間緊迫感，以及執行者的能力高低、努力水平和具體的個人經驗。本文將工作負荷定義為在單位時間內完成職責任務所需的時間占比。即：

θ占=t任/t評

式中：

θ占——時間占比；

t任——評估期內的工作耗時；

t評——評估期內總耗時。

英國鐵路和標準化局根據θ占將工作負荷劃為三級，如表1所示。

表1 英國鐵路工作負荷等級劃分標準

1.2 調度工作負荷分類

評估行車調度員的工作負荷有3種方法：① 主觀評估法，即通過檢查行車調度員的主觀感覺來評估；②任務分析法，即通過檢查行車調度員的工作量來評估；③ 生理測量法，即通過檢查行車調度員的生理變化來評估。

本文使用任務分析方法來研究行車調度員工作負荷。任務分析法將行車調度工作分為看得見的工作(臺賬填寫，操作列車監控系統和通信協調等能夠被記錄和記時的工作) 、看不見的工作(監控運營列車、思考行車組織計劃等不便于記錄和記時的工作)和恢復工作(確保平均工作負荷強度低于80%的臨界值)。

按照任務分析法，調度任務的全面分析需采用視頻搜集和數據梳理兩種方式，按照責任、任務和動作3個層次，來匯總和提煉調度執行的所有工作，從而獲得調度的基本任務集。將調度工作的所有作業任務映射到基本任務集，即可得出了6類行車調度工作負荷子集。即將調度工作負荷分為監視負荷、思考負荷、操作負荷、記錄負荷、通信負荷及其他負荷。

1.3 全日工作負荷評估及分析

本文以廣州現代有軌電車行車調度的實際工作為例，搜集并整理了各類調度工作負荷對應的工作。首先，連續1周以24 h為周期，跟蹤觀察行車調度員的操作、通信、臺賬和視頻回放等工作記錄，以采集白班和夜班作業的所有內容(具體工作內容見表2)；然后，按單位小時計算θ占，求出每1 h時間段內的θ占平均值，最終得到調度工作負荷24 h評估結果(見圖1)。

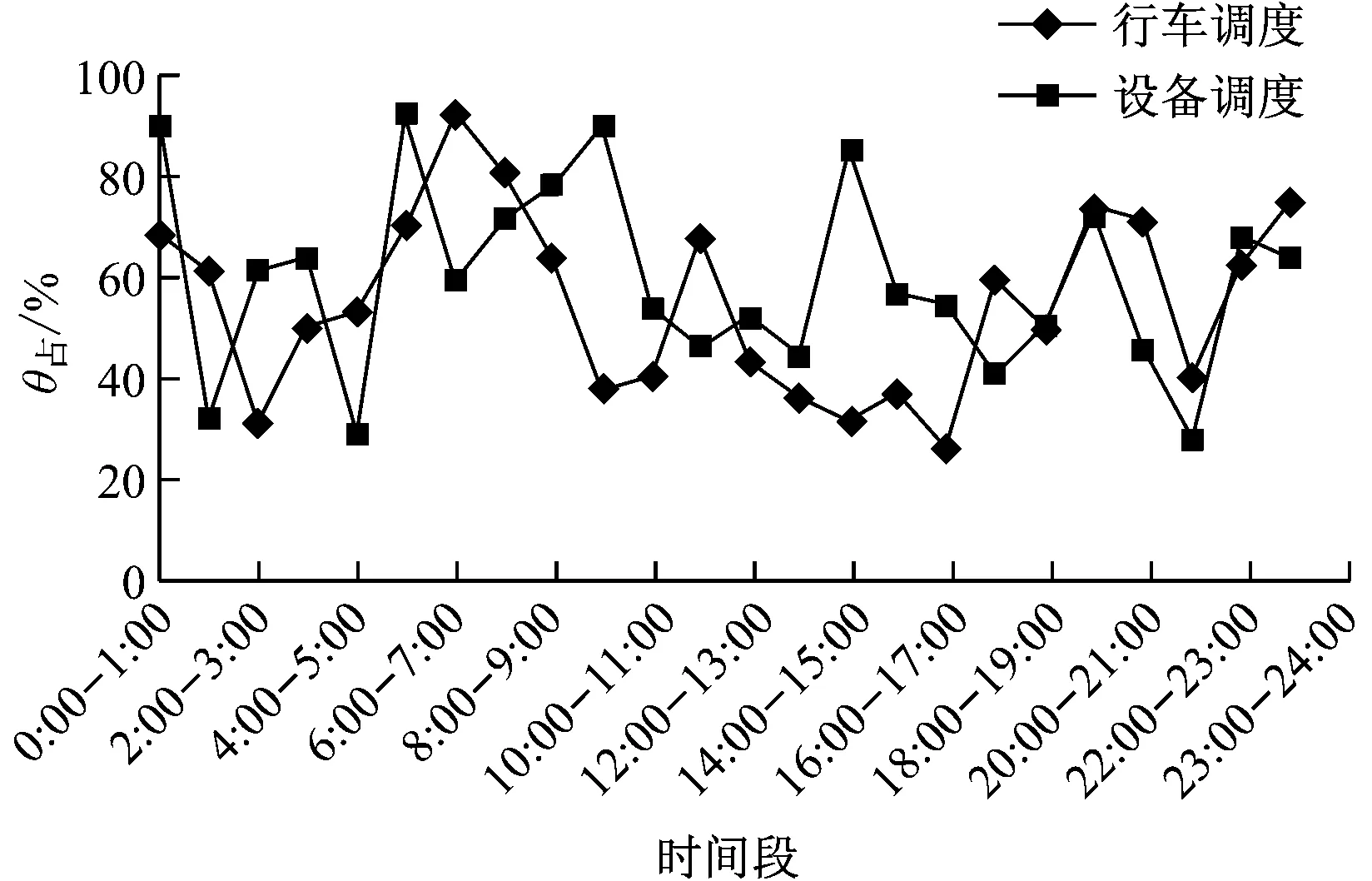
圖1 連續一周調度工作負荷24 h評估結果

由圖1可以看出，全天24 h行車調度的工作負荷呈現出一定的波動趨勢。其中，行車調度工作最大負荷集中在早上運營前的檢查、出車時段。

2 基于行車調度工作負荷的崗位配置計算

行車調度員的工作負荷與其管轄范圍內的行車量密切相關。若行車調度員的工作負荷達到飽和狀態的臨界值，而列車數卻進一步增加，則會超出行車調度員的組織能力范圍，增加行車安全風險。此時的線上行車數量即為飽和量。

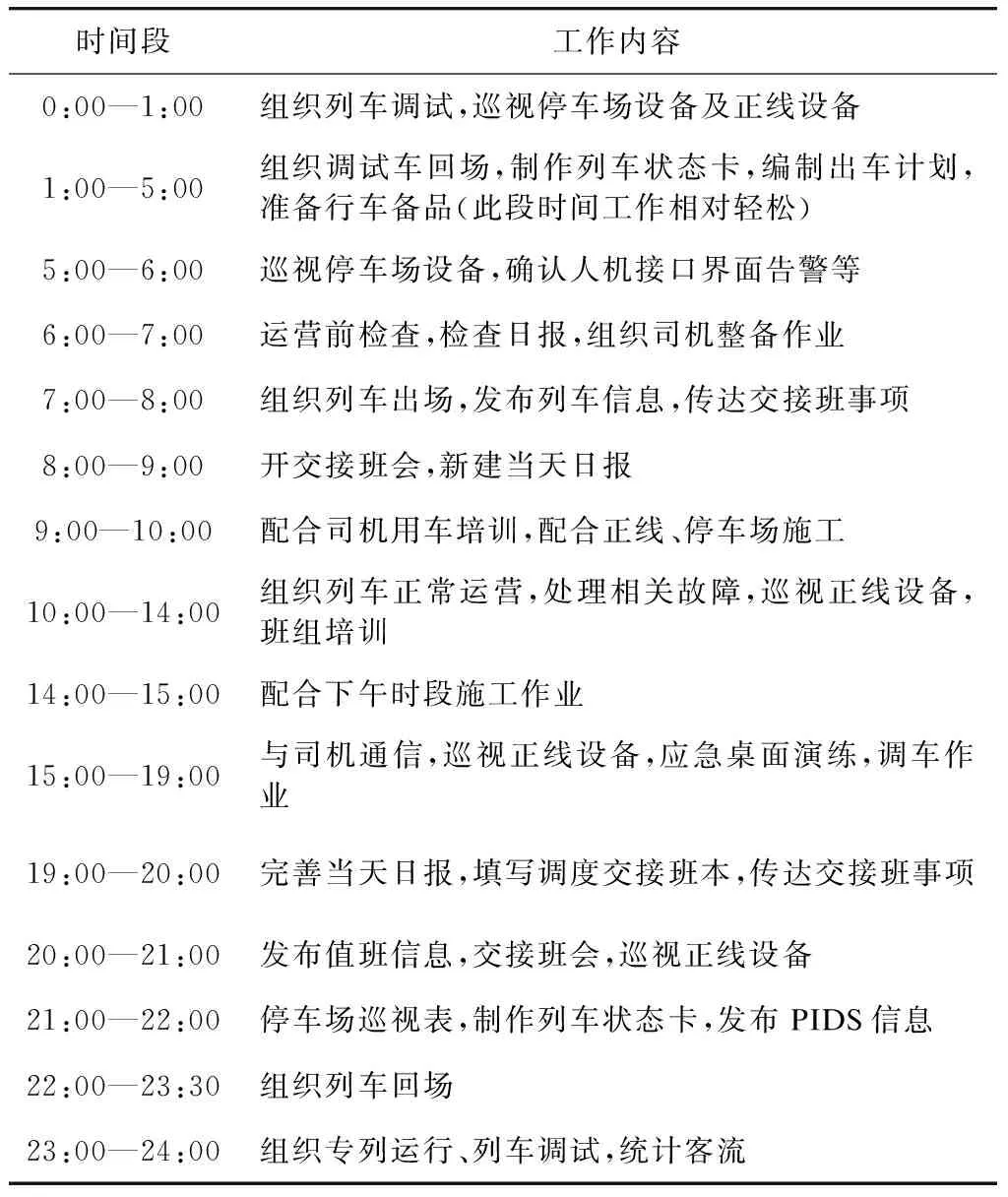
表2 行車調度員在各時間段的具體工作內容

基于行車調度工作負荷的評估，則可計算列車飽和量。通過量化評估行車調度員的日常工作負荷，可以全天候隨時了解行車調度員的工作負荷狀況，判斷其工作忙閑程度的時間分布，并以此評估列車飽和量。

2.1 相關變量的選取

上線列車數與行車調度工作負荷密切相關。有軌電車的行車調度工作涉及到有軌電車出入場、折返、進出存車線及存車線備用等多種工況。有軌電車運轉流程圖如圖2所示。正常情況下，有軌電車可根據預設的目的地碼自動排列進路，按照運營時刻表行車。此時，行車調度員的工作是監控列車運行。但在非正常情況下，如因列車設備故障、列車沖突及交通事故等突發事件，而造成列車抽線、晚點、中斷運營或改變列車運行交路時，需行車調度員人工介入進行調整。此種情況則賦予了行車調度員新的工作任務，增加了相應的工作負荷。可見，人工調整列車亦與行車調度員的工作負荷密切相關。

綜合考慮，為研究行車調度員的工作負荷與運營列車之間的相互關系，初步確定行車調度員的工作負荷同運營列車數及人工調整列車數有關。在一定評估期內，工作負荷由工作耗時確定。因此將行車調度工作耗時設為因變量，將運營列車數和人工調整列車數設為自變量，并篩選適當的方法進行求解。

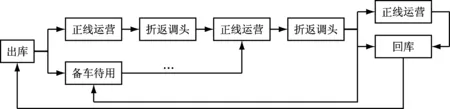
圖2 有軌電車運轉流程圖

2.2 建立行車調度員工作負荷回歸模型

2.2.1 采集變量數據

基于對行車調度員工作負荷的定量分析，結合廣州有軌電車的實際運營時間，確定因變量及自變量。首先，確定評估期為為7:00—22:00，共15 h；然后，按運營列車數，分別統計同時上線4列、5列、6列有軌電車時的調度工作耗時；最后，確定不同人工調整列車數對應的調度工作耗時。對于人工調度列車數，本文只統計列車故障下調整的列車數。

2.2.2 繪制散點圖

根據統計的數據進行整理，得到運營列車數、人工調整列車數對應行車調度工作耗時的散點圖，如圖3～4所示。

2.2.3 回歸方法的選擇

通過散點圖可以看出，自變量與因變量間呈現明顯的線性正相關關系，且自變量間高度不相關。因此，選擇多元線性回歸分析進行求解，由此建立二元回歸模型為:

y=β0+β1x1+β2x2+ε

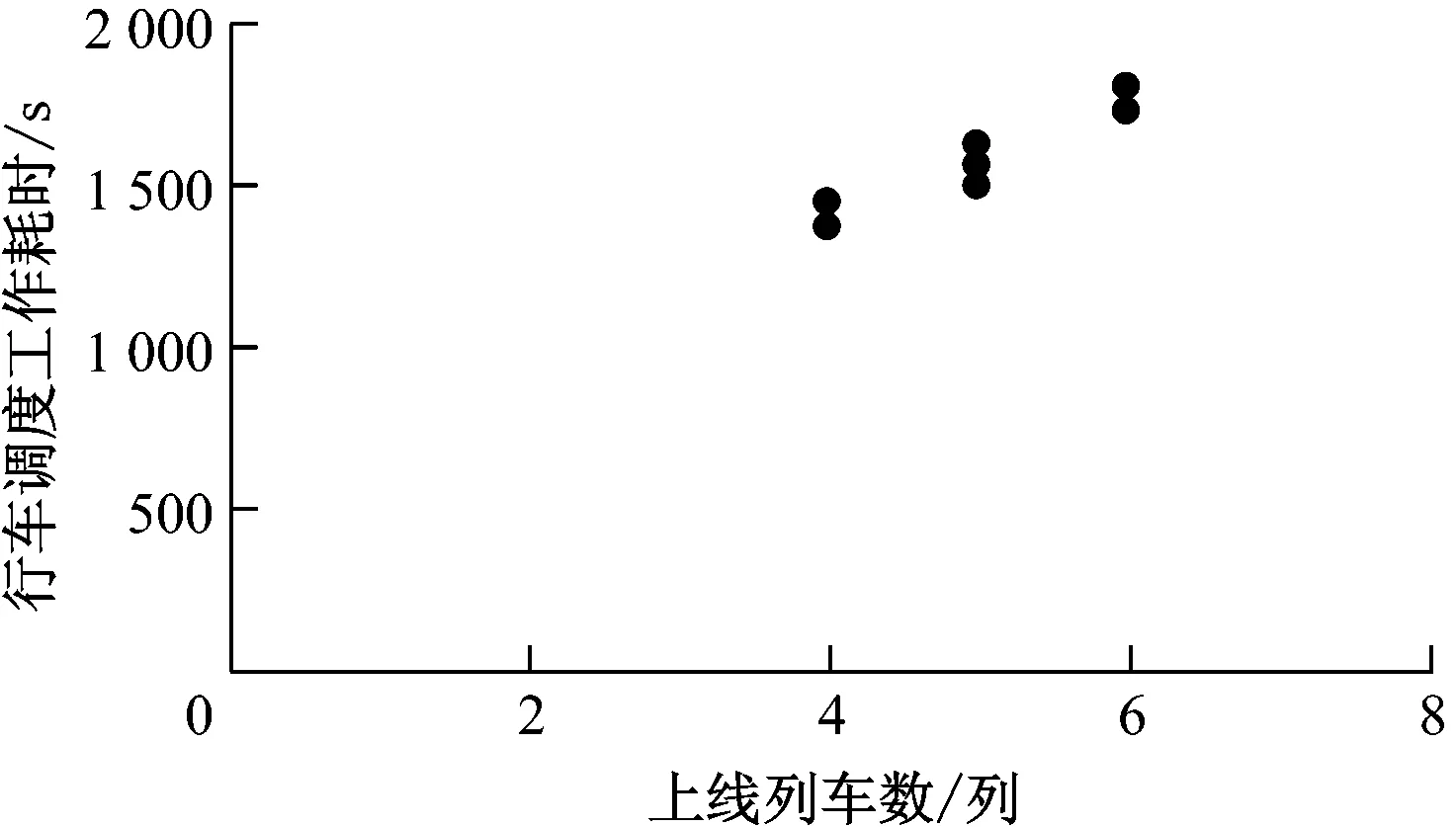
圖3 不同上線列車數對應的行車調度工作耗時

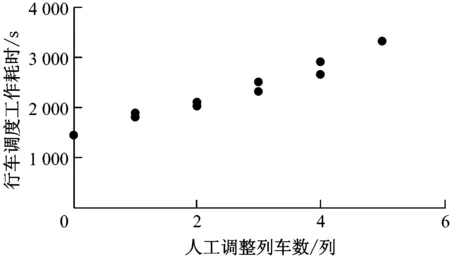
圖4 不同人工調整列車數對應的行車調度工作耗時

式中：

y——工作耗時；

x1——運營列車數；

x2——人工調整列車數；

β0——回歸常數；

β1,β2——分別為x1,x2的回歸常數；

ε——隨機誤差項。

根據統計數據，進行多元線性回歸分析。分析結果如圖5所示。

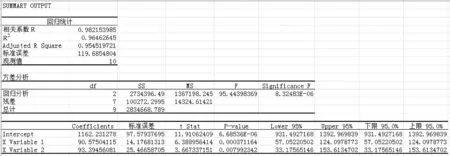
圖5 工作負荷線性回歸分析參數

根據圖5中顯示結果，相關系數R為0.982，說明上線列車數和人工調整列車數同行車調度工作耗時呈現高度正相關。故可用二元線性回歸方程進行擬合。計算得到的行車調度工作耗時回歸方程為：

y=90.58x1+93.39x2+1 162.23

其中，y單位為s，x1、x2單位為列。

計算得到判定系數等于96.46%。這表明在行車調度工作負荷變動中，有96.46%可由上線列車數和人工調整列車數這2個因素的變動來解釋，只有3.54%的因素屬隨機誤差。

設顯著性水平α=0.05，查F分布表得F0.05(2，7)=4.74。計算得到F=95.44>4.74。因此，拒絕原假設，認為y同x1及x2有顯著的線性關系。

從圖6可見，所有的殘差都在0附近均勻分布，且區間幾乎都位于[-200 s, 200 s]之間，沒有發現高杠桿點。即數據中沒有強影響點或異常觀測點。

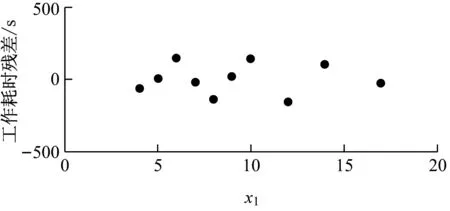
a) x1變化時

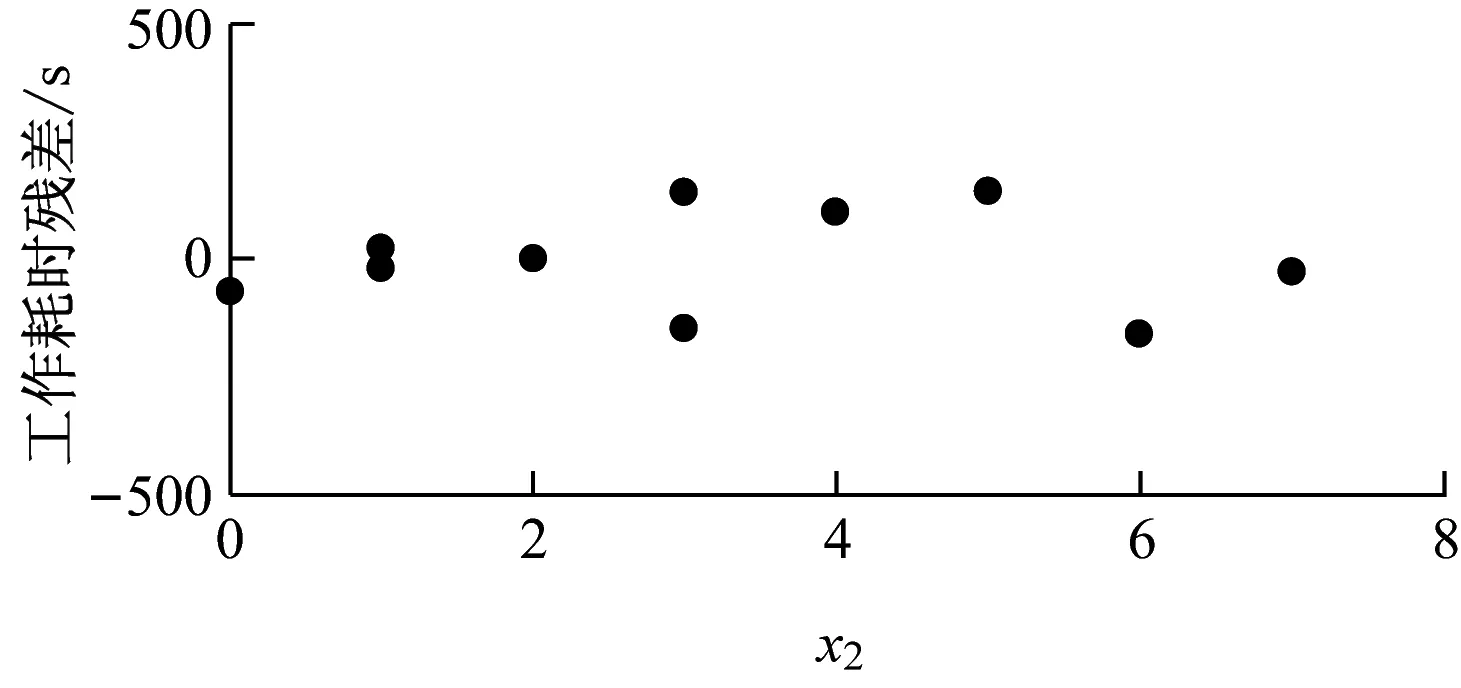
b) x2變化時

故認為行車調度工作耗時回歸方程是整體顯著的。

其次，設α=0.05，β1的檢驗統計量t1=6.39、β2的檢驗統計量t2=3.67，查t(檢驗統計量)分布表得t0.025(7)=2.36。因t1、t2均大于t0.025(7)，因此，拒絕原假設，認為行車調度工作負荷回歸模型的各個回歸系數是顯著的。

3 結語

本文以廣州現代有軌電車為例，系統分析了現代有軌電車行車調度的工作任務，借用任務分析方法建立了行車調度工作負荷模型，并進行了量化測量，以此評估行車調度的工作負荷狀況。在此基礎上尋找影響行車調度工作負荷的自變量，建立了多元線性回歸模型，并校驗了模型的準確性，對現代有軌電車行車調度崗位配員和新線規劃具有一定的參考意義。