基于混合蛙跳優化的采摘機器人相機標定方法
陳科尹 鄒湘軍 關卓懷 王 剛 彭紅星 吳崇友
(1.農業農村部南京農業機械化研究所, 南京 210014; 2.賀州學院信息與通信工程學院, 賀州 542899; 3.華南農業大學南方農業機械與裝備關鍵技術省部共建教育部重點實驗室, 廣州 510642)
0 引言
相機標定是采摘機器人進行視覺識別與定位的重要前期步驟之一。相機標定精度在很大程度上決定了后續目標識別定位的準確性。因此,找到一種精度高、穩定可靠的相機標定方法顯得格外重要。目前,比較常見的相機標定方法是基于張正友相機標定原理,利用計算智能優化算法對其進行改進[1-7]。YAO等[1]利用遺傳算法BP神經網絡對張正友相機標定方法進行改進;FüHR等[2]在張正友相機標定方法的基礎上,提出了一種基于非線性優化的相機自標定方法;PITCHANDI等[3]結合張正友相機標定方法,利用遺傳算法對視覺輔助機器人裝配系統的相機標定問題進行了研究;ZHANG等[4]基于張正友相機標定方法,提出了一種基于線段的柔性在線相機標定方法;游江等[5]提出了基于改進遺傳模擬退火的相機標定方法;柯豐愷等[6]提出了基于凸松弛優化算法的相機內外參數標定方法;劉艷等[7]針對魚眼鏡頭存在的畸變問題,對張正友相機標定法進行了改進。
但此類基于張正友相機標定原理改進的相機標定方法還存在以下問題[8-9]:在求取相機標定參數初值時,先不考慮相機畸變因素,直接利用平面靶標圖像中的特征點線性求解相機標定參數初值。但實際上這些特征點存在的畸變誤差會影響相機標定參數初值的準確性。在考慮相機畸變因素、進一步優化相機標定參數時,采用了非線性優化過程,若相機標定參數初值選擇不當,容易收斂到局部最小,從而影響相機標定參數的精度以及穩定性。平面靶標圖像數量直接影響相機標定參數的精度和穩定性。基于張正友相機標定原理的本質是通過建立平面靶標圖像中特征點的世界坐標與像素坐標之間的映射關系方程組,根據最小二乘方法,求取相機標定參數。顯然,通過增加平面靶標圖像數量,即可增加特征點的世界坐標與像素坐標之間映射關系方程組的數量,從而提高最小二乘方法求取相機標定參數的精度。但隨著平面靶標圖像數量的不斷增加,在同等標定環境下特征點的提取和畸變等誤差也不可避免地帶入相機標定過程,從而影響相機標定參數的精度和穩定性。
為此,按照對采摘機器人相機標定精度的要求(相機焦距的絕對誤差在0.1~1 mm內,相對誤差在1%~15%內;平面靶標圖像特征點的平均像素誤差在1個像素內;雙目相機之間距離的絕對誤差在1~5 mm內,相對誤差在1%~6%內),本文擬引進混合蛙跳優化算法和LM算法對采摘機器人相機標定,進行定量研究。同時,為驗證本文相機標定方法的有效性和可靠性,分別同傳統張正友相機標定方法(OpenCV庫自帶)、基于遺傳算法的相機標定方法以及基于標準混合蛙跳算法的相機標定方法進行相機標定性能對比試驗。
1 相機標定
1.1 張正友相機標定原理
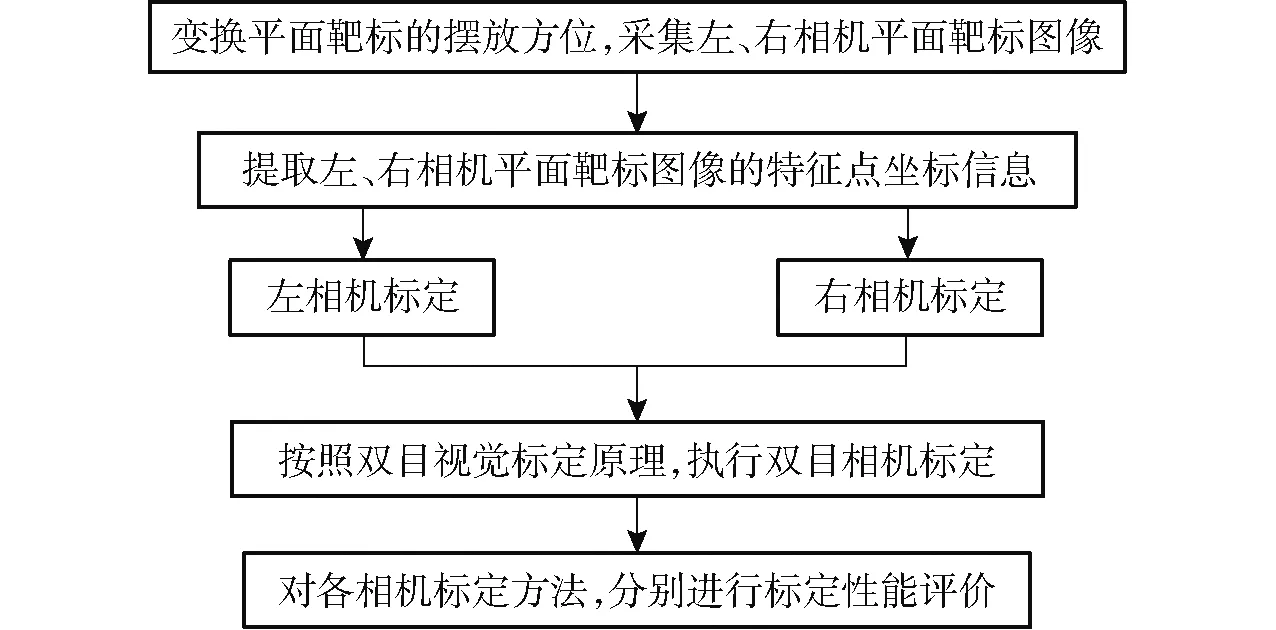
張正友相機標定原理[10]是通過移動相機或平面靶標(標定板),從不同的方位采集平面靶標圖像,利用平面靶標上特征點的圖像坐標和其已知的三維空間坐標(Z坐標置為0)的對應關系,計算出相機模型參數的初始值,然后再進行非線性優化,從而完成相機標定操作。其具體相機標定過程如圖1所示。
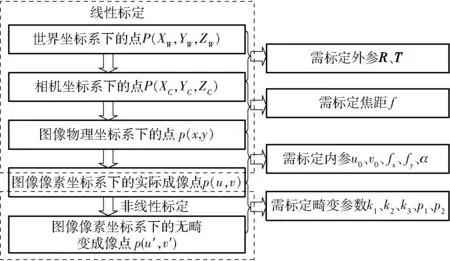
圖1 張正友相機標定原理的相機標定過程Fig.1 Camera calibration process with Zhang Zhengyou’s camera calibration principle
圖1中,R為相機外參旋轉矩陣,T為相機外參平移向量,f為相機焦距,u0為相機內參光心橫向像素坐標,v0為相機內參光心縱向像素坐標,fx為相機內參焦距橫向像素,fy為相機內參焦距縱向像素,α為相機內參成像平面傾角,k1、k2、k3為相機徑向畸變參數,p1、p2為相機切向畸變參數。
1.2 基于改進混合蛙跳算法和LM算法的相機標定原理
張正友相機標定方法,一般先直接求取相機模型的參數初值,然后利用LM算法對該參數初值進一步非線性優化求精,從而求出最終的相機模型參數。但是,直接求解相機模型參數初值的計算過程非常繁瑣,并且由于LM算法自身固有的特點,該類相機標定方法對相機模型的參數初值非常敏感,從而使標定出的相機模型參數很不穩定。
本文結合混合蛙跳優化算法以及LM算法各自的特點,對張正友相機標定原理,進行以下幾點改進:直接運用最小二乘法求取單應性矩陣,不必要利用LM算法對其進行優化,簡化了求取單應性矩陣的過程。運用混合蛙跳優化算法來求取相機模型參數初值,避免直接求取相機模型的參數初值所帶來的繁瑣計算和LM算法對參數初值敏感的問題。運用改進LM算法對相機模型的參數初值進行優化處理,避免了原LM算法必須求取需要優化參數的雅可比矩陣,從而造成優化過程中出現不穩定現象。
1.2.1混合蛙跳優化算法
混合蛙跳優化算法[11-13]是模仿青蛙覓食過程中的群體信息交互機制而建立的一類智能計算優化算法。該優化算法結合了模因(Meme)演算法和粒子群優化算法各自的優點,具有概念簡單、控制參數少、計算量小、全局尋優能力強、魯棒性好、易于實現等特點。為此,選取該優化算法來求取相機模型的參數初始值。其基本原理可描述為:
假設L={F1,F2,…,FN}為N只青蛙組成的初始種群;其中,Fi={xi1,xi2,…,xiS}為所求問題的S維解空間中的第i只青蛙。并且,將該種群內的青蛙個體按適應值降序排列。接著把整個種群劃分為m個模因組,第1只青蛙劃入第1個模因組,第2只青蛙劃入第2個模因組,第m只青蛙劃入第m個模因組,第m+1只青蛙劃入第m+1個模因組,依此類推,直至種群內所有青蛙分配完畢。
同時,把每一個模因組內具有最好適應值和最差適應值的青蛙分別標記為Fb和Fw,而該種群中具有最優適應值的青蛙標記為Fg。然后,對模因組內的每一個青蛙執行局部位置更新操作,具體更新公式為
(1)
式中r——0~1之間的隨機數
D——青蛙移動的距離
?——位置更新操作
Dmax——青蛙所允許移動的最大距離
如果更新后得到的青蛙優于原來的青蛙,則可替代原模因組內的青蛙Fw;否則,用Fg代替Fb,執行局部位置更新操作
(2)
如果式(2)操作仍然不能獲得更好適應值的青蛙或移動過程中超過了青蛙所允許的最大移動距離,那么就隨機生成一個新的青蛙直接替代原來的Fw。重復數次以上局部位置更新操作,并將所有模因組內的青蛙重新混合排序和劃分模因組,再執行下一輪的數次局部位置更新操作,直到滿足預先設定的收斂條件或者達到混合最大迭代次數為止。
為了加快混合蛙跳優化算法的收斂速度和減少其局部位置更新操作的次數,本文在文獻[14-15]的基礎上,對其稍作些修改:對其局部位置更新操作,引入加速因子。僅需執行一次局部位置更新操作,取消多次重復執行該操作。修改后的混合蛙跳算法的局部位置更新操作為
(3)
式中c——加速因子
若更新后得到的青蛙優于原來的青蛙,則可替代原模因組內的青蛙Fw;否則,用Fg代替Fb,執行局部位置更新操作
(4)
如果式(4)等操作仍然不能獲得更好適應值的青蛙或移動過程中超過了青蛙所允許的最大移動距離Dmax,那就隨機生成一個新的青蛙直接替代原來的Fw。
修改后混合蛙跳優化算法的具體實現過程為:
(1)初始化相關參數,在所求問題的定義域內隨機產生N只青蛙,構成一個初始種群,并置模因組數為m,模因組內的青蛙個數為n,使其滿足N=m×n;置混合最大迭代次數為G。
(2)計算每只青蛙的適應值,并按照其適應值的大小降序排列、選出該種群中具有最優適應值的Fg和劃分模因組。
(3)選出每個模因組的Fb,依據式(3)和式(4),執行局部位置更新操作,更新每個模因組的Fw。
(4)判斷混合迭代次數是否達到G或者是否符合預先設定的收斂條件,如果不滿足,則返回步驟(2)繼續執行;如果滿足,則結束算法,輸出Fg,即所求問題的解。
1.2.2改進LM算法
相機模型參數的非線性優化,一般可歸納為非線性最小二乘問題。LM算法是解決該類問題較為有效的方法[16]。但是,LM算法需要求取優化參數函數的雅可比矩陣。而相機模型的優化參數函數往往都很復雜,很難通過偏導方法求取其雅可比矩陣。為此,本文采用文獻[17]提出的改進LM算法,把原LM算法采取求偏導方式來獲取優化參數函數的雅可比矩陣替換為通過求差商方式來獲取。
一般非線性最小二乘問題,都可構造目標優化函數
(5)
其中f(X)=[f1(X)f2(X) …fm(X)]T
fi(X)=fi(x1,x2,…,xn)
X=(x1,x2,…,xn)T
式中X——需要優化的參數向量
xi——需要優化的參數(i=1,2,…,m)
改進LM算法的具體步驟可描述為:
(1)給出需要優化的參數向量的初值X(1),初始化阻尼系數c、放大系數β(一般憑經驗可取c=0.01,β=10)、允許誤差ε,并計算出F(X(1))。
(2)令c?c/β,并且計算出需要優化的參數向量f(k)及其雅可比矩陣Ak。
f(k)=[f1(X(k))f2(X(k))…fm(X(k))]T
(6)
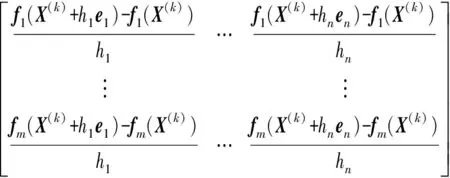
(7)
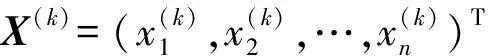
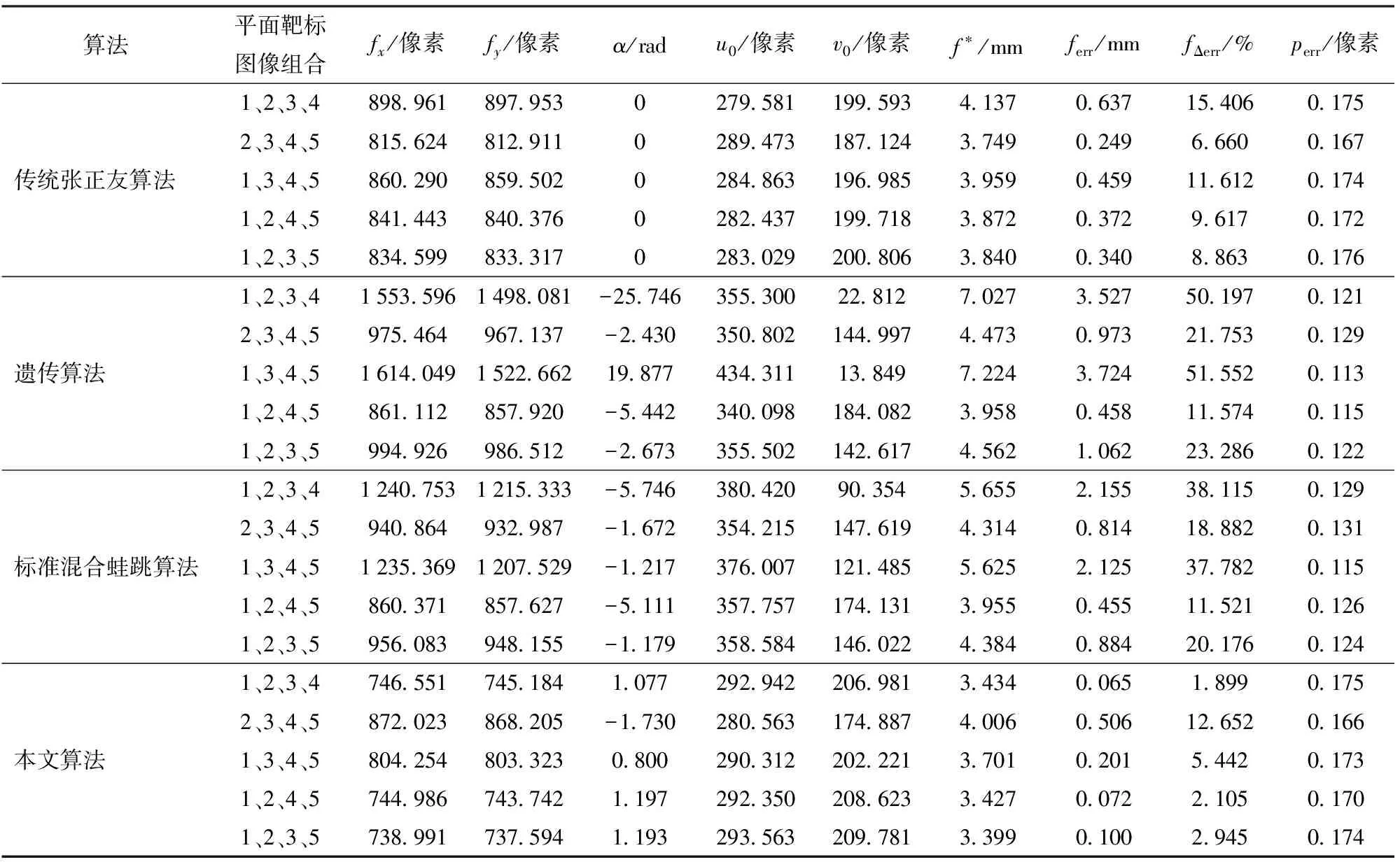
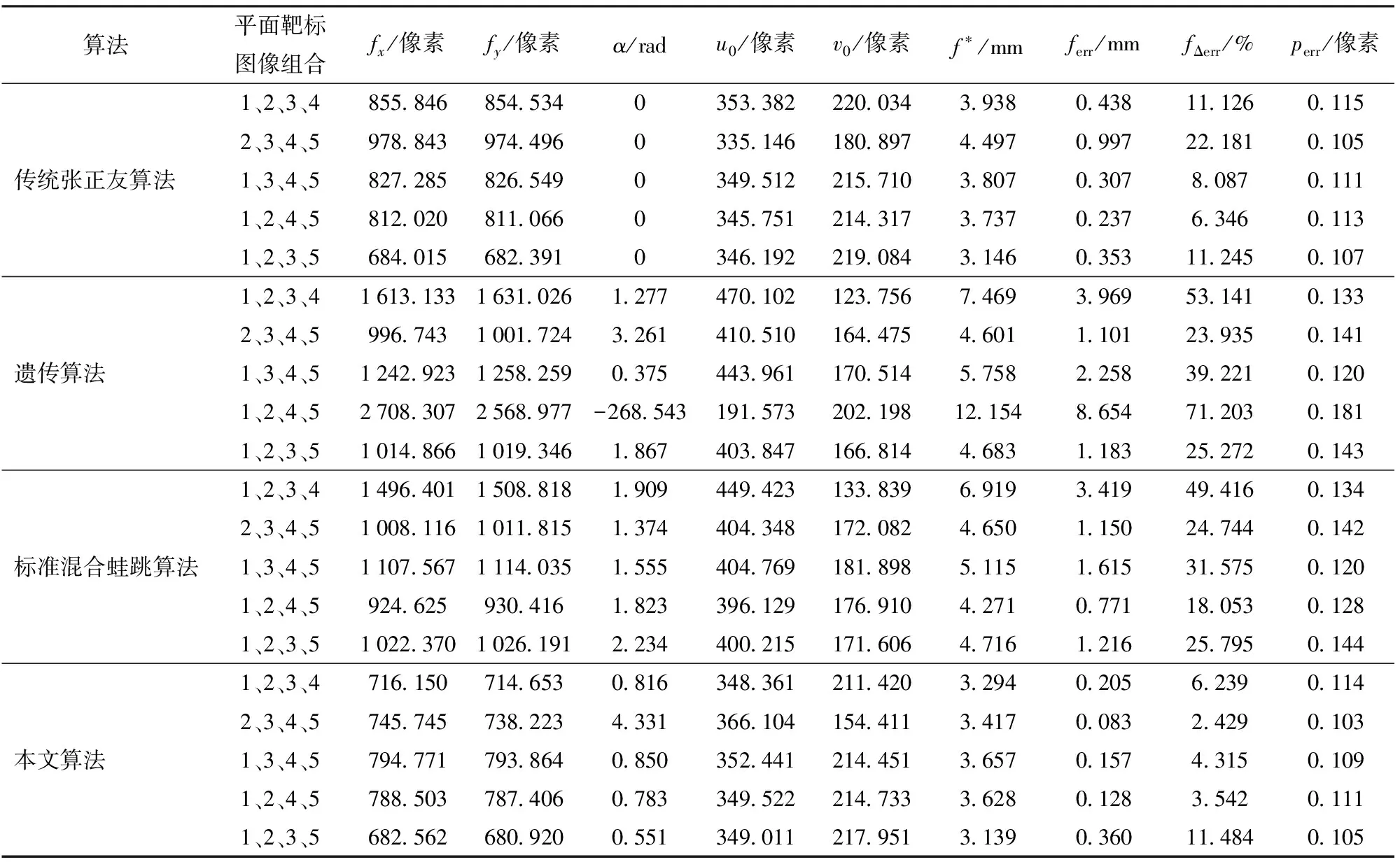
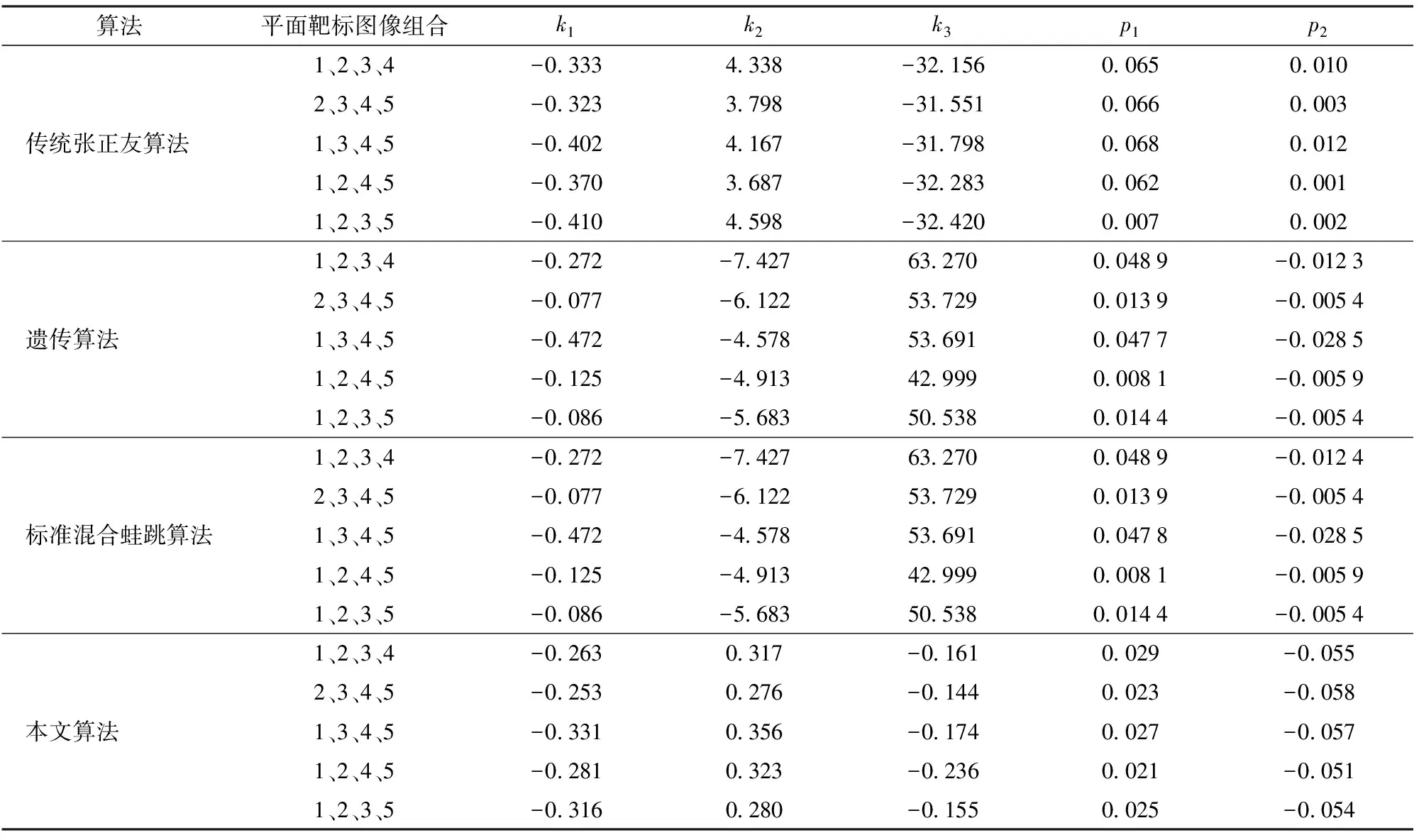
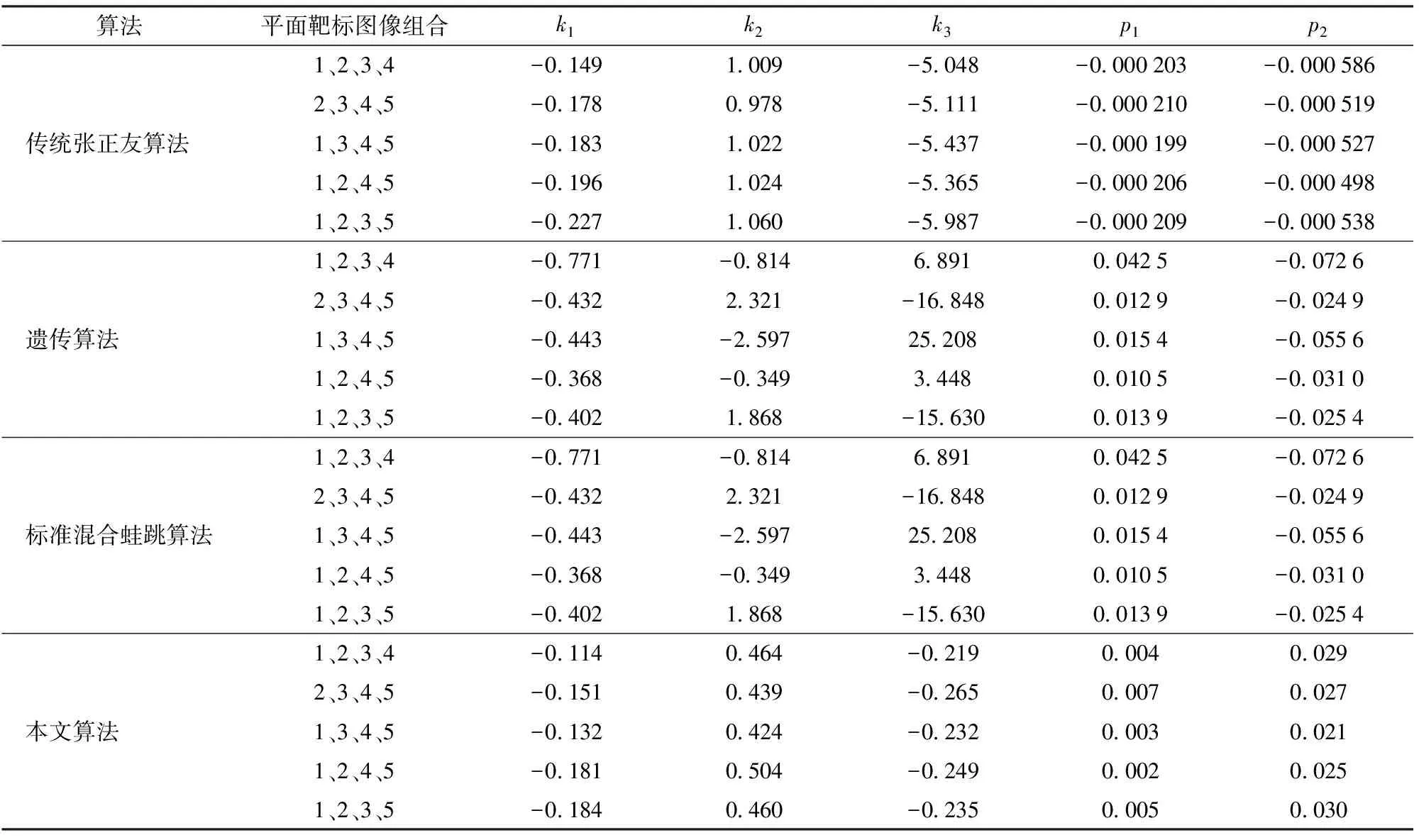
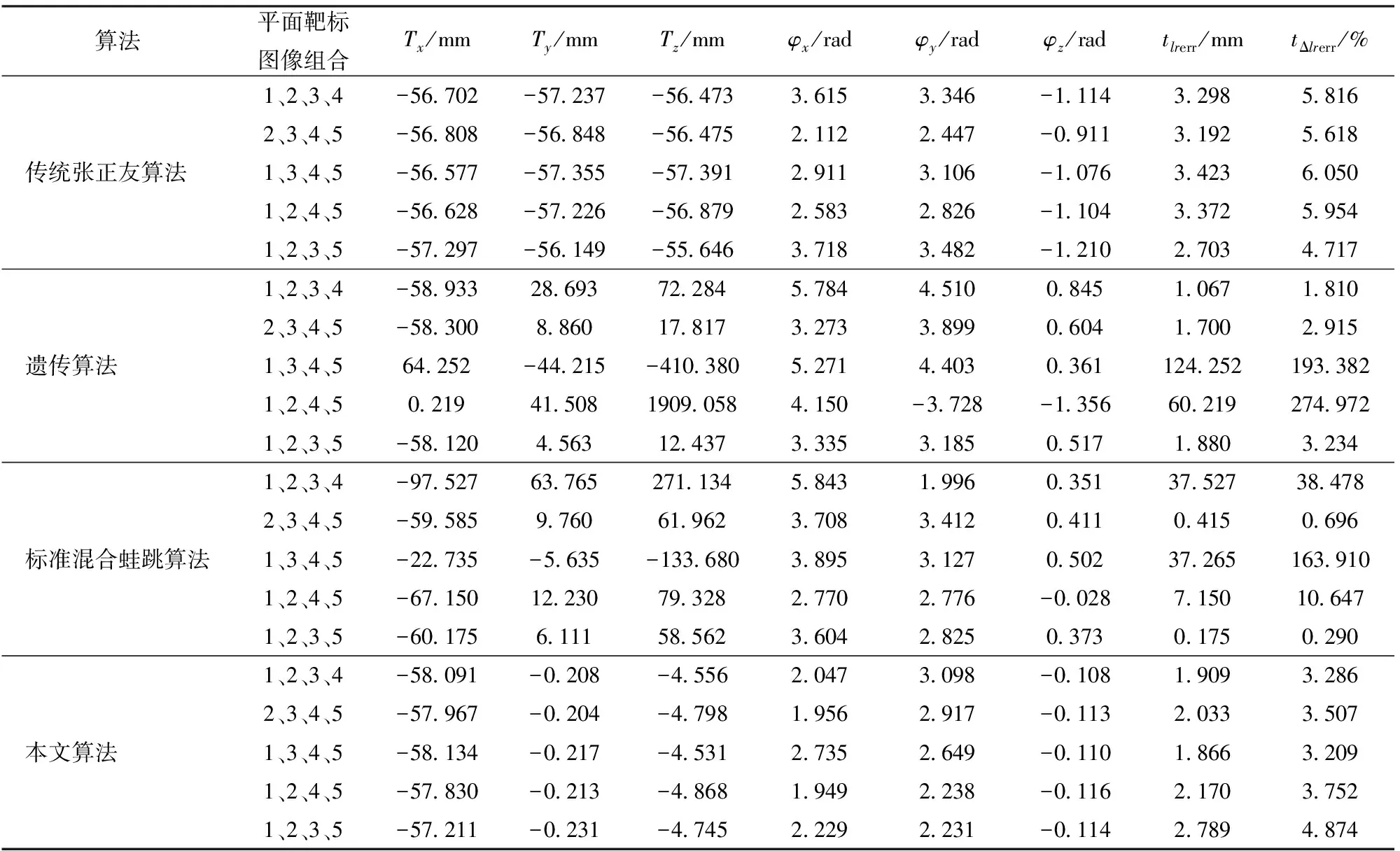
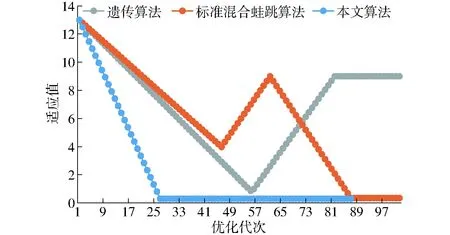
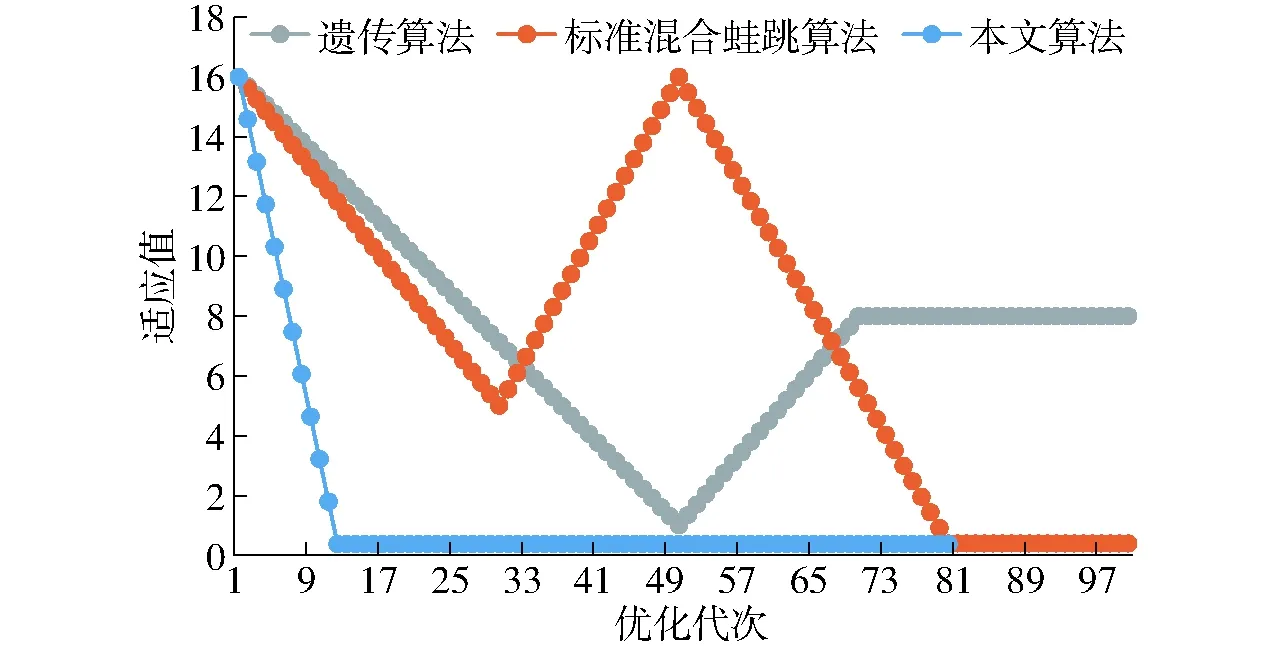
(4)計算F(X(k+1)),如果F(X(k+1)) 1.2.3結合混合蛙跳和改進LM算法的相機標定 參照張正友相機標定原理,結合混合蛙跳優化算法和改進LM算法的各自優點,把相機標定過程劃分為以下兩步:第1步,以混合蛙跳算法為工具,求出相機模型參數的初始值。第2步,以改進LM算法對第1步求出的相機模型參數的初始值,進一步非線性優化求精,最終求得標定精度較高的相機模型參數。 一般相機模型需要標定的參數包括:內部參數(fx,fy,α,u0,v0)、外部參數(R,T)和畸變參數(k1,k2,k3,p1,p2)。而外部參數求取公式為 (8) 式中K——相機模型的內參數矩陣 H——單應性矩陣 h1、h2、h3——H的第1、2、3列向量 s——比例系數 r1、r2、r3——R的第1、2、3列向量 改進LM算法對相機參數非線性優化目標函數定義為平面靶標圖像的二維重投影誤差 (9) 式中Iij——第i幅平面靶標圖像上第j個特征點在圖像像素坐標系下的坐標 Pij——第i幅平面靶標圖像上第j個特征點的三維世界坐標 L——平面靶標圖像數 M——單幅平面靶標圖像特征點數 為了減少混合蛙跳算法的搜索維數,本文僅利用混合蛙跳算法來尋求相機模型的內部參數和畸變參數,而每一幅平面靶標圖像的相機模型外部參數由式(8)來求取。為此,依據混合蛙跳算法的原理,可以把每一只青蛙個體表示為 (10) 式中Fk——第k只青蛙個體 顯然,又可把混合蛙跳算法的每個模因組內具有最好適應值和最差適應值以及整個種群中具有最優適應值的青蛙個體表示為 (11) (12) (13) 并依據二維圖像特征點與三維空間點之間的二維重投影誤差和混合蛙跳算法的特點,求取青蛙個體適應值函數 (14) 基于改進混合蛙跳和LM算法的相機標定詳細步驟為: (1)提取所有平面靶標圖像特征點圖像像素坐標系下的二維坐標,同時根據平面靶標圖像特征點的二維坐標以及其三維世界坐標,利用最小二乘法直接求取每幅平面靶標圖像的單應性矩陣H。 (15) 式中 rand()——0~1之間的隨機函數 Wk、Hk——平面靶標圖像的寬度和高度 (4)選出每個模因組Fb,依據式(3)和式(4),執行局部位置更新操作,更新每個模因組Fw。 (5)判斷混合迭代次數是否達到G或者是否達到預先設定最小適應值η,如不滿足,則返回步驟(3)繼續執行;如滿足,則轉到步驟(6)。 1.2.4雙目相機立體標定 由于采摘機器人采用雙目相機視覺系統,所以不僅需知左、右相機模型的內、外參數,還需知左、右相機之間的對應關系(即左、右相機之間的旋轉矩陣和三維平移向量)。 其具體的求解過程為先按照前面介紹的相機標定方法,分別單獨求出左、右相機模型的參數,然后依據左、右相機之間的對應關系,求出左、右相機之間的旋轉矩陣Rlr和三維平移向量Tlr[18-20]。 假設三維空間中的任意一點P,在世界坐標系、左相機坐標系以及右相機坐標系下的非齊次坐標分別為XW、XCl、XCr,則有 (16) 式中Rl、Tl——左相機模型的外部參數旋轉矩陣和三維平移向量 Rr、Tr——右相機模型的外部參數旋轉矩陣和三維平移向量 整理式(16),可得 XCl=RlrXCr+Tlr (17) 根據采摘機器人視覺定位精度的要求(視覺定位位置絕對誤差0.1~1 mm,相對誤差1%~10%)以及雙目視覺系統的標定原理,本文設計了由1個三角架、2個出廠參數相同的廣角相機(出廠焦距參數f為3.5 mm,像元橫向物理尺寸dx為4.65 μm,像元縱向物理尺寸dy為4.65 μm,兩個相機主光心之間距離即雙目相機之間距離為60 mm)和平面靶標(平面靶標方格的邊長為25 mm)組成的采摘機器人雙目相機標定試驗平臺(圖2)。 圖2 雙目相機標定試驗平臺Fig.2 Test platform of binocular camera calibration 運用OpenCV2.3.1、VS2008和OpenGL編程實現了采摘機器人雙目視覺標定系統,見圖3。該標定系統包括OpenCV自帶的傳統張正友相機標定方法、基于遺傳算法的相機標定方法(設置交叉概率p為0.8,變異概率q為0.2,優化閾值t為0.5,種群大小N為50,最大迭代次數G為100)、基于標準混合蛙跳算法的相機標定方法(設置加速因子c為0.5,優化閾值t為0.5,種群大小N為50,模因組大小m為5,模因組組內青蛙個數n為10,最大迭代次數G為100)和基于改進混合蛙跳和LM算法的相機標定方法(即本文相機標定方法,設置加速因子c為0.5,優化閾值t為0.5,種群大小N為50,模因組大小m為5,模因組組內青蛙個數n為10,最大迭代次數G為100)。按照圖4所示的試驗流程,在室外進行相機標定試驗。 圖3 采摘機器人雙目視覺標定系統Fig.3 Binocular camera calibration system of harvesting robot 圖4 相機標定試驗步驟流程Fig.4 Test procedures of camera calibration 為了評價以上相機標定方法的性能,本文根據誤差理論,設計了以下評價指標。 相機焦距絕對誤差 ferr=|f*-f| (18) 其中 f*=(fxdx+fydy)/2 式中f*——由相機內部參數fx、fy以及相機像元尺寸參數dx、dy計算出的相機焦距 相機焦距相對誤差 fΔerr=|(f*-f)/f*|×100% (19) 平面靶標圖像特征點平均像素誤差 (20) 雙目相機間距絕對誤差 (21) tlr——實際的雙目相機間距(本文中為60 mm) 雙目相機間距相對誤差 (22) 同時,考慮到隨著平面靶標圖像數量的增加,在同等標定環境下,平面靶標圖像的特征點的提取誤差和畸變誤差也不可避免地帶入相機標定過程,從而影響相機標定參數的精度和穩定性。為此,本文不選擇通過采集大量平面靶標圖像進行相機標定試驗,而是根據張正友相機標定方法至少所需平面靶標圖像數量的要求:只需4幅不同的平面靶標圖像,即可完成相機內、外參數標定,左、右相機分別采集5幅不同的平面靶標圖像,具體見圖5、6。 圖5 左相機采集到的5幅平面靶標圖像Fig.5 Fine capturing planar target images of left camera 圖6 右相機采集到的5幅平面靶標圖像Fig.6 Fine capturing planar target images of right camera 然后,利用左、右各5幅平面靶標圖像中的4幅圖像的不同組合進行相機標定,并依據相機焦距絕對誤差、相機焦距相對誤差、平面靶標圖像特征點的平均像素誤差、雙目相機間距的絕對誤差以及雙目相機間距的相對誤差的性能評價指標,對以上相機標定方法進行性能評價。具體相機標定參數結果和性能評價結果,見表1~5。 為了比較基于遺傳算法的相機標定方法、基于標準混合蛙跳算法的相機標定方法和本文相機標定方法的收斂性,分別統計了100次標定優化過程中適應值的變化趨勢,結果見圖7、8。 對比表1、2,可知在以上5組不同組合相機標定試驗中,傳統張正友相機標定方法獲得的左相機焦距絕對誤差ferr為0.340~0.637 mm,焦距相對誤差fΔerr為6.660%~15.406%,平面靶標圖像特征點的平均像素誤差perr為0.167~0.176像素,右相機焦距絕對誤差ferr變化范圍為0.237~0.997 mm,焦距相對誤差fΔerr變化范圍為6.346%~22.181%,平面靶標圖像特征點的平均像素誤差perr為0.105~0.115像素;基于遺傳算法的相機標定方法獲得的左相機焦距絕對誤差ferr為0.458~3.724 mm,焦距相對誤差fΔerr為11.574%~51.552%,平面靶標圖像特征點的平均像素誤差perr為0.113~0.129像素,右相機焦距絕對誤差ferr為1.101~8.654 mm,焦距相對誤差fΔerr為23.935%~71.203%,平面靶標圖像特征點的平均像素誤差perr為0.120~0.181像素;基于標準混合蛙跳算法的相機標定方法獲得的左相機焦距絕對誤差ferr為0.455~2.155 mm,焦距相對誤差fΔerr為11.521%~38.115%,平面靶標圖像特征點的平均像素誤差perr為0.115~0.131像素,右相機焦距絕對誤差ferr為0.771~3.419 mm,焦距相對誤差fΔerr為18.053%~49.416%,平面靶標圖像特征點的平均像素誤差perr為0.120~0.144像素;本文相機標定方法獲得的左相機焦距絕對誤差ferr為0.065~0.506 mm,焦距相對誤差fΔerr為1.899%~12.652%,平面靶標圖像特征點的平均像素誤差perr為0.166~0.175像素,右相機焦距絕對誤差ferr為0.083~0.360 mm,焦距相對誤差fΔerr為2.429%~11.484%,平面靶標圖像特征點的平均像素誤差perr為0.103~0.114像素。 對比表3、4可知,在以上5組不同組合的相機標定試驗中,傳統張正友相機標定方法獲得的左相機畸變參數k1為-0.410~-0.323,k2為3.687~4.598,k3為-32.420~-31.551,p1為0.007~0.068,p2為0.001~0.012,右相機畸變參數k1為-0.227~-0.149,k2為0.978~1.060,k3為-5.987~-5.048,p1為-0.000 210~-0.000 199,p2為-0.000 586~-0.000 498;基于遺傳算法的相機標定方法獲得的左相機畸變參數k1為-0.472~-0.077,k2為-7.427~-4.578,k3為42.999~63.270,p1為0.008 1~0.048 9,p2為-0.028 5~-0.005 4,右相機畸變參數k1為-0.771~-0.368,k2為-2.597~2.321,k3為-16.848~25.208,p1為0.010 5~0.042 5,p2變化范圍為-0.072 6~-0.024 9;基于標準混合蛙跳算法的相機標定方法獲得的左相機畸變參數k1為-0.472~-0.077,k2為-7.427~-4.578,k3為42.999~63.270,p1為0.008 1~0.048 9,p2為-0.028 5~-0.005 4,右相機畸變參數k1為-0.771~-0.368,k2為-2.597~2.321,k3為-16.848~25.208,p1為0.010 5~0.042 5,p2為-0.072 6~-0.024 9;本文相機標定方法獲得的左相機畸變參數k1為-0.331~-0.253,k2為0.276~0.356,k3為-0.236~-0.144,p1為0.021~0.029,p2為-0.058~-0.051,右相機畸變參數k1為-0.184~-0.114,k2為0.424~0.504,k3為-0.265~-0.219,p1為0.002~0.007,p2為0.021~0.030。 表1 不同相機標定方法獲得的左相機標定內參結果及性能評價指標Tab.1 Left camera calibration results and evaluation index with different camera calibration methods 表2 不同相機標定方法獲得的右相機內參標定結果及性能評價指標Tab.2 Right camera calibration results and evaluation index with different camera calibration methods 表3 不同相機標定方法獲得的左相機標定畸變結果Tab.3 Left camera calibration distortion results with different camera calibration methods 表4 不同相機標定方法獲得的右相機標定畸變結果Tab.4 Right camera calibration distortion results with different camera calibration methods 表5 不同相機標定方法獲得的雙目相機標定結果及性能評價指標Tab.5 Binocular camera calibration results and evaluation index with different camera calibration methods 圖7 左相機標定過程中的適應值變化曲線Fig.7 Variation curves of adaptive value in calibration of left camera 圖8 右相機標定過程中的適應值變化曲線Fig.8 Variation curves of adaptive value in calibration of right camera 在表5中,Tx為雙目相機之間平移向量的X方向分量,Ty為雙目相機之間平移向量的Y方向分量,Tz為雙目相機之間平移向量的Z方向分量;φx為雙目相機之間旋轉角向量的X方向分量,φy為雙目相機之間旋轉角向量的Y方向分量,φz為雙目相機之間旋轉角向量的Z方向分量。 由表5可知,傳統張正友相機標定方法獲得的雙目相機之間平移向量的分量Tx、Ty、Tz分別為-57.297~-56.577 mm、-57.355~-56.149 mm、-57.391~-55.646 mm,雙目相機之間旋轉角向量的分量φx、φy、φz分別為2.112~3.718 rad、2.447~3.482 rad、-1.210~-0.911 rad,雙目相機間距絕對誤差tlrerr為2.703~3.423 mm,相對誤差tΔlrerr為4.717%~6.050%;基于遺傳算法的相機標定方法獲得的雙目相機之間平移向量的分量Tx、Ty、Tz分別為-58.933~64.252 mm、-44.215~41.508 mm、-410.380~1 909.058 mm,雙目相機之間旋轉角向量的分量φx、φy、φz分別為3.273~5.784 rad、-3.728~4.510 rad、-1.356~0.845 rad,雙目相機間距絕對誤差tlrerr為1.067~124.252 mm,相對誤差tΔlrerr為1.810%~274.972%;基于標準混合蛙跳算法的相機標定方法獲得的雙目相機之間平移向量的分量Tx、Ty、Tz分別為-97.527~-22.735 mm、-5.635~63.765 mm、-133.680~271.134 mm,雙目相機之間旋轉角向量的分量φx、φy、φz分別為2.770~5.843 rad、1.996~3.412 rad、-0.028~0.502 rad,雙目相機間距絕對誤差tlrerr為0.175~37.527 mm,相對誤差tΔlrerr變化范圍為0.290%~163.910%;本文相機標定方法獲得的雙目相機之間平移向量的分量Tx、Ty、Tz分別為-58.134~-57.211 mm、-0.231~-0.204 mm、-4.868~-4.531 mm,雙目相機之間旋轉角向量的分量φx、φy、φz分別為1.949~2.735 rad、2.231~3.098 rad、-0.116~-0.108 rad,雙目相機間距絕對誤差tlrerr為1.866~2.789 mm,相對誤差tΔlrerr為3.209%~4.874%。 由此可見,對于左、右相機焦距的絕對誤差和相對誤差變化,本文相機標定方法最小,傳統張正友相機標定方法次之,基于遺傳算法的相機標定方法和基于標準混合蛙跳算法的相機標定方法變化較大;對于平面靶標圖像特征點的平均像素誤差變化,雖然基于遺傳算法的相機標定方法和基于標準混合蛙跳算法的相機標定方法稍微小些,但跟傳統張正友相機標定方法以及本文相機標定方法的差異不大,都在1像素之內。而相機畸變參數,按照文獻[3],認為合適的變化范圍為-1~1,但以上4種相機標定方法,除了本文相機標定方法所獲得的所有畸變參數均符合-1~1的變化范圍外,其余的相機標定方法所獲得的畸變參數k2、k3、p1、p2均不在此變化范圍之內,且變化也相對較大。而雙目相機間距絕對誤差和相對誤差,基于遺傳算法的相機標定方法最大,分別達到124.252 mm和274.972%;基于標準混合蛙跳算法的相機標定方法也相對較大,分別達到37.527 mm和163.910%;傳統張正友相機標定方法相對較小,而本文相機標定方法最小。 同時,比較圖7、8,可以看出本文相機標定方法的左、右相機標定,適應值隨著優化次數增加而下降,分別經過約26次和12次優化后,收斂到一個穩定的適應值;基于遺傳算法的相機標定方法的左、右相機標定,適應值先下降后上升,最后分別經過約86次和71次優化后,才收斂到一個穩定的適應值;基于標準混合蛙跳算法的相機標定方法的左、右相機標定,適應值先下降再上升后又下降,最后分別經過約86次和81次優化后,才收斂到一個穩定的適應值。顯然可見,本文相機標定方法的收斂速度和穩定性,均優于基于遺傳算法的相機標定方法和基于標準混合蛙跳算法的相機標定方法。 以上分析表明,本文相機標定方法所獲得的左、右相機內參數fx、fy、α、u0、v0,畸變參數k1、k2、k3、p1、p2和雙目相機參數Tx、Ty、Tz、φx、φy、φz均比以上其他3種相機標定方法更為準確可靠。這是因為傳統張正友相機標定方法是通過對單應性矩陣奇異值分解來求取相機內參初值,然后利用LM算法對該相機內參數進一步求精。但矩陣奇異值分解存在數值不穩定,并且LM算法優化結果的精度取決于參數初始值,這樣將影響求取的相機內參數的最終精度。而基于遺傳算法的相機標定方法、基于標準混合蛙跳算法的相機標定方法和本文相機標定方法,先采用仿生智能優化策略直接求取相機內參數初值,避免了對單應性矩陣奇異值分解所造成的相機內參數初值不準確,再利用改進LM算法進一步優化相機內參數,避免了原LM算法優化過程必須求取優化參數的雅可比矩陣所導致求取參數精度的不穩定。但這些仿生智能優化算法本質是基于概率統計規律的隨機搜索,隨機性很強,面對求取相機內參數這樣多元參數非線性優化問題,極容易陷入局部極值,從而造成相機內參數精度不穩定以及優化收斂過程過于緩慢。而本文相機標定方法對標準混合蛙跳算法的局部位置更新操作進行了改進,協調其全局搜索和局部開采的能力,提高了其收斂速度,避免了求取相機內參數初值陷入局部極值的問題,所以本文相機標定方法求取相機內參數比基于遺傳算法的相機標定方法以及基于標準混合蛙跳算法的相機標定方法更為準確可靠。此外,因為標準混合蛙跳算法比遺傳算法的全局搜索能力強,所以它求取的相機內參結果比基于遺傳算法的結果理想。同時,由于相機畸變參數和雙目相機參數,是在相機內參數基礎上求取的,所以相機內參數的準確性將直接影響相機畸變參數和雙目相機參數的準確性。由于本文相機標定方法所求取的相機內參數比其他3種相機標定方法結果均更為準確,因此,本文相機標定方法所求取的相機畸變參數和雙目相機參數也相對更為準確可靠。 根據對采摘機器人相機標定精度的要求,針對傳統張正友相機標定方法存在標定結果不穩定、容易陷入局部極值等缺點,提出了一種基于改進混合蛙跳和LM算法的相機標定方法。該相機標定方法只需4幅不同平面靶標圖像即可完成相機標定,并且相機焦距的絕對誤差、相對誤差,平面靶標圖像特征點的平均像素誤差,雙目相機間距絕對誤差、相對誤差等相機標定性能評價指標都符合采摘機器人相機標定精度的要求。標定所獲得的左、右相機內參數、畸變參數以及雙目相機之間的參數,均優于傳統張正友相機標定、基于遺傳算法的相機標定和基于標準混合蛙跳算法的相機標定等方法。同時,在相機標定優化過程中,只需很少次優化,即可收斂到穩定的適應值,具有較高的收斂速度和穩定性,能夠滿足采摘機器人雙目視覺定位系統的要求,是一種精度高且簡便的相機標定方法。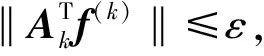
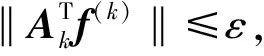
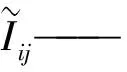
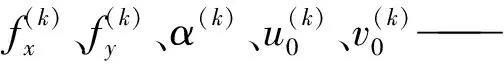
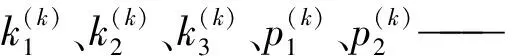
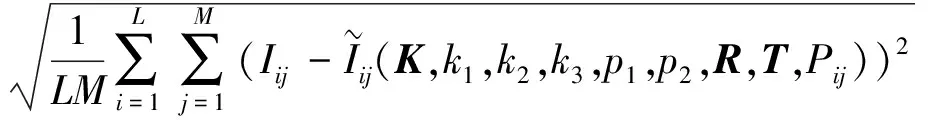
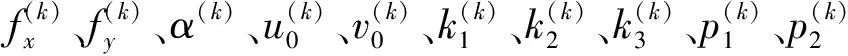
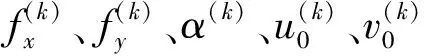
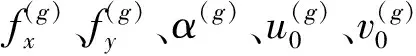
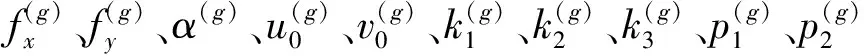
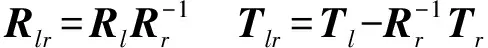
2 試驗與結果分析


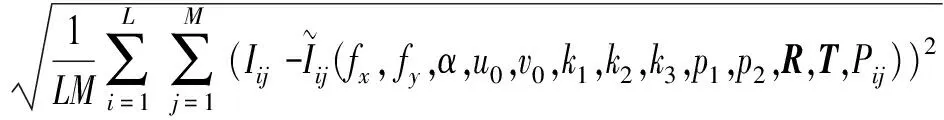



3 結束語

