免疫遺傳神經網絡算法的紗線原料性能反演

查劉根 謝春萍

(江南大學，江蘇無錫 ，214122)

紗線生產加工過程中，其質量的優劣不僅取決于生產加工工藝、工人的技術水平以及機械設備的性能，更是與原棉質量的優劣及不同批次原棉的搭配使用情況存在著密不可分的聯系[1-3]。紗線質量預測問題的一個重要的研究方向是科學地分析紗線產品質量與原棉性能之間存在的必然聯系，建立最為逼近的數學模型，最大程度地利用各批原棉自身的優良性能，從而起到穩定生產，節約成本的作用[4-5]。

紗線質量預測模型是一種非線性優化模型，可通過非線性函數來表達，其反演模型解決的也是一種非線性最優化問題，可用于指導配棉[6]。正演模型中輸出的紗線質量參數是確定的，而其中一個或多個輸入的原棉性能參數可通過構造的反演模型獲得多組不同的組合，然后綜合考慮生產成本和產品要求選出最優的參數組合，從而可設計出更加合理的配棉方案。近年來，國內外廣泛使用BP神經網絡和遺傳算法等全局優化算法處理反演問題。文獻[7]提出了一種修改的非線性共梯度算法，該方法主要利用IRLS(Iterative Reweighted Least Square )算法的加權思想來改變搜索方向從而增加穩定性。文獻[8]采用直接逼近法來反演棉花模型所需的初始數據及參數，將遙感信息和棉花模型相結合，建立遙感-棉花的反演模型，試驗驗證了該模型是可行的。針對傳統參數反演算法存在收斂性和穩定性不理想、反演精度較低、計算速度較緩慢，以及標準遺傳算法存在的早熟收斂等問題，本文利用免疫遺傳算法優化BP神經網絡的權值和閾值來建立遺傳神經網絡正演模型，根據紗線強力值來反演原棉性能的輸入參數，研究結果可為紡織企業的配棉工作提供可靠的理論依據。

1 模型簡介與參數選擇

本文選取紗線質量預測模型作為研究對象，主要考慮到以下幾個方面的因素：首先,它是一個經過大量試驗數據驗證并在實際中得到應用的一個模型；其次, 模型是動態和非線性的，參數之間具有較強的相互作用；最后，模型的結構相對比較簡單，參數之間的關系容易把握。

紗線的生產加工，其產品的質量與原料的性能及工藝參數的設定緊密相關。理論上講，預測的紗線質量參數不同，選取的原料性能參數和生產工藝參數均不同。但是，反演參數設定過多，就會降低優化的準確性，延長優化時間，所以，本文的反演參數的選擇主要考慮變化范圍較大的，模型比較敏感的若干原料性能參數[9]。當輸出的紗線質量參數確定后，通過反演模型去尋找滿足實際生產需要的原料性能參數組合，再綜合考慮原料成本與產品質量要求等條件篩選出最佳組合參數，從而設計出更加合理的配棉方案。

2 反演模型的數學表述

因為在紗線原料性能參數的反演問題中，誤差泛函是復雜的多峰函數，所以這里需要構建的是一種全局尋優反演模型。將參數反演抽象為數學模型，描述如下。

(1)設Y是紗線的某一重要性能參數，{p1,p2,…,pn}是此紗線的部分原料性能參數，Y={p1,p2,…,pn}，即Y的值可由集合{p1,p2,…,pn}中的參數預測得出。

(2)假設pi和pj是兩個重要的原棉參數，現需要為某一配棉方案確定更多的組合以供選擇，也就要反演獲得更多的參數pi和pj。通過構建神經網絡，以一組{p1,p2,…,pn}為輸入參數，以參數Y作為網絡的輸出，然后將通過訓練得到的網絡封裝成一個函數，f(p1,p2,…,pn)，即對任意的{p1,p2,…pi…pj…,pn}集合，都可以由函數f計算求得Y。

(3)構造免疫遺傳算法，將pi和pj編碼成染色體。正演模型的誤差可表示為：

E(p1,p2,…,pn)=f(p1,p2,…,pn)-Y真實值

(1)

則反演模型的目標函數(適應度函數)可表示為：

F(p)= min{abs[E(p1,p2,…pi…pj…,pn)]}

(2)

從而得到反演參數pi和pj。

3 反演算法設計

3.1 反演的基本步驟

反演算法的流程圖如圖1所示。

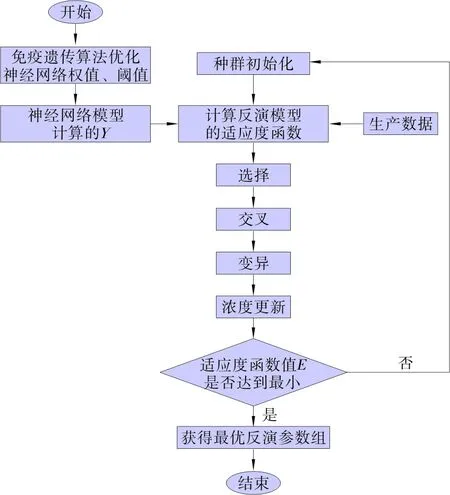
圖1 反演算法流程圖

(1)基于已知純棉紗線纖維樣本的馬克隆值、上半部平均長度、整齊度、短纖維指數和單纖維強度等條件，結合免疫遺傳算法和神經網絡算法建立針對初始紗線強力值的預測模型。

(2)根據建立的初始紗線強力值預測模型得到預測結果，可以得到實際數據與計算數據的均方根誤差，若滿足精度要求則迭代結束，否則繼續迭代直至精度符合要求。

(3)基于當前正演模型，通過免疫遺傳算法構造其反演模型，用來反演原料性能參數。

(4)以紗線強力值實測數據與預測數據的差作為適應度函數的值，通過迭代尋優，得到最佳性能參數組合。

(5)根據正演模型計算紗線強力值預測數據，從而得到目標函數值，根據目標函數值的精確度得到最合適的原料性能參數。

3.2 免疫遺傳算法的BP神經網絡設計

3.2.1 BP神經網絡建模

本文構造的單紗強力預測模型所使用的數據來源于山東某棉紡織廠的原棉物理指標及細紗質量指標，為提高預測結果的準確性和計算的穩定性，數據在使用之前使用log函數進行了統一的歸一化處理。網絡以馬克隆值、上半部平均長度、整齊度、短纖維指數和強度作為輸入，以紗線強力值為輸出，即輸入層有m=5個神經元，輸出層有n=1個神經元，隱含層單元數可由經驗公式(3)[10]得到s=4，最后，得到的三層BP神經網絡的拓撲結構如圖2所示。

s=

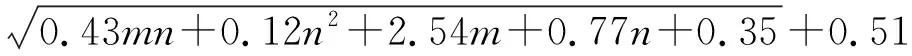
(3)

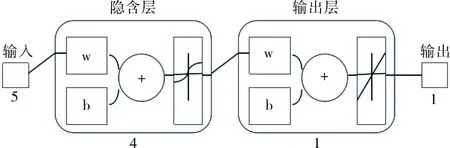
圖2 3層網絡結構

3.2.2 網絡權值和閾值的優化設計

(1)編碼：將待尋優變量即神經網絡的連接權值和閾值作為抗體進行編碼，考慮到單獨的二進制編碼的復雜性以及計算量大的缺點，本文主要采用實數編碼，在基于濃度的群體更新時再轉換成二進制進行操作，可有效提高算法的收斂速度。

(2)初始群體的產生：隨機化生成M個抗體組成初始種群。設輸入單元數為m，隱層單元數為n，輸出單元數為l，則連接權值共有m×n+n×l個，閾值共有n+l個，抗體長度為L=m×n+n×l+n+l。

(3)適應度函數的設計：對于給定的訓練數據與實際數據，將實際數據與預測數據的平均絕對誤差E定義為BP神經網絡的目標函數F(x)=minE，而免疫遺傳算法解決的一般是目標最大化問題，故最終的適應度函數設定為Fitness(x)=1/F(x)。

(4)遺傳操作。

選擇：采用適應度比例的方法選擇子代抗體，設M為抗體數量，fj是第j個抗體的適應度值，那么該抗體被選擇的概率為pj，適應度比例法很好地保留下了高適應度的父代抗體，保證優良基因逐代遺傳，有效地維持了算法的全局搜索能力。

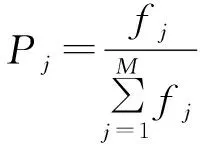
(4)

交叉：本文采用算數交叉法，通過設定一個參數α和線性重組可以產生任意兩個位于兩個父代抗體間的子代抗體。

變異：變異操作能恢復抗體失去的或未開發的有效信息，維持群體的多樣性，本文采用單重均勻變異法。

(5)基于濃度的群體更新：如果只是通過簡單的遺傳選擇篩選出大量的高適應度父代抗體，而不施加控制，那么這些個體的濃度就會越來越高，收斂后期群體的多樣性便會急劇降低，最終算法陷入局部極值。所以，就需要找到一個更好的方法，既能保留住高適應的個體，還可以確保在新產生的抗體群里，適應度值較低但可能包含優良基因的個體也有被挑選出來的機會，這就是基于濃度機制的群體更新，該操作能夠維持每代抗體群的多樣性。

在這里先給出信息熵、相似度和抗體濃度的概念和計算公式。

信息熵:免疫系統中，一個抗體所包含的信息量可由香農的平均信息熵H(M)來表述。設某抗體包含S種不同的符號，某一符號位于t號基因座的概率pst可由式(5)計算得出，即：

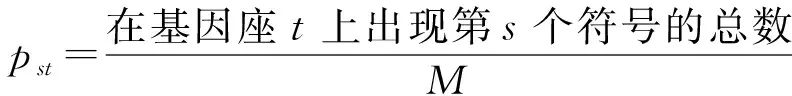
(5)

則Ht(M)為第t基因的信息熵，定義為：

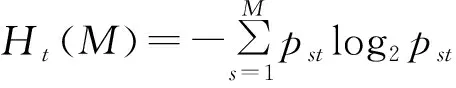
(6)

整個群體的平均信息熵為

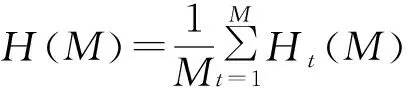
(7)

相似度：抗體a和抗體c相似的程度稱之為它們的相似度。

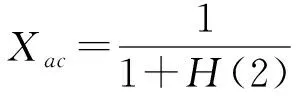
(8)

H(2)可由式(7)計算得出，是兩個抗體的平均信息熵。還可以定義群體的相似度X(M)：

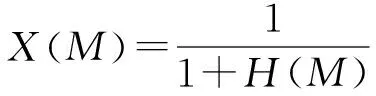
(9)

X(M)的大小反映了整個群體的相似程度，X(M)∈(0，1)，X(M)越大，群體相似度越高，當X(M)=1時，表示所有抗體完全相同的。

抗體濃度：抗體濃度是指某個抗體和與其相似的個體在種群中的比率，可由公式(10)[11]求得，其中，σ為相似度常數，一般取0.9～1。

(10)

伴隨著抗體群的不斷更新，部分抗體的相似度必定會逐漸增大，為了有效地保持群體的多樣性，為其相似度設定一個閾值(設為X0，X0與抗體群規模的大小呈正比)，當群體發展到其相似度大于該閾值時，就將隨機增殖Z個新抗體，抗體總數擴大為M+Z。

在單一適應度評價方法之上，加入抗體濃度進行調整，提出聚合適應度的概念，作為最后篩選個體的評價指標，其表達式如式(11)[12]所示，其中，對于本文的最大優化問題，β應為負數，取β= -0.6。

聚合適應度=適應度×exp(β×Ca)

(11)

采用聚合適應度比例的方法更新下一代群體，某抗體被保留下來的幾率與其聚合適應度呈正相關，最終篩選出M個抗體作為下一代的種群。這種做法的優點在于，一方面抗體的濃度不變時，聚合適應度的大小與適應度的值呈正相關，能夠有效保留住優秀的個體；另一方面，適應度值一定時，聚合適應度的大小與抗體濃度值呈負相關，體現出免疫系統的自我調節能力，保證了算法的全局搜索能力。

3.3 免疫遺傳算法反演

(1)基因編碼：對于紗線原料性能參數反演問題，實數編碼無法將離散編碼序列和連續微粒位置對應起來，所以本文此處采用8位二進制編碼的方式來對微粒進行編碼。

(2)種群初始化：當反演的參數為兩個時，在一定范圍內隨機產生1行16列的0、1數值矩陣來初始化種群。

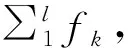
(4)交叉變異：交叉及變異都是形成新個體的一種有效方法，其優點是能夠避免部分信息丟失，最大限度的保證了遺傳算法的有效性。反演算法部分交叉與變異操作采用正演算法部分的相同操作，不同點在于染色體的編碼方式。

(5)基于濃度的群體更新：反演部分群體更新的操作也同正演模型部分的相同，只是此處無需將實數編碼轉換成二進制編碼。

4 仿真實驗

先對免疫遺傳算法優化的BP神經網絡在紗線質量預測上的可行性與效果進行探究，利用來自山東某棉紡廠的29.2 tex精梳純棉紗配棉及棉紗(均是在相同的生產條件下紡成)質量數據。

經過10次訓練仿真后取試驗數據的平均值，最后所得結果如表1所示。

表1訓練結果

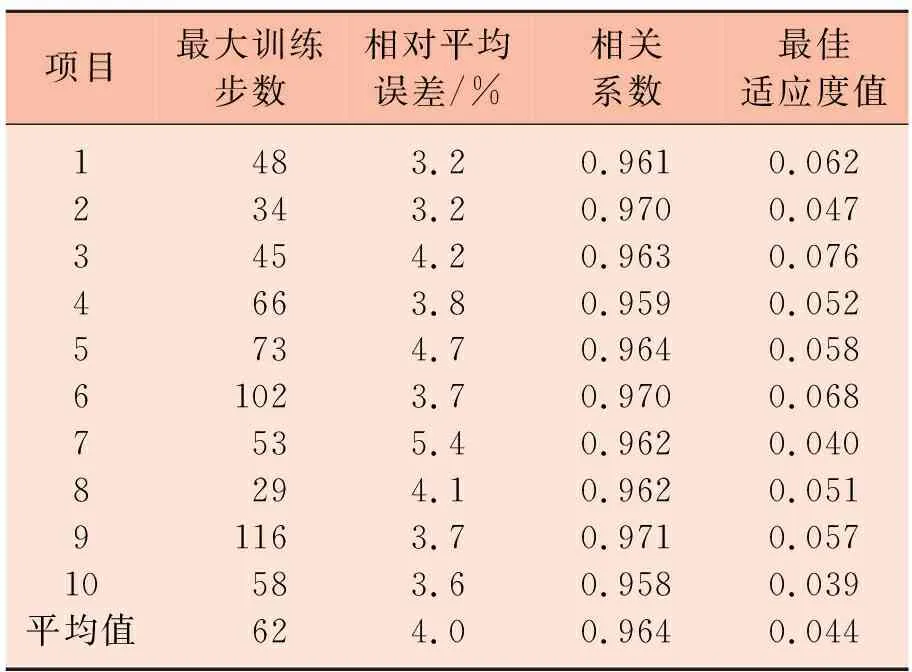
項目最大訓練步數相對平均誤差/%相關系數最佳適應度值12345678910平均值4834456673102532911658623.23.24.23.84.73.75.44.13.73.64.00.9610.9700.9630.9590.9640.9700.9620.9620.9710.9580.9640.0620.0470.0760.0520.0580.0680.0400.0510.0570.0390.044

在2.1設立的BP神經網絡模型的基礎上利用Matlab軟件進行訓練和仿真，BP神經網絡的參數設定如下：訓練步數為1 000，訓練目標為0.000 1，兩次顯示之間的訓練步數為50；另外，網絡的激活函數選擇tansig函數，訓練函數選擇trainlm函數。建立免疫遺傳BP神經網絡模型，對紗線強力值進行預測分析，免疫遺傳算法的參數設定為：種群規模為30，進化代數為50，十進制編碼方式，適應度比率選擇方法，交叉概率為0.8，變異概率為0.2；新增抗體數Z為10，聚合適應度計算公式中常數β設定為-0.6。

如表2所示，其中前30組用于模型訓練，后10組數據用于測試神經網絡。

表2配棉及棉紗質量數據

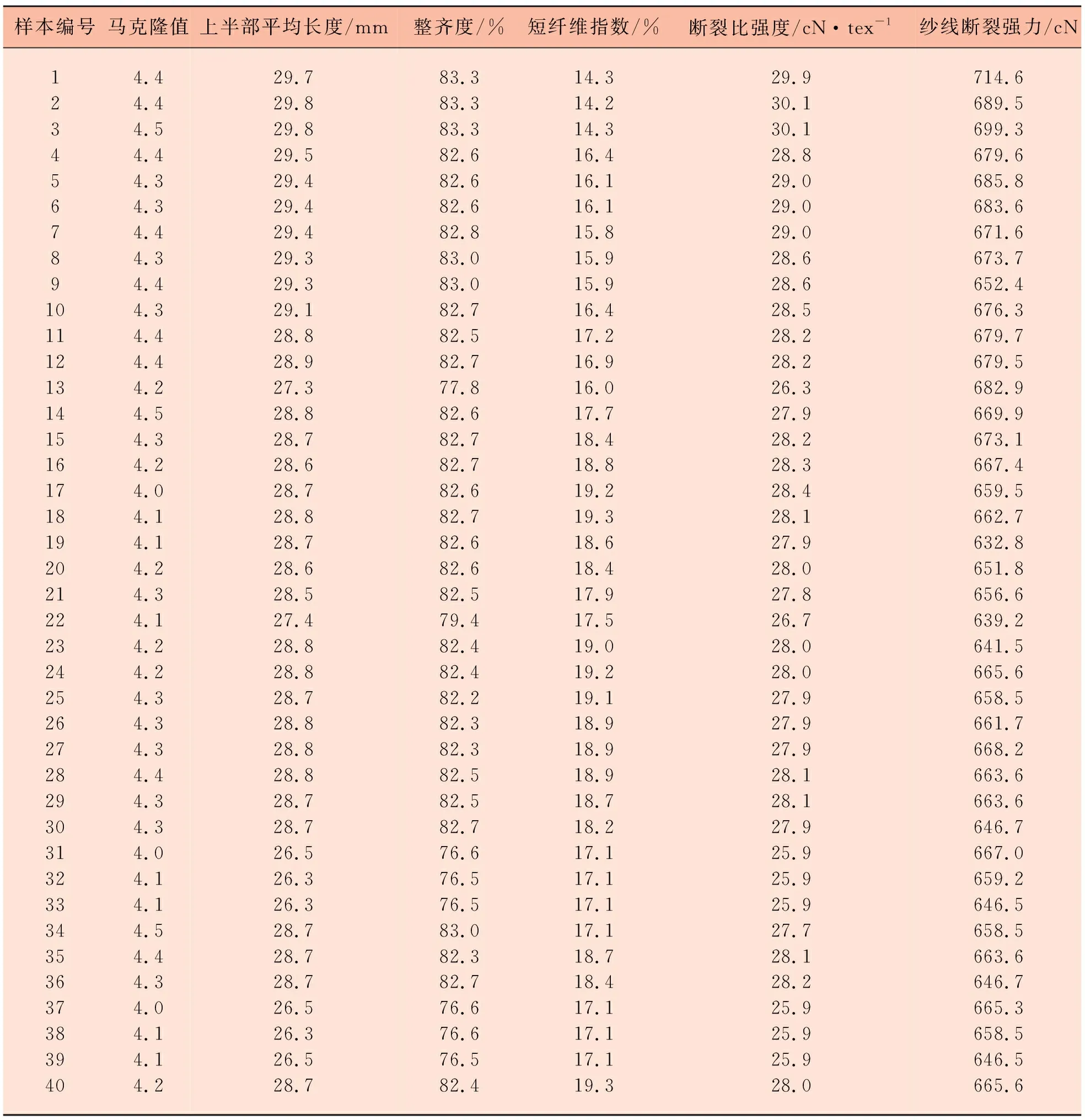
樣本編號馬克隆值上半部平均長度/mm整齊度/%短纖維指數/%斷裂比強度/cN·tex-1紗線斷裂強力/cN123456789101112131415161718192021222324252627282930313233343536373839404.44.44.54.44.34.34.44.34.44.34.44.44.24.54.34.24.04.14.14.24.34.14.24.24.34.34.34.44.34.34.04.14.14.54.44.34.04.14.14.229.729.829.829.529.429.429.429.329.329.128.828.927.328.828.728.628.728.828.728.628.527.428.828.828.728.828.828.828.728.726.526.326.328.728.728.726.526.326.528.783.383.383.382.682.682.682.883.083.082.782.582.777.882.682.782.782.682.782.682.682.579.482.482.482.282.382.382.582.582.776.676.576.583.082.382.776.676.676.582.414.314.214.316.416.116.115.815.915.916.417.216.916.017.718.418.819.219.318.618.417.917.519.019.219.118.918.918.918.718.217.117.117.117.118.718.417.117.117.119.329.930.130.128.829.029.029.028.628.628.528.228.226.327.928.228.328.428.127.928.027.826.728.028.027.927.927.928.128.127.925.925.925.927.728.128.225.925.925.928.0714.6689.5699.3679.6685.8683.6671.6673.7652.4676.3679.7679.5682.9669.9673.1667.4659.5662.7632.8651.8656.6639.2641.5665.6658.5661.7668.2663.6663.6646.7667.0659.2646.5658.5663.6646.7665.3658.5646.5665.6

神經網絡預測模型訓練好以后，通過建立的免疫遺傳算法反演模型反演單纖維斷裂比強度及短纖維指數兩個參數。免疫遺傳算法反演模型主要參數設定為:種群數目M=30，進化代數G=50。每個種群的交叉概率及變異概率在一定的范圍內隨機產生。免疫遺傳神經網絡算法反演迭代結果如圖3所示。由圖3可知，該算法迭代不到10次就已經收斂，最佳適應度函數值維持在0.05左右。反演的結果如圖4和圖5所示。

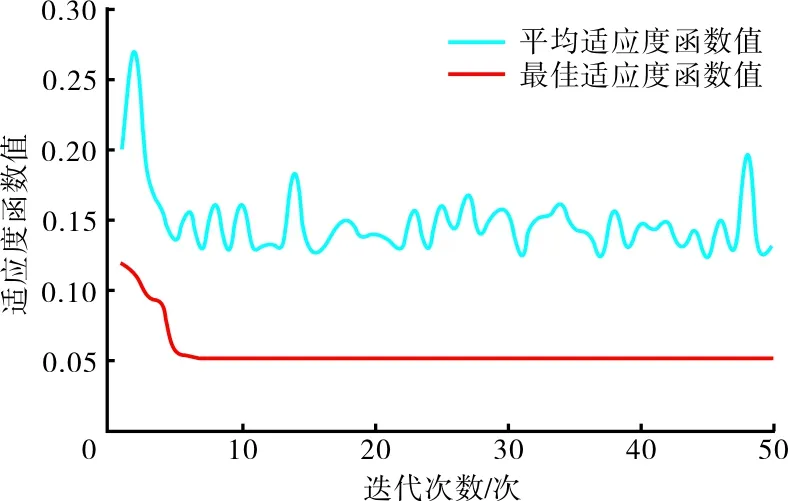
圖3 反演模型適應度函數值迭代曲線

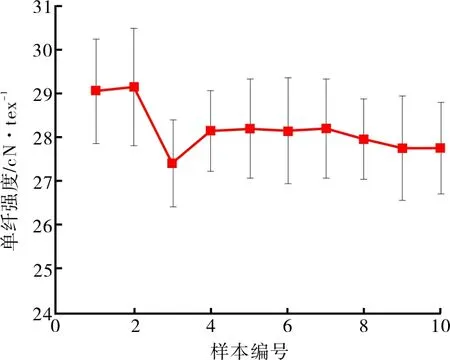
圖4 單纖維斷裂比強度反演模型預測結果

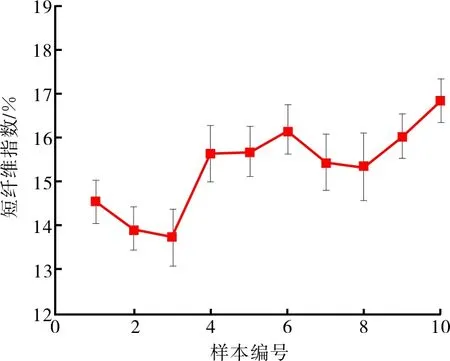
圖5 短纖維指數反演模型預測結果

由圖4和圖5可知，兩個參數的反演精度都很高，預測值十分接近目標輸出，誤差維持在5%左右。

5 結語

針對傳統參數反演算法存在收斂性與穩定性不理想、反演精度較低、計算緩慢以及標準遺傳算法存在的早熟收斂等缺點等問題，本文利用免疫遺傳算法優化BP神經網絡的權值和閾值來建立遺傳神經網絡正演模型，再根據紗線斷裂強力值來反演原棉性能參數，最后以實際紡織生產過程參數進行模型測試，實例驗證了算法的可行性和有效性，反演精度達到95%以上。根據本文的反演結果可調節其動態加工生產過程中的敏感參數，使產品質量達標且工藝組合得到優化，同時對企業新產品工藝開發設計的快速決策也具有很好的借鑒作用。