基于準平衡滑翔的解析再入制導方法
王肖, 郭杰, 唐勝景, 祁帥
(北京理工大學 宇航學院, 北京 100081)
0 引言
高超聲速滑翔飛行器具有速度快、機動能力強、射程遠、精度高等特點,受到世界各國的持續關注[1-2],再入制導一直是其研究難點。再入制導方法分為標準軌跡制導和預測校正制導兩類:標準軌跡制導需要離線設計飛行器的標準軌跡,并在線跟蹤標準軌跡得到制導指令[3],該方法實現簡單、在線計算量小,但依賴于標準軌跡,易受擾動影響,也不利于軌跡的在線規劃;預測校正制導不依賴于標準軌跡,根據在線預測終端值與期望值的偏差實時校正制導指令,預測校正制導對初始誤差和參數攝動具有較強的魯棒性,實時性較好。隨著再入任務對自主性、魯棒性要求的提高,預測校正制導逐漸成為再入制導發展的趨勢[4]。
文獻[5]通過數值預測建立攻角、傾側角與縱程、橫程之間的線性關系,進而校正控制量。文獻[6-10]將過程約束轉化為傾側角幅值約束,然后利用傾側角剖面預測終端待飛航程,并校正傾側角指令。文獻[11-12]設計了兩種分段預測校正制導算法,利用預設航路點將軌跡分段預測,提高了計算效率,但該方法依賴于離線優化,并降低了算法的自主性。文獻[4,13-14]設計并改進了一種適用于各類升阻比飛行器的數值預測校正制導算法,以航程誤差校正傾側角剖面作為基準算法,輔以高度變化率反饋以滿足過程約束。然而,上述方法均屬于數值預測校正制導,需要不斷在線數值積分,對彈載計算能力的要求較高,無法廣泛應用。
相比之下,解析形式的預測校正制導避免了對彈道的數值積分,計算量大幅減少,更有利于彈上實現。文獻[15]研究了零攻角條件下動能彈頭的解析預測制導,但并不適用于高超聲速滑翔飛行器。文獻[16-17]研究了跳躍式再入返回的解析預測校正制導,僅適用于低升阻比飛行器。文獻[18]將升力系數分為3個分量,實現了縱向運動方程、橫向運動方程和速度方程的解耦,求得了滑翔軌跡的解析解,但仍需數值積分。文獻[19]將過程約束轉化為高度- 速度平面內的統一解析式,并給出了可重復使用運載器的閉環解析解,但該方法本質上屬于標準軌跡生成方法。文獻[20]以常值升阻比得到了傾側角和待飛航程之間的解析關系,但不能保證準平衡滑翔條件,也未對終端高度進行嚴格約束。
現有的預測校正制導一般考慮終端能量和航程約束,但約束終端能量并不能嚴格約束終端高度。文獻[21]將攻角、傾側角作為控制量,每個制導周期根據終端航程、高度誤差的加權函數更新控制量剖面,有效減小了終端高度誤差,但該方法仍需數值預測軌跡,在線計算量較大。
此外,如何保證過程約束也一直是預測校正制導的難點,傳統方法一般利用準平衡滑翔條件將過程約束轉化為傾側角走廊[6,22]。然而,再入過程中準平衡滑翔條件不一定嚴格成立,且實際飛行中的大氣環境擾動和飛行器參數的不確定性也使得這種傾側角走廊的可靠性難以保證[23-24]。
基于上述分析,本文提出了一種基于準平衡滑翔的解析制導方法。首先基于常值升阻比假設建立了再入航程與傾側角的解析關系,得到了傾側角指令。然后針對終端高度約束,利用常值航跡角假設建立了終端高度與航跡角的解析關系,得到了航跡角指令,進而通過設計反饋控制律求得攻角指令。對于過程約束,提出了一種在線約束控制方法,將過程約束問題轉化為航跡角指令跟蹤問題。最后,通過數值仿真表明該方法計算速度快、精度較高,且較好地滿足各種約束。
1 制導問題描述
1.1 運動方程
高超聲速滑翔飛行器的三自由度運動方程一般以時間為自變量[3],但由于飛行時間無法事先確定,給彈道積分造成一定困難。為此,本文引入如下能量形式的無量綱變量:
(1)
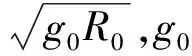
(2)

(3)
式中:λ和φ分別為地球經度和緯度;θ為航跡角;ψ為航向角;σ為傾側角;L為無量綱升力加速度。L和D的計算公式可表示為
(4)
式中:m為飛行器質量;S為飛行器特征面積;CL和CD分別為升力和阻力系數,且是攻角α和速度v的函數;ρ為大氣密度,
ρ(h)=ρ0e-h/hs,
(5)
ρ0為海平面大氣密度,h為無量綱高度,hs=7 110/R0為高度系數。
1.2 再入約束
再入約束一般可分為過程約束和終端約束。典型的過程約束包括熱流密度約束、過載約束和動壓約束,其計算公式分別為
(6)
(7)
(8)
終端約束一般包括終端高度約束、速度約束及經度、緯度約束。由于運動方程以能量為自變量,于是終端約束可表示為
(9)
s(ef)=sf,
(10)
式中:s(ef)為無量綱終端再入航程;sf為再入航程的實際值。s(ef)與sf計算公式分別如(11)式和(12)式所示:
(11)
sf=arccos (sinφ0sinφf+cosφ0cosφfcos(λf-λ0)),
(12)
式中:λ0、φ0為飛行器初始經度和緯度。
2 制導算法
2.1 傾側角解析解
初始下降段飛行高度較高,氣動力作用較弱,通常通過迭代得到常值傾側角進行開環制導,并當滿足一定條件后轉入滑翔段[6,22]。
對于滑翔段制導,考慮終端航程約束及(11)式,再入過程中,特別是滿足準平衡滑翔條件(QEGC)時,航跡角很小,有cosθ≈1,于是有
(13)
利用準平衡滑翔條件:
(14)
可得
(15)
代入(13)式得
(16)
假設再入過程中升阻比已知且為常數, 則以常值傾側角積分(16)式得
(17)
利用(17)式和終端能量及航程約束可求得常值傾側角幅值:
(18)
以上求取傾側角的解析方法是基于再入過程滿足準平衡滑翔條件推導得到的,然而實際飛行可能不滿足準平衡滑翔條件,于是該方法的準確性不能得到保證。為了保證該解析解的精度,同時抑制再入過程中的軌跡振蕩問題,本文在傾側角指令中反饋高度變化率,使升力更快地平衡重力,從而抑制高度振蕩問題,使軌跡滿足準平衡滑翔條件[4],即
(19)
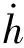
(20)
由于滑翔初始段軌跡振蕩幅值較大,此時傾側角應側重于振蕩的抑制;而滑翔末段振蕩較輕,此時傾側角應側重于航程的校正。故反饋系數k可取為能量的函數:
(21)
式中:k0=30;kf=10;e0為滑翔段初始能量值;et=0.99ef.
以上傾側角解析解的精確程度不僅取決于軌跡是否滿足準平衡滑翔條件,也與常值升阻比假設有關。為此,每個制導周期內需實時更新方程(18)式中的升阻比信息。由于攻角尚未確定,可按上一周期的攻角計算升阻比。隨著飛行器距離目標點越來越近,剩余航程越來越小,升阻比的變化范圍更小,更加接近于常值,傾側角解析解的精度會不斷提高。
2.2 攻角解析解
以終端能量為積分終止條件,根據傾側角解析解可保證終端航程約束和能量約束。傳統預測校正算法一般將終端高度和速度約束轉化為終端能量約束,但保證終端能量并不能嚴格約束終端高度。
進一步考慮準平衡滑翔條件(14)式,再入過程中無量綱地心距r≈1,于是有
Lcosσ+(v2-1)=0.
(22)
觀察(22)式,對于給定終端速度,由于升力加速度L隨高度的增大而減小,此時的傾側角應減小才能滿足準平衡滑翔條件。即終端高度約束對應了一個傾側角。也就是說根據終端航程約束可確定一個傾側角,根據終端高度約束也可確定一個傾側角。當航程約束與高度約束不匹配時,很難通過一個傾側角指令同時滿足終端航程約束和高度約束。然而,(22)式中還隱含另一個控制量攻角,可利用攻角滿足終端高度約束。
首先,由(3)式和(11)式可求得航程對高度的微分:
(23)
(24)
于是可求得滿足高度與航程約束的期望航跡角:
(25)
(25)式得到的是航跡角期望值,與實際值并不相符,需要設計控制律對其跟蹤:
(26)
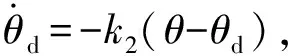
于是得到了期望的航跡角變化率,然后利用航跡角動力學方程:
(27)
求出升力系數:
(28)
進而根據升力系數反插值求出攻角指令。
以上攻角解析解的精確程度主要取決于常值航跡角假設是否合理。滑翔初始段航跡角變化較大,利用上述方法求得的攻角指令可能偏差很大,甚至不在攻角的實際可取范圍內。由于滑翔初始段不需考慮終端高度,正常飛行即可,同時考慮到初始段的熱保護要求和后續的航程要求,采用分段函數形式的攻角方案:
(29)
式中:αm為一個較大的攻角;αL/D為最大升阻比攻角;vm和vL/D為預先設定的速度值。
當滿足e>ep時(ep為預先設定的能量值),攻角指令由方案(29)式切換至由(28)式得到的解析解:
(30)
滑翔后段基本滿足準平衡滑翔條件,軌跡比較平直,常值航跡角假設合理,利用攻角解析解可保證終端高度約束。
此外,為了減小攻角指令由攻角方案切換至解析指令時的突變并保證終端航跡角跟蹤精度,將誤差系數γ設計為
式中:γ0=1;γf=0.75;ep=0.9ef;et=0.99ef.
2.3 過程約束管理
過程約束控制一直是預測校正制導的難點之一。傳統方法一般利用準平衡滑翔條件將過程約束轉化為傾側角走廊,然而,再入過程中準平衡滑翔條件不一定嚴格成立,并且實際飛行中的大氣環境擾動和飛行器參數不確定性也使得這種傾側角走廊的可靠性難以保證。文獻[4]基于時標分離原則提出了一種在線預測約束管理方法。在此基礎上,本文設計了一種基于航跡角指令的在線約束控制方法。
以動壓約束為例,當實際動壓接近最大動壓值即q≥μqmax時,其中μ為接近于1但小于1的常數,可取為0.98,于是設計反饋控制律:
(31)
式中:kq=0.1為動壓反饋系數。于是實際動壓可跟蹤一個給定的期望值,該期望值比最大動壓略小,從而滿足動壓約束。然后對(8)式求微分得
(32)
(33)
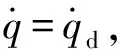
(34)
類似地,可求得滿足熱流約束和過載約束的航跡角指令值:
(35)
(36)
(37)
當實際飛行中的過程約束接近或超過最大值時,根據(37)式求出航跡角指令θc,然后利用(30)式求出相應的攻角指令以滿足過程約束。此過程中產生的終端誤差可在后續的制導周期中得到彌補,從而不影響最終精度。
實際仿真中發現,上述獲得的攻角指令可能存在抖振和不連續問題。為使攻角指令平滑易于跟蹤,將指令進行1階低通濾波:
α(i)=χαd(i)+(1-χ)α(i-1),
(38)
式中:0<χ<1為濾波系數,可取為0.1;α(i)為當前的實際攻角指令;α(i-1)為上一時刻的實際攻角指令;αd(i)為當前由(30)式計算得到的攻角指令。
2.4 側向制導
對于側向制導,本文采用經典的航向角走廊方法確定傾側角符號。設ψLOS為飛行器當前點到目標點的視線角,其計算公式為
(39)
則當前航向角誤差為ψ-ψLOS. 當航向角誤差超過預設的誤差走廊時,改變傾側角符號使其重新回到走廊內,當航向角誤差未超過誤差走廊時,保持傾側角符號不變,即
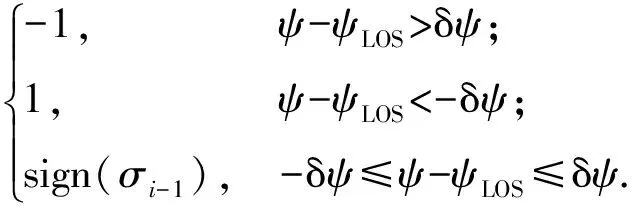
(40)
式中:σi-1為上一時刻的傾側角;σi為當前時刻的傾側角;δψ為航向角誤差門限。
3 仿真分析
本文以通用航空器CAV-H為仿真對象[26]。該飛行器質量907 kg,參考面積0.483 9 m2. 攻角方案參數αm=20°,αL/D=10°,vm=6 500 m/s,vL/D=5 000 m/s,誤差門限δψ=15°,過程約束設置[27]為
(41)
再入任務初始和終端狀態設置如表1所示。
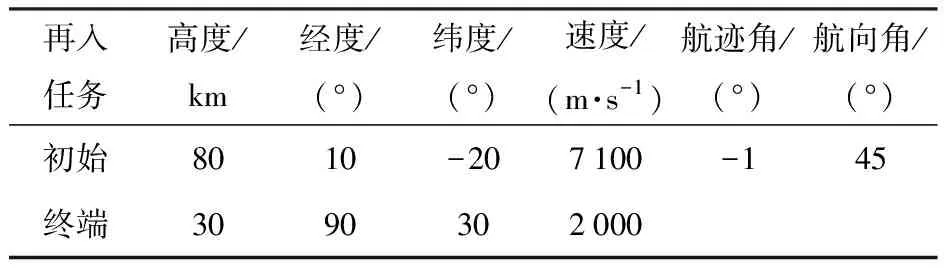
表1 再入任務初始和終端狀態
仿真環境為Windows10操作系統,仿真計算機CPU主頻3.2 GHz,內存4 GB,制導周期為10-4無量綱能量。
3.1 標準條件下制導方法仿真
為了驗證所提出解析制導方法(簡稱方法1)的有效性與優越性,本節將其與文獻[6]中常值傾側角數值預測校正制導方法(簡稱方法2)在標準條件下以相同仿真環境和制導周期作對比。方法2以終端能量為約束,不能嚴格保證終端高度,且未考慮軌跡振蕩問題。仿真結果如表2和圖1所示。
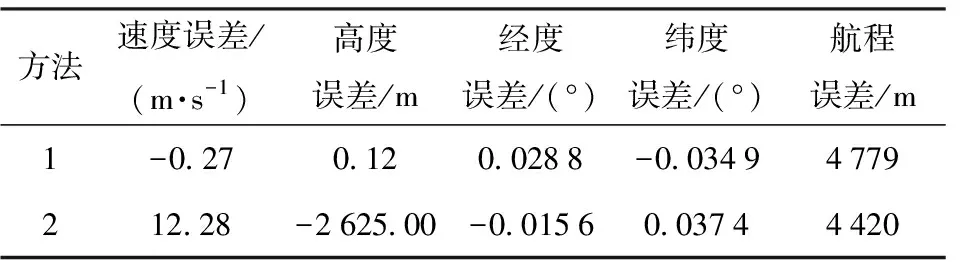
表2 終端誤差
表2為兩種方法的終端誤差。兩種方法的航程誤差均較小,具有一定精度。方法2的終端高度誤差較大,這是因為該方法僅以終端能量為約束,不能嚴格約束終端高度。而本文所提出的方法根據終端高度約束得到攻角指令,終端速度、高度誤差均很小,滿足終端高度約束。圖1為標準條件下的高度- 速度曲線。相比方法2,方法1中由于添加了高度變化率反饋,軌跡更加平滑,無明顯振蕩,基本滿足準平衡滑翔條件,更加適用于高升阻比的高超聲速滑翔飛行器。
圖2為標準條件下的地面軌跡,圖3、圖4分別為標準條件下的傾側角和攻角。方法1的傾側角初始階段變化較大,這是因為為了盡快滿足準平衡滑翔條件,在控制指令中加入高度變化率反饋造成的。相比之下,方法2的傾側角幅值近似為常值。方法2的攻角指令完全按照攻角方案給出。而方法1在滑翔末端為滿足終端高度約束,根據航跡角指令設計攻角指令,使攻角逐漸增大以抬高終端高度滿足終端高度約束。
圖5~圖7分別為標準條件下的各過程約束曲線。兩種方法均可滿足各過程約束,相比方法2,方法1的過程約束變化更加平滑,無周期性振蕩現象且峰值較小,更易于飛行器承受。
圖8為方法1在標準條件下的升阻比和航跡角曲線。由圖8可知,再入過程中,升阻比變化平緩且變化范圍較小,可近似于常值;滑翔段航跡角變化不大,也可認為是常值。隨著飛行器距離目標點越來越近,剩余航程越來越小,升阻比和航跡角的變化范圍更小,更接近于常值,解析解的精度會不斷提高。
此外,在相同的仿真環境和制導周期下,方法1的計算時間比方法2的計算時間小兩個數量級以上,這顯示出解析制導相比數值預測校正制導在計算效率上的優越性。
3.2 擾動條件下制導方法仿真
為了驗證所提出的方法在擾動條件下的精度和魯棒性,進行200次蒙特卡洛仿真。仿真中各初始狀態偏差和參數偏差假設符合正態分布,其偏差限如表3所示。
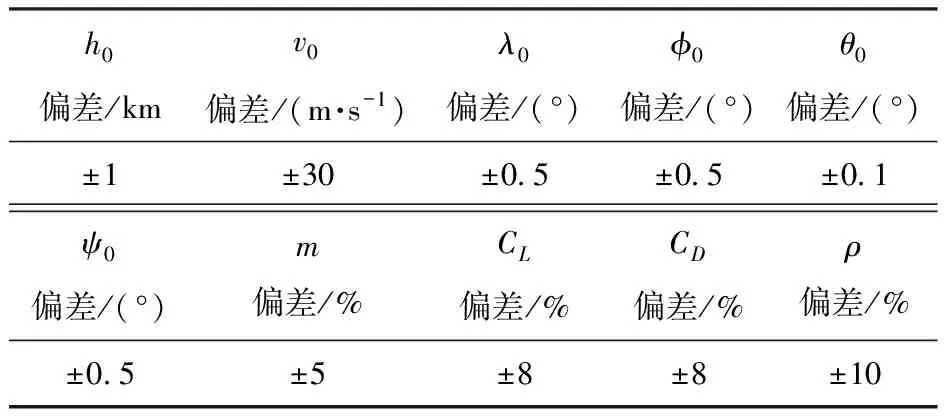
表3 參數偏差
圖9為擾動條件下的高度- 速度曲線。由圖9可見,擾動條件下的軌跡仍比較平滑,基本滿足準平衡滑翔條件。軌跡末端分布較寬,這是調整終端高度造成的。圖10為擾動條件下的終端高度- 速度誤差散布。由圖10可見,終端高度誤差基本在200 m以內,速度誤差在1 m/s以內,仍具有較高的精度。圖11為擾動條件下的落點散布,可見落點基本散布在10 km以內,滿足再入制導要求。
圖12~圖14分別為擾動條件下的各過程約束曲線。本文提出的方法在擾動條件下仍可滿足各過程約束。特別是對于動壓約束,利用本文所提出的在線約束控制方法,實際動壓可嚴格約束在最大動壓150 kPa以內。
4 結論
本文針對高超聲速滑翔飛行器再入制導問題,提出了一種基于準平衡滑翔的解析制導方法。理論分析和仿真結果表明:
1)利用基于準平衡滑翔條件得到的近似解析關系求得的傾側角指令和攻角指令可保證終端航程約束和高度約束,避免了傳統預測校正制導中的數值計算,可為在線制導提供一定參考。
2)反饋高度變化率修正傾側角指令可使軌跡平滑,并滿足準平衡滑翔條件。
3)基于航跡角指令的在線約束控制方法可保證滿足過程約束。
4)該方法在擾動條件下具有一定精度和魯棒性。

