結合深度學習的網絡鄰居結構研究及應用*

寇曉宇，呂天舒，張 巖

北京大學 信息科學技術學院，北京 100871

1 引言

隨著信息網絡規模的急劇增大，網絡數據變得復雜多樣，通過分析和研究網絡的拓撲結構，可以探索到網絡中豐富的知識，進而可以提煉出多種高效的營銷模式。如在微博、Facebook為代表的社交網絡中，一種方式是通過已知的好友關系以及部分屬性已知的用戶推測出未知用戶的屬性，進一步得到用戶在不同屬性類別下的影響力高低，從而利用網絡中具有高影響力的用戶進行高效營銷；另一種方式是通過預測某用戶未來的行為，有針對性地進行個性化營銷等。

網絡中節點的鄰居結構可以描述節點間的復雜交互關系，不同的鄰居結構往往有不同的意義表達。如微博中用戶的關注關系，若某明星A自身有大量粉絲，并且A關注了B，一般情況下，B也是明星或者有高影響力的用戶；若A的大量粉絲沒有任何粉絲，一般情況下說明A有大量“僵尸粉”但實際影響力不高。目前對于網絡拓撲關系的研究中大多數關注直接鄰居組成的結構情況[1-2]或者不同跳數鄰居的數目情況[3]，很少關注不同跳數鄰居組成的結構的影響。為了解決這一問題，本文以三種最為基本的鄰居結構進行分析。圖1給出一個實例，紅色節點為目標節點，鄰居A、B為指向目標節點的直接鄰居，構成兩個第一種鄰居結構；鄰居C、D構成一個第二種鄰居結構，其中鄰居D為目標節點的二度鄰居；鄰居E、F構成一個第三種鄰居結構，其中鄰居F既是目標節點的一度鄰居，也是二度鄰居。因為這三種鄰居結構最為普遍，而且比較有代表性，既包含簡單交互關系，也有復雜交互關系，因此選取這樣三種鄰居結構進行實驗。

網絡中鄰居形成的不同結構有著不同的影響效果：例如在使用微博轉發的數據集進行用戶行為預測時，要判斷圖1的紅色節點即目標用戶V是否會去轉發微博t，V的好友們構成了這三種鄰居結構。若僅僅好友A或好友B轉發了t，對V觸動可能并不大；若t接連被D和C轉發，V會有更大的可能性繼續轉發t；若當t接連被F和E轉發，且E和F有共同好友V，則V也轉發t的可能性更大。

自然語言處理技術與深度學習算法在網絡中的應用越來越廣泛，如網絡表示學習的DeepWalk模型[4]通過隨機游走得到節點序列，最終得到節點向量表示。同時深度學習算法促進了特征自動提取的實現，本文通過結合深度學習卷積神經網絡（convolutional neural networks，CNN）[5]對網絡進行研究。由于直接將鄰居結構輸入到CNN中處理會大大降低運行效率，且CNN更適應于處理圖像數據，因此可以將鄰居結構數據轉換為圖片的格式，提高CNN對數據處理的速度。

本文的主要貢獻包括：

（1）提出了結合深度學習CNN的網絡鄰居結構影響力模型DNSI（neighbor structure influence based on deep learning），并通過自動特征提取的方式得到三種鄰居結構在網絡中的影響力大小。

（2）將鄰居結構數據轉換為便于CNN對網絡數據處理的樣式，即將網絡中節點的不同類別下三種鄰居結構矩陣數據轉換成圖片的像素值，輸入到CNN中進行批量處理。

（3）由模型DNSI得到三種鄰居結構的影響力，在真實世界的網絡數據集上進行節點屬性預測、類別中心度度量以及用戶行為預測，證明該模型在絕大多數情況下都可以提高預測的正確率。

本文第2章介紹使用拓撲結構對網絡進行分析的相關研究。第3章詳細介紹了本文提出的基于深度學習的網絡鄰居結構影響力模型DNSI的原理。第4章為模型在多個真實世界數據集上的實驗結果。最后，是對本文工作的總結和下一步工作的展望。

2 相關工作

本章介紹基于拓撲結構對網絡分析的相關研究，包括傳統的基于拓撲結構進行的網絡研究以及融合深度學習與拓撲結構的網絡研究兩部分。

2.1 傳統的基于拓撲結構進行的網絡研究

（1）對用戶屬性預測

針對社交網絡中用戶會選擇性提供個人信息的情況，He等人[6]提出將好友關系映射出貝葉斯網絡的方法，通過已知的先驗概率對用戶屬性進行推測，可以得到預測為每種屬性的條件概率。而Zhou等人[7]在這基礎上融合了用戶的社交關系，指出不同的社交關系可以推測不同的屬性。Zheleva等人[8]拓展了社交關系，通過可見的群信息來推測用戶屬性。除此之外，Mislove等人[9]提出了基于社區發現的推測用戶屬性算法，該算法可以應用于在線社交網絡，算法思想是相同屬性的用戶更有可能形成聚合度比較高的社區群體。

（2）中心度度量

最常見也最容易理解的中心度度量指標為度中心性（degree centrality）[10]，定義為目標節點的直接鄰居數目，該指標反映出該節點的直接影響力情況。Chen等人[11]將中心度擴展到目標節點的鄰居數目與其鄰居的鄰居數目，即局部中心性（local centrality）指標。在這種思想的引領下，擴展度（ExDegree）指標指出，不同的節點傳播概率，會有不同的度擴展層數，比如：n節點傳播概率很小，則只需計算直接相鄰的鄰居數目，而m節點概率較大，則可能要計算三度以內鄰居數目，且一度鄰居數目計算三次，二度鄰居數目計算兩次，三度鄰居節點只計算一次。在此基礎上，Fowler等人[3]定義節點的三度以內的鄰居都屬于強連接關系，三度以上的鄰居不會被影響，即三度影響力原則。

另兩個常見的反映節點拓撲特性的指標是介數中心性（betweenness centrality）[2]與緊密中心性（closeness centrality）[12]，介數中心性是指目標節點在網絡中任意兩個節點的最短路徑上的數目，緊密中心性是指某節點到達網絡中所有其他節點的總距離除以步數。由于這兩個方法復雜度都比較大，不適合于大型的網絡，因此人們提出很多改進方法，如Kitsak等人[13]提出的K-核分解算法，通過把網絡中所有節點從核心到邊緣分層，來定義影響力的大小。而Lv等人[14]通過研究提出H指數（對期刊或者作者進行影響力評價的指標）與K-核在衡量節點影響力方面有類似的效果。

（3）用戶行為預測

對社交網絡中用戶行為的分析最早出現在復雜性科學、統計物理等領域，如Zhou等人[15]進行人類行為特征的研究綜述。除此之外，Zaman等人[16]利用協同過濾方法，通過對博客的用戶轉發數據集進行分析，從而得到用戶轉發的概率。受到上面這些思想的啟發，Tang等人[17]深入研究了微博上用戶的轉發數據，剖析鄰居節點形成的拓撲結構，發現已轉發過某消息的鄰居節點形成的連通圖個數會對目標節點產生影響，從而提出局部節點影響力（social influence locality）模型，并證明在已轉發某消息的鄰居數目相同的情況下，形成的連通子圖數目越少，目標節點也轉發該消息的可能性就越大。進而又提出在動態網絡上不同的鄰居結構對目標節點的行為有不同的影響力，即StructInf模型[18]，并通過對微博數據的邊采樣和節點采樣，得到了20種鄰居結構的影響力。本文中的模型便是受到StructInf模型的啟發，對其鄰居結構進行分類簡化，使用深度學習得到鄰居結構影響力，并對其應用范圍進行了擴展。

2.2 融合深度學習與拓撲結構的網絡研究

2.1節所述的相關研究由于受到特定因素的影響，會有一定局限性，比如網絡規模較大、網絡結構變化大等因素。如StructInf模型需首先進行邊采樣和節點采樣，然后通過統計方式計算其鄰居結構影響力，計算量龐大。而隨著深度學習的深入人心，將深度學習算法融入傳統網絡拓撲結構的研究不斷涌現，相比較傳統的網絡研究方法，其優越性一方面體現在準確率的提升，另一方面體現在算法運行速度的提高。如DeepWalk算法[4]在自然語言處理的啟發下，通過在網絡中隨機游走地選擇節點與邊，把網絡轉換成一系列“句子”，其中單詞代表節點，從而可以利用自然語言處理中的skip-gram模型[19]，將單詞（節點）轉換為表示向量，進而對網絡分析。LINE模型[20]在DeepWalk的基礎上，融合了節點的鄰居結構，提出網絡中存在的兩種相似性，第一種是first-order，即兩個節點直接有邊相連則為相似；第二種是second-order，即兩個節點的共享鄰居數目越多，相似性越高。通過兩種相似性學習得到的兩種向量表示的拼接，可以得到節點的特征表示，從而可以進行網絡研究。

3 基于深度學習的鄰居結構影響力研究

本文提出基于深度學習的網絡鄰居結構影響力模型DNSI，該模型利用CNN算法進行特征提取，得到三種鄰居結構的影響力，從而進行節點屬性預測、類別中心度度量以及用戶行為預測三類實驗。本章首先給出模型相關定義，然后詳細介紹模型的實現，并進行實例講解，最后對模型的復雜度進行討論與分析。

3.1 相關定義

該模型首先統計出網絡中所有節點的三種鄰居結構的數目，輸入到CNN中構建深度網絡，通過特征提取得到三種鄰居結構的影響力，根據這三種影響力可以反映節點在不同圖中的不同特性。

定義1（網絡圖）記G=(E，V)表示一個有向網絡圖，其中V代表節點v的集合，即V={v1，v2，…，vn}，E代表邊ei，j的集合，即所有從節點vi指向節點vj的邊集合為E={ei，j}。記f:vi→cj表示一個映射函數：節點vi的類別為cj，D={f1，f2，…，fn}表示節點的類別映射函數的集合，C={c1，c2，…，cn}表示C為所有類別的集合，其中|C|＜＜|V|。

節點的類別在現實世界數據集中有多重解釋，例如：在生物數據集中，類別可以代表不同的種群；在用戶關注數據集中，類別可以代表用戶不同的屬性；在微博轉發數據集中，類別可以代表用戶不同的行為等。

定義2（一度鄰居結構）在有向圖G=(E，V)中，記目標節點為vn，若vn的直接前驅點vi沒有任何前驅，則vi構成一度鄰居結構。本文中一度鄰居結構對目標節點的影響力記為w1，類別都為cj的鄰居構成的一度鄰居結構的個數記為mj，1。

定義3（二度鄰居結構）在有向圖G=(E，V)中，記目標節點為vn，若vn的直接前驅點vi的前驅vj不指向vn時，則vi與指向vi的前驅節點vj組成了二度鄰居結構。本文中二度鄰居結構對目標節點的影響力記為w2，類別都為cj的鄰居構成的二度鄰居結構的個數記為mj，2。

定義4（加強二度鄰居結構）在有向圖G=(E，V)中，記目標節點為vn，若vn的直接前驅點vi的前驅vj也指向vn時，則vi與指向vi的前驅節點vj組成了加強二度鄰居結構。本文中加強二度鄰居結構對目標節點的影響力記為w3，類別都為cj的鄰居構成的加強二度鄰居結構的個數記為mj，3。

3.2 模型描述

記需要預測類別的目標節點為vn，其真實類別為ck，且整個網絡圖G中的類別總數|C|，則模型目的是學習出最合適的w1、w2、w3，使得vn被預測為自身類別ck的概率最大，即本模型的總體優化目標函數為：

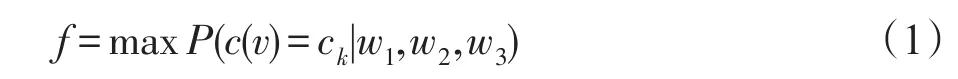
P表示當三種鄰居結構權重為w1、w2、w3時，vn類別預測為ck的概率，即最大化屬于第ck類的鄰居構成的三種結構數目與三種影響力的內積和與其他類別cq鄰居結構數目與影響力的內積和的差值，具體公式如下所示：

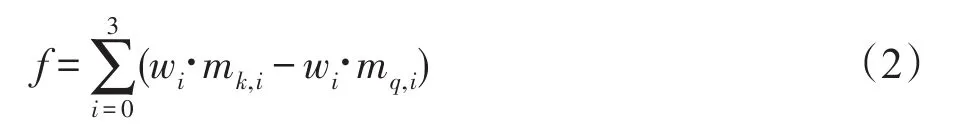
其中，mk，i指屬于第ck類的鄰居組成第i種結構的數目，同理mq，i指屬于第cq類的鄰居組成第i種結構的數目。從而使得節點被預測為自身真實類別的概率最大。

整個模型主要分為兩部分，經過前兩種算法可以得到三種影響力，第三種算法是對節點屬性預測，第四種算法是對節點進行類別中心度度量。

算法1三種鄰居結構數目的確定

算法1中第4行的L存儲了目標節點不同類別的前驅節點；第7行設置flag以及第13行和16行的remove的原因是確保每個鄰居節點只能參與到一種鄰居結構中。

算法2數據處理與CNN網絡層的構建

算法2中第1～5行把節點鄰居結構數目矩陣轉換成一張張圖片的格式，可以加快算法處理速度。第4行說明每張圖片的長為|C|個像素，寬為3個像素。第6行得到CNN的輸入，X可以看作以圖片的形式表示的數據集的特征，Y是每個節點的類別，即數據集的標簽。第7行按照給定的切分比例分出訓練集和驗證集，第8行構建CNN網絡，共1個卷積層，3個全連接層，kernal設置為1×3，網絡其他具體參數在實驗部分討論。第10～14行定義批處理函數，每次迭代過程中按批次取數據，然后進行交叉驗證得到最高的準確率時的卷積層的kernel值，即為三種鄰居結構的影響力。

算法3對網絡節點類別的預測

算法4類別中心度度量

例如圖1中所示的一個有向圖G，紅色的為目標節點vn。已知有6個鄰居節點A、B、C、D、E、F，組成了兩個一度結構，1個二度結構，1個加強二度結構，若G中|C|=3，分別為0類、1類、2類，且vn的真實類別是2類。0類在圖中是橘色，1類為藍色，2類為綠色。則根據算法1可得，Q[vn][0]=[2，0，0]，Q[vn][1]=[0，1，0]，Q[vn][1]=[0，0，1]，若已知根據算法 2 得到的w1、w2、w3為[1,2,3]。若進行類別的預測，則根據算法3可得，P[vn]=[2，2，3]，則c′=2 ，即目標節點被預測為2類。若是進行類別中心度度量，則根據算法4可得，T[vn]=[2，2，3]，即目標節點在第0類的中心度為2，在第1類的中心度為2，在第2類的中心度為3。

3.3 復雜度分析

算法的復雜度分析分為時間復雜度與空間復雜度。本模型主要是要保存所有節點的三種鄰居結構的數目，因此空間復雜度主要受網絡中節點數目影響，即O(|V|)。時間復雜度需要對四種算法分別分析：

算法1的時間復雜度為O(|E|×|V|×|C|)，因為算法需要循環所有節點進行計算鄰居情況，計算每個節點的鄰居情況時只需要循環一遍網絡所有的邊并分別保存在不同的類別下即可。又因為類別數|C|是一個較小的常數，所以算法1的時間復雜度可以看作是與節點數與邊數乘積成線性相關的。

算法2的時間復雜度為O(k×|V|×|C|)，其中k指CNN網絡層的參數對網絡的影響，若層數增加或者增加批量訓練數據的大小就會有相應影響，但是主要還是受節點數目的影響。其次，Batch_size和Epoch的正確選擇也影響內存效率與內存容量之間的平衡。

算法3和算法4的時間復雜度都為O(|C|)，對于每個節點來說，時間復雜度是常數。若是整個網絡所有節點計算的話，時間復雜度即與節點數目成線性相關。

4 實驗結果

本章首先介紹模型的參數設置以及對比算法，其次是評價指標和數據集介紹，最后在多個真實網絡數據集上進行分析實驗，并進行參數敏感性分析。

4.1 實驗設置

通過在真實網絡數據集上實驗發現，節點數目少于1 000個時，學習率大小、批處理大小等都應相對減少，權重初始化的方式也應變化。多次實驗后得到表1中最優的參數設置，即算法2中構建CNN的具體參數。表中第二行是指在網絡中節點數目大于等于1 000個時使用的參數集合，第三行是指節點數目小于1 000個時使用的參數集合。

Tabel 1 Parameter setting in algorithm 2表1 算法2中的參數設置

對于模型將要處理的三類任務，將分別與不同的算法進行對比，其中主要包括下面幾種算法：

（1）KNN算法：該方法是機器學習算法的一種，根據最接近目標節點的k個鄰居情況來判斷目標節點的類別，預測目標節點的類別為占比例最大的鄰居類別。

（2）ExDegree算法：擴展度算法，不同的傳播概率需計算不同的層數的鄰居節點數目，將對不同類別的鄰居分別進行統計。本次實驗中將采用原始論文中的參數，傳播概率0.01到0.15之間，最大擴展度為8，30次獨立實驗取平均結果，節點將被預測為其中概率最高的類別。

（3）StructInf算法：鄰居結構影響力算法，使用作者公布的源代碼，按照原始論文中的采樣參數，q=0.9，px=0.6，py=0.1，先得到20種鄰居結構的影響度，然后對未知用戶的行為進行預測。

（4）DeepWalk算法：通過在網絡圖中進行隨機游走得到節點序列，輸入到skipgram模型中得到節點向量表示，并進行多標簽預測任務。全部使用原始論文中默認的參數進行實驗。

4.2 評價指標與數據描述

本次實驗包括三部分，分別使用不同的評價指標。

（1）節點屬性預測

該任務使用正確率（Accuracy）與平均準確率（mean average precision，MAP）作為評價指標，分別定義如下：

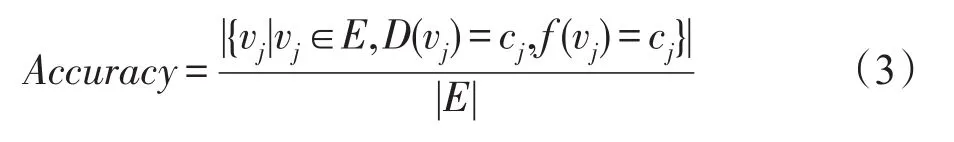
其中，f(vj)是指vj被預測為哪一個屬性，D(vj)指vj實際上為哪一個屬性，分子表示屬性被預測正確的節點。正確率表示為預測正確的節點數目與網絡所有節點數目的比值。

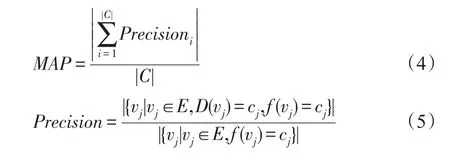
其中，Precisioni表示某個屬性被預測正確的節點數目與所有被預測為該屬性的節點數目的比值，則MAP表示所有屬性準確率的和與網絡中屬性類別總數的比值。MAP指標目的是為了彌補網絡中很多節點由于缺少前驅節點而導致正確率較低的現象。

（2）類別中心度度量

該任務使用算法總運行時間Time與平均前k召回率M_Recall@k作為評價指標，平均前k召回率定義如下：

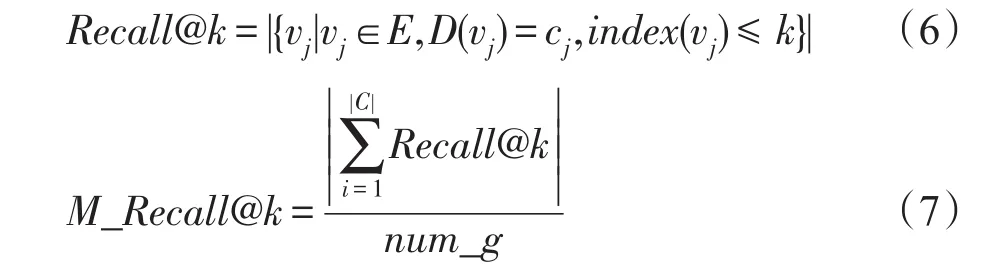
其中，index(vj)是指節點按照預測的中心度從高到低排序的序號，則Recall@k指模型得到的cj類別的前k個節點中真正屬于高中心度節點的個數。num_g指針對某個數據集已知的高中心度的節點數目。則平均前k召回率指所有類別的Recall@k的和與num_g比值。

（3）用戶行為預測

該任務使用正確率（Accuracy）、平均準確率MAP、時間Time、最大加速比MRa作為評價指標，其中MRa指其他算法與本實驗中模型運行時間的比值的最大值。

本實驗中使用的數據都為真實世界數據集，包括公開數據集與爬取的微博數據兩部分，具體情況見表2。表中“實驗”一列的“1”表示進行節點屬性預測，“2”表示類別中心度度量，“3”表示用戶行為預測。其中，Biological_tim[21]為美國生物數據集；Bcspwer10[21]為美國電網數據；Fpga_dcop1220[21]為電路仿真網絡；Facebook_4039[21]為社交網絡數據集；Cite（http：//www.nber.org/patents/）為美國專利引用網絡的子圖；weibo為爬取的新浪微博用戶互相關注網絡，以及這些用戶在10天內發布微博與轉發微博的情況（所有的微博都屬于“同桌的你”“房價”“霧霾”“華為”四個主題之一，若用戶未發布或者轉發這四個主題，則類別為“0”，因此共五種類別）。

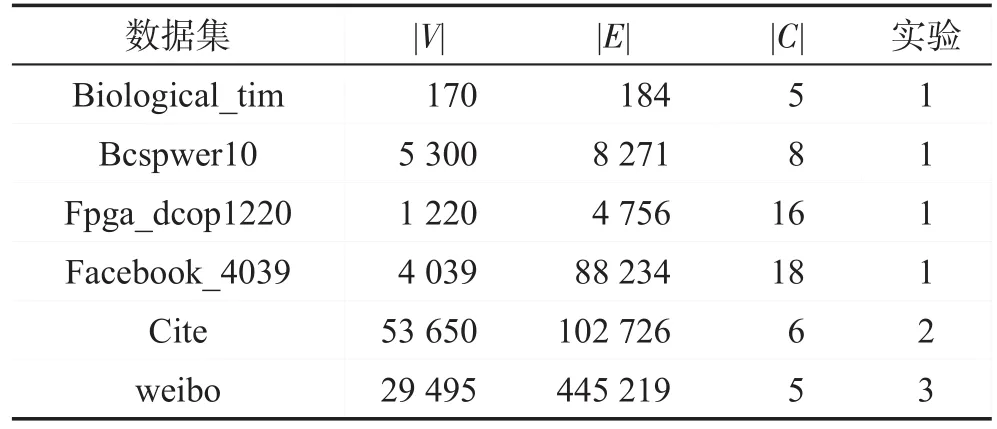
Tabel 2 Datasets information表2 數據集統計信息

4.3 實驗結果與分析

4.3.1 節點屬性預測

節點屬性預測實驗中每個數據集都是選擇80%的數據作為訓練數據，其他作為測試數據。正確率和MAP指標結果見表3，對于Biological_tim小數據集，參數參考表1中的第3行。其他數據集的參數參考表1中第2行。其中KNN算法使用k=2和k=5分別做實驗，較為全面，具有代表性。

從結果可以看出，DNSI模型除了在Biological_tim數據集的MAP和Fpga_dcop1220數據集上的正確率略低于其他模型，其余的效果均好于其他模型。尤其是Bcspwer10數據集上，正確率超過其他幾種模型的13%左右，這說明DNSI在對節點屬性預測任務上有很好的效果。其中在Biological_tim小數據集上，幾種算法的正確率都比較低，通過分析原始數據發現，很多節點缺少前驅節點，因此會出現無法預測的情況。Fpga_dcop1220數據集的效果普遍都比較高，特別是KNN時得到最高正確率，說明數據本身屬性和鄰居節點屬性相關性非常大。而算法KNN中k=5時的結果往往不如k=2時的好，分析認為鄰居擴展太大，不同屬性的鄰居數目混雜造成的誤差。

Tabel 3 Node attribute prediction results表3 節點屬性預測結果

Tabel 4 Category central metric results表4 類別中心度度量結果

4.3.2 類別中心度度量

類別中心度度量實驗使用的是美國專利引用數據集，可以較好地體現DNSI在大數據集上的優越表現。為了高效地召回中心度較高的節點，本次實驗只取入度大于100的節點組成的子圖作為數據集。其中，取專利的技術領域作為類別，取從1963年開始，前800個被引用次數最高的專利作為真實的高中心度節點，即式（7）中的num_g=800。

與KNN、ExDegree、Betweenness centrality、Closeness centrality四種算法進行對比實驗的結果見表4。從結果可以看出，除了在k=40時，絕大部分情況下DNSI算法都可以得到最高的召回率。特別是在k=10時，DNSI算法可以達到10%召回率，說明同其他四種算法相比，DNSI可以更為準確地召回中心度最高的節點，且DNSI算法的運行時間最短，相比于其他的算法有穩定的優越性。

4.3.3 用戶行為預測

用戶行為預測實驗采用爬取的weibo數據。由于微博具有時效性，為了分析三種算法預測的準確性，通過前k天的用戶關注網絡和轉發情況，來預測第k+1～第10天的用戶轉發情況（其中，2≤k＜10）。首先對weibo數據進行預處理，將轉發信息中包含“同桌的你”“房價”“霧霾”“華為”這4個主題的類別設置為“1～4”，其他未轉發這4類主題微博的用戶行為類別設置為“0”，然后預測用戶是否會轉發微博以及轉發哪一類微博。

DNSI模型使用表1中第2行的參數。StructInf、DeepWalk模型使用原始論文中的參數，并針對算法專門調整數據格式，使用戶關系數據和用戶行為類別數據適應算法的輸入格式，通過前k天的數據得到20種結構的影響概率，從而計算出第k+1～第10天的用戶轉發不同類別的微博的可能性，取最大的為預測值。

從表5中的結果可以看出，隨著k的增長，三種算法的時間都不斷增長，但是StructInf算法運行時間普遍較長，DNSI與StructInf算法的最高加速比可達6.43。當k小于6時，DNSI算法的正確率和平均準確率一般都比較高，但是當k大于6時，StructInf算法的正確率普遍較高，但是MAP不如DNSI。而DeepWalk模型的正確率和平均準確率都比較低，可能是受到數據本身的影響，因為數據中有很多節點沒有前驅節點，所以在進行多標簽分類時結果較差。三種算法的正確率最高就到80%左右，且與MAP的差距比較大，也是由于節點缺少前驅節點的原因。

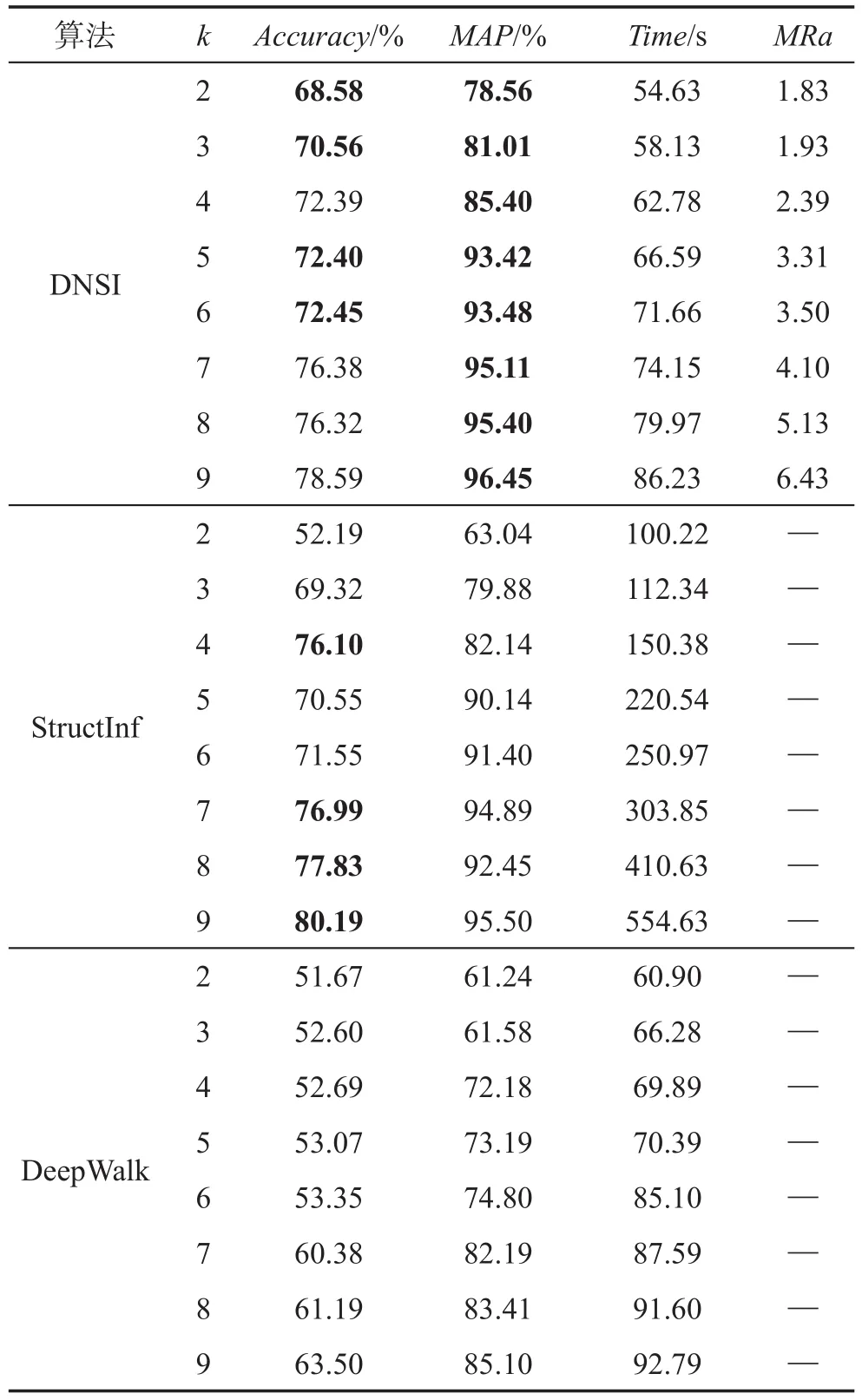
Tabel 5 User behavior prediction results in weibo dataset表5 微博數據集中用戶行為預測結果

六個數據集的三種鄰居結構影響力如圖2所示。為了使不同數據集的鄰居結構影響力可以互相比較，將w1、w2、w3按比例縮放到0～1之間，且w1+w2+w3=1。可以發現，除了facebook數據集的加強二度鄰居結構影響力比較低之外，其他數據集都是加強二度鄰居結構影響力最高，說明關系密切且進行交互行為比較頻繁的鄰居組成會對目標節點影響更大。

4.4 參數敏感性分析

本節度量了Batch_size、Learning_rate和Kernelinitialization三個參數對模型的影響。實驗過程中，除當前被測試的參數，其他參數均保持默認值，即表1中的第二行。測試任務使用Bcspwer10、Facebook_4039、weibo三個數據集，分別進行交叉驗證求平均正確率和平均迭代次數來展示效果。

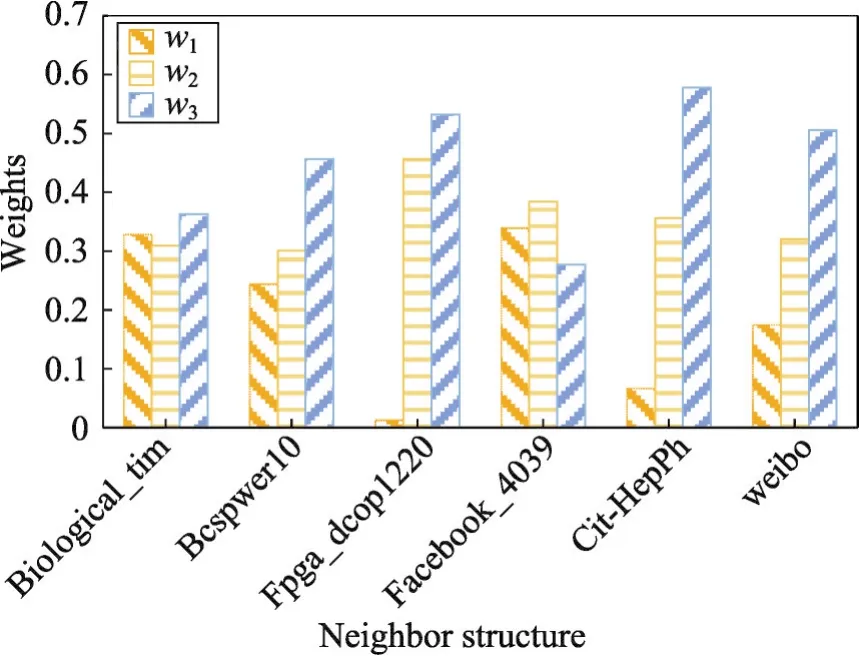
Fig.2 3 neighbor structures'weights of 6 datasets圖2 六個數據集的三種鄰居結構影響力

首先評估Batch_size對模型的影響，結果如圖3所示：Bcspwer10和weibo數據集是隨著Batch_size的增加，模型的正確率先升高后降低，在300～500次之間達到最高。原因是：當批處理數據太少時，梯度更新頻繁，不容易收斂；當批處理數據過多，梯度的更新難以達到最好的效果。而Facebook_4039數據集在Batch_size為100時達到最優效果，且Batch_size>400后無變化，分析數據發現由于Facebook_4039數據集的類別太多，導致每種類別下的節點數目相對較少，因此當Batch_size>400時，相當于是全部數據一起輸入了。

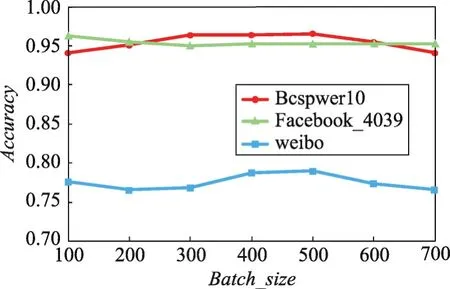
Fig.3 Influence of batch_size on accuracy圖3 批處理數據大小對正確率的影響

Learning_rate對模型收斂速度的影響結果如圖4所示：當學習率非常小時，模型需要迭代多次才能達到收斂，當學習率在0.01時，模型在三個數據集上迭代的次數都是最少的，而當學習率大于0.01時，模型無法收斂，會出現在極值附近“搖擺不定”的現象。

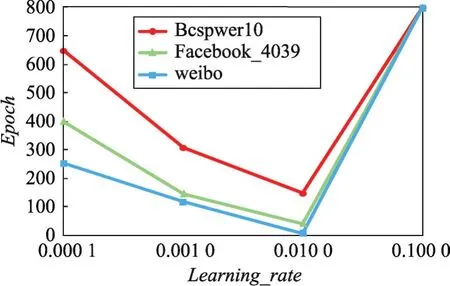
Fig.4 Influence of learning_rate on DNSI convergence rate圖4 學習率對DNSI收斂速度的影響

以Bcspwer10數據集為例分析不同參數組合下權重初始化對模型的影響。第一種權重初始化方式是truncated_normal即正態分布，并設置均值為0；第二種是random_uniform即隨機初始化，并設置最小值為0。表6為4組參數組合，圖5是對模型收斂速度的影響，圖6是對模型正確率的影響。從結果可以看出隨機初始化收斂速度相對較快一些，但是正確率總體相對較低。

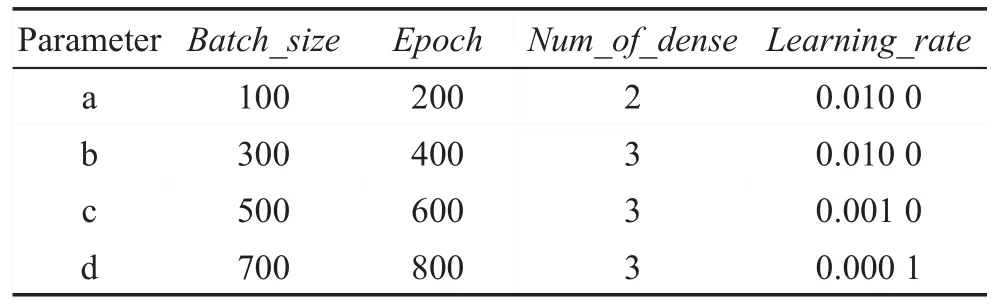
Tabel 6 Parameter choice表6 參數選擇

Fig.5 Influence of weight initialization method on convergence speed圖5 權重初始化方法對收斂速度的影響

Fig.6 Influence of weight initialization method on accuracy圖6 權重初始化方法對正確率的影響

5 總結與展望

本文提出了基于深度學習的網絡鄰居結構影響力模型DNSI，它可以通過自動提取特征得到三種鄰居結構的影響力，并根據這三種影響力進行節點屬性預測、類別中心度度量和用戶行為預測。通過在多個真實網絡數據集上進行的實驗，證明了DNSI在不同的應用場景下都可以有優秀的表現。并且發現普遍情況下，加強二度鄰居結構的影響力最高，也間接說明網絡中節點聯系越緊密，交互行為越頻繁，對目標節點的影響就越大。

下一步，將從以下幾方面繼續嘗試：

（1）除本文三種鄰居結構外，繼續拓展鄰居節點的度數，比如三度、四度鄰居結構等。

（2）除CNN深度學習方法外，嘗試結合其他深度學習算法，得到更為精確的鄰居結構影響力。

（3）更好地利用不同的鄰居結構影響力。本文已經證明通過不同鄰居結構影響力可以進行節點屬性預測、類別中心度度量和用戶行為預測，在其他的方面可能也會有較大的潛力，可以繼續進行應用研究。