Holt-Winters與ARIMA模型在電離層總電子含量預報中的比較

唐 宏,唐詩華,陳雨田,田祥雨

(1.桂林理工大學 a.測繪地理信息學院;b.廣西空間信息與測繪重點實驗室,廣西 桂林 541006;2.深圳市中地軟件工程有限公司，廣東 深圳 518057)

電離層總電子含量(TEC)值直接影響電離層延遲的大小, 精確測定與預報TEC值對于建立精確的電離層延遲改正模型具有十分重要的意義[1]。 目前常用的對TEC值進行預報的方式有兩種: 一種是利用來自經驗或半經驗模式的TEC數據建立起反映TEC值變化規律的經驗公式, 從而建立預報模型, 如Klobuchar模型[2-5]、 IRI模型[6-7]等; 另一種是利用高精度電離層TEC資料采用數理統計方法來建立預報模型, 如神經網絡模型[8-9]、時間序列模型[10]等。其中時間序列模型由于其樣本要求少、計算過程簡單、外延性好等優點,逐漸受到國內外學者的關注,并取得了一些成果。盡管現有的一些研究中利用時間序列模型對TEC值進行預報取得了不錯的效果,但是這些研究并未充分考慮外在因素對預報精度的影響,如太陽活動、緯度、預報時長等。因此,研究這些因素對模型預報精度的影響規律,對于更好地建立和完善TEC預報體系具有十分重要的意義。自回歸積分滑動平均模型(ARIMA)[11-15]計算簡單操作方便, 并且具有較高的預報精度, 是時序方法中應用較為廣泛的一種模型。 Holt-Winters[16-17]可以同時處理趨勢性和季節性變化, 并能夠過濾掉隨機波動的影響, 適用于包含趨勢季節變化的時間序列預測問題。

本文采用ARIMA模型、 Holt-Winters加法模型、 Holt-Winters乘法模型3種時間序列模型, 利用IGS中心發布的不同太陽活動情況下、 不同緯度位置的TEC樣本數據預報不同時長的TEC值, 并將預報值與IGS中心提供的數據進行對比, 在分析上述3種時間序列模型預報精度的同時, 還研究了太陽活動、緯度位置、預報時長這3種因素對模型預報精度的影響。

1 ARIMA(p,d,q)模型原理

ARIMA模型的數學表達式為

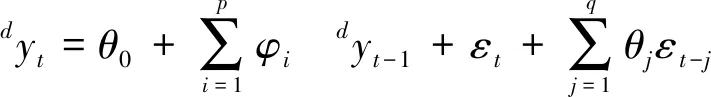
(1)

ARIMA模型本質上是回歸移動平均模型(ARMA)的擴展,通過將非平穩時間序列yt進行d階逐期差分使yt變得平穩, 從而能夠利用ARMA(p,q)模型對該序列建模,然后再經過逆變換得到原序列。上述過程便是ARIMA模型的建模方法。具體的建模步驟為: ① 序列的平穩化處理: 如果原序列是非平穩的, 則需要對其進行差分變換得到平穩序列yt； ② 模型識別: 利用自相關系數和偏相關系數來確定模型的階數p和q； ③ 參數估計與檢驗: 估計模型的未知參數φi和θj, 并且檢驗其顯著性和合理性； ④ 分析預測:利用模型進行預測和分析。

2 Holt-Winters模型原理

Holt-Winters模型將具有趨勢性、 季節性變化和隨機波動的時間序列進行分解, 結合指數平滑方法來建立預報模型, 以對趨勢性和季節性變化作出預測, 包括無季節模型、 加法模型、 乘法模型3種, 其中后兩種適用于具有季節性變化的時間序列預報問題。考慮到電離層的季節性變化,本文采用加法模型和乘法模型來進行TEC值的預報。

Holt-Winters加法模型基本公式

(2)

加法模型的初值計算公式為

(3)

Holt-Winters乘法模型基本公式

(4)

乘法模型的初值計算公式為

(5)

式中:Xt、St、It和bt分別為t時刻的觀測值、 穩定成分、 季節成分和趨勢成分,t=1,2,3,…,L;m為預測期數;Ft+m為第m期預測值;L為季節長度;α、β、γ為平滑參數。

3 太陽活動周期變化

研究表明,太陽活動呈現出以11年為周期變化[18],由圖1(https://omniweb.gsfc.nasa.gov/)中太陽黑子相對數的27天均值變化可以看出2011年正處于太陽活動的上升期,其太陽黑子相對數急劇增加,而2009年的太陽黑子相對數小于10,該年處于太陽活動的平靜期。

太陽的周期性活動會對不同緯度地區的電離層TEC值造成不同的影響,使得預報的效果降低,考慮到這一因素,將上述模型進行對比實驗,分析各個模型受太陽活動的影響,并比較其在不同年份、不同緯度地區的預報精度。

4 實驗分析

4.1 數據準備

太陽活動具有11年左右的周期,第24太陽活動周開始于2008年末,從2010年開始太陽活動明顯增強[19-20]。也就是說，2009年處于太陽活動的平靜期,2011年處于太陽活動的活躍期[18]。因此,選取IGS中心發布的2009年年積日151—165高緯度(75°N, 110°E)、 中緯度(35°N, 110°E)、 低緯度(7.5°N, 110°E)數據作為電離層平靜期樣本序列; 選取2011年年積日101—115高緯度(75°N, 110°E)、 中緯度(35°N, 110°E)、 低緯度(7.5°N, 110°E)數據作為電離層活躍期樣本序列。利用前15天的數據作為樣本序列, 分別采用ARIMA模型、 Holt-Winters加法模型、 Holt-Winters乘法模型預報后5天的TEC值, 并將預報結果與IGS發布的TEC觀測值進行對比。 通過定義相對精度P、 日均相對精度P′和均方差RMS來衡量預報精度

圖1 2000—2017年太陽黑子相對數27天均值變化Fig.1 27 days mean relative sunspot numbers from 2000 to 2017

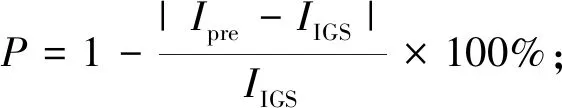
(6)

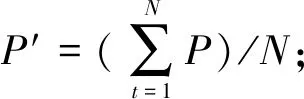
(7)

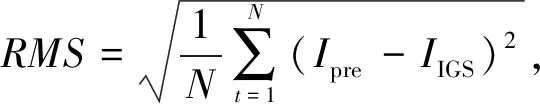
(8)

式中：Ipre為預報值；IIGS為IGS中心發布的觀測值;N為當天觀測的歷元數。

4.2 結果比較與分析

利用3種模型對不同緯度地區在電離層平靜期、 活躍期5天的TEC值進行預報, 得到圖2～4所示的預報結果與實際觀測數據對比圖。 其中，橫坐標表示歷元(每2 h一個歷元), 縱坐標表示TEC值。 無論是在平靜期還是在活躍期, 3種模型對高、 中、 低緯度地區TEC值的預報都能夠很好地反映其變化特征。 但對比發現, 總體上看加法模型預測得到的TEC值與實際值符合情況最好, 乘法模型與ARIMA模型的符合情況稍差。 從太陽活動角度分析, 3種模型在太陽活動平靜期的預報效果均要明顯好于活躍期； 從緯度位置角度分析, 3種模型的預報效果在不同緯度地區會有所差異； 從預報時長角度分析, 3種模型的預報精度均會隨著預報時長的增加而下降。

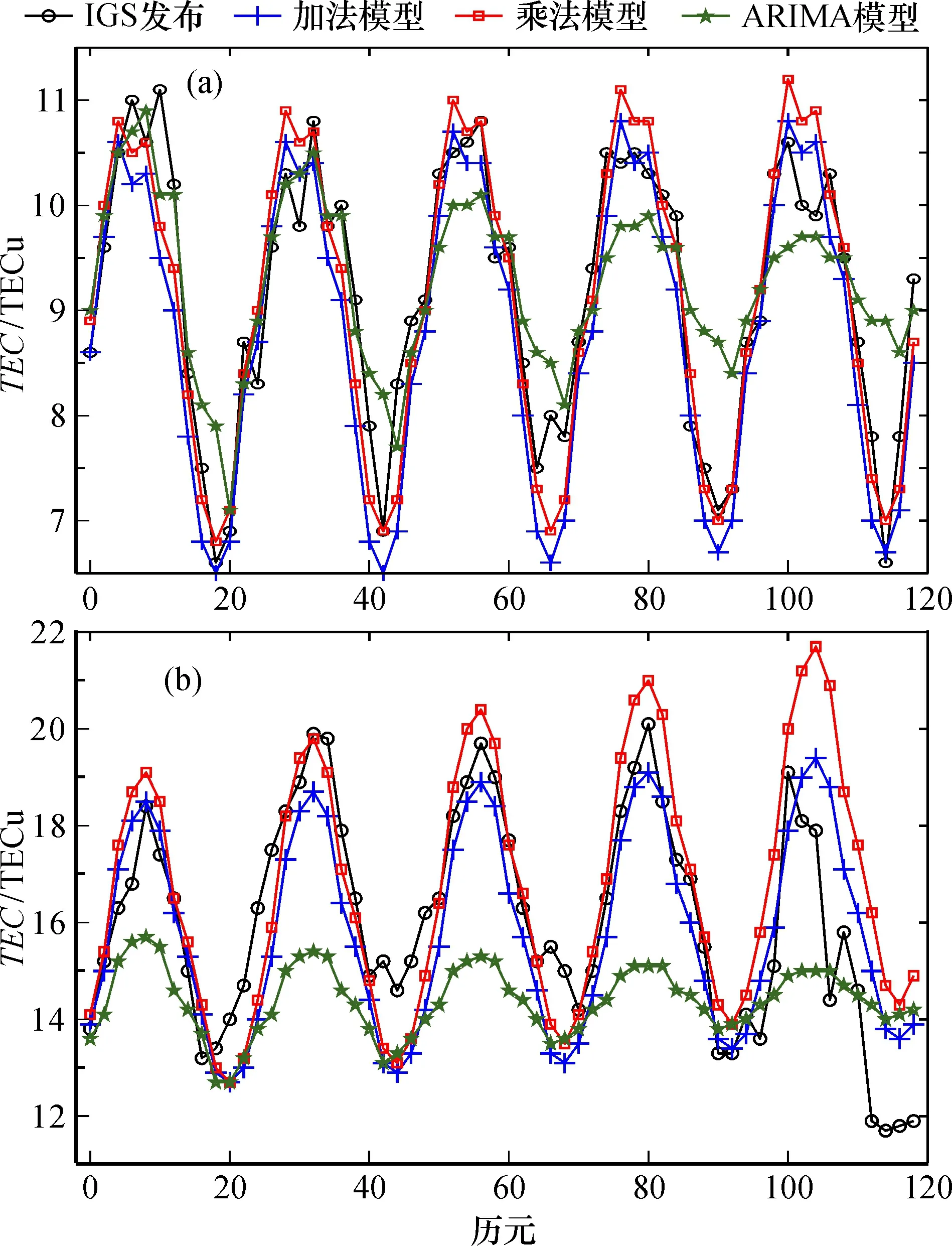
圖2 高緯度地區電離層2009年平靜期(a)、 2011年活躍期(b)TEC值預報結果Fig.2 TEC forecast results at high latitude in ionospheric quiet(a) and active(b) periods in 2009 and 2011

表1和表2分別為電離層平靜期和活躍期3種模型預報值殘差統計。

在平靜期, 加法模型、 乘法模型和ARIMA模型預報值的殘差分別有78%、 57%和56%是在1 TECu之內, 有96%、 76%和82%在2 TECu之內, 說明在平靜期加法模型的預報效果最好, ARIMA模型預報效果次之, 乘法模型預報效果則相對要差些; 而在活躍期, 3個模型預報值殘差在1 TECu之內的分別有23%、 26%、 18%,在3 TECu之內的分別有52%、58%、53%,說明在活躍期乘法模型的預報效果相對來說更為理想,但是并未表現出明顯的優勢;同時可以看出3種模型在平靜期的預報精度明顯高于活躍期。

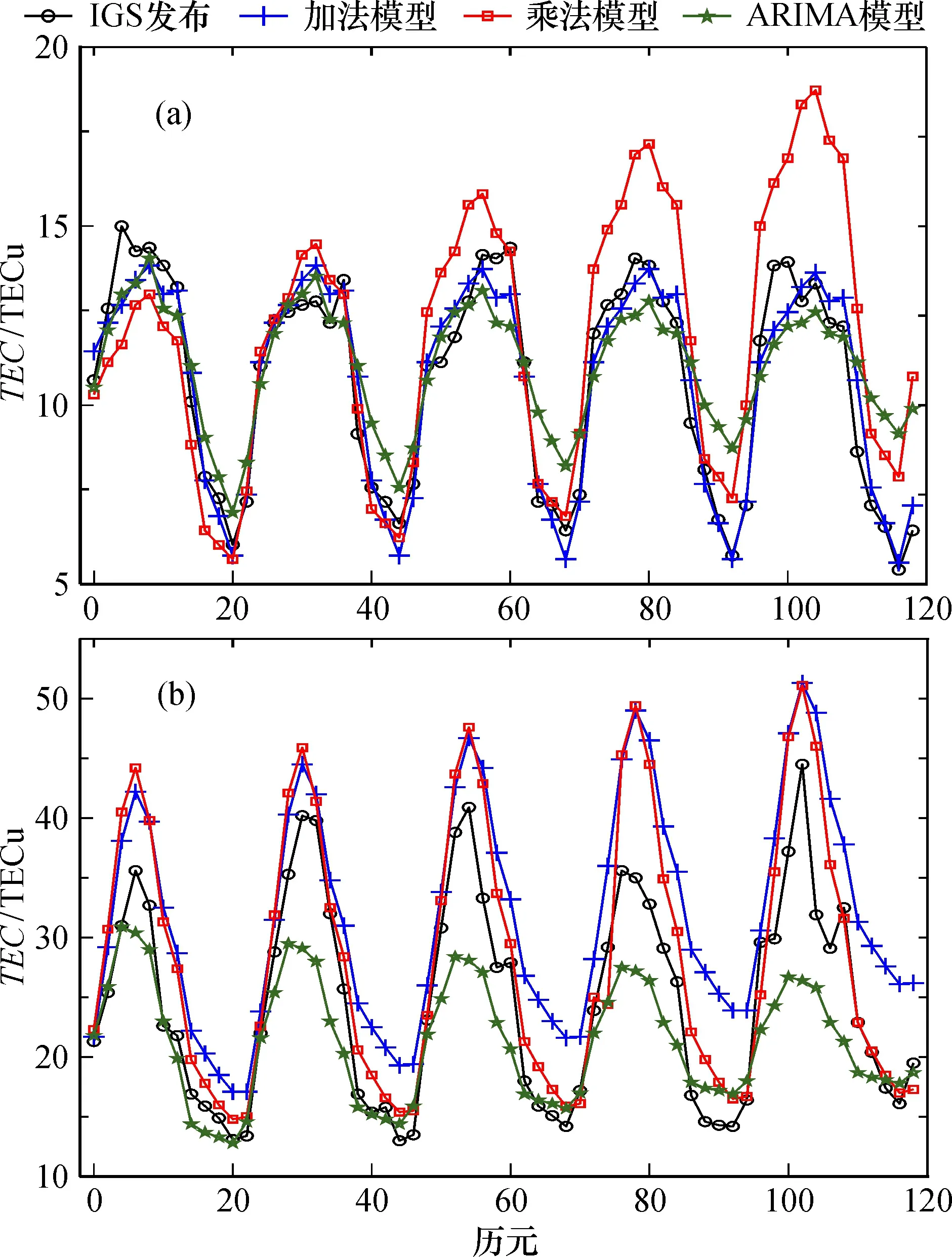
圖3 中緯度地區電離層2009年平靜期(a)、 2011年活躍期(b)TEC值預報結果Fig.3 TEC forecast results at mid-latitude in ionospheric quiet(a)and active(b)periods in 2009 and 2011

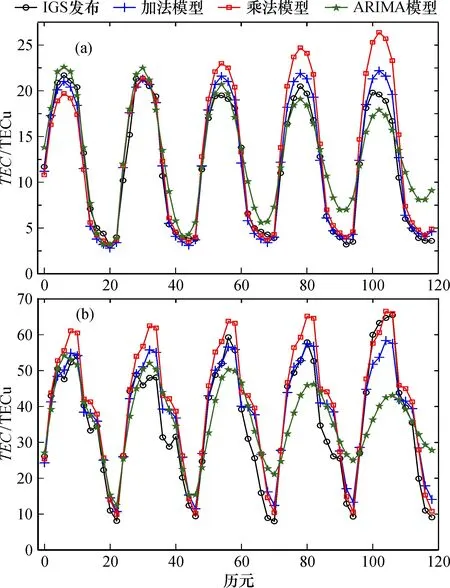
圖4 低緯度地區電離層2009年平靜期(a)、 2011年活躍期(b)TEC值預報結果Fig.4 TEC forecast results at low latitude in ionospheric quiet(a)and active(b)periods in 2009 and 2011

表1 3種模型電離層平靜期預報值殘差(Δ)統計

Table 1 TEC forecast values residual statistics of three models in ionospheric quiet period %

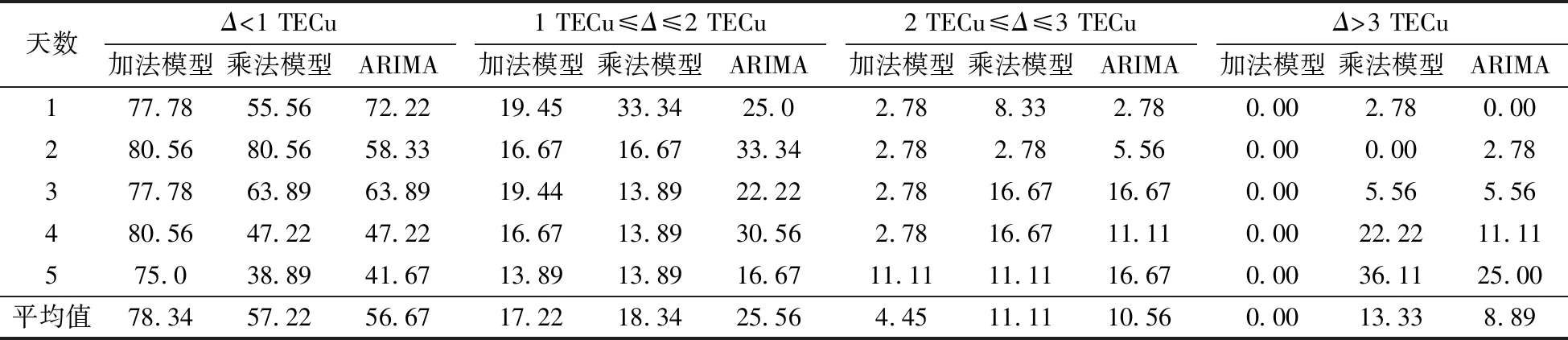
天數Δ<1 TECu加法模型乘法模型ARIMA1 TECu≤Δ≤2 TECu加法模型乘法模型ARIMA2 TECu≤Δ≤3 TECu加法模型乘法模型ARIMAΔ>3 TECu 加法模型乘法模型ARIMA177.7855.5672.2219.4533.3425.02.788.332.780.002.780.00280.5680.5658.3316.6716.6733.342.782.785.560.000.002.78 377.7863.8963.8919.4413.8922.222.7816.6716.670.005.565.56 480.5647.2247.2216.6713.8930.562.7816.6711.110.0022.2211.11 575.038.8941.6713.8913.8916.6711.1111.1116.670.0036.1125.00平均值78.3457.2256.6717.2218.3425.564.4511.1110.560.0013.338.89

表2 3種模型電離層活躍期預報值殘差(Δ)統計

Table 2 TEC forecast values residual statistics of three models in ionospheric active period %

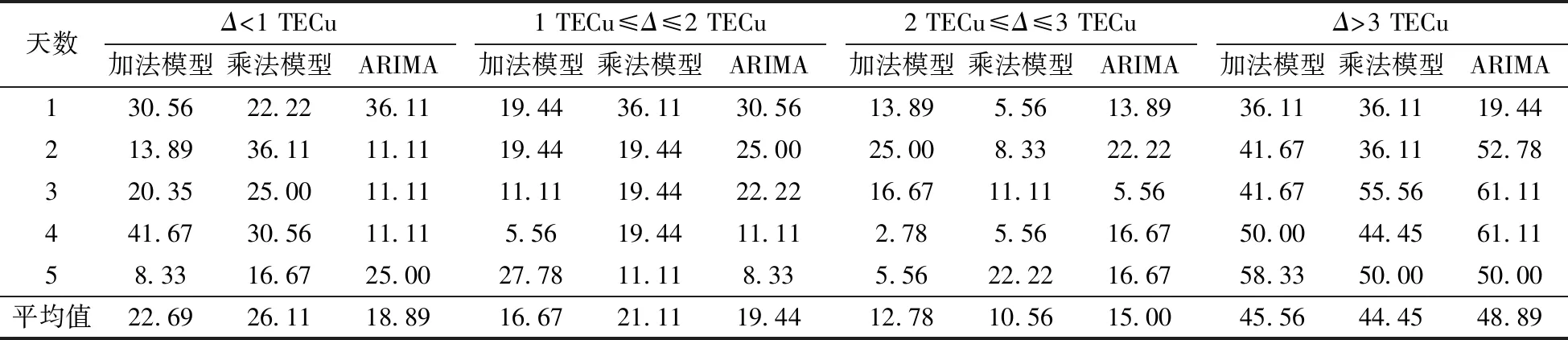
天數Δ<1 TECu加法模型乘法模型ARIMA1 TECu≤Δ≤2 TECu加法模型乘法模型ARIMA2 TECu≤Δ≤3 TECu加法模型乘法模型ARIMAΔ>3 TECu 加法模型乘法模型ARIMA130.5622.2236.1119.4436.1130.5613.895.5613.8936.1136.1119.44 213.8936.1111.1119.4419.4425.0025.008.3322.2241.6736.1152.78 320.3525.0011.1111.1119.4422.2216.6711.115.5641.6755.5661.11 441.6730.5611.115.5619.4411.112.785.5616.6750.0044.4561.11 58.3316.6725.0027.7811.118.335.5622.2216.6758.3350.0050.00 平均值22.6926.1118.8916.6721.1119.4412.7810.5615.0045.5644.4548.89

分析平靜期3個模型的預報殘差會發現, 加法模型在前4天預報表現較為平穩, 均有約96%的預報殘差能保持在2 TECu之內, 而到了第5天則下降至89%; 乘法模型在前兩天均有89%的預報殘差保持在2 TECu之內, 到了第3天則下降至78%, 第4天進一步降至61%;ARIMA模型在前兩天有92%的預報殘差保持在2 TECu之內,第3、4天降至約78%,第5天進一步降至58%。以上分析說明,在平靜期3種模型的預報精度會隨著預報時長的增加而下降;加法模型能夠維持5天以上的精確預報,而乘法模型和ARIMA模型只有3天左右。在活躍期,3種模型的預報精度隨著預報時長的增加波動較大,但是從總體上看依舊呈下降趨勢。

表3和表4分別是平靜期和活躍期3種模型預報值相對精度統計。

表3 3種模型電離層平靜期年預報值日均相對精度(P′)

Table 3 Daily relative accuracy of TEC forecast values for three models in ionospheric quiet period

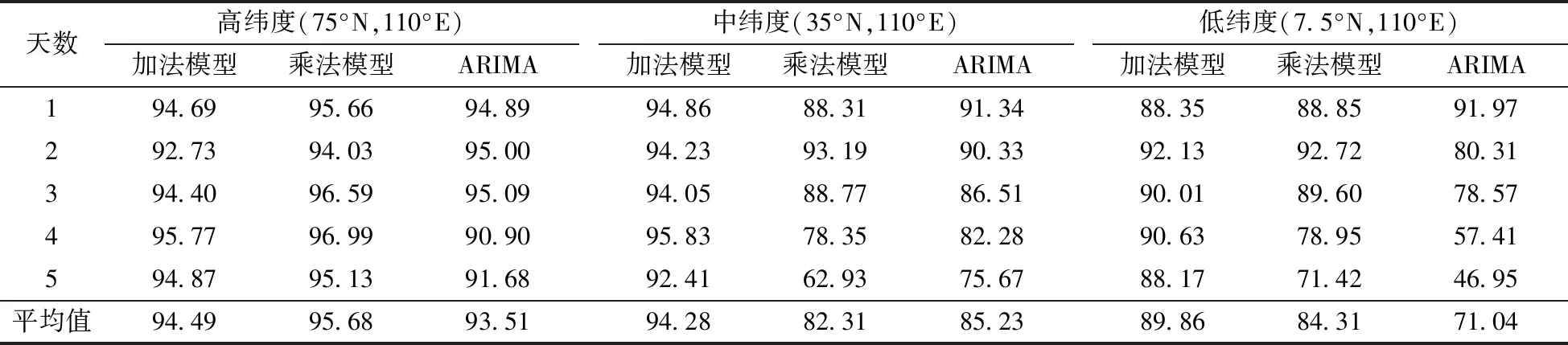
天數高緯度(75°N,110°E)加法模型乘法模型ARIMA中緯度(35°N,110°E)加法模型乘法模型ARIMA低緯度(7.5°N,110°E) 加法模型乘法模型ARIMA194.6995.6694.8994.8688.3191.3488.3588.8591.97 292.7394.0395.0094.2393.1990.3392.1392.7280.31 394.4096.5995.0994.0588.7786.5190.0189.6078.57 495.7796.9990.9095.8378.3582.2890.6378.9557.41 594.8795.1391.6892.4162.9375.6788.1771.4246.95 平均值94.4995.6893.5194.2882.3185.2389.8684.3171.04

表4 3種模型電離層活躍期年預報值日均相對精度P′

Table 4 Daily relative accuracy of TEC forecast values for three models in ionospheric active period %

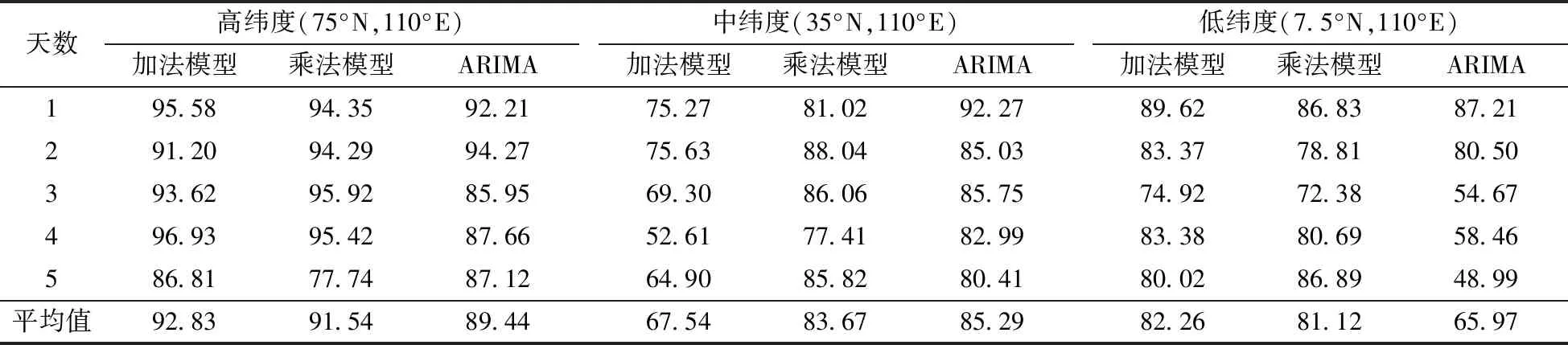
天數高緯度(75°N,110°E)加法模型乘法模型ARIMA中緯度(35°N,110°E)加法模型乘法模型ARIMA低緯度(7.5°N,110°E) 加法模型乘法模型ARIMA195.5894.3592.2175.2781.0292.2789.6286.8387.21 291.2094.2994.2775.6388.0485.0383.3778.8180.50 393.6295.9285.9569.3086.0685.7574.9272.3854.67 496.9395.4287.6652.6177.4182.9983.3880.6958.46 586.8177.7487.1264.9085.8280.4180.0286.8948.99 平均值92.8391.5489.4467.5483.6785.2982.2681.1265.97

在平靜期,3種模型預報值的相對精度均隨著緯度的降低而下降:就高緯度地區而言,3種模型預報值的相對精度大致相當,平均值均為94%左右;就中緯度地區而言,加法模型的預報精度最高,相對精度均值為94%,乘法模型和ARIMA模型的預報精度相當,相對精度均值在84%左右;就低緯度地區而言,加法模型的預報精度最高,相對精度均值將近達到90%,乘法模型次之,相對精度均值為84%,ARIMA模型較差,相對精度均值僅為71%。而在活躍期,3種模型預報值相對精度在高緯度地區大致相當,均在90%左右;在中緯度地區,加法模型的預報精度較差,相對精度均值約為68%,乘法模型和ARIAM模型的預報精度更好,相對精度均值為84%左右,這與平靜期所呈現規律有所不同,原因是活躍期電子含量變化較大,對建立模型帶來了一定的偏差;而在低緯度地區,加法模型和乘法模型的預報精度較好,相對精度均值為81%左右,ARIMA模型的預報精度較差,相對精度均值僅為66%;總體上看,在活躍期3種模型的預報精度也是從高緯度向低緯度呈遞減趨勢。另外,3種模型預報值相對精度也是隨著預報時長的增加而成遞減趨勢。

表5為3種模型預報值均方差統計。在平靜期, 3種模型5天預報值均方差的平均值比在活躍期要小, 說明在平靜期的預報精度更高, 與表1和表2所得結論相同。 在平靜期，3種模型5天預報值均方差的平均值隨著緯度的降低而增大, 預報精度下降; 而在活躍期，總體上也呈現相同趨勢, 但表現出一定的波動,這同樣是因為在活躍期電子含量變化幅度較大,使得原始時間序列較不平穩,雖然經過平穩化處理,但還是給模型的建立帶來了一定的誤差。 分析預報時長對預報精度的影響,對3種模型每天各緯度的預報值均方差求平均值, 在平靜期, 加法模型從第1天的0.88增加到第5天的1.05;乘法模型從第1天的1.21增加到第5天的2.88;ARIMA模型從第1天的0.84增加到第5天的2.19。在活躍期,加法模型從第1天的3.05增加到第5天的5.86；乘法模型從第1天的3.84增加到第5天的4.47；ARIMA模型從第1天的2.31增加到第5天的8.72。3種模型的預報精度均隨著預報時長的增加呈遞減趨勢,與從表1和表2所得結論相同。

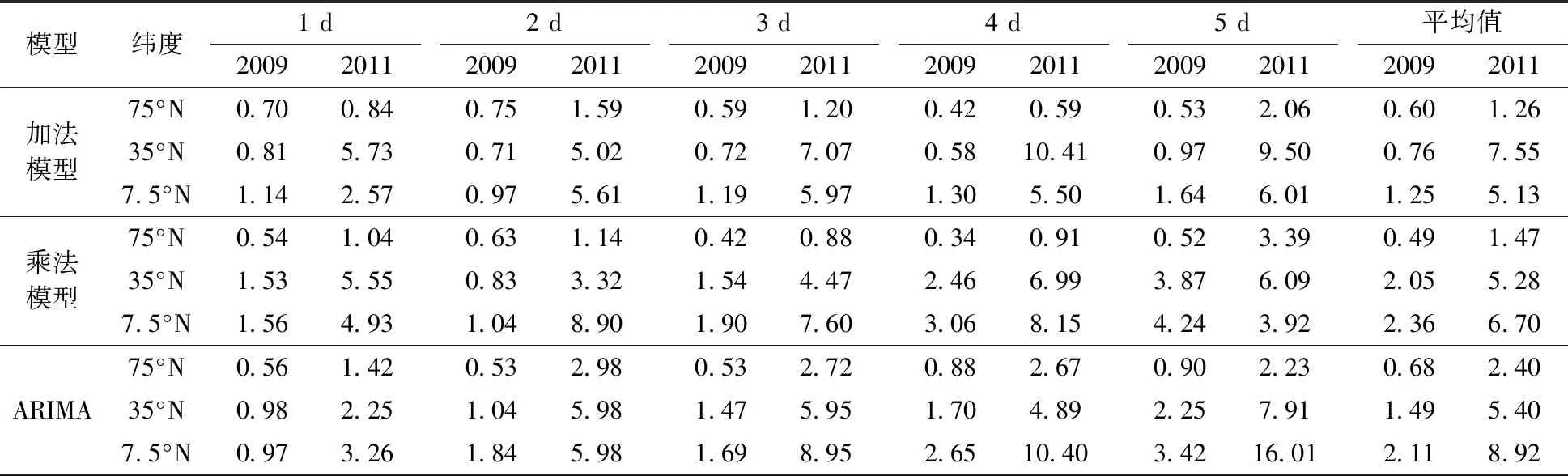
表5 3種模型預報值均方差RMS統計Table 5 RMS of forecast values for three models in active and quiet periods

5 結 論

本文分別采用Holt-Winters加法模型、Holt-Winters乘法模型和ARIMA模型,利用IGS中心發布的不同緯度地區不同太陽活動情況下的電離層TEC樣本數據進行5天的預報,并且將預報結果與IGS中心提供的實測數據進行對比分析,得到如下結論:

(1)3種模型的預報精度會隨著緯度的降低和預報時長的增加而下降;相較于太陽活動活躍期,3種模型在太陽活動平靜期的預報精度更高。

(2)太陽活動平靜期:在高緯度地區,3種模型的預報精度相當;在中緯度和低緯度地區,Holt-Winters加法模型的預報精度要優于另外兩種模型。

(3)太陽活動活躍期:在高緯度地區,3種模型的預報精度相當;在中緯度地區,Holt-Winters乘法模型和ARIMA模型預報精度相當,優于Holt-Winters加法模型;在低緯度地區,Holt-Winters加法模型和Holt-Winters乘法模型的預報精度相當,要優于ARIAM模型。

(4)Holt-Winters加法模型能夠維持5天以上較為精準的預報,而乘法模型和ARIMA模型只有3天左右。