特殊可逆矩陣的一個(gè)性質(zhì)

2019-02-12 03:12:46饒維亞關(guān)麗紅

長春大學(xué)學(xué)報(bào) 2019年12期

饒維亞，關(guān)麗紅

(長春大學(xué) 理學(xué)院，長春 130022)

n級(jí)矩陣A可逆的充分必要條件是A可寫為若干n級(jí)初等矩陣的乘積[1]，即：

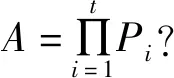
1 初等矩陣及其行列式的值

采用文獻(xiàn)[1]中的記號(hào)，其中E表示單位矩陣。

第一類初等矩陣P(i,j)：表示交換E的第i行與第j行所得到的矩陣；

第二類初等矩陣P(i(c))：表示用非零常數(shù)c乘以E的第i行所得到的矩陣；

第三類初等矩陣P(i,j(k))：表示E的第j行的k倍加至第i行所得到的矩陣。

顯然：P(i,j)-1=P(i,j)，P(i(c))-1=P(i(c-1))，P(i,j(k))-1=P(i,j(-k))，

且有: detP(i,j)=-1，detP(i(c))=c，detP(i,j(k))=1.

從而有:

引理1 三類初等矩陣中，僅第三類初等矩陣，它的行列式的值等于1。

2 3級(jí)矩陣情形

引理2 任意一個(gè)3級(jí)第一類初等矩陣，都等于一個(gè)非零常數(shù)與若干第三類初等矩陣的乘積。

證明：不失一般性，我們討論3級(jí)初等矩陣P(1,2)，對它進(jìn)行一系列的初等變換

記ai=-1，則det(aiQ)=1，對aiQ仿上變換，有:

可知：

E=aiP(2,3(1))P(3,2(-1))P(2,3(1))P(3,2(-1))P(2,3(1))P(3,2(-1))，

P(1,2(-1))P(2,1(1))P(1,2(-1))P(1,2)。

從而：

P(1,2)=a-1iP(1,2(1))P(2,1(-1))P(1,2(1))P(3,2(1))P(2,3(-1))，

P(3,2(1))P(2,3(-1))P(3,2(1))P(2,3(-1))。

即第一類初等矩陣P(1,2)可以寫成非零常數(shù)ai與若干第三類初等矩陣的乘積。

引理 3 任意一個(gè)3級(jí)第二類初等矩陣，都等于一個(gè)非零常數(shù)與若干第三類初等矩陣的乘積。

證明：首先討論2級(jí)矩陣的情形。

設(shè)a是非零常數(shù)，不失一般性，討論2級(jí)矩陣P(1(a))，其中a≠1。

對于復(fù)數(shù)a，總可以寫成a=c2的形式，記ai=c-1，則：

對它進(jìn)行一系列初等變換：

可知：

E=aiP(1,2(c-1-c-2))P(2,1(-c))P(1,2(c-1-1))P(2,1(1))P(1(a))。

于是，2級(jí)第二類初等矩陣P(1(a))可以寫成非零常數(shù)ai與若干第三類初等矩陣的乘積。

再討論3級(jí)的情形。仍不失一般性，對3級(jí)矩陣P(1(a))進(jìn)行討論，其中a≠1。

設(shè)a=c3，記ai=c-1，則

進(jìn)行初等變換有：

對最后一個(gè)矩陣的第二行和第三行，再按照2級(jí)的變換方式，進(jìn)行一系列初等變換，可得E=aiP(2,3(c-1-c-2))P(3,2(-c))P(2,3(c-1-1))P(3,2(1))P(1,2(c-2-c-4))，

P(2,1(-c2))P(1,2(c-2-1))P(2,1(1))P(1(a))。

于是，3級(jí)第二類初等矩陣P(1(a))可以寫成非零常數(shù)ai與若干第三類初等矩陣的乘積。

定理1 一個(gè)行列式的值為1的3級(jí)矩陣，可以寫成若干個(gè)行列式的值為1的初等矩陣的乘積。

證明：由引理2、引理3知，任一第一、二類初等矩陣都可寫成非零常數(shù)與若干第三類初等矩陣的乘積。又已知3級(jí)矩陣的行列式的值為1，由引理1知：所有第三類初等矩陣的行列式的值都等于1，故所有常數(shù)的乘積必為1。從而3級(jí)行列式的值為1的矩陣可以寫成若干個(gè)行列式的值為1的初等矩陣的乘積。