干濕循環作用下膨脹巖崩解的粒度熵特征
張宗堂, 高文華, 唐驍宇, 張巨峰, 韓 森
(1.湖南科技大學 資源環境與安全工程學院, 湖南 湘潭 411201;2.湖南科技大學 巖土工程穩定控制與健康監測湖南省重點實驗室, 湖南 湘潭 411201)
1 研究背景
膨脹巖能在水環境下發生物理化學反應,從而產生膨脹與崩解[1-3]。且膨脹巖中含有一定的膨脹性黏土礦物,其崩解性比其他巖石更加明顯。由于膨脹巖在我國分布廣泛,所以被大量應用于工程建設當中,然而,隨著工程建設的不斷完善,膨脹巖在交通、水利、礦山等領域的遇水崩解問題日益突出[2-3]。故對膨脹巖在干濕循環作用下崩解特性的研究具有重要的意義。
Clausius[4]提出了“熵”的概念,并用“熵”來描述系統的混亂程度。Shannon[5]將統計熵用于信息理論中,運用其描述系統信息的不確定性。Jaynes[6]提出最大信息熵原理,用以確定各種系統隨機變量的概率分布函數,使其在眾多領域得到了廣泛應用。L?rincz[7]提出粒度熵,并采用基礎熵和熵增量來量化巖土顆粒級配曲線特征的紊亂程度。田海等[8]依據貝殼砂試樣試驗前后粒徑分布資料,在統計熵概念基礎上提出顆粒破碎粒度熵模型,認為貝殼砂顆粒破碎粒度熵參數能較好地描述其顆粒破碎行為。曾志雄等[2]根據干濕循環后膨脹巖的粒徑分布,引入標準基礎熵來表征膨脹巖的崩解特性,指出可以將標準基礎熵作為巖石崩解的量化指標,并通過與崩解比的對比分析驗證了該方法的合理性。
目前,已有不少對于巖石崩解特性的研究,其中,申培武等[9]、曾志雄等[2]、梁冰等[10]、梁越等[11]、趙吉霞等[12],田巍巍等[13]均對巖石在干濕循環作用下的崩解情況展開研究,但是對于膨脹巖在不同干燥溫度、外界擾動、不同初始單塊質量情況下崩解特性的研究鮮見報道。因此,本文基于粒度熵的概念,對干濕循環作用下膨脹巖在不同干燥溫度、外界擾動、不同初始單塊質量情況下崩解的粒度熵特征展開研究。
2 膨脹巖崩解的粒度熵表征
粒徑級配曲線反映了固體顆粒的粒徑分布狀況,但由于其含有較多數據而缺少單一量化指標,故難以對不同曲線顆粒的粒度分布情況進行整體比較。因此,Imre等[14]、L?rincz[15]提出粒度熵用于量化顆粒級配曲線,表征巖土顆粒級配的紊亂程度。由此可見,可以采用粒度熵來描述巖石崩解后顆粒的粒徑分布狀況,并以此度量巖石的崩解破碎程度。
2.1 信息熵原理
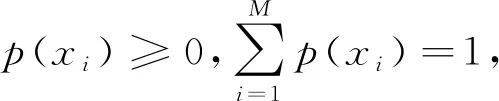
(1)
2.2 粒度熵的概念
L?rincz定義了“截斷”的概念[2,14-15],第i個截斷(即第i個粒組)的顆粒粒徑d的范圍:
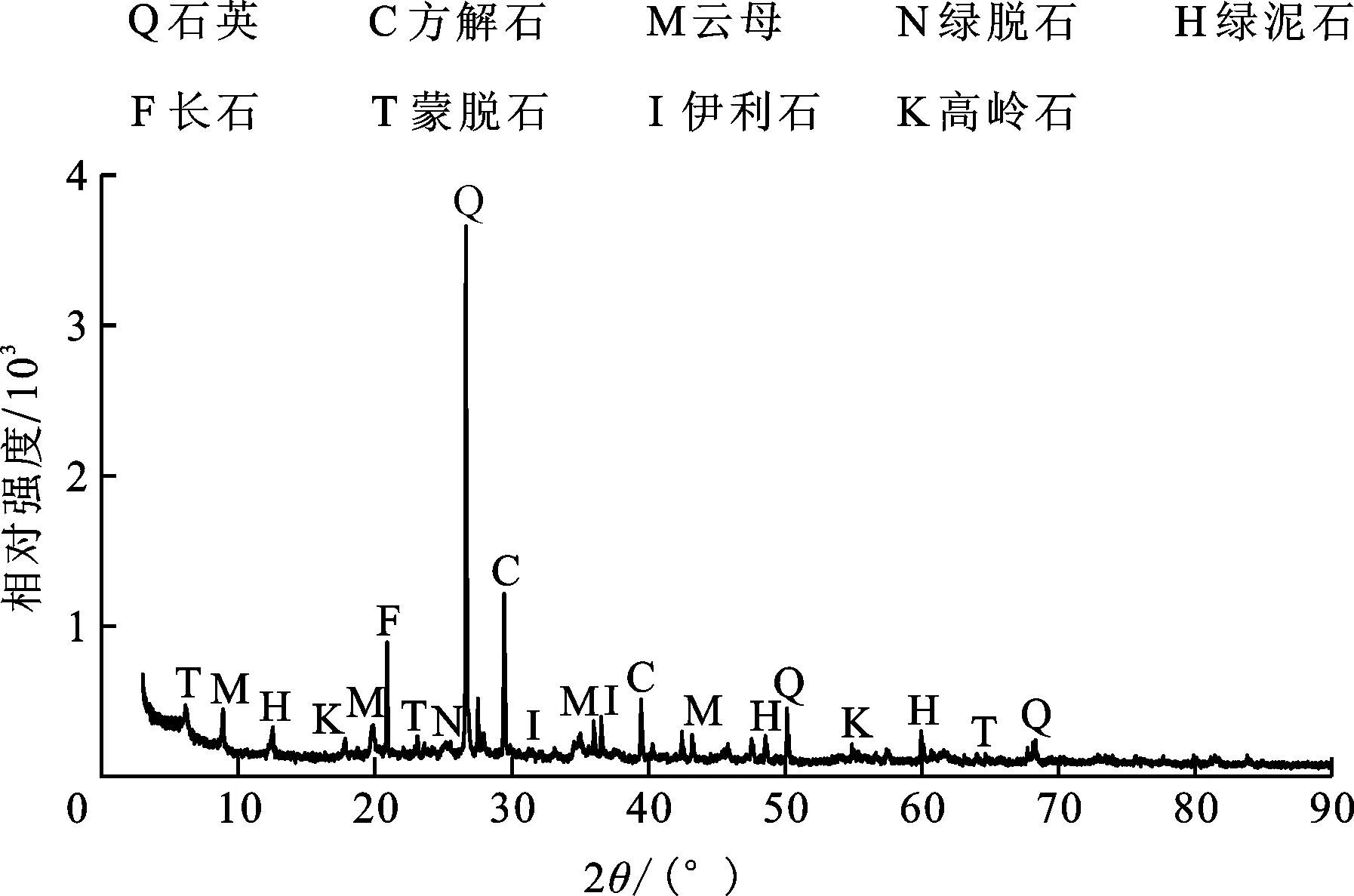
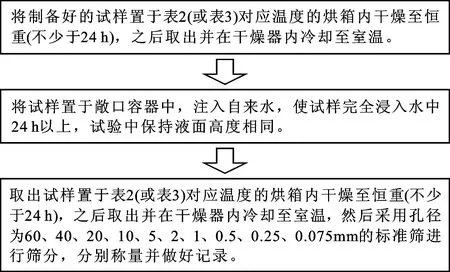
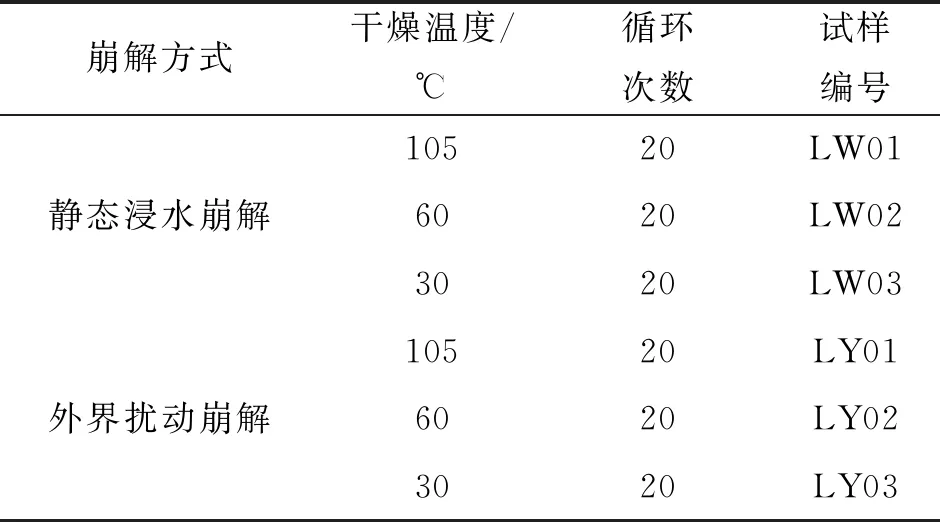
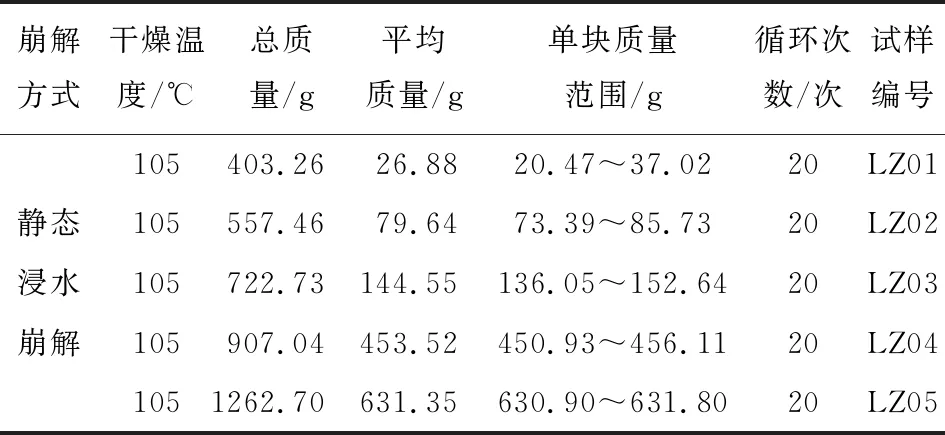
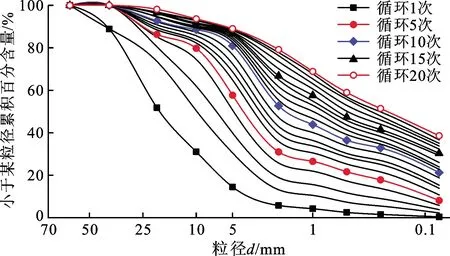
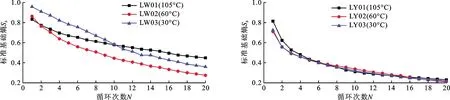
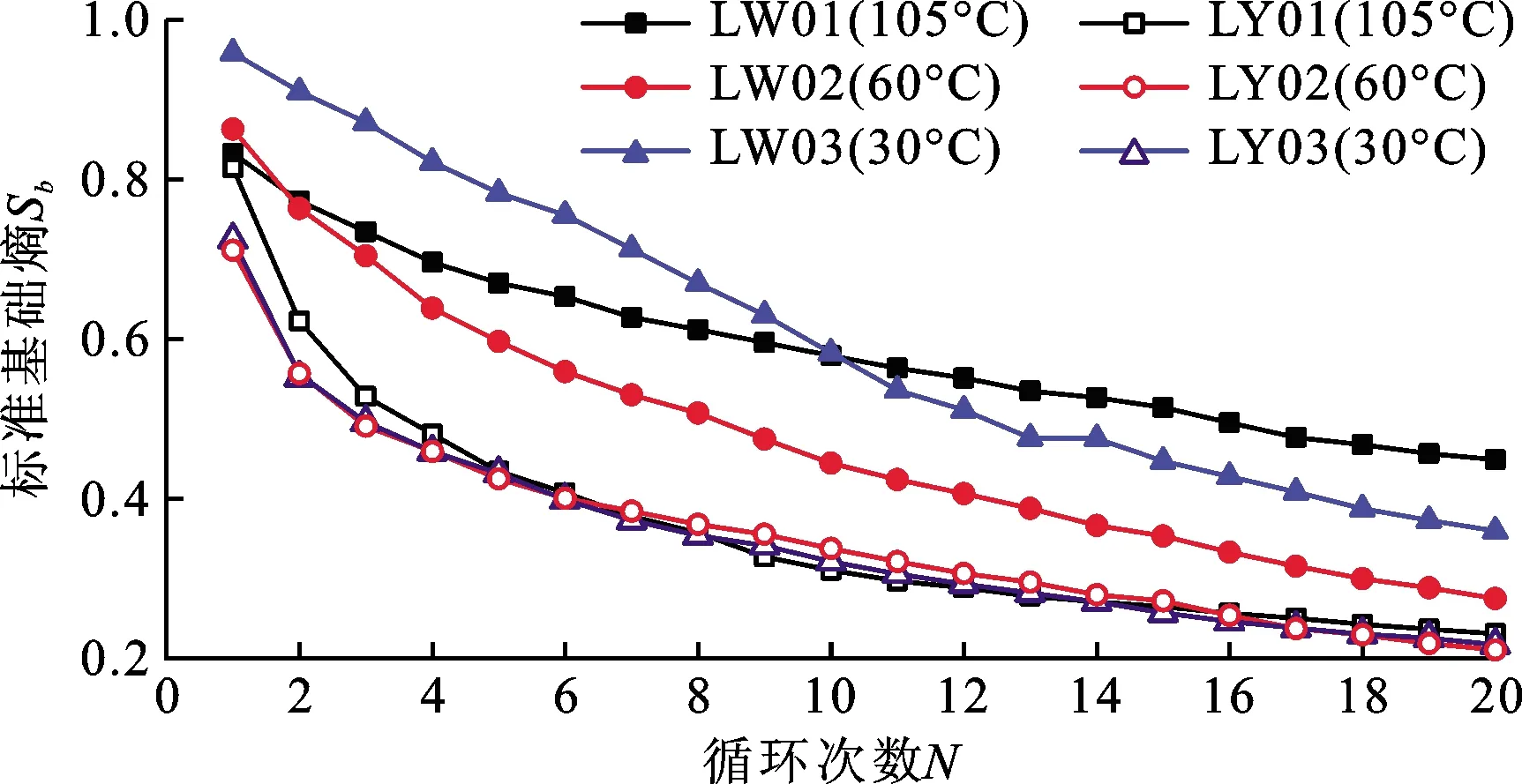
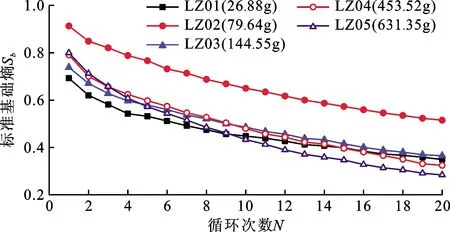
Ri-1 (2) 式中:m為截斷數目,即粒組劃分數量;i為粒組劃分的序號;Ri為截斷尺寸序列,即第i個篩孔的孔徑,mm。 設在第i個粒組內的顆粒含量為Mi,則各粒組的顆粒含量之和滿足: (3) 假設最小顆粒以最小篩孔直徑dmin的長度在各粒組內均勻分布,則在第i個粒組內包含的最小顆粒的數量為: (4) 各粒組被劃分成j份,每個j內的相對頻度pj均相等: (5) 考慮到各粒組被劃分為j份,且共劃分了m個粒組,將公式(5)代入公式(1),計算可得粒度熵S為: (6) 為便于在同一標準下研究及消除最小篩孔直徑的影響,采用文獻[2]、[14-15]的計算方法將公式(6)寫成基礎熵(S0)與熵增量(ΔS)并進行標準化,則: S=S0+ΔS (7) (8) (9) 依據文獻[2]定義第i個粒組的特征熵為: S0i=log2Ci (10) 標準基礎熵為: (11) 由公式(4)、(10)、(11)可得: (12) 標準熵增量為: (13) 式中:ΔRi為第i個粒組的寬度,mm;ΔR1為粒組寬度最小值,mm;ΔRN為粒組寬度最大值,mm。 標準基礎熵體現了粒組寬度差異的影響:大顆粒含量越多,其值越大,反之越小[14-15]。由此可知,在巖石崩解過程中,其標準基礎熵越小,則其崩解物的小顆粒含量越多,其崩解速率越快。 試驗樣品為湖南省株洲地區的紅砂巖,依據《巖石物理力學性質試驗規程(DZ/T 0276.9-2015)》[17],基本物理力學性質如表1。對膨脹巖進行X射線衍射試驗,獲取了其礦物成分,其中,石英40.85%,方解石20.47%,長石12.84%,云母8.41%,高嶺石6.96%,綠泥石5.24%,伊利石2.52%,綠脫石1.16%,蒙脫石0.81%,其他0.74%,圖1為膨脹巖試樣XRD衍射圖譜,由此可知,其主要礦物成分為石英,且含有一定的膨脹性黏土礦物。依據朱訓國等[18]對膨脹巖的判別標準可知,該紅砂巖為微膨脹巖。 表1 膨脹巖試樣基本物理力學性質 圖1 膨脹巖試樣XRD衍射圖譜 崩解試驗采用靜態崩解與擾動崩解兩種崩解方式,其中靜態崩解試驗流程如圖2所示。 圖2 靜態崩解試驗流程圖 擾動崩解試驗采用濟南海威爾儀器有限責任公司生產的HNB-1巖石耐崩解試驗儀(如圖3),試驗步驟為:將圖2中第2步變為:將試樣置于耐崩解性試驗儀的篩桶中,在水槽中注入自來水至設計水位,打開開關使篩筒以20 r/min的轉速轉動10 min,其余步驟與上述靜態崩解試驗完全相同。 為了研究干濕循環作用下干燥溫度不同時膨脹巖崩解的粒度熵特征,開展了干燥溫度不同情況下的靜態與擾動崩解試驗,試驗方案見表2。 圖3 HNB-1巖石耐崩解試驗儀 表2 靜態與擾動崩解試驗方案設計一覽表 實際環境中并非僅存在單一塊度的巖石,而是由大小不等的多塊度巖石組成的。為了研究干濕循環作用下初始單塊質量不同時膨脹巖崩解的粒度熵特征,開展了初始單塊質量不同情況下的靜態崩解試驗,試驗方案見表3,干燥溫度為105℃。 表3 不同初始單塊巖石質量靜態崩解試驗方案設計一覽表 由于篇幅所限,此處僅取其中一組試驗結果(LW02)進行顆粒級配分析。圖4為膨脹巖崩解顆粒級配曲線,為便于識別干濕循環作用下膨脹巖崩解顆粒級配曲線的變化情況,圖4僅標記出干濕循環1、5、10、15、20次的級配曲線,其余曲線隨循環次數的增加依次分布在各標記曲線之間。由圖4可知,級配曲線的形狀整體呈反S形,且隨著循環次數的增加:(1)各曲線逐漸靠近,最終趨于重合,這與崩解情況隨著循環次數的增加逐漸趨于相對穩定是一致的;(2)級配曲線反S形上凸的部分愈加凸出,而下凹的部分逐漸減弱;(3)崩解顆粒的級配曲線逐漸向粒徑減小的方向移動。 圖4 不同干濕循環次數膨脹巖試樣(LW02)崩解顆粒級配曲線 為了研究干燥溫度不同情況下膨脹巖崩解的粒度熵特征,采用30℃模擬室溫情況下膨脹巖的干燥溫度,采用60℃模擬室外高溫情況下膨脹巖所能達到的干燥溫度,105℃為試驗規程[17]所要求的干燥溫度。圖5為靜態崩解情況下巖樣首次浸水與20次循環后殘留樣圖,圖6為擾動崩解情況下巖樣與20次循環后殘留樣圖。 由公式(12)求得上述6組試樣的標準基礎熵,圖7為靜態崩解的Sb-N關系曲線,圖8為擾動崩解的Sb-N關系曲線。由圖7可知,當干燥溫度不同時,靜態崩解情況下的各標準基礎熵差距明顯;在循環次數相同條件下,60℃干燥溫度下得到的標準基礎熵最小。由此可知,靜態崩解情況下,干燥溫度對膨脹巖崩解的標準基礎熵影響很大,相對于105℃、30℃的干燥溫度,60℃干燥溫度下的標準基礎熵最小,最有利于膨脹巖的崩解,且循環次數越多。由圖8可知,擾動崩解情況下對應曲線之間的間距非常小,標準基礎熵非常接近,故與靜態崩解情況下膨脹巖崩解的標準基礎熵相比,其崩解情況幾乎不受干燥溫度的影響。 產生上述現象的原因是,靜態崩解情況下,殘留樣中的水分在30℃的干燥溫度下只有重力水流失,其余的大部分滯留于試樣內部無法逸出,在干濕循環作用下,滯留于試樣內部的水分變化很小,故其對巖樣造成的影響較小;殘留樣中的全部水分能夠在105℃的干燥溫度下迅速汽化為水蒸氣而散失,水熱共同作用于試樣的時間最短,每次循環過程中水分的置換最徹底;在60℃的干燥溫度下,巖樣中非自由水只能失去一部分而無法全部失去,在干濕循環過程中,水分的置換比較明顯,且試樣在水熱共同作用下的時間較長,對試樣孔裂隙的擴展影響較大,故60℃的干燥溫度對試樣崩解的標準基礎熵影響最大。由此可見,水熱共同作用對膨脹巖崩解標準基礎熵的影響大于僅有水或熱單獨存在的情況。擾動崩解情況下,外界擾動對膨脹巖崩解標準基礎熵的影響遠大于干燥溫度的影響。采用崩解破碎后的膨脹巖作為工程填料時,可以選擇在夏季高溫季節對膨脹巖進行反復的浸水處理,因為在夏季高溫季節巖體的溫度可能達到60℃,而此溫度下更有利于膨脹巖的崩解破碎,能以比較經濟的手段使得膨脹巖較快速的崩解破碎至工程需要的程度。 為了研究外界擾動情況下膨脹巖崩解的粒度熵特征,將上述4.2節中靜態與擾動崩解情況下的標準基礎熵繪制到同一幅圖中,圖9為靜態(LW01~LW03)與擾動(LY01~LY03)崩解的標準基礎熵與循環次數的關系曲線,由圖9可知,擾動情況下膨脹巖崩解的標準基礎熵明顯小于靜態崩解情況下,則擾動崩解的速率明顯快于靜態崩解;而當循環次數較多時,60℃干燥溫度下靜態崩解的標準基礎熵與擾動崩解比較接近,則60℃干燥溫度下的靜態崩解速率接近擾動崩解。 圖5靜態崩解情況下巖樣首次浸水與20次循環后殘留樣圖 圖6擾動崩解情況下巖樣與20次循環后殘留樣圖 圖7靜態崩解的Sb-N曲線 圖8擾動崩解的Sb-N曲線 產生這種現象的原因主要為:(1)外界擾動情況下巖樣的崩解試驗采用HNB-1巖石耐崩解試驗儀進行,位于轉動篩桶中的巖樣會受到水槽中靜態水的相對沖刷作用,水的相對動力沖刷加速了膨脹巖的崩解;(2)相對的動水作用加速了膨脹巖中部分黏土礦物與水的化學反應,且相對的動水作用使得膨脹巖顆粒間的黏結物在溶于水的瞬間被水帶走,導致膨脹巖內部的孔裂隙加速發育;(3)轉動篩桶與顆粒間以及不同顆粒間的機械碰撞加速了膨脹巖的崩解。 圖9 試樣靜態與擾動崩解的Sb-N對比圖 此研究對于工程應用具有一定的實際意義:在需要膨脹巖快速崩解為工程所需粒徑的情況下,或者外界干燥溫度沒有接近60℃時,可以選擇適當施加一定的外力擾動使干濕循環作用下的膨脹巖快速崩解。靜態崩解情況下,干燥溫度為60℃左右時,只要干濕循環次數足夠多,其崩解程度不亞于外界擾動崩解,但其需要的時間較長;而外界擾動情況下,崩解程度幾乎不受干燥溫度的影響,可以在不同季節選擇施工,其崩解速率亦比靜態崩解情況下迅速,但其需要施加外力擾動,則需要額外施加一定的機械能,沒有靜態浸水情況下經濟。 試驗方法采用靜態崩解試驗,試驗方案見表3。為避免含水率不同對膨脹巖崩解的影響,本試驗采用105℃的干燥溫度。圖10為巖樣首次浸水圖,圖11為巖樣干濕循環20次后殘留樣圖。由公式(12)求得各組試樣的標準基礎熵,圖12為初始單塊質量不同情況下Sb-N關系曲線,由圖12可知,初始單塊質量不同對膨脹巖崩解的標準基礎熵存在一定的影響:初始單塊質量越大,其標準基礎熵越小(LZ01除外);且隨著循環次數的增加,其標準基礎熵不斷減小。 產生這種現象的原因主要為:膨脹巖初始單塊質量越大,則其由自然環境導致的內部缺陷越多,崩解后得到的標準基礎熵越小。 依據《巖石物理力學性質試驗規程DZ/T0276.9-2015》,求解得到各組試樣的耐崩解性指數IdN,建立耐崩解性指數與標準基礎熵的回歸分析,由于篇幅所限,此處僅給出LW02試樣的回歸分析過程,如圖13所示。由圖13可知,標準基礎熵度量崩解的方法與規程要求的方法具有較好的相關性,從而驗證了該方法的可行性。 圖10 巖樣首次浸水圖 圖11 巖樣干濕循環20次后殘留樣圖 圖12 不同初始單塊巖樣質量的Sb-N曲線 圖13 標準基礎熵與規程方法對比(LW02) 標準基礎熵為反映崩解物級配曲線的量化指標,能夠考慮到巖石崩解之后各粒組巖石顆粒的整體分布狀況,而耐崩解性指數僅反映出巖石崩解之后兩個粒組(大于2 mm與小于2 mm)的分布狀況。因此,相對于耐崩解性指數,標準基礎熵更適用于評價巖石的崩解情況。 (1)干燥溫度對膨脹巖崩解的標準基礎熵存在一定的影響。在靜態崩解方式下,相對于105、30℃干燥溫度而言,60℃干燥溫度下的標準基礎熵最小,表明60℃的干燥溫度更有利于膨脹巖的崩解。而在外界擾動崩解方式下,膨脹巖的崩解程度幾乎不受干燥溫度的影響。 (2)外界擾動對膨脹巖崩解的標準基礎熵存在顯著影響。在干燥溫度、初始單塊質量等因素不變的情況下, 外界擾動情況下膨脹巖的標準基礎熵均小于靜態崩解情況下的各參數值。 (3)初始單塊質量不同對膨脹巖崩解的標準基礎熵存在一定的影響。初始單塊質量越大,其標準基礎熵越小,崩解速率越快;且隨著循環次數的不斷增加,其標準基礎熵不斷減小。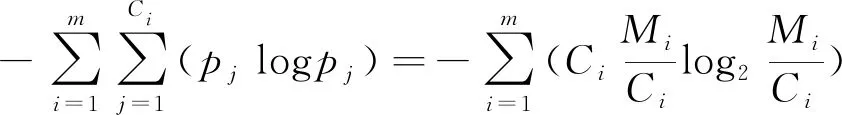
2.3 粒度熵的標準化
3 試樣與試驗方法
3.1 試樣基本性質

3.2 試驗方法

4 試驗結果與分析
4.1 干濕循環作用下膨脹巖崩解顆粒級配曲線分析
4.2 干燥溫度不同情況下膨脹巖崩解的粒度熵特征
4.3 外界擾動情況下膨脹巖崩解的粒度熵特征

4.4 初始單塊質量不同時膨脹巖崩解的粒度熵特征
4.5 標準基礎熵與規程方法對比分析



5 結 論

