一種空氣沖擊波超壓隨密度變化的計算模型

甘朝虹　陳新華

摘? 要：高空沖擊波超壓的計算方法目前尚處于空白階段，該文基于沖擊波相似理論，利用前人對各種不同介質沖擊波超壓的傳播計算方法，計算分析沖擊波超壓隨介質密度改變的變化規律，提出空氣沖擊波超壓隨密度變化的計算模型，并對模型進行了運用計算及驗證，驗證結果理想。

關鍵詞：沖擊波超壓? 空氣? 介質? 密度

中圖分類號：O382 ? ?文獻標識碼：A 文章編號：1672-3791（2019）11（b）-0057-04

Abstract： The calculation method of the overpressure of air blast wave in high altitude is still in the blank stage. Based on the similarity theory of blast wave， this paper uses the method of calculating the overpressure of blast wave in different media to calculate and analyze the law of the change of the overpressure of blast wave with the change of the density of medium， and puts forward the calculation model of the change of the overpressure of air blast wave with the change of the density of air. This paper calculates and verifies the model. The results are satisfactory.

Key Words： The overpressure of blast; Air; Media; Density

描述爆炸產生的沖擊波在空氣中傳播特性參數主要有峰值超壓（即沖擊波峰值壓力與環境壓力之差）、正壓作用時間和比沖量等。其中空氣沖擊波峰值超壓大小是衡量爆炸事故對目標破壞力大小的重要特征參數。

對于爆炸沖擊波在常見介質中的傳播規律，20世紀80、90年代我國學者已有了較為系統的研究[1-4]，近些年針對工程實際應用又有了新的發展[5～8]，但前人只是針對某種連續介質來研究沖擊波超壓的特性，不同介質之間沒有連續性。該文將基于沖擊波相似理論，利用前人對各種不同介質沖擊波超壓的傳播計算方法，計算分析沖擊波超壓隨介質密度改變的變化規律，提出空氣沖擊波超壓隨密度變化的計算模型。

1? 幾種典型的空氣沖擊波超壓計算模型

（1）離爆心比較近的情況。

Науенко和Петроский提出的計算模型：

（1）

Henrych 給出的計算模型：

（2）

（3）

（2）離爆心比較遠的情況。

（4）

式中，△Pm為沖擊波峰值超壓，MPa;mT為液體燃料TNT當量，kg;r為計算點距爆炸中心的距離，m;h為爆炸點的高度，m。

這兩種計算模型均只適用于低空的空氣沖擊波超壓計算。

2? 考慮空氣密度影響的沖擊波超壓計算模型修正方法

方程（4）是低空爆炸空氣中沖擊波峰值超壓的計算式，記此時空氣密度為1.225kg/m3。

方程（5）是水中爆炸沖擊波峰值超壓的計算式，記此時水的密度為1000kg/m3。

（5）

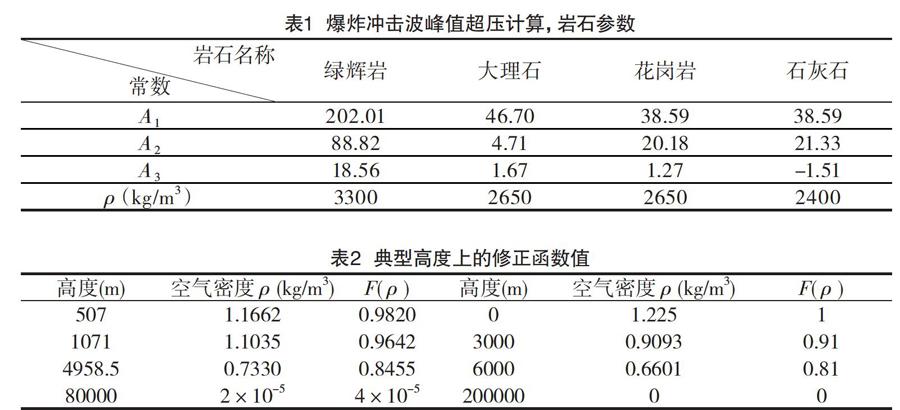
方程（6）是巖石中爆炸沖擊波峰值超壓的計算式，巖石參數見表1。

（6）

當mr一定，取一組不同的r值，利用方程（4）（5）（6）則可以計算得到在特定的R（此時R=r/）值下，沖擊波在空氣、水和巖石中的超壓值。即得到了不同介質密度對應的沖擊波超壓值。

圖1為沖擊波超壓隨介質密度變化的擬合曲線。由圖1可見，取不同R值得出的沖擊波超壓隨介質密度變化的曲線是不同的，但形狀極為相似，均可理解為指數函數。

為了便于清楚地分析圖1（a）中劃圈部分的曲線，將圖1（a）中R值小于2.5的幾條曲線去掉，如圖1（b）所示。

圖1在橫坐標密度大于0.5時很好地反映了介質密度對于沖擊波超壓的影響情況。但在橫坐標小于0.5時，由于沖擊波變得非常弱，各曲線都接近水平，密度對于沖擊波超壓的影響反映不明顯。

圖2為介質密度取0～1.2kg/m3時沖擊波超壓隨介質密度變化的擬合曲線小密度段。同理，為了便于清楚地分析圖2（a）中劃圈部分的曲線，將圖2（a）中R值小于2.5的幾條曲線去掉，如圖2（b）所示。

由圖2擬合出密度較小，適合于對空氣沖擊波超壓隨空氣密度變化的修正函數，即：

F（ρ）=0.5734ρ3-1.8081ρ2+2.1708ρ? ? ? ? ? ? ? ? ? ? ? ? ?（7）

該修正函數的曲線如圖3所示，由圖可知，當密度介于0和1.225g/m3之間時，修正函數值介于0和1之間，并且增長速度逐漸減慢。當密度大于1.225kg/m3時，此時傳播介質發生改變，已經不是空氣，曲線出現拐點。

將式（7）代入式（4）得到空氣沖擊波超壓計算的修正模型，即：

△Pm高空=△Pm地面·F（ρ）

（8）

3? 模型的運用及驗證

表2是由式（7）計算出的一些典型高度上的修正函數值。

表2數據表明，在高度3000m處，空氣沖擊波超壓的修正系數為0.91，在高度6000m處，空氣沖擊波超壓的修正系數為0.81。根據國外文獻[9]的介紹，海拔3000m處的空氣沖擊波超壓要比海平面空氣沖擊波超壓低9%，而海拔6000m處的空氣沖擊波超壓要比海平面空氣沖擊波超壓低19%。兩者之間非常吻合，表明該文提出的修正模型是可用的。

參考文獻

[1] 李翼祺，馬素貞.爆炸力學[M].北京：科學出版社，1992.

[2] 孫錦山，朱建士.理論爆轟物理[M].北京：國防工業出版社，1995.

[3] 北京工業學院八系.爆炸及其作用[M].北京：國防工業出版社，1981.

[4] 葉序雙.空氣中、水中爆炸理論基礎（上冊）[M].南京：中國人民解放軍工程兵工程學院訓練部，1985.

[5] 張國偉.終點效應及其應用技術[M].北京：國防工業出版社，2006.

[6] 隨樹元，王樹山.終點效應學[M].北京：國防工業出版社，2000.

[7] 張寶坪，張慶明，黃風雷.爆轟物理學[M].北京：兵器工業出版社，2006.

[8] 張國偉，徐立新，張秀艷.終點效應及靶場試驗.北京：北京理工大學出版社，2009.

[9] Baker WE，Kuiesz JJ，Ricker RE.Workbook for predicting pressure wave and fragment effects of exploding propellant tanks and gas storage vessels[Z].NASA CR-134906，1977.