星載拋物面天線視在相位中心確定方法及應用

沈迎詠，高晶波，王 聰

(哈爾濱工業大學航天學院，哈爾濱 150001)

0 引言

隨著通信、雷達、人造衛星的發展，天線在國防領域的應用越來越廣泛，由于拋物面天線具有發射功率大、副瓣較低、結構簡單易加工、相關技術較成熟等優點[1]，常常被選擇作為發射天線或陣列單元。例如SAR衛星[2-3]采用大口徑可展開拋物面天線，饋源處安置喇叭天線，它的主要任務是通過微波成像的方式獲取地面目標的圖像情報信息，結合多種成像工作模式，實現對地面目標的詳查和普查。為了適應微波載荷提出的空間高分辨率、定位高精度、探測高靈敏度的參數指標，衛星天線需具備更高的指向精度[4]和穩定度[5]，而這些均與天線的相位中心密切相關。

相位中心在衛星天線研究中占有重要地位。為了實現反射面天線高增益和低副瓣電平的目標，必須把饋源喇叭天線相位中心[6-10]放置在反射器拋物面的焦點處。由于喇叭天線的輻射場不是理想的球面波，因此不存在嚴格的相位中心，但實際應用中仍需要確定一個近似的相位中心，并使其與拋物面焦點重合，以便得到最大的天線增益，該點便稱為“視在相位中心”[11-13]。在實際應用中將對視在相位中心進行測量，來替代物理意義上的相位中心。確定喇叭天線的視在相位中心有兩種方法：一種是實驗方法[14]，該方法將喇叭天線放置在拋物面天線的焦點附近做軸向移動，確定拋物面天線的增益最大(或者主瓣寬度最窄)時的喇叭天線的位置，從而確定視在相位中心。實驗方法雖然簡單，但需要進行重復的實驗，工作量大，效率低。另一種是從理論近似分析求得[3]，該分析需要計算拋物面天線主波束一定角度范圍內的多個測點的遠場相位方向圖的相位波動值，當某點方向圖的相位波動最小時，這個點就稱為天線的視在相位中心，此時拋物面天線視在相位中心的計算公式很復雜，不能直接應用于工程實際中。因此，本文結合具體的實際問題，建立衛星有限元模型，基于多體系統動力學在軌仿真分析，利用拋物面天線的工作原理以及視在相位中心的定義，擬合拋物面天線在機動過程中的視在相位中心位置，并利用最小二乘法分析視在相位中心坐標偏移量。對比分析有阻尼器和無阻尼器兩種連接方式對天線視在相位中心偏移量的影響，為拋物面天線指向精度的研究提供參考。

1 拋物面天線工作原理與視在相位中心

拋物面天線是由拋物面反射器和位于其焦點處的饋源組成的面狀天線，饋源處通常安置喇叭天線。如圖1所示，拋物面天線有以下兩個重要的性質[15]：1)由焦點F發出的射線經反射器拋物面反射后，所有反射線都與拋物面軸線平行；反之，當平行射線沿拋物面軸線入射到拋物面上時，被拋物面反射后，其反射線均匯聚于焦點處。2)由焦點發出并經拋物面反射的各條射線，到達垂直于拋物面軸線任一平面時的波程相等，因此，垂直于軸線的平面為等相位面。這兩個性質的證明如下：

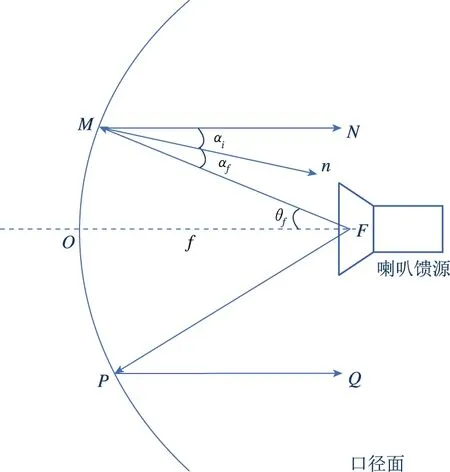
圖1 反射器在xz平面內的橫截面Fig.1 Cross section of the reflector in the xz plane

O點為反射器拋物面的頂點，F為焦點，焦距為f，M為反射器表面上一點，M點與焦點F的距離為rf，該拋物線用極坐標rf,θf可表示為

(1)

(2)

歸一化得

(3)

則入射角αf與反射角為αi可以求得

(4)

(5)

因此可以得出

(6)

(7)

性質1)由此可以證明。

下面證明性質2)，從焦點到口徑面的總長度為

FM+MN=rf+rfcosθf=rf1+cosθf=2f

(8)

因為總長度是恒定的，從焦點處的饋源到達口徑平面的波相位也恒定。

以上兩個重要的性質是拋物面天線的工作基礎。基于以上性質，拋物面天線用作發射天線時，位于焦點F處的弱方向性饋源向拋物面輻射球面波，經拋物面反射的電磁波變成沿軸線傳輸的截面約為拋物面口徑的平面電磁波(相位相同)，使反射器口面場形成均勻分布，均勻口面場將產生方向性輻射場，反之，如果把拋物面天線用作接收天線，入射波又是平行于拋物面軸線的平行波形式，經反射器反射后則會把平面波轉換成球面波傳送到位于焦點位置的饋源(相位中心)，形成聚集接收，增加其接收信號的強度。因此，從物理現象上電磁波相當于從一點發出或者被同一點接收，定義此點即為拋物面天線視在相位中心。

2 整星多體系統動力學仿真

整星多體模型包括星本體、天線系統、左右對稱的帆板等。本文重點研究天線視在相位中心，因此將星本體視為剛體，饋源簡化為圓形平面薄板，如圖2所示。整星在方位向(X軸)上定軸轉動，范圍為0°～90°，這個過程中保持動中成像，有指向精度與穩定度要求，然后成像結束，恢復初始位置，調姿曲線如圖3所示。本文仿真環境是：整星受到距離向即x軸正方向的飛輪干擾力、飛輪干擾力矩以及太陽電池陣驅動機構(SADA)擾動。飛輪干擾力及干擾力矩采用四階諧波疊加

(9)

其中，m(t)為擾動力或擾動力矩；n為模型中含有的諧波數；Ω為轉速；hi為第i次諧波數；Ci為與mt相應的第i次諧波的幅值，單位為N/Hz2或N·m/Hz2；αi為隨機相位角，假設均勻分布在0,2π。本文仿真分析中，飛輪轉速為6000r/s，飛輪諧波系數如表1所示，飛輪干擾力如圖4所示，飛輪干擾力矩如圖5所示。考慮SADA擾動時，由于軸向干擾力矩為主要擾動因素，徑向干擾力為次要擾動因素，本次仿真忽略SADA干擾力的影響，只建立SADA擾動力矩的模型，干擾力矩的均值為2N·m，方差為0.3(N·m)2，如圖6所示。

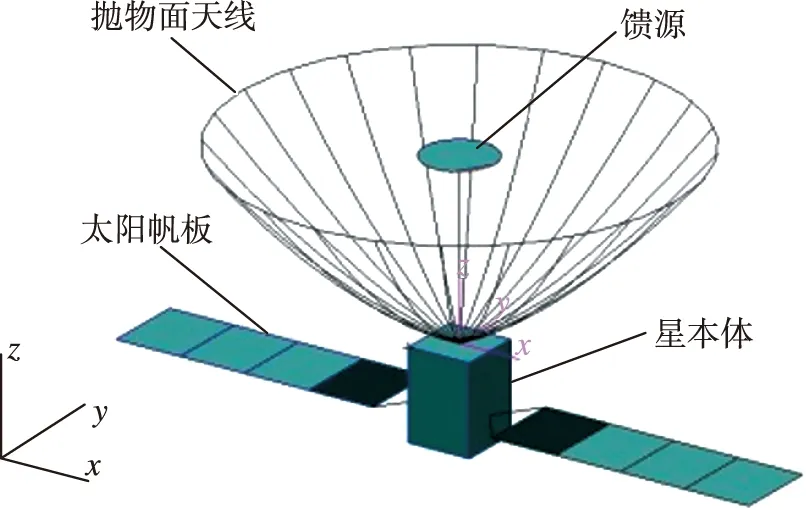
圖2 整星仿真模型Fig.2 Whole star simulation model

圖3 整星調姿曲線Fig.3 Whole star attitude curve

圖4 飛輪干擾力曲線Fig.4 Flywheel interference force curve

圖5 飛輪干擾力矩曲線Fig.5 Flywheel interference torque curve

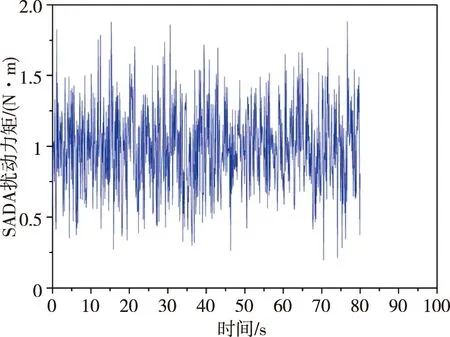
圖6 SADA擾動力矩曲線Fig.6 SADA interference torque curve

采用不同的連接方式進行仿真分析，各仿真工況如表2所示，分析不同工況下視在相位中心的位置。

表1 飛輪諧波系數

表2 多體動力學仿真工況

3 天線視在相位中心的計算

采集不同仿真工況下反射器拋物面標志點坐標，利用最小二乘法擬合拋物面方程。仿真過程中，坐標原點放置在天線底部中心，采集xz面與yz面天線內反射表面標志點坐標，分別擬合計算焦點(x0，z0)和(y90，z90)，得到視在相位中心(x0，y90，(z0+z90)/2)。下面以天線不動時為例求解天線視在相位中心。

初始時刻xz面與yz面天線內反射面標志點坐標如表3、表4所示，利用最小二乘法分別擬合標志點如圖7中(a)、(b)所示，可得xz面擬合曲線為

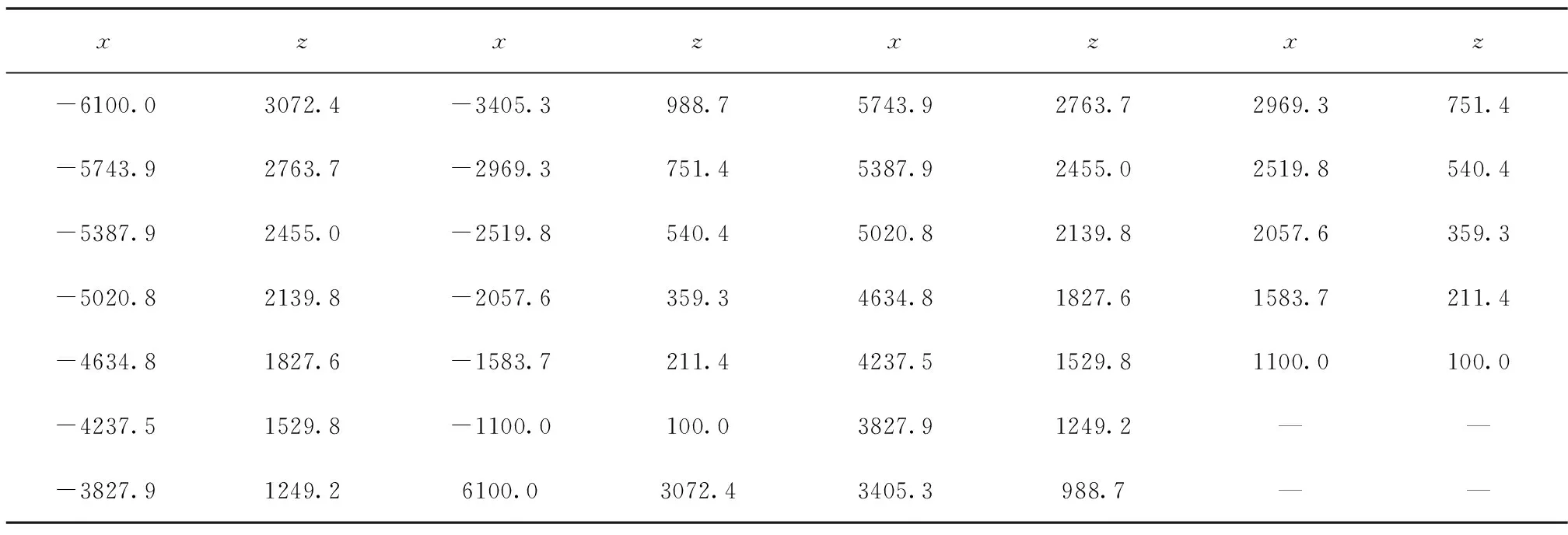
表3 xz面內標志點坐標

表4 yz面內標志點坐標

z=8.3443×10-5x2-5.7066×10-8x+1.5001

(10)

得其焦點x0,z0為(3.4149×10-2，3011.0739)，yz面擬合曲線為

z=1.8343×10-5y2+4.2329×10-6y+1.5007

(11)

得其焦點y90,z90為(-0.0253，3011.0582)，即可得到視在相位中心(x0，y90，(z0+z90)/2)為(3.4149×10-2，-0.0253，3011.0661)。

(a) xz面內擬合面

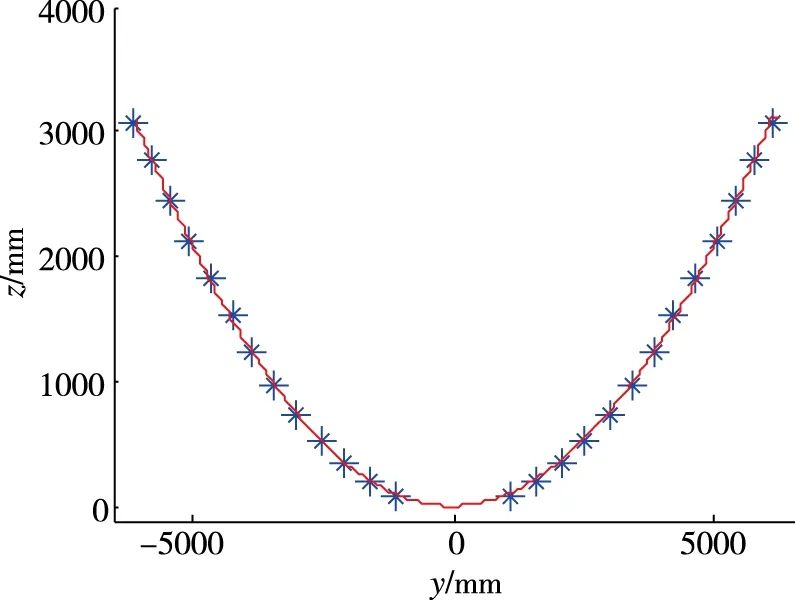
(b) yz面內擬合面圖7 拋物面擬合圖Fig.7 Parabolic fitting

依照此方法可以擬合得到天線機動過程中的相位中心，利用最小二乘法擬合可得視在相位中心坐標偏移量，從而可得天線機動過程中的視在相位中心坐標范圍。進行仿真工況1時，天線與中心平臺無阻尼器連接，擬合可得視在相位中心坐標偏移量如圖8所示。從圖8中可以看出，視在相位中心在天線機動過程中受到飛輪干擾以及SADA擾動的影響，x坐標的偏移量范圍Δx∈-0.2169,0.2358，y坐標的偏移量范圍Δy∈-0.0184,0.0249，z坐標的偏移量范圍Δz∈-0.1569,0.2093，由于整星在方位向(x軸)定軸轉動，因此y坐標偏移量最小。

圖8 無阻尼器連接時天線視在相位中心偏移量Fig.8 The deflection of the antenna in the phase center when the damper isn’t connected

進行仿真工況2時，天線與中心平臺有阻尼器連接，擬合可得視在相位中心坐標偏移量如圖9所示。從圖9中可以看出，視在相位中心在天線機動過程中受到飛輪干擾力、干擾力矩以及SADA擾動的影響，x坐標的偏移量范圍Δx∈-0.0988,0.0953，y坐標的偏移量范圍Δy∈-0.0160,0.0170，z坐標的偏移量范圍Δz∈-0.0011,0.0010，由于阻尼器的作用，視在相位中心的坐標偏移量都減小，其中z坐標偏移量最小。

圖9 有阻尼器連接時天線視在相位中心偏移量Fig.9 The deflection of the antenna in the phase center when the damper is connected

對比兩種工況下的視在相位中心的變動范圍，如表5所示，整星在方位向(X軸)上定軸轉動，范圍從0°～90°，受到距離向即x軸正方向的飛輪干擾力、干擾力矩以及SADA擾動，有阻尼器連接的天線視在相位中心的振動量明顯小于無阻尼器連接的情況，阻尼器連接方式的天線視在相位中心最大偏移量Δz的變化量比無阻尼器連接的天線降低了兩個數量級。

表5 視在相位中心偏移量對比

4 結論

本文針對星載拋物面天線成像過程中對波束的指向精度的要求，提出了天線視在相位中心的確定方法，并利用多體系統仿真方法研究了衛星機動過程中的視在相位中心范圍及影響因素，得到以下結論：

1) 給出了拋物面天線視在相位中心的定義，并利用最小二乘法擬合得到了天線視在相位中心的位置。

2)天線視在相位中心的偏移量的分量受天線運動方向的影響，整星在方位向(X軸)上定軸轉動，x坐標偏移量最大。

3)天線在機動過程中，無阻尼連接的天線視在相位中心的z偏移量在(-0.1569，0.2093)范圍內，有阻尼器連接的天線視在相位中心的z偏移量在(-0.0010，0.0011)范圍內，最大偏移量降低了兩個數量級；無阻尼連接的天線視在相位中心x偏移量在(-0.2169,0.2358)范圍內，有阻尼器連接的天線視在相位中心的x偏移量在(-0.0988,0.0953)范圍內，最大偏移量降低一個數量級，阻尼器對天線視在相位中心x,z方向的震蕩有明顯的抑制。

以上不同工況的仿真結果表明，本文所提出的方法能夠準確給出機動過程中拋物面天線視在相位中心，為拋物面天線指向精度和穩定度分析提供理論基礎。