艦船水下爆炸沖擊動彎矩工程化預報

郭建軍，趙玉麟，張 皓，李元泰，夏 風

(1. 武漢第二船舶設計研究所，湖北 武漢 430064；

2. 華中科技大學 船舶與海洋工程學院，湖北 武漢 430074)

0 引 言

隨著各國海軍艦船需求的不斷提升以及民用新船型的不斷開發，對艦船在極端情況下的強度要求越來越高。艦船總強度是船舶設計人員首要關心的重要問題，現行設計和研究船舶總強度時一般只計及波浪載荷、抨擊及上浪載荷等外載荷，而對于軍用艦船以及如浮式核電船等特殊船舶，水下爆炸下的艦船總強度問題不容忽略。與一般外載荷下的船體總縱強度問題相比，水下爆炸下的艦船總強度必須要計及沖擊振動彎矩的影響，其數量級甚至比波浪載荷誘導下船體總縱彎矩更高。因此本文針對船體水下爆炸沖擊振動彎矩進行研究。

水下非接觸爆炸載荷通常分為沖擊波和氣泡脈動載荷，沖擊波壓力峰值高持續時間短，而氣泡脈動壓力峰值較低持續時間長，二者先后共同作用于船體造成船體毀傷效應。水下爆炸載荷作用下船體的動態響應問題前人已有了不少研究[1-4]，主要集中在對于水下爆炸氣泡脈動下的船體鞭狀振動問題的研究，且并沒有經過實船試驗驗證。結合當前理論與試驗研究，本文針對水下爆炸船體沖擊振動彎矩問題進行研究，應用泰勒平板流固耦合理論[5]基于模態疊加理論的船體梁模型對船體沖擊振動彎矩進行快速化預報，在預報多種船型的基礎上探索沖擊振動彎矩的規律，并給出沖擊振動彎矩的經驗公式，為工程設計人員的初步設計校核提供參考。

1 水下爆炸船體沖擊動彎矩分析

1.1 簡化模型

水下爆炸作用下船體主要受重力、浮力、爆炸載荷、船體慣性力等綜合作用，靜水中重力和浮力是一對平衡力，船體振動引起浮力的變化可簡化為浮力彈簧的形式模擬，船體所受爆炸載荷需要考慮船體水下爆炸作用下流固耦合作用，慣性力由達朗貝爾原理得到。采用船體慣性矩等效和質量等效形式把船體等效為變截面等值船體梁，這樣等值梁在爆炸載荷、浮力變化力和慣性力的聯合作用下產生沖擊振動彎矩。其中，垂向附連水質量采用陶德經驗公式計算，浮力彈簧根據船體水線面面積近似求得。船體梁模型如圖1所示，經模態分析確保船體梁模型的有效性。

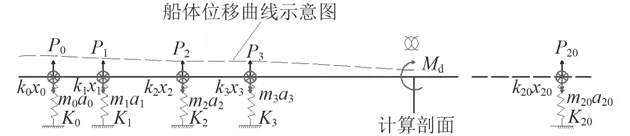
圖1 水下爆炸船體梁模型示意圖Fig. 1 Schematic diagram of ship hull girder underwater explosion

1.2 舷外水的影響

舷外水對船體水下爆炸的影響主要體現3個方面：船體振動引起浮力與重力的不平衡，船體附連水質量以及船體所受爆炸載荷需要考慮船體運動的影響。

艦船在遭受水下非接觸爆炸載荷作用下產生的船體垂向振動響應會引起浮力變化，這種變化也應計入船體剖面動彎矩計算。采用彈簧等效的方法來模擬此種變化，以彈簧剛度值來代替每站單位吃水引起的浮力變化。船體因沖擊載荷在垂向的位移響應導致的吃水變化微小，故采用船體各站水線面在垂向的單位長度的浮力近似代替實際的浮力變化。由此得出水線面各站的彈簧所模擬的剛度計算式：

式中： ρ為海水密度，1 025 kg/m3； g為重力加速度，9.81 m/s2； A為各站水線面積，m2。

舷外水影響的另一個重要方面是附連水質量，采用托德公式通過查表求得，單位長度附連水質量的表達式為：

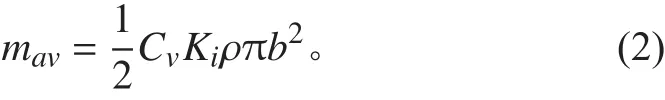
式中：ρ為水的密度，取1 025 kg/m3； b為計算剖面處的水線半寬； CV為無因次修正系數，垂向振動時，船舶水下部分橫剖面形狀不同于橢圓而引入的，取決于寬度吃水比和浸沒剖面面積系數 β； β=S/2bd，為計算剖面處的最大吃水，為浸沒剖面面積； Ki為三維流動引入的無因次修正系數，對垂向振動，與船的長寬比L/B及振動諧調數有關[5-6]。

水下爆炸載荷的確定是艦船沖擊動彎矩分析計算的重要方面。前人對爆炸載荷進行了大量的研究，有代表性的是Geers and Hunter模型[7]，對水下爆炸沖擊波與氣泡載荷均有較好的描述，本文中沖擊波以經驗公式，氣泡模型以Geers and Hunter模型公式為基礎計算水下爆炸自由場中壓力載荷，根據泰勒平板方程來計及船體運動對船體載荷的影響，并且忽略水面截斷效應以及沖擊波透射作用的影響[8-9]。應用Taylor平板理論求解流固耦合界面處的壓力方程為：

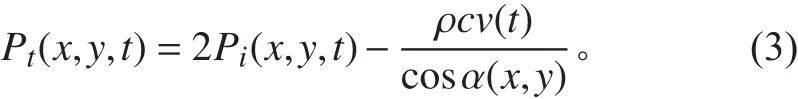
式中： Pi(x,y,t)為平板上任意一點受到的球面波入射壓力； v(t)船體運動垂向速度； cosα為入射波與垂直方向的夾角余弦值；c為水中沖擊波波速。

式（3）為爆炸載荷計算公式為單元載荷，考慮將每站單元力的疊加，計及波傳播的延時效果，通過編寫程序計算可迭代出船體每站的激勵載荷。根據文獻[10]中-3.0 MPa的空化臨界壓力，本文的爆炸載荷不計空化的影響。

1.3 模態疊加法求解沖擊動彎矩

采用有阻尼多自由度系統受迫振動的運動方程

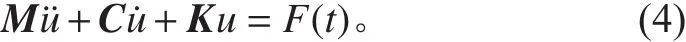
式中：M為質量矩陣；C為阻尼陣；K為剛度矩陣。

經過模態陣型的坐標變換，即 u=φq ，得到如下運動方程：

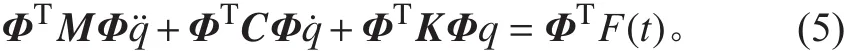
式中： Φ為陣型矩陣； q為主坐標。

聯立式（3）和式（5），即船體外殼某站所受載荷方程與船體振動方程聯立求解出船體梁響應和船體所受載荷，同時聯立動彎矩的微分方程，得到如下迭代公式：

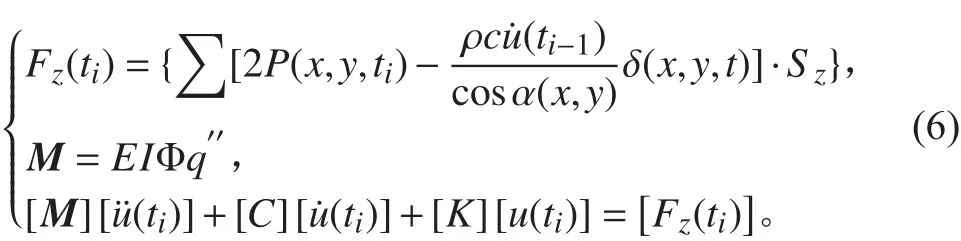
式中： δ(x,y,t)為時間延遲輔助函數； sz為船體外板網格單元的垂向投影面積。

采用紐馬克平均加速度法迭代求解上述方程式[11]，可獲得滿足工程應用的船體梁響應特性的數值解。

1.4 試驗驗證

以某實船試驗為例，選取沖擊因子為0.55，工況為船中右舷一側橫向偏離50 m，爆點攻角為30°，其中阻尼采用經典阻尼，取文獻[12]中相似船型的阻尼比0.04，經過編程計算出等值梁在爆炸載荷作用下各典型橫剖面無量綱化取前3階總和的動彎矩，并與無量綱化的實船試驗值對比分析，如圖2和表1所示。

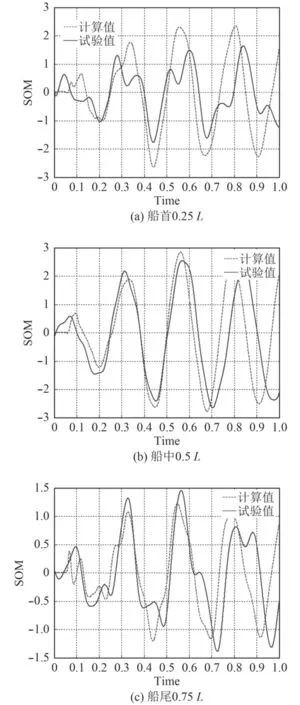
圖2 動彎矩對比圖Fig. 2 The contrast diagram of shock vibration bending moment

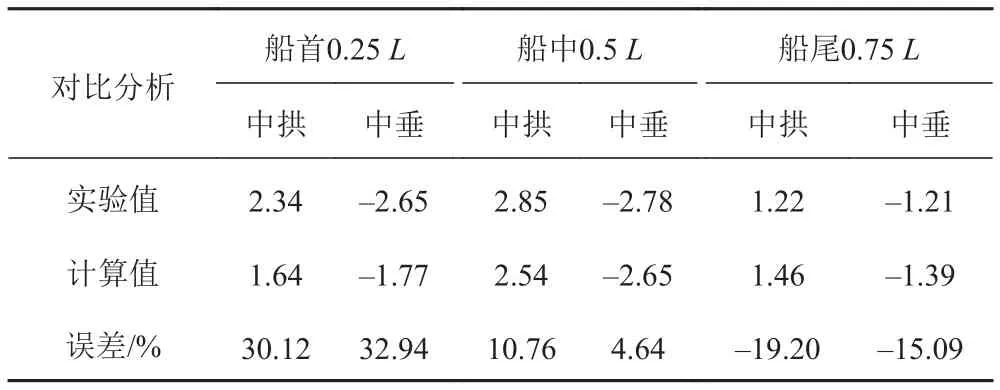
表1 動彎矩對比表Tab. 1 The comparison chart of shock vibration bending moment

通過對比可知采用該理論計算值與實驗值在船中處吻合較好，誤差在10%以內，首部1/4處計算值偏小約30%。船尾1/4處計算值偏大約20%，誤差在工程應用可接受的范圍之內。由于該方法理論模型簡單，計算過程程序化，可在工程精度范圍內快速計算船體水下爆炸載荷作用下的動彎矩，并能夠應用于初步設計中計及水下爆炸沖擊動彎矩的總強度校核。

2 不同船型的沖擊動彎矩工程化預報

針對不同船型的沖擊動彎矩進行快速化工程預報，以6艘不同船型和排水量的艦船作為典型計算模型，設置多種水下爆炸工況，分別計算各型艦船在不同工況下的沖擊動彎矩，將結果進行分析對比，探究沖擊動彎矩隨在不同水下爆炸工況的變化規律，以及動彎矩在相同工況下隨艦船標準排水量變化的規律。

2.1 參數設置

選擇6種不同排水量的艦船分析在相同水下爆炸載荷作用下的沖擊動彎矩，表2為各船的基本參數。

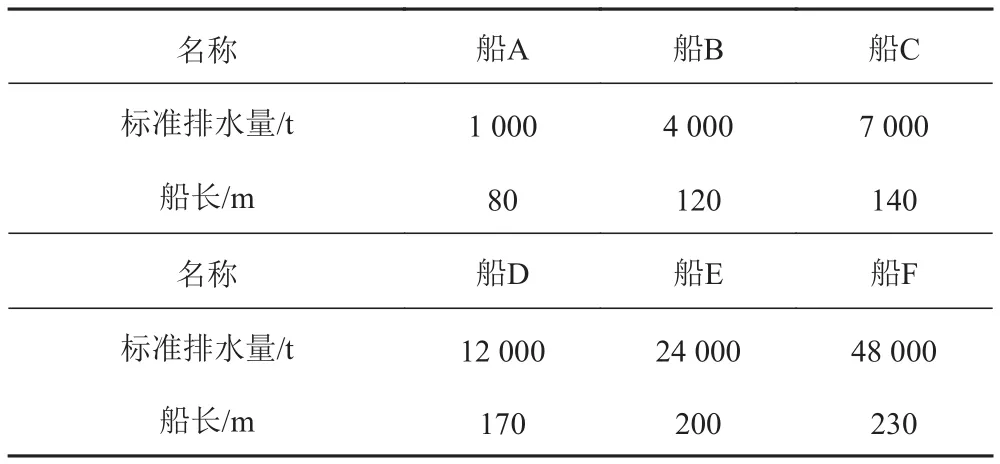
表2 各艦船的主要參數Tab. 2 Main parameters of typical ships

各船分別設置4種不同沖擊因子的計算工況，藥包質量為1 000 kg，藥包的位置設置在各船船中剖面處，攻角統一設定為45°，采用龍骨沖擊因子，不同工況下的具體參數設定如表3所示，表達式如下式：

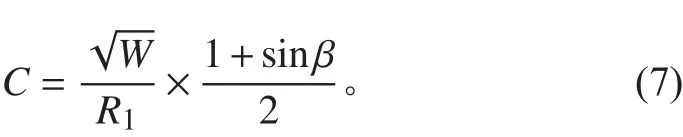
式中： W 為藥包質量，kg； β為爆炸攻角。

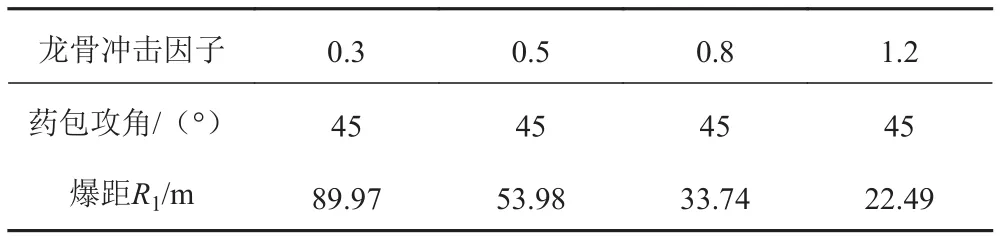
表3 水下爆炸工況參數設置表Tab. 3 Parameter of conditions underwater explosion

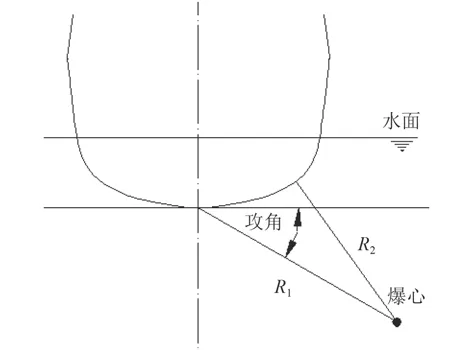
圖3 沖擊因子工況示意圖Fig. 3 Schematic diagram of keel shock factor (KSF)

2.2 計算結果

計算得到不同工況下6個船型3個典型剖面的動彎矩，以船A在沖擊因子為0.3工況下的動彎矩為例，其各剖面的前3階總動彎矩如圖4所示。

由圖4可知，船A在水下爆炸沖擊因子為0.3工況下的沖擊動彎矩在阻尼的作用下衰減趨勢明顯；船中剖面的沖擊動彎矩為最大，首尾L/4剖面的動彎矩約為船中部位的一半，且船中部位的動彎矩低階成分更大。

2.3 結果分析

取各工況下6個船型典型剖面的總動彎矩最大值，并比較在相同工況下不同船型各剖面的動彎矩隨標準排水量的變化。中拱和中垂狀態下各剖面動彎矩隨艦船標準排水量的變化曲線分別如圖5～圖8所示。

從上述4種沖擊因子工況下的動彎矩隨艦船標準排水量變化曲線圖中可以得出，中拱和中垂狀態下船首、船中和船尾3個校核剖面的動彎矩變化一致，相同沖擊因子工況下的動彎矩均隨著標準排水量的增大而呈顯著上升趨勢，不同標準排水量的艦船在相同工況下產生的動彎矩數量級也不同，而標準排水量接近的艦船動彎矩數量級則較為接近，所以在快速考核分析某標準排水量艦船的動彎矩時，可參考標準排水量相近艦船的動彎矩即可。

3 沖擊動彎矩預報的經驗公式

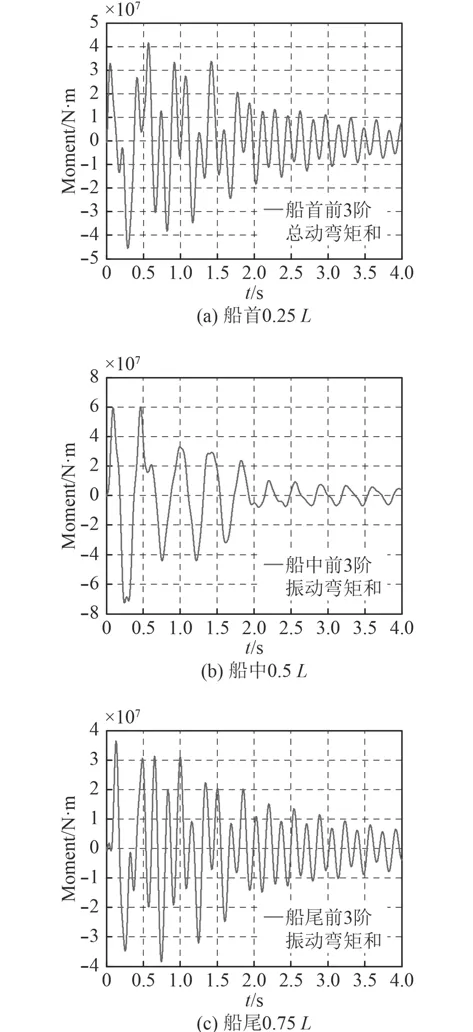
圖4 船A沖擊動彎矩（KSF=0.3）Fig. 4 Shock vibration bending moment of ship A (KSF=0.3)

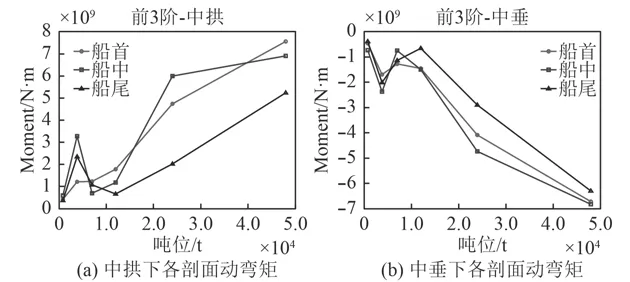
圖5 沖擊因子0.3時動彎矩隨排水量的變化曲線Fig. 5 SVBM curves varying with displacement (KSF=0.3)

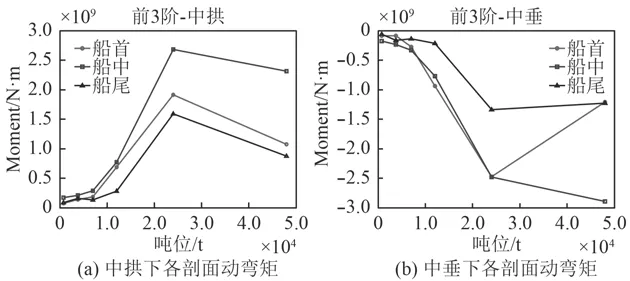
圖6 沖擊因子0.5時動彎矩隨排水量的變化曲線Fig. 6 SVBM curves varying with displacement (KSF=0.5)

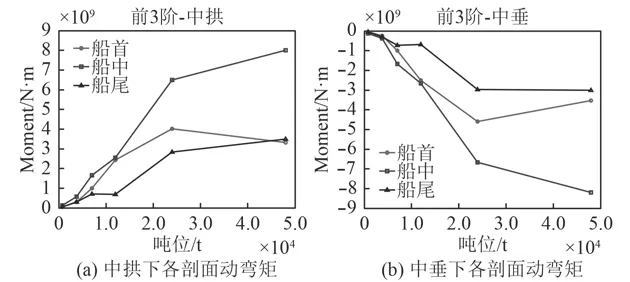
圖7 沖擊因子0.8時動彎矩隨排水量的變化曲線Fig. 7 SVBM curves varying with displacement (KSF=0.8)

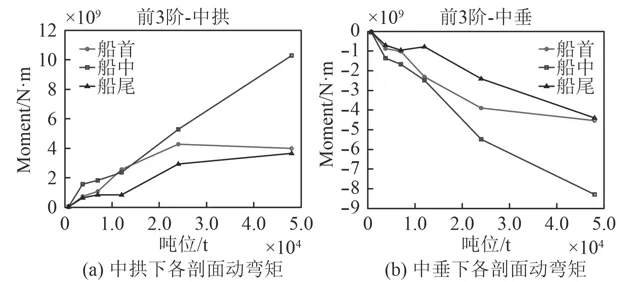
圖8 沖擊因子1.2時動彎矩隨排水量的變化曲線Fig. 8 SVBM curves varying with displacement (KSF=1.2)

通過上述6種不同船長及排水量艦船在水下爆炸中遠場不同沖擊因子下的計算結果，發現總縱動彎矩值大致隨排水量或船長呈一定規律。在大量計算工況的基礎上，去除明顯與相近船型動彎矩值差異較大的值，并借鑒勞氏規范中有關波浪彎矩的經驗公式，在對其余結果進行定性分析的基礎上得出沖擊動彎矩主要與艦船水線長、排水量、中橫剖面系數等船型系數以及龍骨沖擊因子等因數有關，結合勞氏規范中波浪抨擊彎矩經驗公式的形式，通過分析得到可以近似估算某船型在某一沖擊因子下沖擊動彎矩的經驗公式，能為艦船初步設計提供參考，估算公式如下：

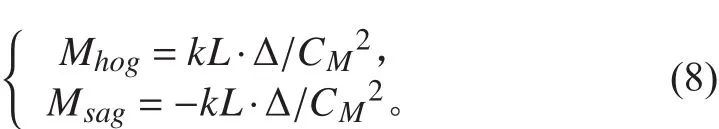
式中： CM為船的中橫剖面系數為船的中橫剖面面積，m2；B為型寬，m；T為吃水，m；為水線長，m；為排水量，kg；為沖擊因子修正系數，取值如下：

其中，為龍骨沖擊因子（C ≥0.5）。

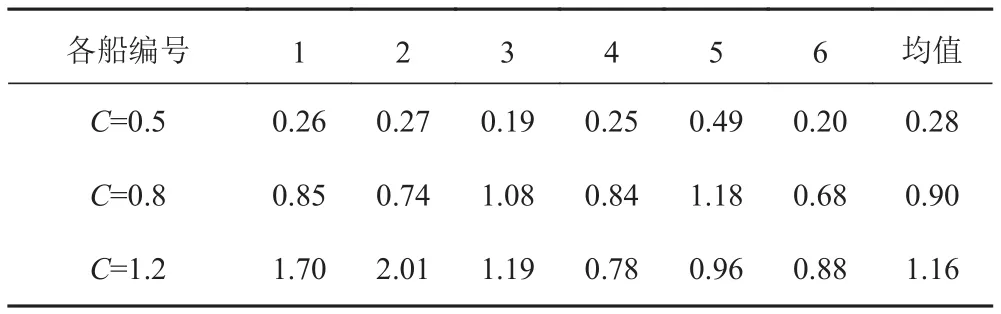
表4 中拱狀態沖擊因子C與系數K的關系表（單位N·m）Tab. 4 The relationship between coefficient k and KSF C in hogging condition

利用上述擬合出的公式，計算各型船在沖擊因子為0.8時的沖擊動彎矩，并對比分析，如表6和表7所示。

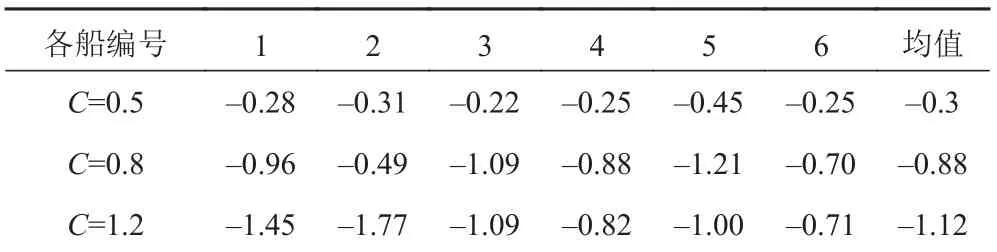
表5 中垂狀態沖擊因子C與系數K的關系表（單位N·m）Tab. 5 The relationship between coefficient k and KSF C in sagging condition

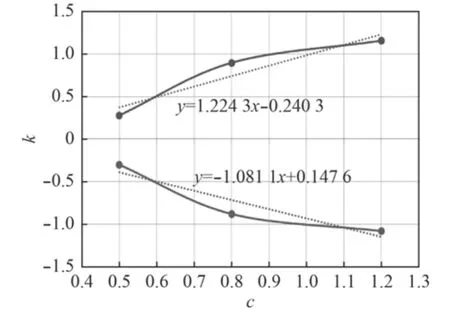
圖9 系數k與沖擊因子C的線性擬合關系圖Fig. 9 Linear fitting relation graph between coefficient k and KSF C

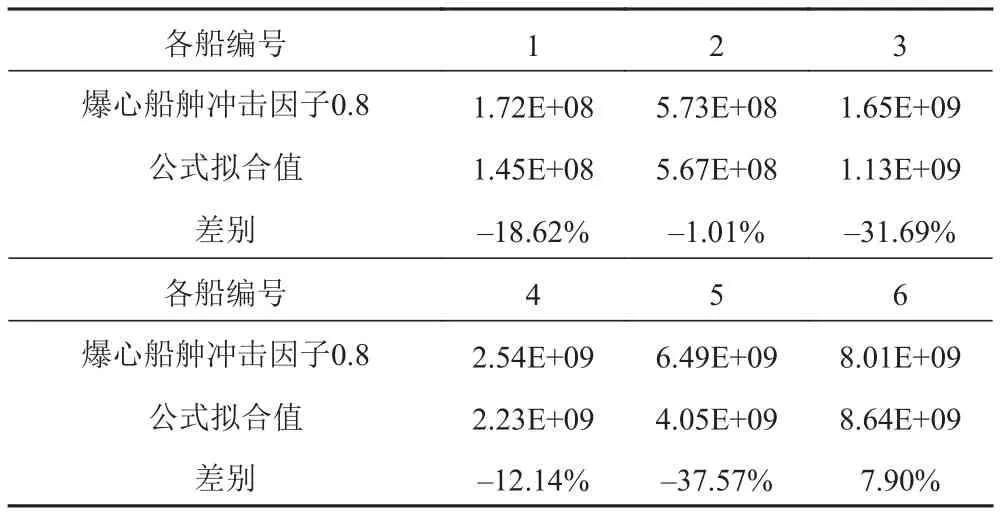
表6 沖擊因子0.8時中拱狀態船中動彎矩值比較（單位N·m）Tab. 6 The contrast diagram of shock vibrationbending moment in hogging condition (KSF=0.8)

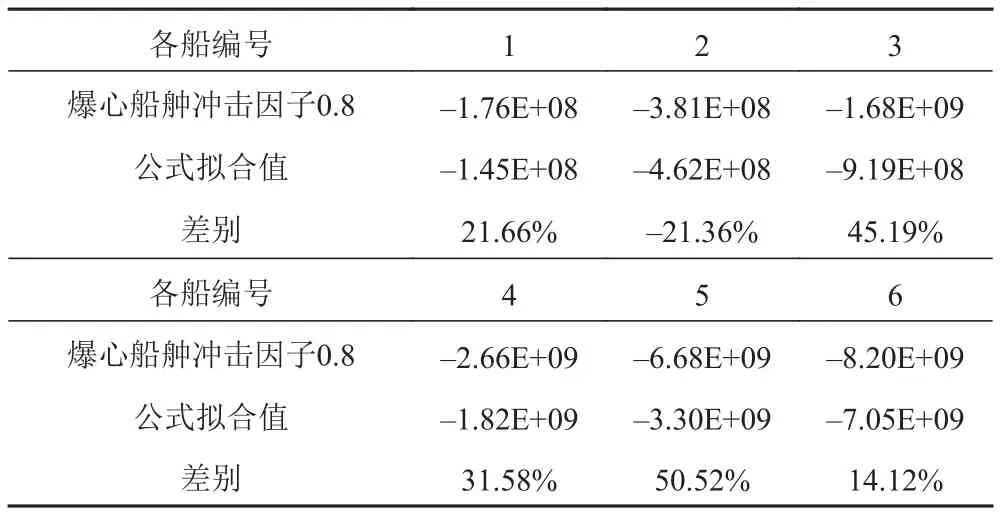
表7 沖擊因子0.8時中垂狀態船中動彎矩值比較（單位N·m）Tab. 7 The contrast diagram of shock vibrationbending moment in sagging condition (KSF=0.8)

可以看出，公式得到的結果與計算值差別波動較大；隨著沖擊因子的增大，即爆距減小時，公式得到的結果與計算值差別波動較為平緩，因此該經驗公式可為艦船初步設計中的沖擊動彎矩估算提供一定的參考。

4 結 語

通過船體等效為船體梁計算水下爆炸沖擊動彎矩，可以得到以下結論：水下中遠場爆炸船體等值梁模型動彎矩計算方法的可行性，該工程計算方法的精度從工程角度來看是可以接受的；針對若干不同船長不同排水量的若干艘船舶進行沖擊動彎矩的快速化預報，并分析動彎矩隨船舶標準排水量的分布規律，相同沖擊因子工況下的動彎矩均隨著標準排水量的增大而呈顯著上升趨勢，不同標準排水量的艦船在相同工況下產生的動彎矩數量級也不同，而標準排水量接近的艦船動彎矩數量級則較為接近；給出簡化的沖擊動彎矩預報經驗公式，預報精度在工程應用上處于可接受的范圍內，可為艦船初步設計提供參考。