考慮連桿慣性參數的三缸發動機激勵建模與分析

左曙光，王 珺，周大為，閻 礁，安一領，吳旭東

(1. 同濟大學 汽車學院，上海 201804； 2. 泛亞汽車技術中心有限公司，上海 201201)

往復式內燃機是現代汽車的主要動力源，為汽車提供動力的同時也是一個主要的振動激勵源。為了滿足國家排放法規的限制以及節能減排的目標，目前越來越多的汽車上使用了小型化的三缸發動機。三缸發動機無法抵消曲柄連桿機構運動產生的不平衡慣性力矩，存在怠速抖動等振動問題，其NVH(Noise Vibration and Harshness)檢查性能較差[1]。在動力總成懸置系統的設計、優化過程中，準確計算振動激勵是進行系統設計的重要前提。隨著人們對于乘坐舒適性的重視，對懸置系統的設計提出了更高要求，需要準確地對發動機振動激勵進行建模解析。目前關于發動機動力學建模和激勵計算的研究大多針對偶數缸發動機，而三缸發動機的激勵階次成分復雜，這些方法無法準確反映三缸發動機實際運行狀態下的振動激勵特性，因此考慮需要對三缸發動機曲柄連桿機構進行動力學建模，求解其振動激勵。

發動機的振動激勵主要包含兩種成分：氣缸內氣體燃燒壓力而引起的繞曲軸軸線方向并向外傳遞的負載力矩以及活塞、連桿等零部件運動產生的慣性力、慣性力矩。對于三缸發動機而言，曲軸負載力矩為1.5階及其倍數，而慣性力及慣性力矩為1階及其倍數，二者振動能量相當，均需要準確建模計算。

目前，發動機振動激勵的理論計算中大多使用一種簡化的方法[2-5]，先研究單缸發動機的曲柄連桿機構，將連桿等效成位于活塞銷及曲柄銷處的兩個質量塊，與曲軸、活塞一起構成雙質量系統，根據運動學關系推導單缸發動機的激勵，然后根據多缸發動機各缸相位差推廣到多缸發動機，得到多缸發動機的振動激勵，這種方法進行了大量簡化，沒有充分考慮曲柄連桿機構部件的慣性參數，尤其是連桿，也沒有考慮各氣缸之間的氣體壓力、相位差等參數的差異，導致對于三缸發動機的激勵計算精度不足。密歇根大學的Hoffman等[6]基于多體動力學中的凱恩方法進行了發動機振動激勵的理論計算，建立了發動機缸體與曲柄連桿機構相互耦合的7自由度模型進而計算振動激勵，算法過于復雜，實際工程中不需要考慮發動機缸體對于曲柄連桿機構運動的影響，采用單向耦合的模型即可達到較高精度。伊朗的Fakhari等[7]基于拉格朗日法及牛頓歐拉方程詳細推導了曲柄連桿機構中活塞側向力、主軸承受力等，但對于動力總成來說，這些都是系統內力，不應計入振動激勵。何智成等[8]通過實驗對動力總成懸置系統的激勵進行了識別，建立了等效激勵參數模型，利用遺傳算法，以仿真與實驗結果的差異為目標函數，對加速度曲線進行擬合，識別出了等效激勵參數。劉曉昂[9]采用懸置變形法，在動力總成振動特性實驗的基礎上，結合動力總成剛體模型，識別了等效激勵。總的來說，現有激勵計算或識別方法存在精度不高、過于復雜等不足，并且大多針對偶數缸發動機，對于三缸發動機振動激勵的建模計算研究較少。

本文采用了一種基于多體動力學中拉格朗日乘子法的曲柄連桿機構建模方法，推導了三缸發動機振動激勵的理論表達式。以某三缸發動機動力總成系統為例，計算了其振動激勵，在考慮液壓懸置頻變特性的動力總成位移模型中仿真了各個懸置點的振動加速度響應，與實車測量結果以及通過簡化方法計算激勵進行仿真得到的結果進行了對比驗證。

1 基于多體動力學的發動機激勵計算

1.1 計算假設及坐標系規定

(1)計算假設

在懸置系統開發階段發動機往往設計鎖定，發動機各氣缸內氣體壓力以及曲軸轉角隨時間變化的關系可根據實驗或有限元仿真得到，因此認為這兩個參數的變化規律已知并將其作為計算激勵的輸入。

由于發動機缸體的振動相對于曲柄連桿機構的運動而言較小，模型中忽略了其對于曲柄連桿機構運動特性的影響，計算激勵時假設發動機缸體處于靜止狀態，僅考慮曲柄連桿機構的運動，計算出激勵后再附加到缸體上計算振動響應，屬于單向耦合。

假設動機內部潤滑良好，計算中不考慮主軸承、活塞等處的摩擦損失，也不考慮重力勢能的影響。

(2)坐標系規定

計算激勵時使用的發動機坐標系(Engine Coordinate System, ECS)如圖1所示，坐標系原點O位于遠離飛輪的第一缸軸線與曲軸軸線交點處，x軸沿曲軸軸線方向指向飛輪、變速器一側，z軸沿第一缸軸線方向指向上方，y軸根據右手定則確定。

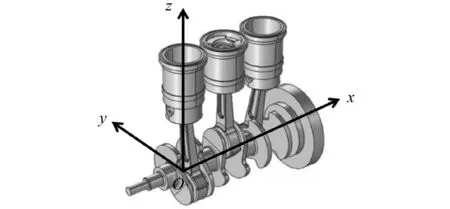
圖1 發動機坐標系示意圖Fig.1 Schematic diagram of engine coordinate system

1.2 曲軸負載力矩計算

將曲柄連桿機構從發動機中分離出來，包括曲軸、連桿、活塞、飛輪、皮帶輪等。本質上，這是一個單自由度系統，但為簡化推導過程，選取第i缸活塞z向位移zpi、第i缸連桿轉角βi及曲軸轉角α共7個廣義坐標(i=1,2,3)，如圖2所示，圖中Cpi表示第i缸活塞質心位置，近似看作位于活塞銷中心處；Ccri表示第i缸連桿質心位置，用ycri及zcri表示其位置；文中i均表示第i缸，i=1,2,3。

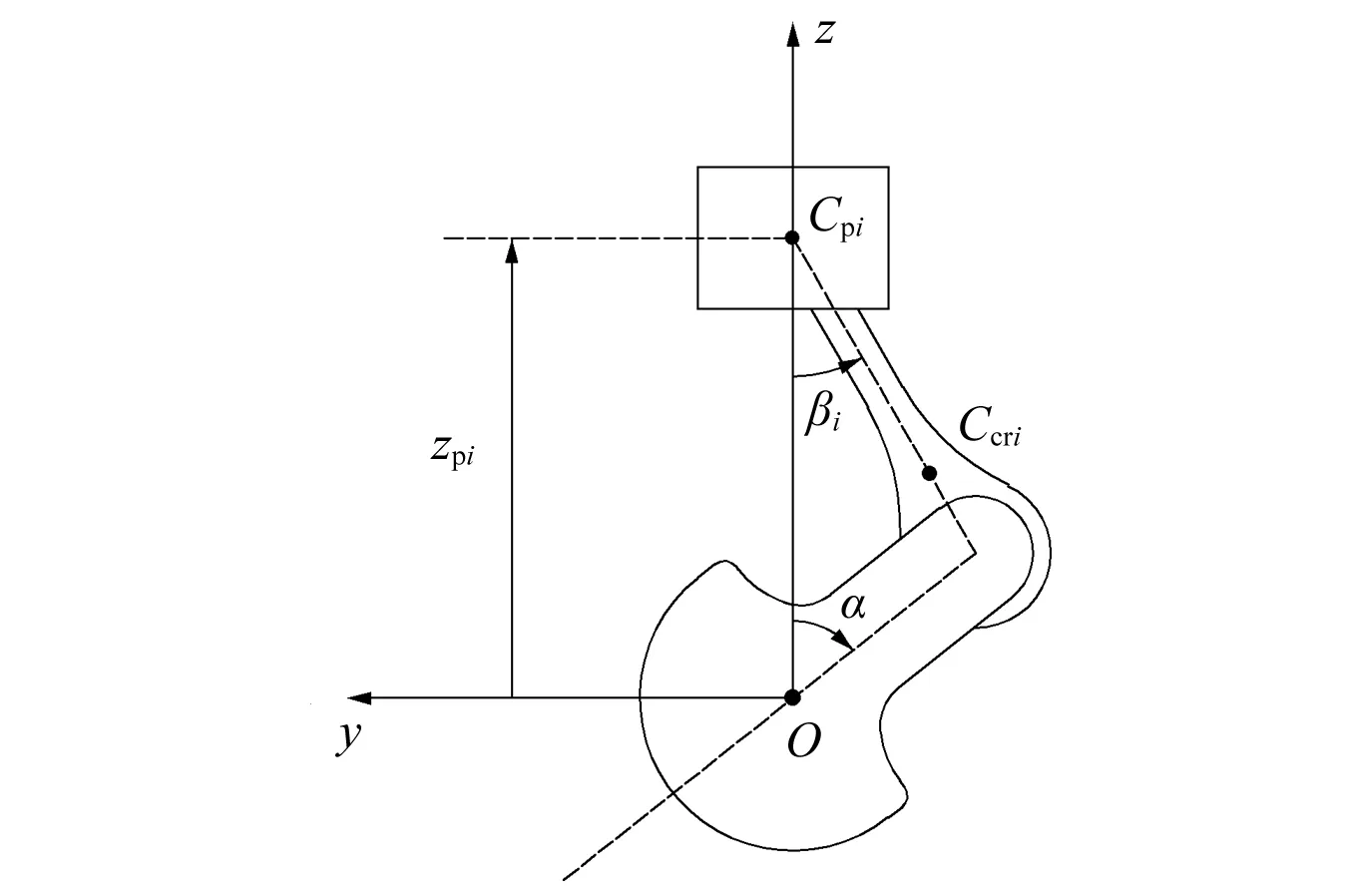
圖2 曲柄連桿機構示意圖Fig.2 Schematic diagram of crank mechanism

由于自動度數小于廣義坐標數，需使用帶乘子的拉格朗日方程[10]

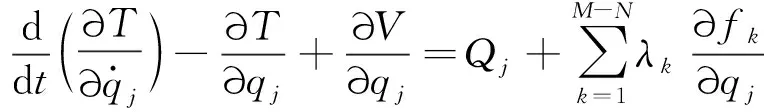
(1)

式中:qj為第j個廣義坐標；T為系統動能；V為系統勢能；Qj為第j個廣義坐標上的作用力；M為廣義坐標數目；N為自由度數；λk為第k個拉格朗日乘子；fk為第k個約束方程；k為約束方程編號。

根據各個氣缸的幾何約束關系，引入6個約束方程

(2)

式中:f1i為第i缸的第1個約束方程；f2i為第i缸的第2個約束方程；r為曲柄半徑；lcr為連桿長度；φi為第i缸與第1缸的曲柄轉角相位差。

系統動能分為三部分：曲軸的轉動動能、活塞直線運動動能以及連桿平面運動動能，可以表示為

(3)

式中:Ics為包含飛輪、皮帶輪的曲軸轉動慣量；mp為活塞質量；mcr為連桿質量；Icr為連桿繞其質心的轉動慣量；l為連桿質心到連桿小頭的距離；vcri為第i缸連桿的質心速度，可表示為

(4)

式中:n1，n2分別為沿y，z軸的單位向量。

由于不考慮重力影響，系統勢能不變，即

V=const

(5)

曲柄連桿機構在各個廣義坐標上受到的外力為

(6)

式中:Tload為曲軸受到的負載力矩；Fgi為第i缸活塞受到的氣體力；pgi為第i缸內的氣體相對壓力；D為活塞直徑。

將式(2)～式(6)代入式(1)中，得到系統的振動微分方程組，包含7個方程

(7)

式中:λ1i為第i缸的第1個拉格朗日乘子；λ2i為第i缸的第2個拉格朗日乘子。

為簡化計算結果，引入一些變量

《說文》中說：“把，握也。從手，巴聲。”可見“把”的本義為“握”“持”，即將物拿在手里，為動詞。后來由“握持”義引申為“把持”“控制”“掌管”義。此時“把”的結構形式為把+NP

(8)

將式(8)代入式(7)并求解方程組，消去拉格朗日乘子，得到曲軸負載力矩表達式為

(9)

式中:I1，I2為曲軸轉角的函數，其表達式為

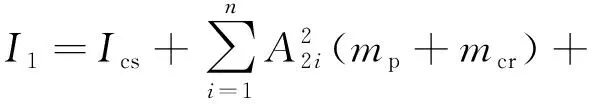
(10)

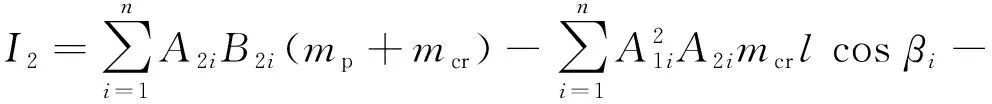
(11)

1.3 慣性力及慣性力矩計算

慣性力及慣性力矩包含兩部分，往復運動部件產生的慣性力及旋轉部件產的慣性力矩。

(1)往復慣性力

由于曲軸往往經過動平衡，其質心位于旋轉軸線上，不會產生往復慣性力，因此，僅考慮活塞以及連桿的往復慣性力。

對于第i缸活塞，僅存在z向慣性力

(12)

對于第i缸連桿，同時存在y向以及z向的慣性力

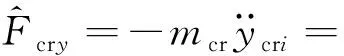
(13)

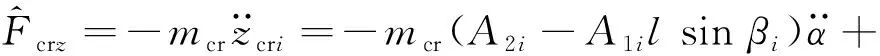
(14)

(2)旋轉慣性力矩

旋轉部件為曲軸和連桿，產生繞x軸的慣性力矩。

對于曲軸

(15)

對于第i缸連桿

(16)

(3)合力及合力矩

將各缸慣性力及慣性力矩平移至坐標系原點，得到總的慣性力及慣性力矩

(17)

(18)

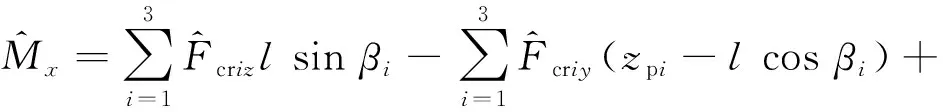
(19)

(20)

(21)

式中:si為第i缸軸線到原點的距離。

1.4 激勵計算結果

將負載力矩與慣性力(矩)按發動機坐標系中的x，y，z平動及轉動方向合成，得到總的激勵，共6個分量

(22)

2 激勵力分析及實驗驗證

為驗證發動機激勵計算的準確性，通常采用的方法有兩種：一是直接法，采用傳遞路徑分析等方法反推激勵；二是間接法，通過對比動力總成懸置點振動響應實測值與仿真值來驗證激勵計算的準確性。直接法復雜繁瑣，而間接法簡單直接，精度能滿足工程需求，故選擇間接法。實驗及仿真對象是帶有變速器的動力總成，在怠速條件下，激勵只來源于發動機，變速器的影響較小，其負載已包含在發動機曲軸負載中。

某三缸發動機、雙離合變速器組成的動力總成系統，采用三點懸置，發動機懸置為液壓懸置，變速器懸置為橡膠懸置，第三點為防扭拉桿。以該系統為例，計算分析了振動激勵，用于動力總成懸置系統的振動特性仿真計算，與實驗測試結果進行了對比。

2.1 三缸發動機振動激勵分析

根據前文的計算方法，編寫MATLAB計算程序計算曲軸負載力矩以及慣性力，圖3列出了主要的計算結果。可以發現，由于考慮了連桿的慣性參數，三缸發動機不僅包含繞y軸的慣性力矩，還包含繞z軸的慣性力矩，二者處于同樣的數量級，而由文獻中的簡化方法計算出的激勵往往不包含繞z軸的不平衡慣性力矩。由于繞x軸的不平衡慣性力矩與負載力矩相比很小，這里不再分析。此外，對于不平衡慣性力，兩種算法的計算結果都很接近0，可以忽略。

(a) 曲軸負載力矩 (b) 繞y軸的慣性力矩 (c) 繞z軸的慣性力矩圖3 主要激勵計算結果Fig.3 Calculation result of typical excitations

2.2 動力總成懸置系統振動仿真

怠速狀態下，動力總成系統的振動激勵只來源于發動機，此時計算出的激勵可以用于動力總成懸置系統的振動仿真。仿真計算時把變速器當作一個剛體附加到了發動機缸體上，共同計算慣性參數后再用于仿真，這是很多文獻中的常見做法，變速器的結構形式和零部件參數對于仿真結果的影響很小，帶上變速器后，氣缸壓力及轉速增加，帶來的負載已包含在曲軸的負載Tload中。

由于本例中懸置安裝方向與整車坐標系(Vehicle Coordinate System, VCS)相同，為方便動力總成懸置系統的建模、描述懸置點的振動情況以及與整車振動評價指標進行比對，建模時采用整車坐標系，原點位于動力總成質心位置，x軸向后，y軸向上，z軸向上。需將根據ECS計算出的激勵轉換為VCS中的激勵再施加，得到的仿真結果也是基于VCS方向。

本文采用的動力總成位移計算模型為6自由度剛體模型，如圖4所示，懸置簡化為無質量的線性三向彈簧阻尼元件，不考慮車身及懸架的影響。該模型應用十分廣泛，根據參考文獻[11]可推導其振動微分方程，這里不再贅述。

本例中第三點懸置為防扭拉桿，可將其視為一個位于防扭拉桿與動力總成連接處的橡膠懸置，采用其襯套的剛度及阻尼[12]。

對于系統中的液壓懸置，其動剛度具有強烈的頻變及幅變特性，為仿真其頻變特性，可以近似將液壓懸置看作一個橡膠懸置附加了液壓系統，橡膠懸置的剛度、阻尼由液壓懸置的橡膠主簧決定，液壓系統將產生一個隨液壓懸置變形量及其頻率變化的液壓力附加在振動激勵中[13]。

考慮了液壓懸置后的仿真系統框圖如圖5所示，在MATLAB/Simulink中搭建相應模型，分別代入本文算法以及根據參考文獻[1-5]中的簡化方法算出的振動激勵，仿真了動力總成懸置系統的振動響應，得到各個懸置點主動端的振動加速度。

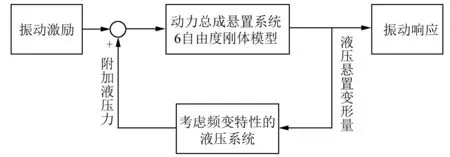
圖5 考慮液壓懸置后的仿真系統框圖Fig.5 Block diagram of simulation program considering hydraulic engine mount

2.3 動力總成懸置系統振動實驗

算例中車型存在怠速抖動問題，對其怠速振動特性進行了實車實驗測量。

實驗采用的數采是德國ZODIAC AEROSPACE公司生產的，型號為DIC24 plus，如圖6所示，采樣頻率設為32 000 Hz。實驗中將3個三向加速度傳感器分別布置在發動機懸置、變速器懸置、防扭拉桿主動端，如圖7所示。

圖6 數據采集儀Fig.6 Data acquisition instrument

(a) 發動機懸置主動端 (b) 變速器懸置主動端

(c) 防扭拉桿主動端圖7 加速度傳感器布置圖Fig.7 Accelerometers’ layout

實驗中，將變速器置于D擋，此時怠速抖動情況最為劇烈，記錄各個懸置上支點即主動端的振動加速度。

圖8列出了發動機懸置及變速器懸置點主動端的振動加速度頻譜，防扭拉桿處仿真中過于簡化，數據參考價值不大，不再考慮。從圖中可以看出，不論使用何種方法，峰值頻率都可以對應。此外，在0～5 Hz內，實測值在有些方向上出現了峰值，是由傳感器測量到的背景噪聲引起的，與系統特性無關。

(a) 發動機懸置主動端x向振動加速度 (b) 發動機懸置主動端y向振動加速度 (c) 發動機懸置主動端z向振動加速度

(d) 變速器懸置主動端x向振動加速度 (e) 變速器懸置主動端y向振動加速度 (f) 變速器懸置主動端z向振動加速度圖8 懸置主動端振動加速度頻域曲線Fig.8 Acceleration results at mount locations of different methods and experiment in frequency domain

D擋怠速時轉速為950 r/min，頻率為15.83 Hz，三缸發動機的主要振動激勵及響應為1階及1.5階，這兩階頻率下的振動加速度相對誤差見表1。

由表1可以看出，在1.5階，兩種算法的準確程度相當，這是由于1.5階激勵主要為氣體燃燒引起的，受到慣性參數的影響很小，兩種算法都是由氣體壓力直接計算激勵，在穩態情況下二者的計算結果很接近。而在1階，考慮了曲柄連桿機構慣性參數后進行仿真得到的結果相比于簡化方法在大多數方向上與實驗結果更加吻合。此外，各個懸置點的z向振動都存在不夠準確的情況，這是由于仿真時僅考慮了液壓懸置的頻變特性，沒有考慮其幅變因素的影響，導致仿真結果出現偏差。在高頻段，兩種方法的計算結果接近，峰值頻率可以對應，但幅值均出現了較大誤差，很可能是液壓懸置的高頻硬化現象引起的，而與激勵計算的準確性無關，從工程應用角度來說，低頻段對于振動加速度均方根值的貢獻更大，高頻段的誤差是可以接受的，若要減小這種誤差，需要考慮液壓懸置硬化現象對仿真進行修正。

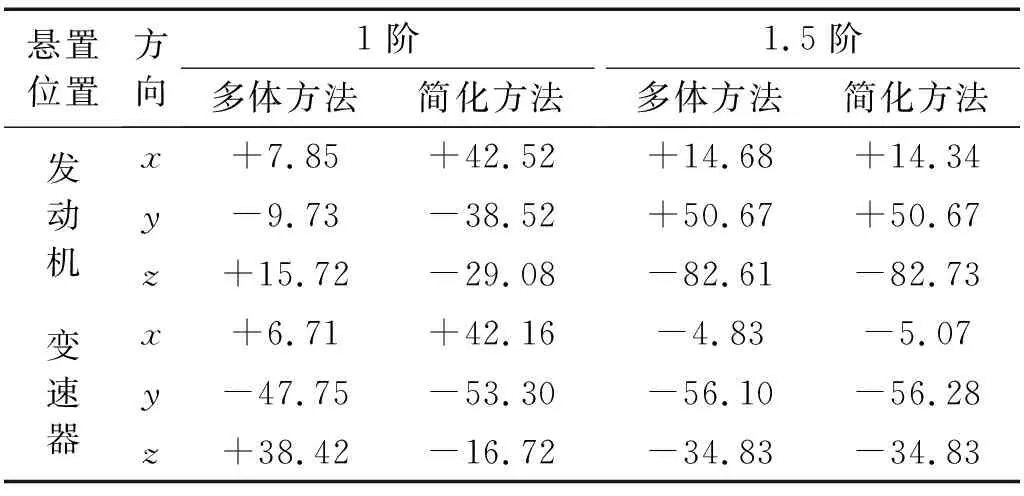
表1 主要階次的振動加速度相對誤差Tab.1 Relative error of accelerationon the main order %

3 結 論

本文采用了一種新的三缸發動機振動激勵建模計算方法，考慮了曲柄連桿機構中連桿等各部件的慣性參數，基于拉格朗日乘子法推導了振動激勵的理論表達式。

以怠速工況下包含某三缸發動機的動力總成系統為例，使用本文方法以及文獻中的簡化方法分別計算了振動激勵，發現相比于簡化方法，考慮了連桿的慣性參數后，多出了繞z軸的不平衡慣性力矩，與繞y軸的慣性力矩數量級相當。繞x軸的慣性力矩與負載力矩相比很小，可以忽略。此外，兩種算法算出的不平衡慣性力合力都近似為0，也可忽略。

將激勵施加到動力總成懸置系統模型中，仿真了各懸置點的振動加速度響應，在怠速工況對該樣車懸置點的振動加速度進行了測量，將仿真結果與實測結果進行了對比，結果表明，考慮連桿等部件的慣性參數后計算出的激勵相比于簡化方法具有更好的準確性，主要體現在各懸置點x,y方向的1階振動加速度上，這主要由于考慮了連桿慣性參數后繞z軸的不平衡慣性力矩未被忽略。

本文的建模計算方法可以推廣到含有任意結構形式的發動機，并且可以用于非穩態工況，如加速過程的仿真，算法中允許各個氣缸的參數存在差異，如各缸氣體壓力差異、點火提前角引起的相位差波動等，更適合應用于要求較高計算準確性的場合，如動力總成懸置系統的優化設計、主動懸置的設計及其控制策略的研究、傳動系統的扭轉減振等。