基于超越閾值模型的低矮房屋實測風壓極值估計方法
黃 鵬, 藍鑫玥, 鐘 奇
(同濟大學 土木工程防災國家重點實驗室,上海 200092)
大量的風洞試驗和現場實測數據表明[1-5],低矮房屋處在大氣邊界層中湍流度較高的底部區域。屋面邊、角、脊等位置受結構本身體型所引起特征湍流的影響,往往會產生幅值很大的風壓“脈沖”。脈動風荷載產生的極值風壓是低矮房屋破壞的重要原因,合理估計脈動風荷載產生的極值風壓是計算低矮房屋風荷載的關鍵,是有效減少低矮房屋風致損壞及毀壞的重要途徑。為此,研究人員基于零值穿越理論與經典極值理論提出了一系列的極值估計方法。
以Davenport[6]為代表的研究人員假定零均值的脈動風壓服從標準高斯分布,根據零值穿越理論提出適用于高斯分布的脈動風壓極值估計方法(下文稱為Davenport法)。然而在高湍流風場的條件下或在風場的流動分離區,風荷載極值分布嚴重偏離高斯假設,采用Davenport法得到的極值估計值與實際結果差別較大。Sadek等[7]在Rice[8]零值穿越理論的基礎上,假設時程的母體符合三參數 Gamma分布,應用Grigoriu[9]的“轉換過程法(Translation Process Approach)”將非高斯風壓時程的概率分布映射成標準高斯分布,由此提出了非高斯過程的極值計算方法(下文稱為Sadek & Simiu法)。映射的標準高斯過程的概率分布函數中的零值穿越率必須由原非高斯時程獲得,該過程對于非高斯較強的時程存在較大的誤差。Quan等[10-12]以經典極值理論為基礎,假定脈動極值風壓時程滿足極值Ⅰ型分布,利用樣本的自相關系數確定母樣本的分段長度,以子段的極值分布規律估算母樣本的極值期望值(下文稱為Quan et al法)。相對于零值穿越理論,該方法在理論上有很大的突破,對極值負壓取得了較為滿意的擬合效果。上述方法均以風洞試驗的風壓數據判斷各種極值估計方法的合理性,而通過現場實測進行合理性驗證的較少,此外,上述方法以零值穿越理論和經典極值理論下的極大值模型(Block Maxima Method, BMM)為基礎。零值穿越理論的核心是假定脈動風壓時程服從高斯分布,而極大值模型存在極值估計準確性受樣本分布影響較大的問題。
因此,本文依托同濟大學土木工程防災國家重點實驗室的風荷載實測基地,以15°屋面坡角低矮房屋在臺風作用下的屋面風壓實測數據為樣本,基于經典極值理論下的超越閾值模型,提出一種以廣義Pareto分布為擬合分布的脈動風壓極值估計方法。首先確定閾值的上下限,將閾值等分為若干區間,并計算每一區間經驗平均超額分布函數的斜率,以擬合殘差平方和最小的方式選擇合理的閾值區間,且將該區間第一個值作為最優閾值。本文分析了分段數的不同對擬合結果的影響,同時,探討了本文方法在不同閾值選取方式中的優越性。此外,以10 min標準時距下觀察風壓極值的平均值作為標準極值,比較了本文方法所得極值估計值與標準極值的誤差,并將本文方法與常用極值估計方法進行對比。
1 實測概況
實測基地依托同濟大學土木工程防災國家重點實驗室,位于上海浦東國際機場附近沿海入海口區域,包括一棟屋面坡角可連續調節的足尺實測房,一座高約10 m和一座高約40 m的格構式測風塔[13]。其中,低矮房屋實測房長約10 m,寬約6 m,建筑檐口高度為8 m,代表了大部分村鎮房屋的外形特征,屋面坡角可從0°~35°自由調節,滿足對一般低矮房屋風荷載研究的需要。風壓采集系統主要布置在屋面,其測點布置圖如圖1所示。

圖1 浦東實測基地概況Fig.1 Pudong experimental base
本文使用實測風速樣本為2016年第16號強臺風“馬勒卡”,其中心附近最大風力有14級(45 m/s)。下節將基于同濟大學實測基地所采集到的在強臺風“馬勒卡”影響下低矮房屋15°坡角屋面風壓結果,對典型位置關鍵測點的脈動風壓時程進行分析。
2 脈動風壓特性
結合“馬勒卡”影響上海的實際時間,本文所選取的樣本風速時程為2016年9月17日23時后48 h內實測基地10 m高度處的風速數據。
2.1 脈動風壓分布特性
根據前人的研究成果,低矮房屋鈍體形態明顯,風荷載作用在低矮房屋的同時會形成明顯的沖擊、分離及旋渦脫落等特征湍流。因此,本文選取迎風面前端角部處測點74、背風面靠近屋脊位置測點36、背風面靠近山墻測點29及背風面后端中間位置測點6這4個具有代表性的測點進行脈動風壓系數的研究。圖2給出了典型測點在臺風“馬勒卡”影響下,平均風速為12.16~15.32 m/s湍流強度為0.35、湍流積分尺度為52 m、屋面坡度為15°時脈動風壓系數隨風向角的變化。
從圖2 可以看出,當風向角在0°~50°內,背風面靠近屋脊位置測點36、背風面靠近山墻測點29的脈動風壓系數隨著風向角的增大而增大,且在風向角為30°~35°時數值增大速率較大。背風面后端中間位置測點6的脈動風壓系數穩定在0.2~0.3,迎風面前端角部處測點74的脈動風壓系數穩定在0.7~0.8。
可見,當風向角在0°~35°內,隨著風向角度的增大,屋脊對來流的氣動分離作用對背風面靠近屋脊位置和背風面靠近山墻區域屋面測點的脈動風壓系數的影響逐漸加強,而整個屋面其他區域的脈動風壓系數維持穩定。
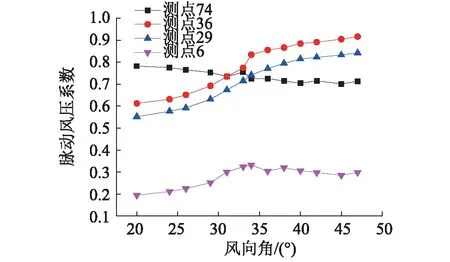
圖2 關鍵測點脈動風壓系數隨風向角的變化Fig.2 Curve of fluctuating wind pressure coefficient with wind direction angle at critical points
2.2 脈動風壓概率特性
研究表明[14-17],屋面風壓具有非高斯性,特別是邊、角、脊等典型位置的風壓存在幅值較大的“脈沖”(見圖3(a)),當然,屋面部分區域測點的非高斯性并不明顯(見圖3(b))。
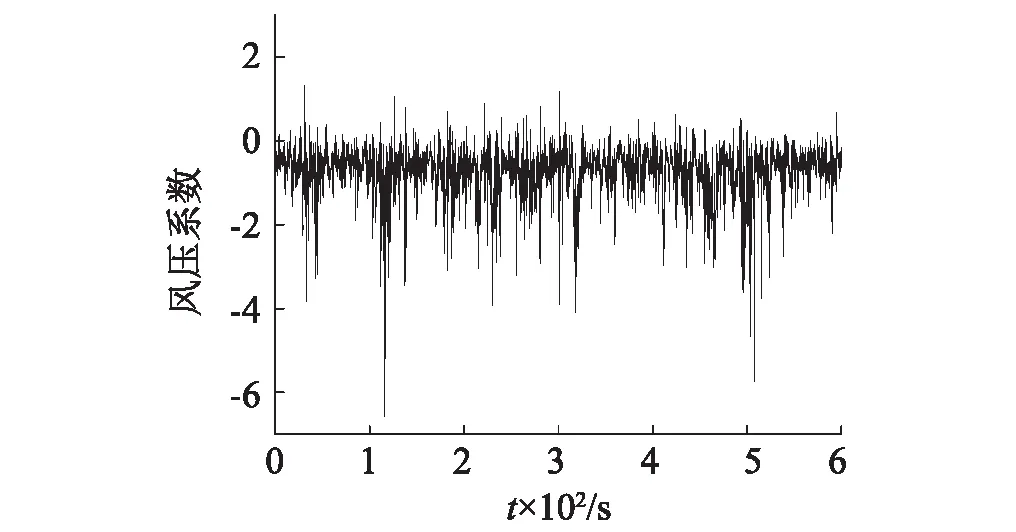
(a)特征湍流作用區域測點
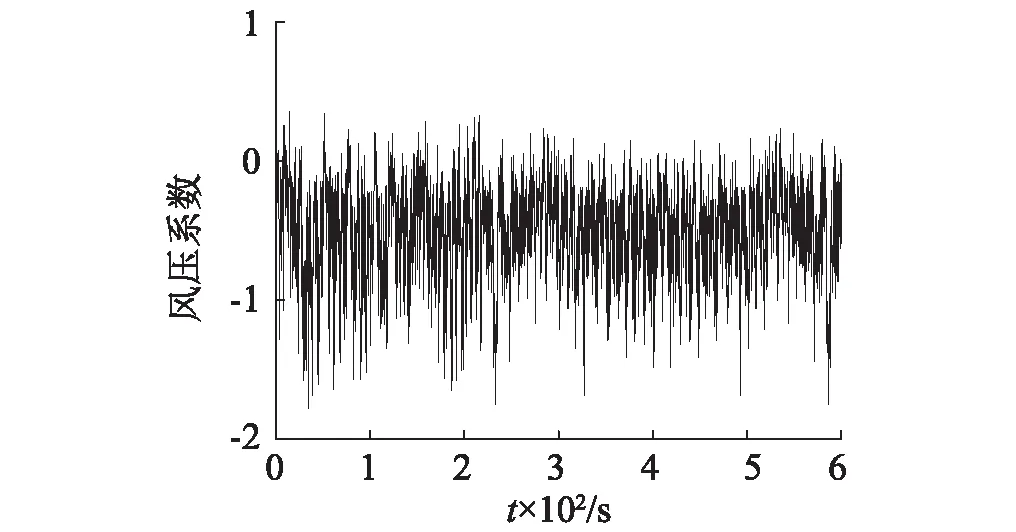
(b) 非特征湍流作用區域測點圖3 實測風壓系數時程Fig.3 Measured wind pressure coefficient time history
為直觀分析低矮房屋屋面風壓的非高斯性及概率分布特性,本文對10 min平均風速為13.56 m/s、平均風向角為39°的屋面關鍵測點實測脈動風壓時程的概率分布采用Gauss分布、Lognormal分布、GEV分布與Gamma分布進行擬合,擬合結果見圖4。
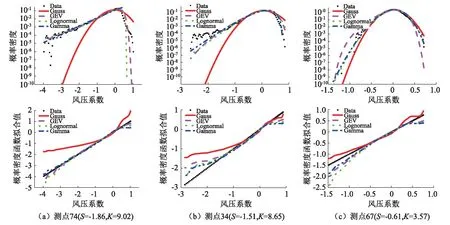
圖4 關鍵測點風壓系數時程概率分布特性及擬合效果Fig.4 Probability distribution characteristics and fitting effect of wind pressure coefficient time histories at critical points
從圖4可以看到,測點74和測點34的概率分布呈現較為明顯的負偏態,且均不服從Gauss分布、Gamma分布、Lognormal分布與GEV分布。在風壓系數概率密度曲線的尾部即極端值區域的擬合效果并不理想。而測點67的風壓實測數據與高斯分布擬合值相對誤差不大,擬合效果優于測點74與測點34。其原因在于,測點74與測點34位于受特征湍流影響的邊、角、脊位置,這些位置在旋渦脫落等湍流效應影響下,偏度系數與峰度系數絕對值較大(測點74的偏度系數為-1.82、峰度系數為8.16,測點34的偏度系數為-1.43、峰度系數為5.86),風壓具有較強的非高斯性,采用Gauss分布(標準高斯過程的偏度系數范圍為-0.5~0.5,峰度系數范圍為2.5~3.5)描述風壓系數的概率特性是不合適的。而測點67位于迎風屋面中央,受特征湍流的影響小,風壓基本圍繞均值對稱分布,非高斯性不顯著,但Gauss分布對風壓極值的擬合精度仍然不高。
由此可見,風壓系數無法采用單一確定性函數較準確地描述其概率特性,風壓極值的合理估計是比較困難的。以下采用基于經典極值理論下超越閾值模型的極值估計方法估計實測風壓極值。
3 風壓極值估計方法
3.1 超越閾值模型及廣義Pareto分布
超越閾值模型以超過某一閾值的數據作為研究對象,有效地利用了有限的極端觀察值,被廣泛應用于極值分析、可靠性研究等領域。超越閾值模型分析超出閾值的數據(超閾值)的概率特性,即該模型主要針對母體樣本分布的尾部區域。
選擇適當的閾值,是準確估計廣義Pareto分布形狀參數與尺度參數的前提,也是正確分析數據的關鍵。研究人員發現,極值估計值對閾值非常敏感:閾值太
大,則樣本數據容量有限,樣本不具有代表性;閾值太小,則樣本數據無法滿足廣義Pareto分布的要求,所得極值并不準確。目前,選取閾值的方法主要分為圖解法和計算法兩大類,計算法以峰度法及漸進均方誤差法為代表。但上述兩種方法計算效率較低,存在一定的局限性。
研究發現,超閾值服從廣義Pareto分布。本節對廣義Pareto分布進行介紹。
廣義Pareto分布的概率分布表達式為
(1)
式中:μ∈R為位置參數;ξ∈R為形狀參數;σ>0為尺度參數。
總體分位數函數為
(2)
極大似然估計是漸近正態分布的,且所得參數比較穩定,本文采用極大似然估計方法對形狀參數ξ和尺度參數σ進行估計,具體方法如下:
超閾值的廣義Pareto分布的概率密度函數為
(3)
式中:u為閾值。
那么對數似然函數為
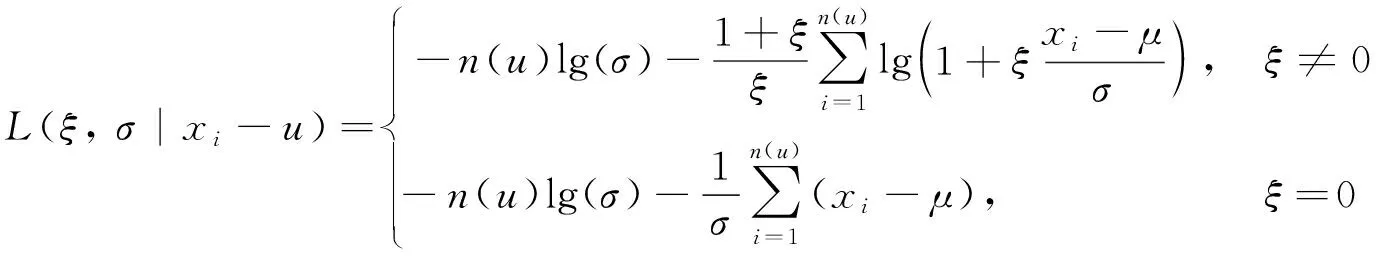
(4)
分別對ξ和σ求偏導并令其等于0,可得
(5)
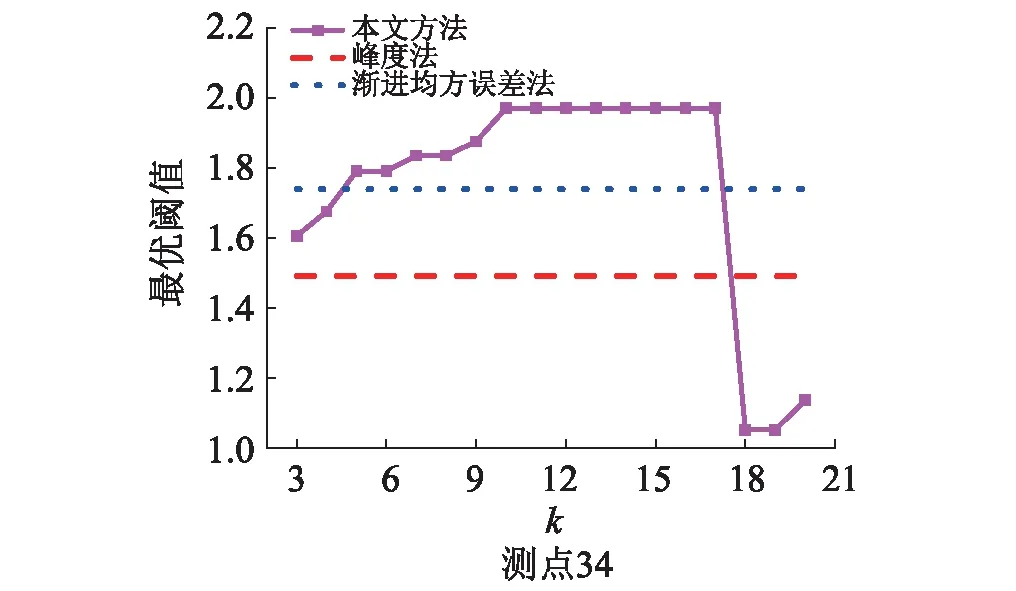
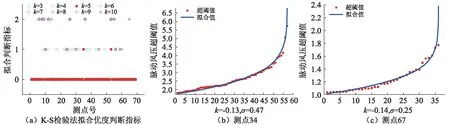
求解上述方程即可得到廣義Pareto分布中參數ξ和σ的估計值。對于0 (6) 平均超額分布函數為超過閾值的樣本均值,對于廣義Pareto分布而言,其相應的表達式為 (7) 對于離散數據,可以定義經驗平均超額分布函數為 (8) 本文方法基于兩個原理。首先,若超閾值服從廣義Pareto分布,則平均超額分布函數可描述為閾值的線性函數,如式(7)所示;其次,現有的經驗平均超額分布函數圖法(計算法)通過構造曲線肉眼選擇使平均超額分布函數近似線性且斜率為正的閾值u0為合理閾值,屬于定性判斷,憑直覺和經驗,存在主觀性明顯的缺陷,有時受樣本數據結構影響甚至無法適用。本文提出以擬合殘差平方和最小的方式對經驗平均超額分布函數圖法的合理改進,直接給出最優閾值u的大小,提高選取閾值的穩定性。 為了便于理解和采用,將此方法的計算步驟總結如下: 步驟1 根據浦東實測基地采集到的脈動風壓時程數據,選擇合適的閾值下限u1和上限un; 步驟2 將閾值區間[u1,un]進行等分,以k(k 步驟3 計算每一組數據中的第一個點和最后一個點連成直線的斜率,由定義有 (9) 步驟4 設q(li)為每一組數據對直線li的擬合殘差平方和,由定義有 (10) 步驟5 選取擬合殘差值最小的那組數據,并在其中選取第一個點的橫坐標對應的脈動風壓大小作為最優閾值; 從擬合殘差公式得到的參數轉換關系式(10)可以看出,分段數(n-k+1)越大,每段中的數據越少,則越能反映經驗平均超額分布與閾值之間線性關系,即所得到的擬合殘差值越具有說服力。但是隨著分段數的增大,則相鄰段子樣本之間的相關性較強,且明顯地增大計算時間,降低計算效率。因此,有必要研究最優閾值與k值之間的相互關系。 (1)以現有方法的最優閾值為標準 圖5給出了屋面15°坡角低矮房屋屋面典型測點脈動風壓分別采用本文方法、峰度法及漸進均方誤差法得到的最優閾值與k的關系曲線。本文對各測點10 min標準時距下的脈動風壓時程樣本采用本文方法將閾值區間分別按3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20個數據為一組等分得到最優閾值,并以峰度法及漸進均方誤差法下的最優閾值作為參考。由圖5可以看出,當k的值為5時,利用本方法得到的最優閾值與漸進均方誤差法得到的最優閾值比較接近。更多測點的計算結果同樣也證實了這一結論的正確性。 (a)測點34 (b)測點67圖5 不同閾值選擇方式最優閾值的比較Fig.5 Comparison of different threshold selection methods (2)以K-S檢驗法作為擬合優度的評判標準 為進一步確定本文方法的合理性,本文選取Kolmogorov-Smirnov檢驗法作為判斷超閾值是否服從廣義Pareto分布的標準,并引入擬合優度判斷指標來合理區分不同情況。其值為0時表明在顯著型水平0.05下接受原假設,即認為超閾值服從廣義Pareto分布;其值為1時表明在顯著型水平0.05下拒絕原假設,即認為超閾值并不服從廣義Pareto分布;其值為2時表明由于閾值較高,超閾值樣本數量不足以與廣義Pareto分布進行比較。 由Pickands[18]的理論研究成果可知,若最大值Mn近似服從廣義極值分布,則超閾值X|X-u與超出量X-u近似服從廣義Pareto分布,因此,可利用GPD(Generalized Pareto Distribution)擬合超閾值,從而利用超閾值分布求總體分布函數。 從圖6中可以看出,當k=5時低矮房屋屋面各測點基于本文方法得到的超閾值與廣義Pareto分布擬合程度較好,可以認為超閾值服從廣義Pareto分布。更多的擬合結果同樣也證實了這一結論的正確性。 圖6 超閾值與廣義Pareto分布的擬合效果Fig.6 Fitting effect of data beyond threshold and generalized Pareto distribution 峰度法、漸進均方誤差法是目前較為常用的超越閾值模型極值估計方法。本文采用標準時距(臺風工況采用10 min)下脈動風壓時程的觀察極值作為標準極值,將上述兩種方法及本文方法所得脈動風壓極值估計值與標準極值進行比較,以標準誤差率均值來衡量屋面關鍵測點在不同閾值選取方式下估計極值與標準極值之間的接近程度。 標準誤差率平均值的表達式為 (11) 式中:M為標準時距樣本數;N為所包含測點總數。 圖7表示的是臺風作用下超越閾值模型不同閾值選取方式所得極值估計值與低矮房屋屋面實測脈動風壓的標準極值的比較。從誤差率均值的角度而言,漸進均方誤差法與本文方法所選取的閾值比較可信,而峰度法得到的閾值其估計結果與真實值誤差率在-0.1~-0.5,并不穩定。而漸進均方誤差法由于采用最小二乘法估計參數值,因此,在計算效率上比本文方法低得多,在工程及風洞試驗的數據處理時其優越性并不突出。 基于零值穿越理論的Davenport法、Sadek & Simiu法以及基于經典極值理論的Quan et al法是目前較為常用的風壓極值計算方法。本文用上述方法得到屋面測點脈動風壓極值估計值,并與標準極值進行比較。 本文提出以擬合殘差平方和最小的方法對經驗平均超額分布函數圖法進行改進,可直接得到最優閾值u,并將超閾值與廣義Pareto分布進行擬合,以擬合廣義Pareto分布的期望值作為估計極值,并與標準極值進行比較。 (a)估計極值與標準極值 (b)誤差率均值圖7 不同閾值選取方式的比較Fig.7 Comparison of different threshold selection methods 對于標準極值的選取,陶玲等[19-20]將多次采樣獲得的樣本極大值的均值作為標準極值用于比較各種極值估計方法的準確性,并論證了選取均值作為比較標準是偏于保守的。本文根據上述結論截取浦東實測基地實測房屋面2 h脈動風壓時程數據,以10 min為標準時距,將12個標準時距中的觀察極值的期望值作為標準極值,以標準誤差率均值來考察不同方法估計極值的準確性。 圖8表示臺風作用下常用極值估計方法所得極值估計值與低矮房屋屋面實測脈動風壓的標準極值的比較。從圖8中可知,Davenport法所給出的極值估計結果(絕對值)比標準極值小,誤差均值基本集中在-0.4~-0.6,即采用Davenport法所擬合得到的脈動風壓極值會極大地低估風壓對結構的作用,特別對于極端值區域偏離程度更大;Sadek & Simiu法的極值估計效果優于Davenport法,誤差均值基本保持在-0.4~0.1,離散程度較大,表明極值估計的效果不太好。Quan et al法給出的極值估計值結果較均勻地分布在標準極值上下,擬合結果較好,但離散程度仍較大。而本文方法離散程度最小,受來流擾動的影響較小,且極值估計值與標準極值誤差率基本控制在5%以內。 表1給出了低矮房屋屋面特征湍流影響區域(迎風面前端角部、背風面靠近屋脊角部)關鍵測點標準極值與估計極值及其誤差率。可見,Davenport法由于假定風壓系數服從標準高斯分布,與實測風壓系數的概率分布相差較大,因此,非高斯性較強區域風壓系數極值估計值的誤差也很大。Sadek & Simiu法以及Quan et al法極值估計結果相比Davenport法有較大改善,但對于非高斯性較強的風壓系數極值估計仍不太理想。 (a)標準極值與估計極值 (b)誤差率均值圖8 常用極值估計方法的比較Fig.8 Comparison of common extreme value estimation methods 本文方法對風壓較大區域的極值估計結果與實測值的誤差率均值控制在-5%以內,因此,采用本文方法對低矮房屋屋面風壓極值估計是可行的、有效的。 表1 標準極值與估計極值的誤差Tab.1 Error of standard extreme values and estimated extreme values 通過對臺風作用下位于上海浦東國際機場附近實測基地的實測房15°坡角屋面脈動風壓的研究,采用極值理論下的超越閾值模型,并以廣義Pareto分布作為風壓極值的擬合分布合理估計屋面風壓極值,可得到以下結論: (1)Davenport法對脈動風壓極值的估計結果誤差較大,誤差率均值達到40%~60%,因此,采用Davenport法作為極值估計方法會顯著低估脈動風壓極值對結構的影響;而Sadek & Simiu法對于非高斯性較強的時程所得極值估計值存在較大誤差;Quan et al法雖然在一定程度上減小估計極值與標準極值的誤差,但方法本身并不穩定,部分測點的誤差率仍在10%以上。 (2)本文方法是對超越閾值模型的有益嘗試,以廣義Pareto分布作為風壓極值的擬合分布得到的極值估計值與標準極值誤差率控制在5%以內,特別對極值風壓較大區域的估計結果較為理想,體現了該方法在現場實測條件下對屋面脈動風壓極值估計準確性。 (3)超越閾值模型對閾值比較敏感,基于不同閾值選取方式得到的極值估計值相差極大。從誤差率均值的角度分析,漸進均方誤差法與本文方法所得到的最優閾值比較可信,而峰度法所得到的最優閾值無法作為超越閾值模型的合理閾值。3.2 本文風壓極值估計步驟
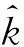
3.3 分段數的確定

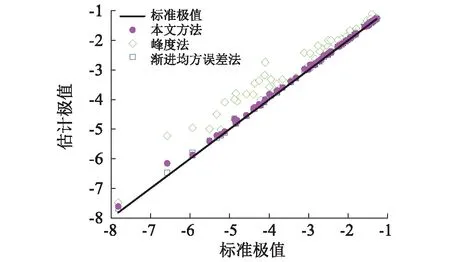
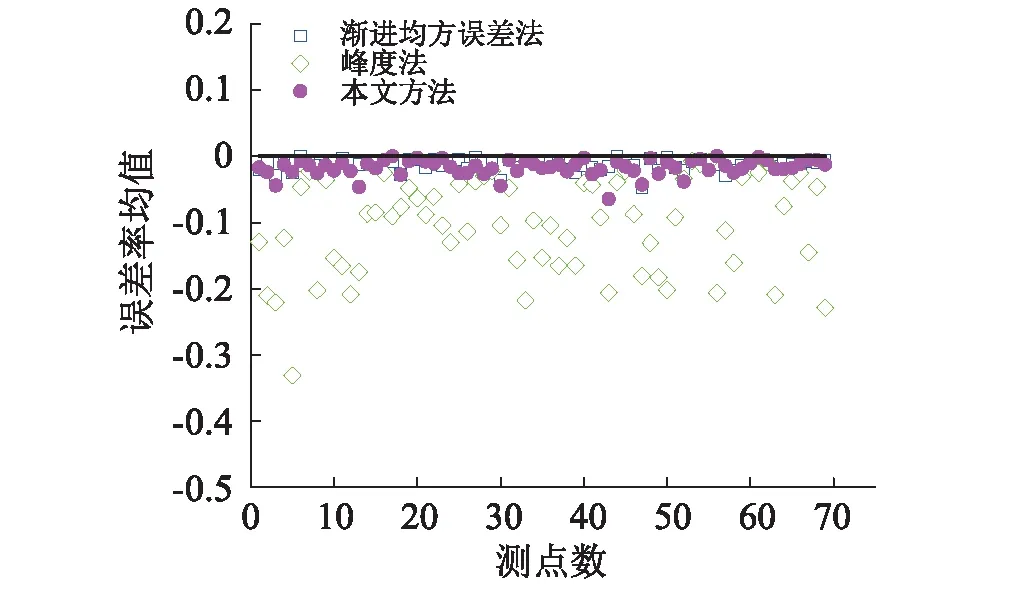
3.4 不同閾值選取方式的比較

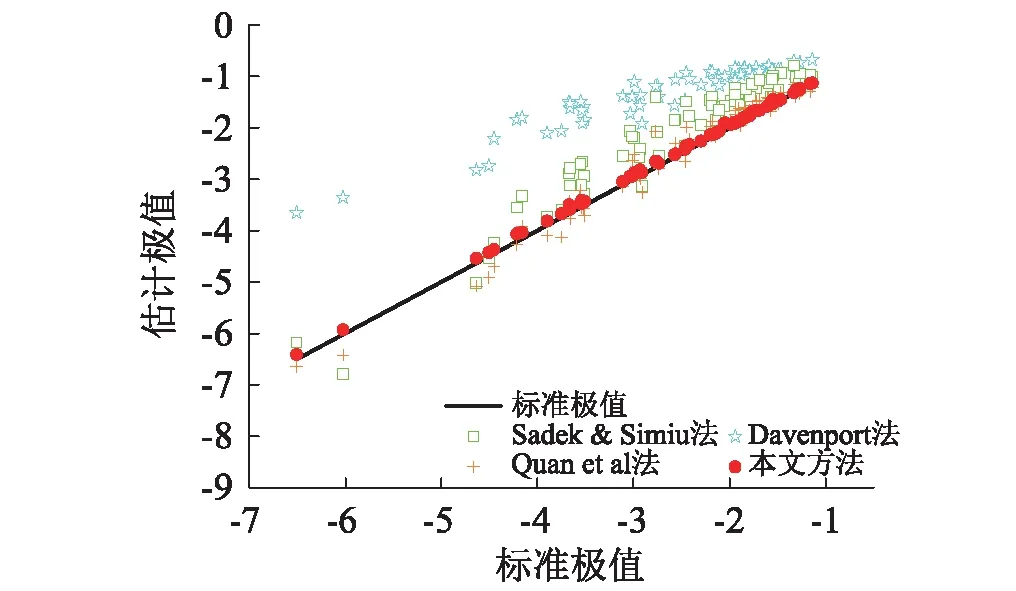
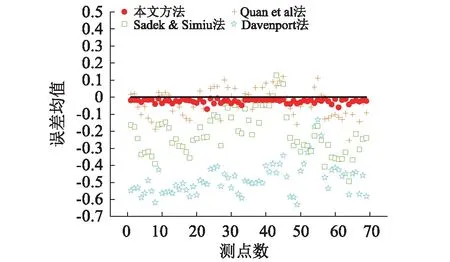
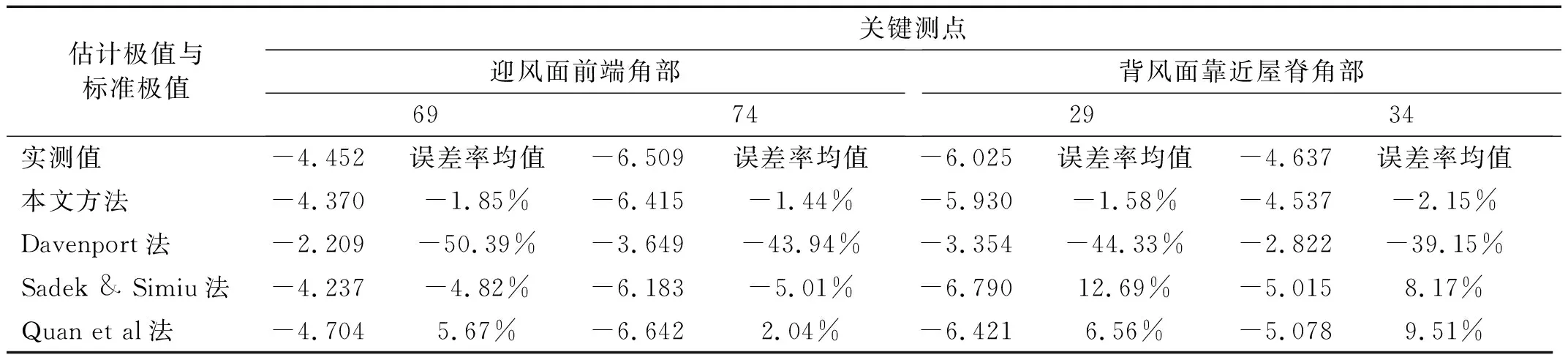
3.5 不同極值估計方法的比較
4 結 論

