基于全周期電流包絡線開關磁阻電機無位置傳感器技術

張磊 劉闖 韓守義

摘?要：針對開關磁阻電機在低速運行狀況下位置估計困難的問題，依據轉子位置信號與電感曲線之間關系，提出一種全周期脈沖電流峰值包絡線的無位置傳感器技術。導通區域利用固定轉波時間的斬波控制方式，非導通區域進行注入高頻脈沖，兩個區域里分別檢測出脈沖電流的峰值，通過數學擬合得到全周期脈沖電流包絡線與電機轉子位置角之間的數學模型，再通過簡易的邏輯比較模塊即可得到電機轉子位置信號，再根據轉子位置信號之間的夾角估算出電機轉速和轉子位置角度。所提方法由于三相電流包絡線交接點在電感上升和下降過程中，電感變化率大，所以不同脈沖下的電流峰值變化大，從而提高了微處理器處理精度，且不需要預先設置脈沖電流閥值，算法簡單，容易實現。最后通過仿真和實驗，驗證了所提方法的正確性和可行性。

關鍵詞：?開關磁阻電機;全周期包絡線;位置估計;斬波控制;脈沖注入

DOI：10.15938/j.emc.2019.11.014

中圖分類號：TM?351

文獻標志碼：A

文章編號：1007-449X（2019）11-0109-09

收稿日期：?2017-08-20

基金項目：國家自然科學基金（51377076）;江蘇省自然科學基金（BK20151574）

作者簡介：張?磊（1974—），男，博士，副教授，研究方向為開關磁阻電機無位置傳感器技術;

劉?闖（1973—），男，博士，教授，博士生導師，研究方向為特種電機及控制、新能源技術;

韓守義（1982—），男，博士研究生，講師，研究方向為多相開關磁阻電機及控制技術。

通信作者：張?磊

Sensorless?of?switched?reluctance?motor?drives?based?on?full?cycle?current?envelope

ZHANG?Lei1，?LIU?Chuang2?，?HAN?Shouyi2

（1.School?of?Electronic?Engineering，?Nanjing?Xiaozhuang?University，Nanjing?211171，China;

2.College?of?Automation?Engineering，?Nanjing?University?of?Aeronautics?and?Astronautics，?Nanjing?210016，China）

Abstract：

In?order?to?solve?the?difficulty?of?sensorless?low?speed?operation?of?switched?reluctance?motor，according?to?the?relationship?between?the?rotor?position?signal?and?the?inductance?curve?and?the?peak?value?of?the?pulse?current?for?the?switched?reluctance?motor，?a?new?sensorless?technique?was?presented?using?the?full?cycle?pulse?current?peak?envelope.?Using?the?chopper?control?mode?in?the?conducting?region，?and?using?the?high?frequency?pulse?injection?in?the?nonconducting?region，?and?the?peak?value?of?the?pulse?current?was?detected?in?the?two?regions，?the?mathematical?model?between?peak?envelope?of?pulse?current?and?rotor?position?was?obtained?by?fitting.?The?position?signal?was?estimated?by?means?of?using?a?simple?logic?comparison?module，?and?the?motor?speed?and?rotor?position?angle?were?estimated?.?Because?the?envelope?intersection?point?is?not?in?the?maximum?and?minimum?inductance?regions，?the?position?estimation?error?is?small，and?also?need?not?set?the?pulse?current?threshold.?The?algorithm?is?simple?and?easy?to?implement.?The?experiments?and?simulation?results?demonstrate?the?feasibility?and?the?practicality?of?the?proposed?method.

Keywords：switched?reluctance?motors;?full?cycle?envelope;?sensorless;?chopper?control;?pulse?injection

0?引?言

開關磁阻電機（switched?reluctance?motor，SRM）是定轉子為齒槽結構，定子齒上饒通電線圈，轉子齒上無繞組，也無永磁材料，所以結構簡單、堅固、高容錯性等特點，非常適合在礦井傳動系統、航空、電動汽車、紡織等領域[1-4]。但在開關磁阻電機調速系統中，控制系統需要有準確的轉子位置信號，而轉子位置信號是要安裝位置傳感器，這樣會增加了系統的復雜性，如果位置傳感器發生故障，系統運行會混亂，降低了系統的可靠性，因此SRM無位置傳感器技術得到國內外很多學者的廣泛研究。

開關磁阻電機位置估計主要脈沖注入、電流梯度、電感模型、簡化磁鏈等方法，脈沖注入法是低速狀態下位置估計的常用方法，文獻[5]針對三相SRM傳動系統，同時對兩非導通相注入高頻電壓脈沖信號，比較脈沖電流峰值大小估計換相位置，該方法不需要增加硬件，但將電機電感理想為分段線性電感，所以換相點估計精度不高，也可能產生負轉矩現象。文獻[6]采用電流峰值與預設的電流閥值比較估計轉子位置，對某一非工作相注入高頻脈沖，利用均值采樣數學方法計算出脈沖電流峰值，針對母線電壓波動影響電流閥值的問題，文獻通過增加修正模塊，提高了峰值的精度，該方法峰值計算過程較復雜。文獻[7]針對分塊SRM提出了一種改進型脈沖注入方法，對非導通相注入脈沖電壓，與傳統的脈沖注入不同的是通入電壓時間是逐漸增大，這樣會減少脈沖電流峰值微小而影響到位置估計精度，但脈寬變大會使電機產生反向轉矩，降低起動效率。文獻[8]在PWM控制方式下，比較相鄰PWM信號下的電流大小，計算其電流峰值和時間，根據微處理器記錄的實時計數值與開通角、關斷角時刻的脈沖數比較，估計下一相的開通角和關斷角。文獻[9]對非導通相注入高頻脈沖，計算出脈沖電流上升的斜率和脈沖電流下降的斜率，由于脈沖電流上升的斜率與下降斜率差的包絡線與相電感曲線相同，所以文獻通過比較三相斜率差的包絡線實現轉子位置的估計，該方法避開了反電動勢的影響，提高了位置估計的精度。文獻[10]對非導通相注入高頻脈沖，導通相采用PWM控制，分別采集電流上升和下降脈沖電流斜率，由脈沖電流斜率差間接估算電機電感，再通過電感分區和預設電感閥值來估計起動相，該方法脈沖電流峰值的提取比計算電感信息容易。文獻[11]根據電感與轉子位置信號之間的邏輯關系，將電感分區，通過比較三相電感大小估計轉子位置信號。文獻[12]將電機的電感模式和電壓平衡方程相結合，通過數學手段推到出位置估計數學模型，該方法雖然沒有增加硬件系統，但沒有考慮互感對電感的影響。文獻[13]基于非線性電感模型，分別針對單相勵磁和雙相勵磁兩種狀態下進行位置估計，由于雙相勵磁產生互感，文獻采用了磁鏈差值計算，減小相間互感對位置估計的影響，提高了位置估計精度。文獻[14]將電機電感模型轉為復平面，利用電感向量合成規律，分析矢量角與轉子位置角度之間的關系實現了位置估計，該方法優點是不需要增加硬件也不需要測量電機磁鏈。文獻[12]將電感曲線進行分區，最大和最小電感獨立作為一個區域，根據分區規律預設高低兩個電流閥值，通過脈沖電流峰值與閥值比較獲取換相信號，該方法避免了因電感最大和最小區域電感變化微小而影響到位置估計精度的問題，但雙電流閥值的選擇較復雜。

本文提出一種基于全周期脈沖電流包絡線的無位置傳感器方法。在導通區域利用斬波控制方式，非導通區域進行注入高頻脈沖，在兩個區域里分別檢測出脈沖電流的峰值，通過數學方法處理，整合為全電感周期的脈沖電流包絡線，再通過邏輯比較即可估計出電機轉子位置信號，該算法簡單、實用，并通過實驗進行了驗證。

1?脈沖注入原理

開關磁阻電機不對稱半橋功率變換器，非常方便脈沖注入方法的實現，當給電機的相繞組注入高頻電壓信號時，由于注入的電壓很小，所以可以忽略電機飽和相間互感，電機的電壓平衡方程式為

uk=Rkik+Lk（θ）dikdt+ikωdLk（θ）dθ。（1）

式中：uk為第k相繞組的端電壓;Rk為第k相繞組的電阻;ik為第k相繞組的相電流;Lk為第k相相電感;ω為電機的轉速;θ為電機的轉子位置角;k=1，2，…，m，m為電機相數。

在電機低速情況下，相電流和電機轉速都很小，式（1）中相繞組電壓和旋轉電動勢Rkik、ikωdLk（θ）dθ可以忽略，則式（1）可簡化為

uk≈Lk（θ）dikdt。（2）

即

Lk（θ）≈UkΔTipeak。（3）

式中：ipeak為脈沖響應電流，從式（3）可以看出，當端電壓Uk和注入的高頻脈沖開通時間ΔT固定時，電機的相電感Lk（θ）和脈沖電流峰值ipeak成反比（圖1所示），電機的相電感Lk（θ）包含了轉子位置角θ信息，因此可以通過檢測脈沖響應電流，解算出轉子的位置信息。

2?全周期包絡線位置估計策略

傳統的脈沖注入方法是對非導通相注入高頻脈沖信號，需要預設電流閥值，僅適合于單拍運行控制，本文在其基礎上對電流峰值包絡線的提取進行了改進，結合脈沖注入和斬波控制，提出了全周期脈沖包絡線的無位置傳感器技術。

2.1?全周期脈沖電流包絡線提取

一個電感周期分2個過程，第一個過程為電感下降區域，其過程為非導通區域，在此區域注入高頻脈沖信號，第二個過程為電感上升區域，其過程為導通區域，其區域采用固定斬波時間Δt的斬波控制方式，如圖2所示。

1）脈沖注入過程：PWM1為注入的高頻脈沖，Δton為開通時間，脈沖電流從零開始上升，i1為脈沖電流峰值，即脈沖電流的變化量為i1，所以式（3）變為

Lk（θ）≈UkΔtoni1。（4）

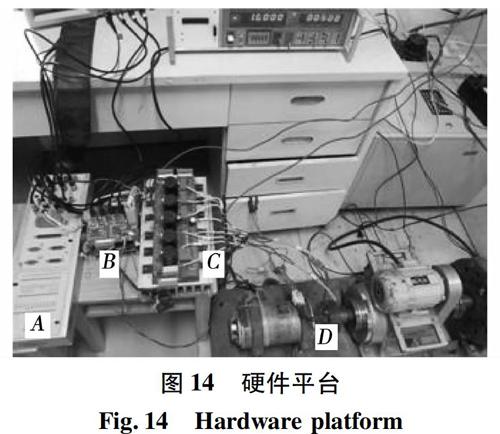
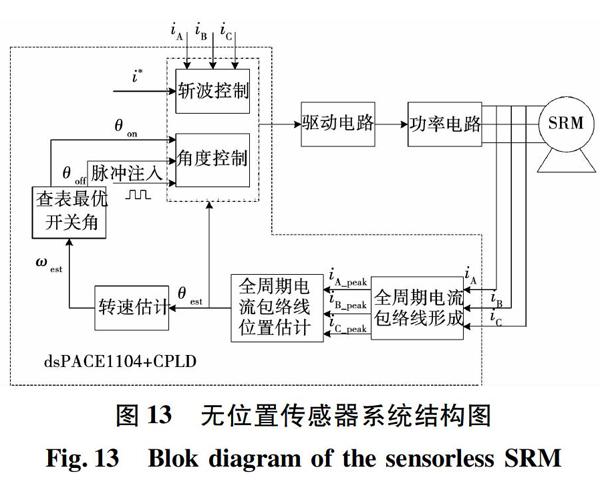
2）斬波控制過程：在固定斬波時間Δt的斬波控制方式下，設置一個斬波限i，當斬波限電流i大于相電流i，斬波PWM2信號為1，開通開關管，相電流繼續上升，當i

Lk（θ）≈UkΔtoffi-i2。（5）

對比式（4）和式（5），如果PWM1中的Δton與PWM2中的Δtoff相等，則兩個過程中的電流變化量相等，在PWM1下降沿時刻采集脈沖電流峰值，再經過擬合處理，得到脈沖電流包絡線i1，在PWM1上升沿時刻采集斬波控制期間的脈沖電流，同樣經過擬合處理，得到脈沖電流包絡線i2。

根據脈沖注入法原理，在相等的時間里，脈沖電流的峰值與電感成發比，所以只要保證Δton和Δtoff相等，i1和i2電流的峰值反應電感的變化情況，與電感成反比。按照數學幾何知識，包絡線i2關于1/2i對稱可得到包絡線i3，再將i1與i3包絡線通過“異或”邏輯組合，即可得到與全周期電感曲線成反比的全周期電流峰值包路線ipeak曲線。

2.2?全周期脈沖電流包絡線形成

全周期電流峰值包路線由脈沖電流峰值包路線和斬波電流峰值包路線兩部分組成，根據全周期脈沖電流包絡線提取過程，在脈沖注入和斬波控制兩個狀態切換過程中，會出現脈沖電流采集點較少，得到的包絡線精度不高。

1）當導通相開關管關斷時，相電流通過二極管開始續流，在此期間，如果注入脈沖，會產生負轉矩，并且延長相電流續流時間?所以要在相電流變為零時，開始注入脈沖，這樣就會形成續流I區域沒有采集到相電流峰值，圖3所示。

2）當導通相開關管開通時，相電流開始上升，上升的時間大小受電流斬波限i影響，并且此上升時間比固定斬波時間Δt大，所以，也會形成II區域沒有采集到相電流峰值，圖3所示。

對于以上兩種情況，I和II區域大小隨著開關角變化而變化，如果I和II區域大，得到的包絡線就不能很好的體現電感變化規律，最終會影響到位置估計精度。針對這種現象，為了提高該方法的通用性，采用擬合的方法，將I和II區域包絡線補全，這樣，就不受開通角和關斷角的影響，適合于變角度控制方式。

為了定量分析全周期脈沖電流包絡線的可行性，本文對[0，45°]一個電感周期脈沖電流峰值包路線和斬波電流峰值包路線進行實測，圖4為0～45°之間的全周期包絡線與轉子位置角關系曲線。

為了建立全周期包絡線與位置角之間的關系模型，采用曲線擬合的方法，考慮便于微處理器計算和算法的簡單，本文選擇多相式擬合方法求得θ-ipeak的數學模型為

θ=∑nm=0amimpeak。（6）

將圖4實測的數據，利用Matlab對式（6）進行多項式擬合，圖5為3階到7階式（6）多項式函數擬合的誤差曲線，由圖5可以看出，當階數是5時，擬合誤差平均最小，所以本文選擇階數n=5來擬合全周期電流包絡線與位置角之間的數學模型。

三相電感曲線呈周期性對稱，且兩兩相隔15°，由此可以得到12/8三相開關磁阻電機三相全周期包絡線與位置角之間的數學模型為

θA=∑5m=0amiA_peak，

θB=∑5m=0amiB_peak+15°，

θC=∑5m=0amiC_peak+30°。（7）

2.3?全周期包絡線位置估計

圖6為12/8結構開關磁阻電機全周期三相脈沖電流峰值包絡線與轉子位置關系圖，其中，iA-peak、iB-peak、iC-peak分別為A、B、C三相脈沖電流包絡線，與三相電感成反比，PA、PB、PC為三相轉子的位置信號，圖中橫坐標角度為A相位置角度，0°對應A相脈沖電流峰值的最大值，即A相電感最小處，由圖可以看出，三相脈沖電流包絡線交點分別對應轉子位置信號的邊沿，如圖中A相和C相脈沖電流包絡線的兩個交點P1、P2分別對應B相轉子位置信號PB的下降沿和上升沿時刻，所以只要比較A相和C相脈沖電流峰值即可估計出B相轉子位置信號的邊沿時刻，從而可以得到B相半周期導通的位置信號，同理，也可以比較其他兩相的脈沖電流包絡線得到A、C兩相的轉子位置信號的邊沿時刻以及半周期導通的位置信號。

根據圖6位置信號估計的原理，本文設計了一個簡易的邏輯比較電路來實現，如圖7所示，iA_peak、iB_peak、iC_peak三相脈沖電流峰值通過三個邏輯門電路比較得到PA、PB、PC三相轉子位置信號，例如當iC_peak大于iB_peak時，PA為1，即邏輯電路發出PA上升沿信號，iC_peak小于iB_peak時，PA為0，即邏輯電路發出PA下降沿信號，由于三相電流包絡線交接點在電感上升和下降過程中，電感變化率大，所以不同脈沖下的脈沖電流峰值變化大，從而提高了微處理器處理精度。

3?轉速估算

利用上述的全周期電流包絡線交截比較方法得到包絡線交點的位置檢索脈沖信號，如圖8所示。A相和B相的脈沖電流包絡線的交點為P1、P2、P3，其中P1和P3對應C相電感最大位置，P2對應C相電感最小位置，相鄰的兩個交點的位置檢索脈沖信號隔角為Δθ?=22.5°，因此記錄兩個相鄰的檢索脈沖信號上升沿時間間隔為Δt，即可通過式（8）、式（9）估算出電機轉速和C相位置信號。

n=ΔθΔt（deg/s）=60×Δθ360×Δt（r/min），（8）

θ（k+1）=θ（k）+ωΔt。（9）

其中：θ（k）為上次采樣時間估算的位置角;θ（k+1）為本次采樣時間估算的位置角;Δt為采樣時間。

4?仿真分析

為驗證理論的正確性，在Matlab/SIMULINK環境下搭建了三相12/8結構SRM全周期電流包絡線無位置傳感器仿真模型，主電路采用不對稱半橋，固定關斷時間Δt斬雙管方式，仿真參數：電機的額定功率為1.5?kW、額定轉速為1?500?r/min，Δt為1×10-5?s，注入的脈沖周期為0.000?1?s，占空比為10%。

4.1?全周期包絡線提取仿真

圖9為一相固定關斷時間斬波仿真模型，電流上限為10?A，固定關斷時間為1×10-5?s，下降沿觸發模塊完成時間相加，即當觸發模塊受到下降沿時輸出一個時間信號，該時間等于觸發時刻的時間加上一個延時時間，也就是固定關斷時間Δt，將系統運行時間與觸發模塊輸出的時間比較，當觸發模塊輸出的時間小于系統運行時間，比較器輸出信號將變為1，反之，比較器輸出信號為0，形成斬波控制PWM2，其他兩相的分析方法也一樣。

圖10為全周期電流峰值包絡線的提取過程仿真圖，從仿真波形可以看出，相電流仿真波形與圖2和圖3理論分析一致，非導通區域注入高頻脈沖，得到脈沖電流峰值電流波形，導通區域采用固定關斷時間斬波控制方式，導通區域相電流進行對稱數學處理后得到如圖10所示的斬波電流峰值電流波cc形，將脈沖電流峰值電流與斬波電流峰值電流進行異或邏輯處理即可得到全周期電流峰值包絡線。

4.2?位置估計仿真

圖11為電機運行在仿真條件為θon=0°，θoff=20°，斬波限i為2?A，轉速為400?r/min下的仿真結果，通過全周期電流峰值包絡線提取過程，得到三相全周期電流峰值包絡線，三相包絡線通過邏輯比較模塊，由B和C相包絡線比較估計A相轉子位置信號，從仿真結果圖可以看出，A相估計的轉子位置信號的邊沿時刻正好對應B和C相包絡線的交點，而且位置估計誤差也很小。

圖12為開通角θon=-2°，θoff=18°，斬波限i為2?A，轉速為600?r/min的位置估計仿真波形，從仿真圖看出，在變角度控制（APC）下，通過全周期電流峰值包絡線位置估計策略，仍能得到較高精度的A相估計位置信號。以上仿真結果驗證了所提的位置估計方法能在不同開關角下，都能得到全周電流包絡線，并能完成位置估計。

5?實驗驗證

為了驗證上述提出的位置估計策略的可行性，本文在一臺12/8結構SRM樣機上進行了實驗，圖13為系統結構圖，功率電路采用三相不對稱半橋結構。SRM樣機額定功率1.5?kW、額定額定轉速1?500?r/min。

硬件平臺如圖14所示，其中A為dSPACE主控系統、B信號調理電路、C為功率電路、D為SRM。控制器采用dSPACE1104+CPLD。

圖15為電機轉速420?r/min情況下的全周期電流包絡線提取實驗波形，其中，圖15（a）為非導通過程中脈沖電流峰值包絡線提取波形，通道1為脈沖電流波形，通道2是在PWM1下降沿采集的脈沖電流峰值，再通過擬合得到脈沖電流包絡線，圖15（b）是在開通角為0°和關斷角為20°下得到的全周期電流包絡線波形，通道1是脈沖注入和斬波控制兩個過程的相電流波形，通道2對應的全周期電流包絡線波形，此實驗結果與理論分析和仿真結果一致。

圖16（a）為開通角為-2°和關斷角為-18°下電機三相全周期脈沖電流包絡線的實驗波形，在PWM1的下降沿和PWM2的上升沿時刻采集電流值，通過擬合得到三相全周期包絡線，分別為iA_peak、iB_peak、iC_peak，然后將iA_peak、iB_peak、iC_peak通過比較邏輯運算電路估算出電機轉子的位置信號，圖16（b）為三相相電流波形和全周期包絡線比較得到的B相位置估計信號實驗波形，得到的三相脈沖電流峰值由式（7）估計出各相轉子位置角。由為了驗證該位置估計算法精度，實驗中將位置傳感器的位置信號與本文所提位置估計算法得到的位置信號進行比較，得到如圖17所示的位置估計誤差，從誤差比較可以看出，位置誤差都不超過0.3°之內，進一步驗證了該算法的正確性。

為了驗證本算法的優越性，與文獻[12]雙電流閥值的位置估計方法進行了實驗對比，圖18分別為轉速為100?r/min、350?r/min下雙電流閥值位置估計實驗波形圖，可以看出，轉速為100?r/min時，位置估計誤差Δθ達到0.67°，當轉速上升到350?r/min時，位置估計誤差Δθ達到1.6°，對比圖17本文所提算法的位置估計誤差，可以看出本文位置估計算法具有更高的位置估計精度。

6?結?論

針對脈沖電流注入方法需要預設電流閥值問題，本文在脈沖注入的理論基礎上，提出了一種全周期電流包絡線無位置傳感器技術，通過脈沖注入和斬波控制方式，分別提取電流包絡線，通過擬合等數學手段，得到與轉子位置關聯的全周期電流包絡線，該方法簡單、沒有增加硬件，可以實現多拍工作方式，通過仿真和實驗驗證了該方法的可行性和正確性。

參?考?文?獻：

[1]?FAHIMI?B，?EMADI?A，S?EPE?R?B?J.A?switched?reluctance?machinebased?starter/alternator?for?more?electric?car[J].IEEE?Transactions?on?Energy?Conversion，?2004，19（1）：116-124.

[2]?SADEGHI?S，?SADEGHI?R.?SADEGHI?M.Dynamic?performance?of?a?switched?reluctance?motor?for?propulsion?systems[C]//International?Symposium?on?Power?CElectronics，?Electrical?Drivers，?Automation?and?Motion.?Taormina?，?Italy：Nagasaki?University，2006：1419-1424.

[3]?Ravichandran?M?H，Sadasivan?Achari?V?T，Joseph?C?C，et?al.?Asimplified?design?methodology?for?switched?reluctance?motor?using?analytical?and?finite?element?method[C]//International?Conference?on?Power?Electronics?，Drives?and?Energy?Systems.New?Delhi，India：IEEE，2006：1-4.

[4]?SCHUZ?S?E，RAHMAN?K?M.?Highperformance?digital?PI?current?regulator?for?EV?switched?reluctance?motor?drives[J].IEEE?Transactions?on?Industry?Applications，2003，39（4）：1118-1126.

[5]?李景男，?王旭東，?周永琴.?基于兩相脈沖激勵的開關磁阻電動機無位置傳感器轉子位置檢測[J].?電機與控制學報，?2002，?6（1）：?6-9.

LI?Jingnan，?WANG?Xudong，?ZHOU?Yongqin.?Sensorless?rotor?position?detection?of?SRM?based?on?voltage?pulses?to?two?phase[J]?.Electric?Machines?and?Control，?2002，?6（1）：?6-9.

[6]?羅德榮，李亞雄，李孟秋.等.基于單閾值的開關磁阻電機無位置傳感器技術[J]?湖南大學學報（自然科學版）.2017.44（2）：94-100

LUO?Derong，?LI?Yaxiong，?LI?Mengqiu，?et?al.?Sensorless?technology?in?switched?reluctance?motor?based?on?the?single?threshold[J].?Journal?of?Hunan?University?（Natural?Sciences），2017，44（2）：94-100.

[7]?邵杰，?鄧智泉，?胡榮光.?基于改進脈沖注入開關磁阻電機無位置傳感器技術[J].電工技術學報，2015，30（21）：147-153

SHAO?Jie，?DENG?Zhiquan?，HU?Rongguang?.An?improved?sensorless?driving?method?of?switched?reluctance?motors?using?impressed?voltage?pulse[J].?Transactions?of?China?Electrotechnical?Society，?2015，30（21）：147-153.

[8]?李珍國，王紅斌，王江浩，等.基于電流波形檢測法的開關磁阻電動機無位置傳感器控制[J]?電工技術學報，2016，31（11）：97-104

LI?Zhenguo，?WANG?Hongbin，?WANG?Jianghao，?et?al.?Sensorless?control?of?switched?reluctance?motor?based?on?current?waveform?detection?method?[J].Transactions?of?China?Electrotechnical?Society，?2016，31（11）：97-104.

[9]?毛宇陽，?鄧智泉，?蔡駿，等.基于電流斜率差值法的開關磁阻電機無位置傳感器技術[J]?電工技術學報，?2011，21（9）：87-93.

MAO?Yuyang，?DENG?Zhiquan，?CAI?Jun，?et?al.?Sensorless?control?of?switched?reluctance?motor?based?on?current?slope?difference?method[J]?Transactions?of?China?Electrotechnical?Society?，?2011，21（9）：?87-93.

[10]?蔡駿，鄧智泉.?基于全周期電感法的開關磁阻電機無位置傳感器技術[J].電工技術學報，?2013，28（2）：145-153.

CAIJun，?DENG?Zhiquan.?Sensorless?control?of?switched?reluctance?motor?based?on?fullcycle?inductance?method[J].?Transation?of?China?Electrotechnical?Society，?2013，?28（2）：?145-153?.

[11]?周竟成，?王曉琳，?鄧智泉，?等，?鄒東坡.開關磁阻電機的電感分區式無位置傳感器技術[J].電工技術學報，?2012，27（7）：35-40.

ZHOU?Jingcheng，?WANG?Xiaolin，?DENG?Zhiquan，?et?al.The?position?sensorless?technology?of?switched?reluctance?motor?based?on?the?regional?comparison?of?threephase?inductance[J].?Transaction?of?China?Electrotechnical?Society，?2012，27（7）：35-40.

[12]?陳坤華，?孫玉坤，?李天博??開關磁阻電機無位置傳感控制器研究[J].電機與控制學報，2016，20?（3）：85-89.

CHEN?Kunhua，SUN?Yukun，LI?Tianbo.?Sensorless?control?of?switched?reluctance?motor[J].?Electric?Machines?and?Control，?2016，20（3）：85-89.

[13]?蒯松巖，李奎，衡鳳平，等.?考慮互感影響的開關磁阻電機無位置傳感器控制技術[J].電工技術學報，2017，32?（8）：178-186.

KUAISongyan，?LI?Kui?，?HENG?Fengping?，?et?al.Position?sensorless?technology?of?switched?reluctance?motor?considering?mutual?inductances[J].?Transaction?of?China?Electrotechnical?Society，?2017，32?32（8）：178-186.

[14]?蒯松巖，李興紅，馬金洋，等.??復平面電感模型開關磁阻電機中低速無位置傳感器技術[J].電機與控制學報，2015，19?（8）：1-8.

KUAI?Songyan，?LI?Xinghong，?MA?Jinang，et?al.Sensorless?control?of?switched?reluctance?motor?at?lowmedium?speed?based?on?complex?plane?modern?of?phase?inductance[J].?Electric?Machines?and?Control，?2015，19?（8）：1-8.

[15]?張磊，?劉闖，?王云林，等.開關磁阻電機變雙電流閥值的無位置傳感器技術[J].中國電機工程學報，2014，27?（34）：4683-4690.

ZHANG?Lei，?LIU?Chuang，?WANG?Yunlin，?et?al.?The?position?sensorless?technology?of?switched?reluctance?machines?based?on?double?variable?current?thresholds[J].?Proceedings?of?the?CSEE，2014.27（34）4683-4690.

（編輯：劉素菊）