面向控制的汽油直噴發動機軌壓系統建模

劉文憲 滕 勤 張 華

（1-合肥工業大學汽車與交通工程學院 安徽 合肥 230009 2-安徽公安職業學院信息網絡安全監察系）

引言

與進氣道燃油噴射（PFI）相比，汽油直噴（GDI）不存在進氣道濕壁效應，避免了進入氣缸的燃油滯后和冷起動過量供油，發動機不僅冷起動快及相應的排放降低，而且瞬態響應好、瞬態空燃比控制精度高。此外，較高的噴油壓力有利于燃油霧化，混合氣質量得以改善。研究表明，汽油噴霧油滴的蒸發冷卻作用，使充量系數和熱效率提高且爆燃傾向降低[1-2]。但是，這引入了一個附加的軌壓控制回路，使控制難度增大。而且，GDI發動機的軌壓系統是一個具有強擾動的復雜非線性動態系統，共軌壓力的波動將導致噴油器的噴油特性變化，使實際噴油量與期望噴油量出現偏差，燃燒室內的混合氣特性也隨之改變[3-4]。因此，軌壓控制的穩定性是燃油量精確控制的根本保障。

由于高壓油泵與發動機存在最佳的匹配關系，如果采用功率較大的高壓油泵，雖然低速時能夠產生較高的噴油壓力，但會造成高速時能耗過大，故而最大泵油量通常按照最大燃油需求量來設計。由于油泵轉速和泵油量隨發動機轉速而增大，且泵油效率也隨轉速而改變。因此，為了既保證起動時的軌壓快速建立和低速時的燃油霧化性能，又要使軌壓波動盡量小并在供油量需求最大時仍能足夠快地改變噴射壓力，且避免高速時過高的軌壓導致燃油系統高壓部件損壞和噴油量難于控制的問題，軌壓控制變得極為重要。

軌壓控制軟件設計通常采用基于模型的方法，其優勢在于：借助于閉環離線仿真，可以對策略與算法進行早期驗證，而且可以通過直接代碼生成，大大縮短軟件編程時間和開發周期，構建一個面向控制的GDI發動機軌壓系統模型則是其中的一個重要環節。

目前，面向控制的GDI發動機軌壓系統的建模大多用于控制器設計與仿真，最常見方法是用商用仿真分析軟件，如GT-SUITE、Modelica、AMESim等，選擇封裝好的模塊并進行連接，設定相關的參數后自動生成模型[5-7]。這類模型精度較高，但不便于生成微控制器的控制代碼。也可以基于流體動力學原理，通過一組微分方程和非線性靜態方程來建立物理模型[8]。為了簡化模型，可以根據軌壓的階躍響應特性，將系統描述成一階線性系統與擾動的組合，只考慮控制輸入與軌壓變化率的關系，而其它非線性影響因素均作為擾動，這需要設計主動抗擾控制器來抑制強烈的擾動[9]。當忽略系統的動態特性時，常常采用回歸分析方法，利用穩態實驗數據擬合一組多項式靜態模型來計算平均軌壓[10-11]。

本文按照GDI發動機高壓燃油系統物理結構和各部件的連接關系，基于燃油流量連續性方程和壓力微分方程建立軌壓系統動態數學模型，并利用MATLAB/SIMULINK搭建面向控制的軌壓預測模型。分別利用發動機轉矩和轉速突變時的軌壓階躍響應數據對模型進行檢驗，評判模型的精度、跟隨性和穩定性。

1 汽油直噴發動機軌壓系統

1.1 軌壓調節原理

GDI發動機燃油系統如圖1所示，由電動燃油泵、高壓油泵、高壓電磁閥、高低壓油管、共軌管和噴油器等組成。高壓油泵由發動機凸輪軸上油泵凸輪通過挺柱驅動，泵油量取決于凸輪升程，由一個電磁溢流閥調節。當電磁閥斷電時，燃油溢流回到低壓油路；當電磁閥通電時，溢流回路關閉。油泵內部柱塞的運動使燃油壓力升高，當油壓大于導軌內壓力時，燃油通過油泵出油口和高壓油管進入高壓燃油導軌。當導軌內部壓力大于設定的最大壓力時，燃油通過油泵內的限壓閥流回油泵。ECU通過控制電磁閥的閉合時間，改變壓油始點和壓油行程來調節高壓油泵輸出油量和壓力。

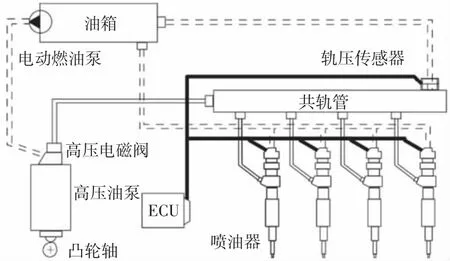
圖1 GDI發動機燃油系統

1.2 軌壓控制的基本結構

GDI發動機的軌壓控制結構如圖2所示，采用前饋+反饋的控制方式，控制輸出是對應于泵油持續角度的電磁閥閉合持續時間。目標軌壓由發動機轉速和轉矩需求確定，包括不同運行模式的map選擇、范圍與梯度限制，其中，需求轉矩由轉矩模型計算。前饋控制器用于提高控制的響應性，包括靜態補償和動態補償兩部分，前者的使能條件由發動機轉速、目標噴油量、目標軌壓、發動機啟動結束后的時間和燃油溫度來判定，控制增益根據目標軌壓、目標噴油量和發動機轉速確定；后者的使能條件是發動機啟動結束后的時間，根據發動機轉速與前后兩次目標軌壓變化量確定控制增益。反饋控制器采用PI算法，用來消除穩態偏差和擾動影響并防止超調，參數由軌壓偏差、發動機轉速和油溫確定。基于軌壓預測值軌壓處理模塊對測量軌壓進行校驗，防止軌壓誤判和消除振蕩。軌壓模型根據發動機轉速、目標噴油量、泵油持續時間來計算軌壓，其作用是：

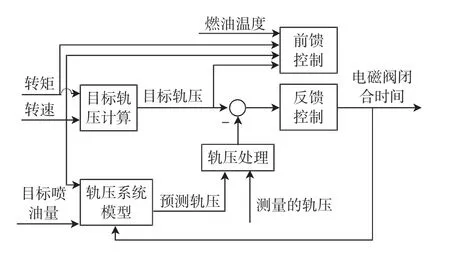
圖2 軌壓控制系統基本結構

1）提供閉環控制器所需的反饋信號或用其預測值對傳感器測量的軌壓進行校驗；

2）當軌壓傳感器出現故障時，可以利用模型估計值進行故障模式下的安全保護控制；

3）作為虛擬被控系統，用于軌壓控制策略和控制器的設計與仿真驗證。

2 軌壓系統數學建模

假設共軌系統各部分是剛性的，不發生形變。雖然燃油溫度會引起燃油密度變化，進而引起燃油壓力變化，但油溫變化是一個緩變過程，所帶來的是靜態誤差，對系統動態影響很小，且前饋控制器已經對油溫變化進行相應的補償，因此，建模過程中忽略了油溫對油壓的影響。根據質量守恒定律和流入、流出共軌系統的燃油相平衡的原則，得到圖3所示的燃油流動圖。

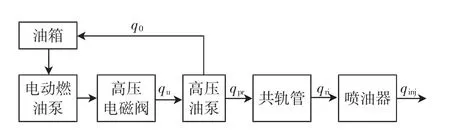
圖3 軌壓系統燃油流動圖

2.1 高壓油泵模型

高壓油泵壓油過程中，高壓腔容積和壓力隨著柱塞行程而變化，導致燃油密度變化，考慮燃油的可壓縮性，引入體積彈性模量。高壓油泵輸出油壓與泵腔內容積變化量、流入與流出高壓油泵的流量以及燃油泄漏量有關，其壓力方程如（1）式所示[12]。

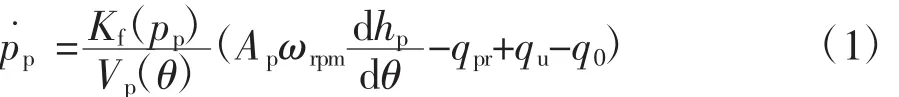
式中：Kf（pp）為高壓泵內燃油體積彈性模量，MPa；pp為柱塞腔內壓力，MPa；Vp（θ）為柱塞腔容積，m3；Ap為柱塞截面積，m2；hp為柱塞行程，m；ωrpm是凸輪軸轉速，rad/s；qu和qpr分別是流入和流出高壓油泵的燃油流量，m3/s；q0是燃油泄漏流量，m3/s。

流入高壓油泵的燃油流量由低壓燃油壓力和泵腔內的壓力決定，而油泵輸出的燃油流量由泵腔內壓力和共軌管內壓力確定，對應的流量方程如（2）、（3）式所示。

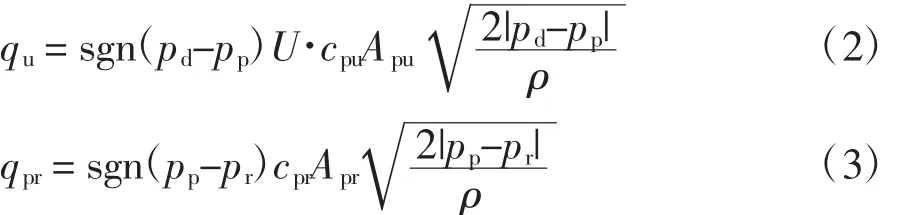
式中：sgn是符號函數，確定燃油流動方向；U是開關函數，電磁閥開啟時為1，關閉時為0；pd和pr分別是低壓燃油和共軌管內壓力，MPa；cpu和cpr分別是高壓油泵入口和出口處的流量系數，無量綱；Apu和Apr分別是高壓油泵入口和出口的有效截面積，m2。

2.2 共軌管模型

共軌管內壓力由流入和流出的燃油量決定，其變化率為[13]：

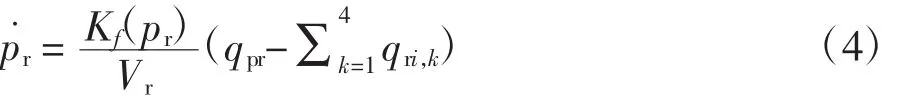
式中：Kf（pr）為共軌管內燃油體積彈性模量，MPa；qri，k為流入各個噴油器的燃油量（k代表噴油器編號），m3/s；Vr為共軌管容積，m3。

2.3 噴油器模型

噴油壓力可以根據流入噴油器的流量、噴油量得到，流入噴油器的燃油流量可以根據共軌管壓力和噴油器腔內壓力計算，噴油量則根據噴油器腔內壓力和缸內壓力計算，如（5）～（7）式所示[14]。

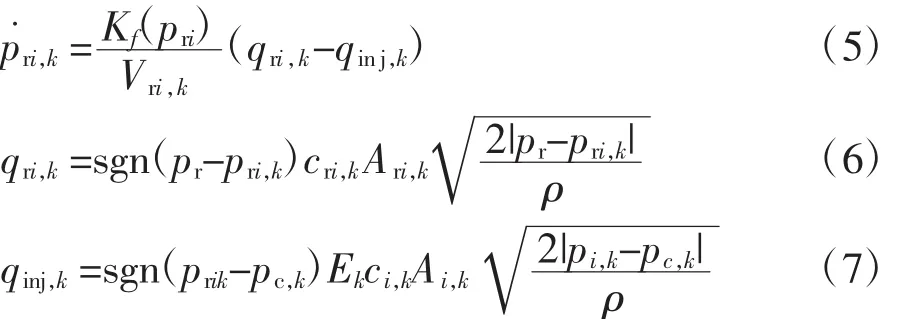
式中：Kf（pri）是噴油器內燃油體積彈性模量，MPa；Vri，k是噴油器腔內容積，m3；qinj，k是噴油流量，m3/s；pc，k是氣缸壓力，MPa；cri，k是噴油器入口流量系數，無量綱，Ari，k是噴油器有效進油面積，m2；ci，k是噴油嘴流量系數，無量綱，Ai，k是噴油嘴有效截面積，m2；Ek是噴油脈寬。

3 模型實現

為了簡化起見，忽略燃油泄漏量，根據（1）～（3）式建立的高壓油泵Simulink模型如圖4所示，模型輸入為發動機轉速、電磁閥開關信號、共軌管壓力，模型輸出為高壓油泵腔內壓力和出口流量。由于低壓燃油壓力較為穩定，對軌壓變化影響較小，故將其設為定值0.5 MPa。

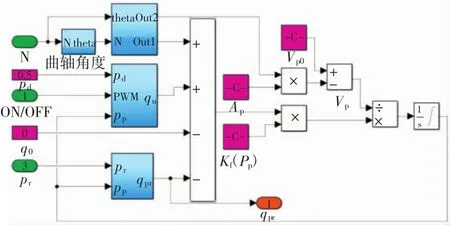
圖4 高壓油泵Simulink模型

根據（4）式建立的共軌管Simulink模型如圖5所示，輸入量為流入和流出共軌管的燃油流量，輸出量為共軌管壓力。

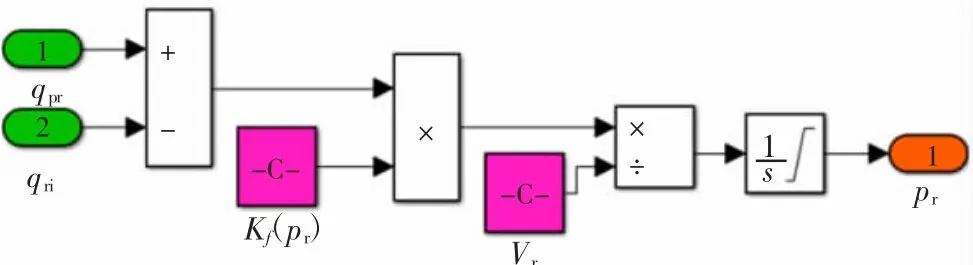
圖5 共軌管Simulink模型

根據（5）～（7）式建立的噴油器 Simulink 模型如圖6所示。模型的輸入為共軌壓力、氣缸壓力、轉速和目標循環噴油量。通過轉速確定循環時間，固定噴油正時，利用相應轉速下的目標循環噴油量確定噴油脈寬。輸出量為流入噴油器流量（提供給共軌管模型）和噴油器腔內壓力。其中，氣缸壓力由發動機轉速查取示功圖MAP確定。

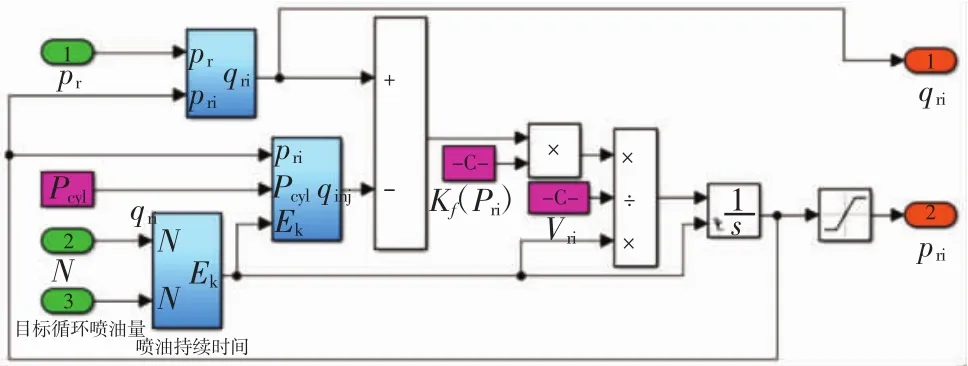
圖6 噴油器Simulink模型

將以上子模型封裝在一起，得到軌壓系統Simulink模型如圖7所示，輸入為發動機轉速、目標循環噴油量和泵油持續時間，輸出為估計的軌壓，模型的部分物理參數如表1所示。

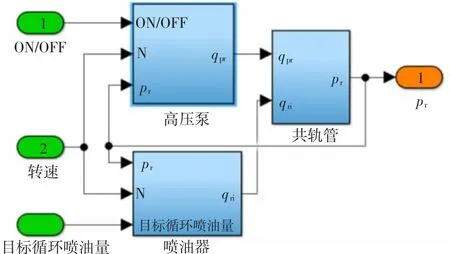
圖7 軌壓系統模型

表1 軌壓模型的部分參數mm

4 模型檢驗

4.1 試驗裝置與試驗方法

為了獲取驗證模型所需的數據，在配置有冷卻水恒溫系統（AVL 553）和燃油恒溫系統（AVL 753C）的AVL電力測功機（APA 202）試驗臺上，對一臺1.5L GDI發動機試驗，發動機主要參數如表2所示。分別使測功機工作在恒轉速和恒轉矩控制模式下，突變載荷和突變油門踏板位置，產生目標軌壓的階躍變化，通過總線接口模塊ETAS ES590和INCA軟件讀取ECU中的控制與測量參數。

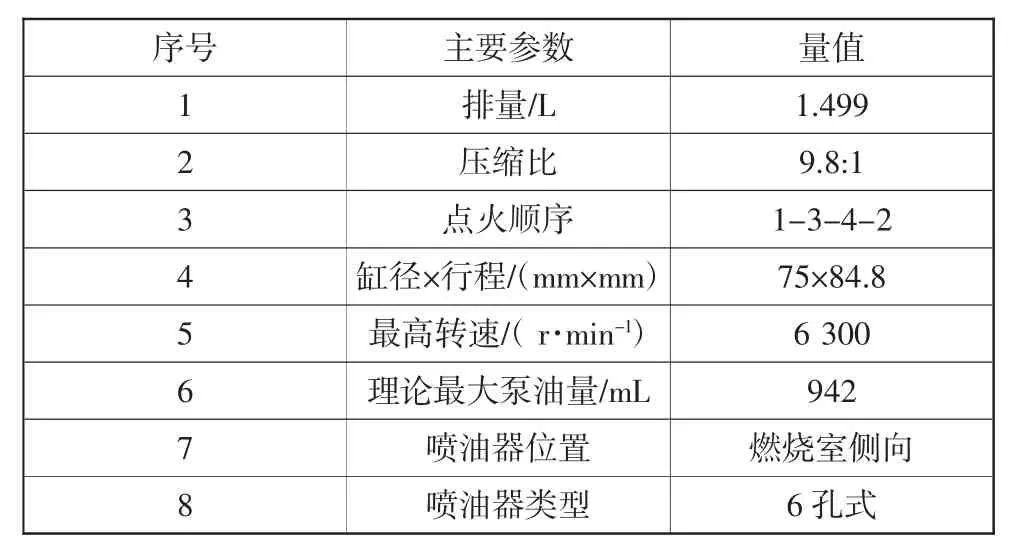
表2 試驗發動機主要參數

4.2 負載突變試驗

在發動機轉速為2 000 r/min和轉矩為11.8 N·m的穩定工況下，突然加大載荷，等待發動機穩定運行一段時間后，再突然減小載荷，發動機負載突變時的轉速和轉矩變化如圖8所示。

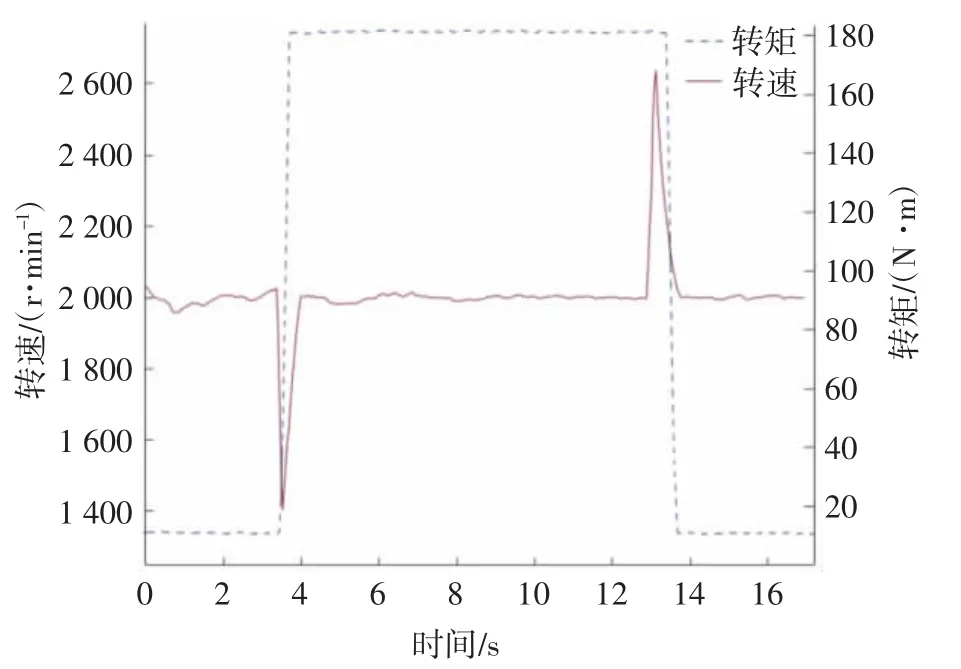
圖8 負載突變時的發動機轉速與轉矩曲線

載荷突變時，發動機轉速分別下沖到1 400 r/min和上沖到2 600 r/min，由于測功機控制系統快速調節油門，使ECU迅速將噴油量分別從5.2 mg/hub增加到39.8 mg/hub和從39.8 mg/hub減少到5.2 mg/hub以適應負載的變化，對應的發動機轉矩迅速分別從11.8 N·m增至180.2 N·m和從180.2 N·m減至11.6 N·m，使轉速恢復到初始狀態。噴油量突變使得軌壓從4.8 MPa到15.6 MPa和從15.6 MPa到4.9 MPa階躍變化，如圖9所示。

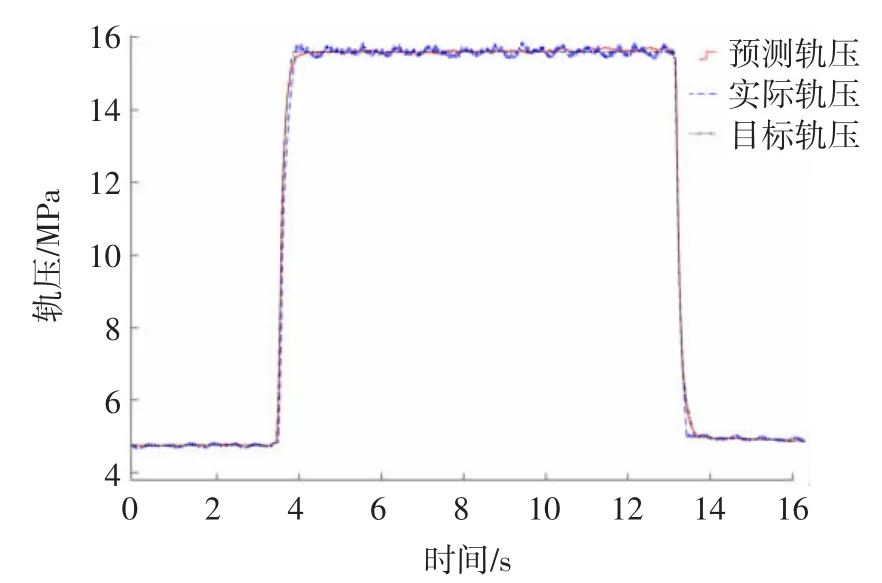
圖9 發動機負載突變時的軌壓階躍響應

4.3 轉速突變試驗

在發動機轉速為1 500 r/min和轉矩為72.3 N·m的穩定工況下，突然開大油門，發動機轉速快速提升到5 000 r/min；等發動機運行穩定后，再突然減小油門，發動機轉速快速回到初始轉速。對應的發動機的轉速和轉矩變化如圖10所示。

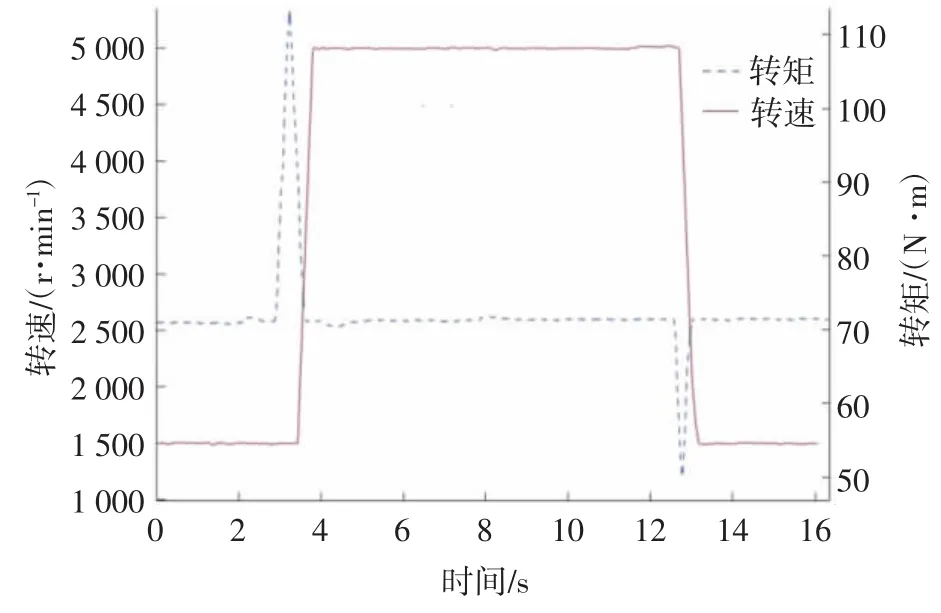
圖10 轉速突變時的發動機轉速與轉矩曲線

突然加速時，發動機轉矩出現112.9 N·m的上沖峰值，這種過沖現象是由駕駛員轉矩需求MAP中標定的調速特性和噴油量先升后降調節過程決定的，ECU先將噴油量從15.3 mg/hub快速增加到26 mg/hub，以保證發動機的加速性能；隨著油門踏板開度的穩定和轉速的上升，噴油量減少至18.5 mg/hub以防止飛車，使轉矩穩定在72.5 N·m。突然減速時，減速斷油使轉矩出現50.1 N·m的下沖峰值，由于達到復供轉速后恢復噴油，使轉矩回升到72.3 N·m，此時噴油量為15.2 mg/hub。油門位置的突變分別形成軌壓從7.6 MPa到12.8 MPa和從12.8 MPa到7.6 MPa的階躍變化，如圖11所示。

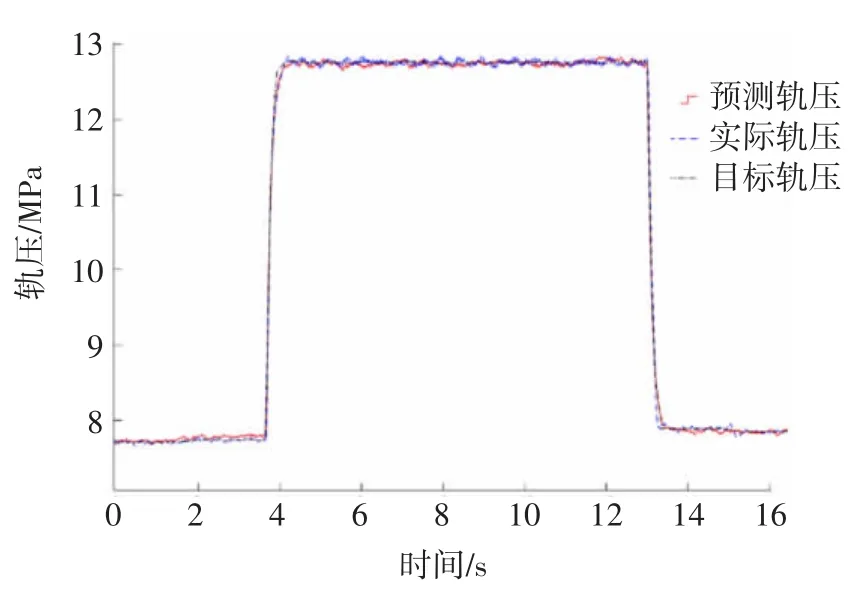
圖11 發動機轉速突變時的軌壓階躍響應

4.4 模型檢驗

4.4.1 模型精度按照（8）式計算模型擬合度R

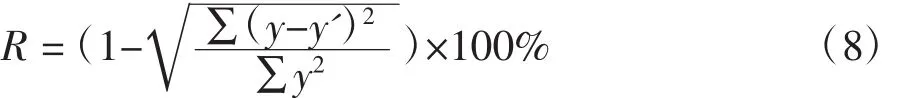
式中：y為測量的軌壓，y'為計算的軌壓。

負載突變時，軌壓正、負階躍響應的模型擬合度分別為98.46%和98.32%；轉速突變時，軌壓正、負階躍響應的模型擬合度分別為99.15%和98.93%，表明模型具有很高的精度。建模過程中，將低壓燃油壓力、噴射正時都設定為定值并忽略高壓油泵泄露量和油溫的影響，未對模型精度帶來顯著影響。

4.4.2 響應性

響應性體現了模型對實測數據的跟隨性能，利用上升時間來評價，定義為階躍響應曲線上從穩態值的5%到95%所經歷的時間。圖9中的軌壓正、負階躍變化時，模型估計值的上升時間分別是0.61 s和0.58s，實測軌壓的上升時間分別是0.57s和0.54s，均相差40 ms。圖11中的軌壓正、負階躍變化時，模型估計值的上升時間分別是0.47 s和0.48 s，實測軌壓的上升時間分別是0.46 s和0.45 s，分別相差10 ms和40 ms。

4.4.3 穩定性

模型的穩定性用從一個穩態進入另一個穩態后模型計算值與測量值的最大相對誤差來衡量，在圖9中負載突變時軌壓正、負階躍響應后的穩定階段，模型計算值與測量值的偏差小于±0.42MPa和±0.12MPa，對應的最大相對誤差分別為2.7%和2.5%。在圖11中轉速突變時軌壓正、負階躍響應后的穩定階段，模型計算值與測量值的偏差小于±0.31MPa和±0.17MPa，對應的最大相對誤差分別為2.3%和2.1%。

5 結論

針對GDI發動機高壓燃油系統，基于燃油流量連續性方程和壓力微分方程，建立了面向控制的軌壓系統模型，并利用發動機臺架上實測的軌壓階躍響應數據對模型進行了檢驗。

模型檢驗結果表明，無論是轉速突變還是負載突變，軌壓正、負階躍響應時的模型擬合度均高于98%，模型預測值與實測值的上升時間之差均小于40 ms，不同階躍響應穩態階段模型計算值與實測值的偏差和最大相對誤差分別小于±0.42 MPa和2.7%。表明模型具有良好的精度、動態跟蹤性能和準確性。

在基于模型的控制中，所建模型不僅可用于軌壓估計與預測、實時軌壓的校驗和診斷，而且可用于軌壓控制策略和控制器設計時的在環仿真與驗證。