基于AHP法的石河子發(fā)電廠周邊空氣質(zhì)量評(píng)價(jià)
張?zhí)煲悖瑢?川,王 健,苗世霞
(1.國(guó)網(wǎng)蘭州供電公司,甘肅 蘭州 730070;2.石河子大學(xué) 機(jī)械電氣工程學(xué)院,新疆 石河子 832003;3.石河子大學(xué) 兵團(tuán)空間信息工程技術(shù)研究中心,新疆 石河子 832003)
1 引言
近年來(lái)我國(guó)經(jīng)濟(jì)社會(huì)飛速發(fā)展,不斷加快的工業(yè)化、城市化進(jìn)程導(dǎo)致城市、農(nóng)村大氣環(huán)境污染問題日益突出[1]。以石河子為例,近些年秋冬季節(jié)大氣環(huán)境污染問題突出,尤其是以PM2.5為主要污染物造成的霧霾問題,影響面積大、波及范圍廣、持續(xù)時(shí)間長(zhǎng),對(duì)當(dāng)?shù)卮髿猸h(huán)境質(zhì)量造成了較為嚴(yán)重的后果。
環(huán)境評(píng)價(jià)可以揭示環(huán)境質(zhì)量狀況及其變化趨勢(shì),分析出污染治理的重點(diǎn)對(duì)象,為環(huán)境規(guī)劃和環(huán)境綜合治理方案提供依據(jù)[2]。空氣質(zhì)量評(píng)價(jià)體系具有單一指標(biāo)不相容性,是一個(gè)多項(xiàng)指標(biāo)共同參與決策的過程[3],因此,迫切需要建立一個(gè)科學(xué)、綜合且簡(jiǎn)便易行的綜合評(píng)價(jià)方法對(duì)環(huán)境質(zhì)量進(jìn)行描述。針對(duì)環(huán)境質(zhì)量等級(jí)評(píng)價(jià)方法,主要有層次分析法[4]、模糊綜合評(píng)價(jià)法[5]、灰色關(guān)聯(lián)分析法[6]、屬性識(shí)別分析法[7]、T. L. Saaty提出的層次分析法[8]等。
層次分析方法在環(huán)境質(zhì)量評(píng)價(jià)方面已經(jīng)得到了廣泛應(yīng)用,并取得了理想效果。本文以石河子市陽(yáng)光雙語(yǔ)學(xué)院與石河子南開發(fā)區(qū)農(nóng)田為實(shí)驗(yàn)區(qū)域,結(jié)合環(huán)境數(shù)據(jù)采集設(shè)備采集到二氧化碳、一氧化碳、PM2.5濃度數(shù)據(jù),選擇使用基于模糊原理的AHP法對(duì)實(shí)驗(yàn)區(qū)域進(jìn)行空氣質(zhì)量評(píng)價(jià)模型的構(gòu)建,并將實(shí)驗(yàn)結(jié)果與其他方法對(duì)比,取得了較為理想的結(jié)果,為今后在空氣質(zhì)量評(píng)價(jià)方法的應(yīng)用研究提供一定的借鑒意義。
2 數(shù)據(jù)處理方法
2.1 數(shù)據(jù)預(yù)處理方法
2.1.1 格拉布斯準(zhǔn)則
平臺(tái)在采集觀測(cè)數(shù)據(jù)時(shí)往往存在一些大誤差數(shù)據(jù),影響整個(gè)實(shí)驗(yàn)結(jié)果分析的正確性,為此,可以采用格拉布斯準(zhǔn)則[9]剔除此類數(shù)據(jù)。粗大誤差數(shù)據(jù)剔除后繼續(xù)利用準(zhǔn)則判斷,直至滿足準(zhǔn)則。樣本數(shù)據(jù)中是否存在大誤差數(shù)據(jù),可由下式完成判斷:
|Si|=|Xi-Xav|>G(n,Pa)·δ標(biāo)準(zhǔn)
(1)
在式(1)中,δ標(biāo)準(zhǔn):樣本數(shù)據(jù)標(biāo)準(zhǔn)差;G(n,Pa):格拉布斯常數(shù);Pa:置信度,文中取0.95。
2.1.2 相關(guān)系數(shù)
若有a、b兩組數(shù)據(jù),其平均值為分別為a1、b1。定義皮爾遜積矩相關(guān)系數(shù)[10]R為樣本數(shù)據(jù)協(xié)方差和標(biāo)準(zhǔn)差之間的比值,如下式(2):
(2)
R的值與1越接近,相關(guān)性越好,擬合結(jié)果越準(zhǔn)確。
2.2 AHP法理論
基于層次分析與模糊學(xué)相結(jié)合的AHP法[11]在空氣質(zhì)量模型構(gòu)建中效果較好,其具體算法流程如下:
2.2.1 因子集的選取
評(píng)價(jià)因子集的建立通過選擇二氧化碳、一氧化碳、PM2.5,如下式所示:
X={x1(CO2),x2(CO),x3(PM2.5)}
(3)
空氣質(zhì)量標(biāo)準(zhǔn)數(shù)據(jù)以官網(wǎng)為準(zhǔn)。
2.2.2 評(píng)價(jià)指標(biāo)集建立
按5個(gè)分級(jí)基準(zhǔn)將空氣質(zhì)量劃分為清潔、無(wú)污染、輕度污染、中度污染、重度污染,分別用y1、y2、y3、y4、y5表示,每個(gè)選定的評(píng)價(jià)因子yi對(duì)應(yīng)一個(gè)標(biāo)準(zhǔn)數(shù)據(jù),假定標(biāo)準(zhǔn)數(shù)據(jù)為si。構(gòu)建環(huán)境質(zhì)量評(píng)價(jià)級(jí)Y與si關(guān)系有:
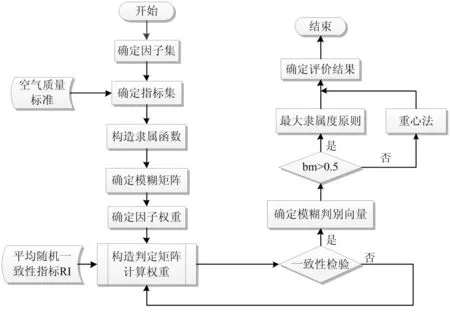
圖1 AHP算法流程
(4)
2.2.3 構(gòu)造隸屬函數(shù)
選擇隸屬函數(shù),確定隸屬關(guān)系uij(參考文獻(xiàn)[11])。
2.2.4 確定模糊矩陣
根據(jù)隸屬函數(shù),可得模糊矩陣如下式(5):
(5)
2.2.5 各因子權(quán)重計(jì)算
因子權(quán)重計(jì)算過程如下:
(1)判別矩陣Q建立。假定系數(shù)集A為:
A={A1,A2,A3,A4}
(6)
Ai表示第i中某因子觀測(cè)值比官網(wǎng)標(biāo)準(zhǔn)值,判別陣與A有以下關(guān)系式(7)。
(7)
(2)權(quán)重計(jì)算。計(jì)算A各行元素乘積:
(8)
計(jì)算Fi的n次方根:
(9)
歸一化向量:
(10)
計(jì)算矩陣最大特征根:
(11)
(3)檢驗(yàn)一致性。對(duì)A采用CR判斷其一致性,根據(jù)因子數(shù),RI取值為0.5258。
2.2.6 模糊向量計(jì)算
評(píng)判向量X與F之間有以下關(guān)系:
X=F°M
(12)
2.2.7 結(jié)果分析
模糊評(píng)價(jià)向量X={x1,x2,x3,x4,x5},取xm為x1,x2,x3,x4,x5中最大值,xm>0.5時(shí),xm即為對(duì)應(yīng)等級(jí);xm≤0.5時(shí),按下式計(jì)算。
(13)
3 實(shí)驗(yàn)方案與數(shù)據(jù)預(yù)處理
3.1 實(shí)驗(yàn)方案
采集實(shí)驗(yàn)總共選擇了兩個(gè)采集區(qū)域,分。第一個(gè)是石河子市陽(yáng)光雙語(yǔ)學(xué)校,第二個(gè)是石河子南開發(fā)區(qū)熱電廠。數(shù)據(jù)采集過程以30s為一個(gè)周期,采集十組數(shù)據(jù)取其平均值作為樣本數(shù)據(jù),并選取同時(shí)段的官網(wǎng)數(shù)據(jù)作為對(duì)照[12]。數(shù)據(jù)采集區(qū)域如下圖2a、圖2b所示。

圖2a 陽(yáng)光雙語(yǔ)學(xué)校

圖2b 南區(qū)熱電廠
3.2 實(shí)驗(yàn)數(shù)據(jù)預(yù)處理
3.2.1MG811電勢(shì)差與濃度函數(shù)關(guān)系
查閱文獻(xiàn)[12]可得,MG811型傳感器的靈敏度特性曲線可分為兩個(gè)區(qū)間,數(shù)據(jù)值如下表1所示。

表1 區(qū)間擬合參數(shù)
選取指數(shù)函數(shù)關(guān)系對(duì)上表數(shù)據(jù)進(jìn)行曲線擬合,結(jié)果如圖3。
由上圖結(jié)果可得:濃度與電勢(shì)差之間的函數(shù)關(guān)系滿足下式(14)、(15):
區(qū)間1:
(14)
區(qū)間2:
(15)
根據(jù)上式關(guān)系求得區(qū)間1、2上的決定系數(shù)分別為R1=0.996、R2=0.997,標(biāo)準(zhǔn)差分別為RMSE1=3.699、標(biāo)準(zhǔn)差RMSE2=0.771,滿足擬合條件,因此可根據(jù)式(14)、(15)函數(shù)關(guān)系將電勢(shì)差轉(zhuǎn)換為濃度值(注:二氧化碳標(biāo)準(zhǔn)數(shù)據(jù)單位為%,本文中單位為ppm,因此需要轉(zhuǎn)換單位)。轉(zhuǎn)換關(guān)系如下式(17):
|Si|=|Xi-Xav|>G(n,Pa)·δs
(16)
C=P/10000
(17)
3.2.2DSM501低脈沖率與粒子數(shù)函數(shù)關(guān)系
采集到的樣本數(shù)據(jù)不可避免會(huì)存在粗大誤差值,因此要對(duì)其進(jìn)行剔除。剔除粗差后得到的樣本數(shù)據(jù)如下表2。
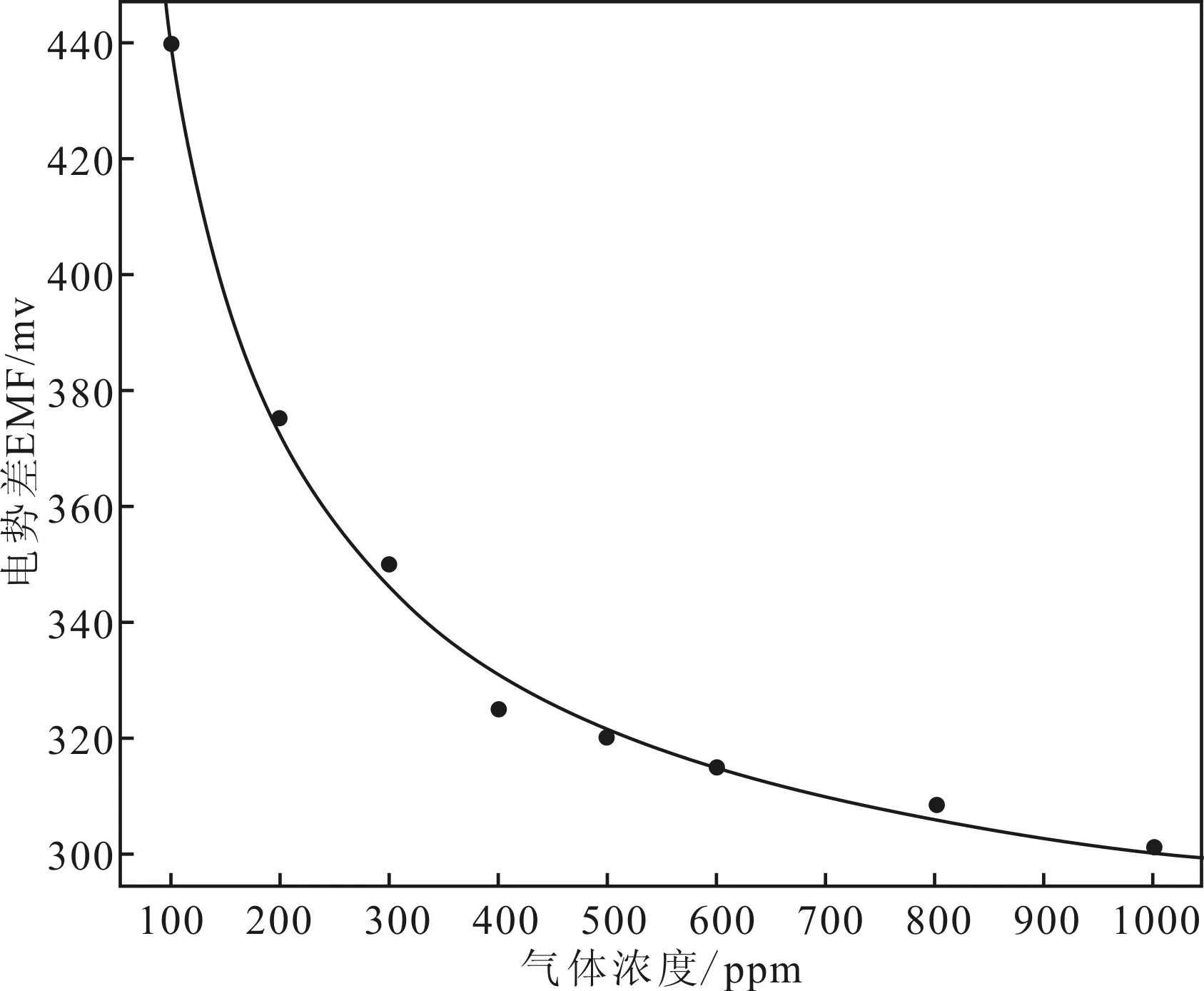
a 區(qū)間1擬合結(jié)果
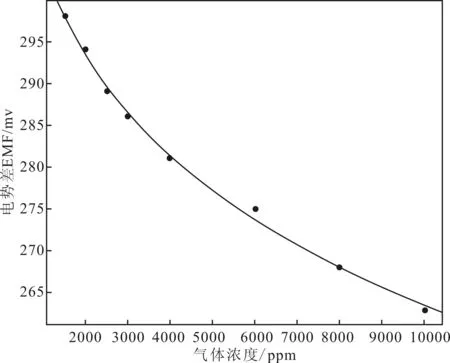
b 區(qū)間2擬合結(jié)果圖3 MG811電勢(shì)差與濃度關(guān)系
通過最小二乘法對(duì)上表數(shù)據(jù)中的低脈沖率和標(biāo)準(zhǔn)濃度值進(jìn)行擬合,得到如下圖4所示曲線。
由上圖可得,低脈沖率和標(biāo)準(zhǔn)濃度數(shù)據(jù)之間存在一元線性關(guān)系。為保證擬合關(guān)系的正確性,利用式(2)關(guān)系計(jì)算相關(guān)系數(shù)R,結(jié)果見下表3。
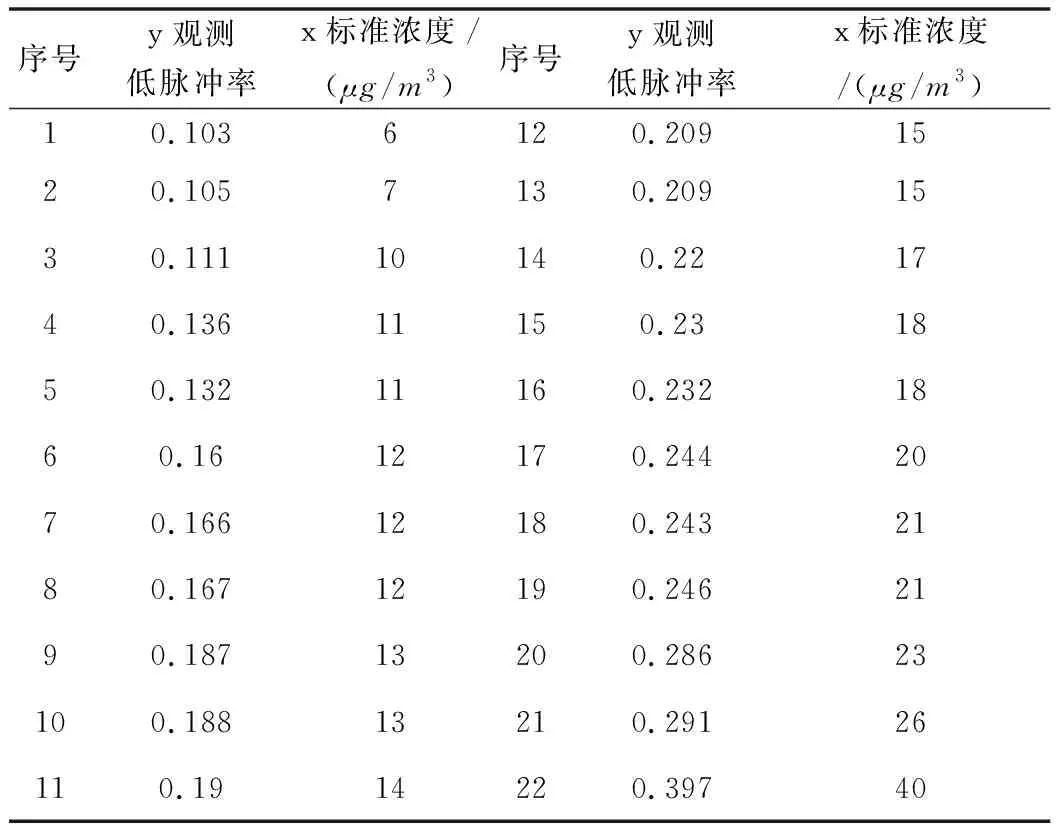
表2 樣本數(shù)據(jù)
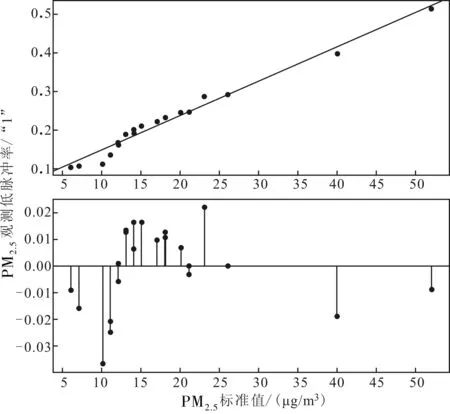
圖4 DSM501A低脈沖率和標(biāo)準(zhǔn)濃度值擬合表3 相關(guān)系數(shù)計(jì)算結(jié)果

對(duì)象SD觀測(cè)值(單位:“1”)SD標(biāo)準(zhǔn)值(單位:μg/m3)協(xié)方差(單位:μg/m3)RPM2.52.165239.096510.450.986
根據(jù)表(3)結(jié)果,相關(guān)系數(shù)R=0.986,比較接近1,說(shuō)明兩組數(shù)據(jù)相關(guān)性較好,且滿足一次線性函數(shù)關(guān)系,由此得如下式(18):
y=0.0089×x+0.059
(18)
3.2.3MQ-7電勢(shì)差與濃度函數(shù)關(guān)系
將MQ-7氣體傳感器采集的多組實(shí)驗(yàn)數(shù)據(jù)剔除粗大誤差,得到表4所示數(shù)據(jù)。
通過最小二乘法對(duì)上表數(shù)據(jù)中的電勢(shì)差和標(biāo)準(zhǔn)濃度擬合,得到如下圖5所示曲線。
根據(jù)圖5所示結(jié)果,得到函數(shù)關(guān)系如下式(19):
y=0.00008×x2-0.172×x+1.333
(19)
根據(jù)擬合結(jié)果得到方差0.129,決定系數(shù)0.976,標(biāo)準(zhǔn)差0.078,能準(zhǔn)確地反映測(cè)量值與官網(wǎng)標(biāo)準(zhǔn)值之間的函數(shù)關(guān)系。
4 AHP環(huán)境質(zhì)量等級(jí)評(píng)價(jià)模型評(píng)價(jià)
4.1 環(huán)境等級(jí)評(píng)價(jià)模型驗(yàn)證
空氣質(zhì)量等級(jí)評(píng)價(jià)模型的準(zhǔn)確性需要進(jìn)行驗(yàn)證。本文隨機(jī)選取了樣本組數(shù)據(jù)中的3號(hào)樣本數(shù)據(jù)最模型可靠性進(jìn)行驗(yàn)證,驗(yàn)證結(jié)果如下表所示。
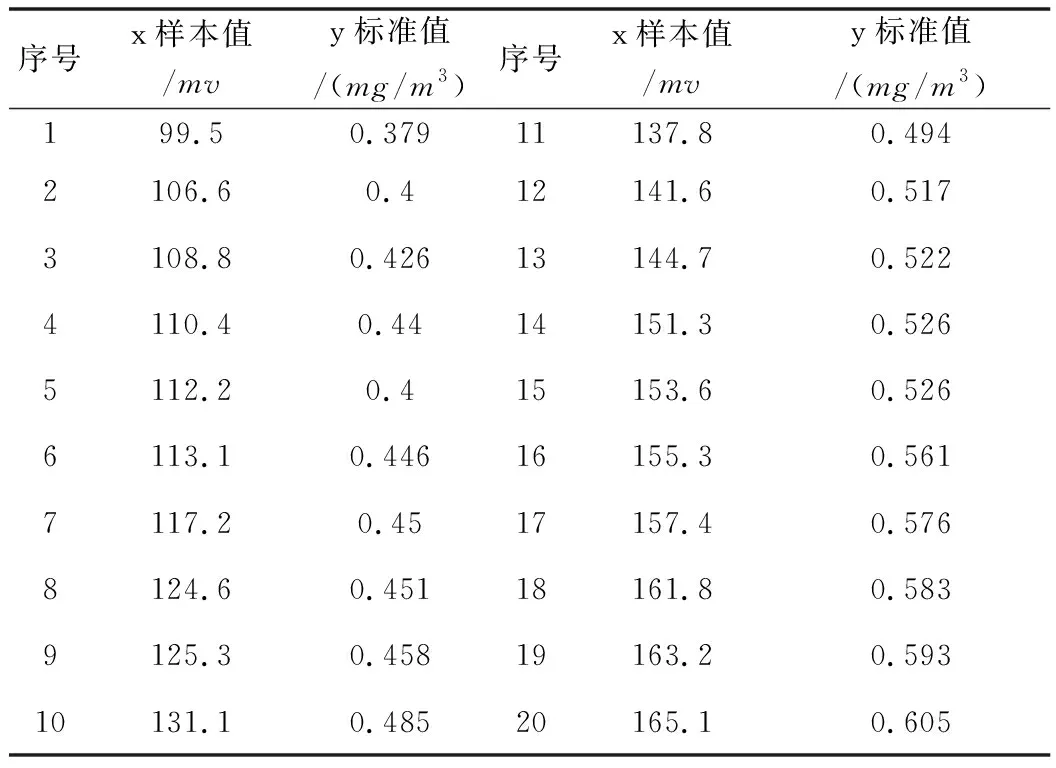
表4 樣本數(shù)據(jù)與官網(wǎng)數(shù)據(jù)對(duì)照

表5 示例數(shù)據(jù)
根據(jù)公式(6)—(11)計(jì)算可得:評(píng)價(jià)向量X=[0.340.66 0 0 0]T,權(quán)重E=[0.52 0.12 0.36]T。參考最大隸屬度原則,取xm=0.66,則空氣質(zhì)量等級(jí)為無(wú)污染,結(jié)果可靠。
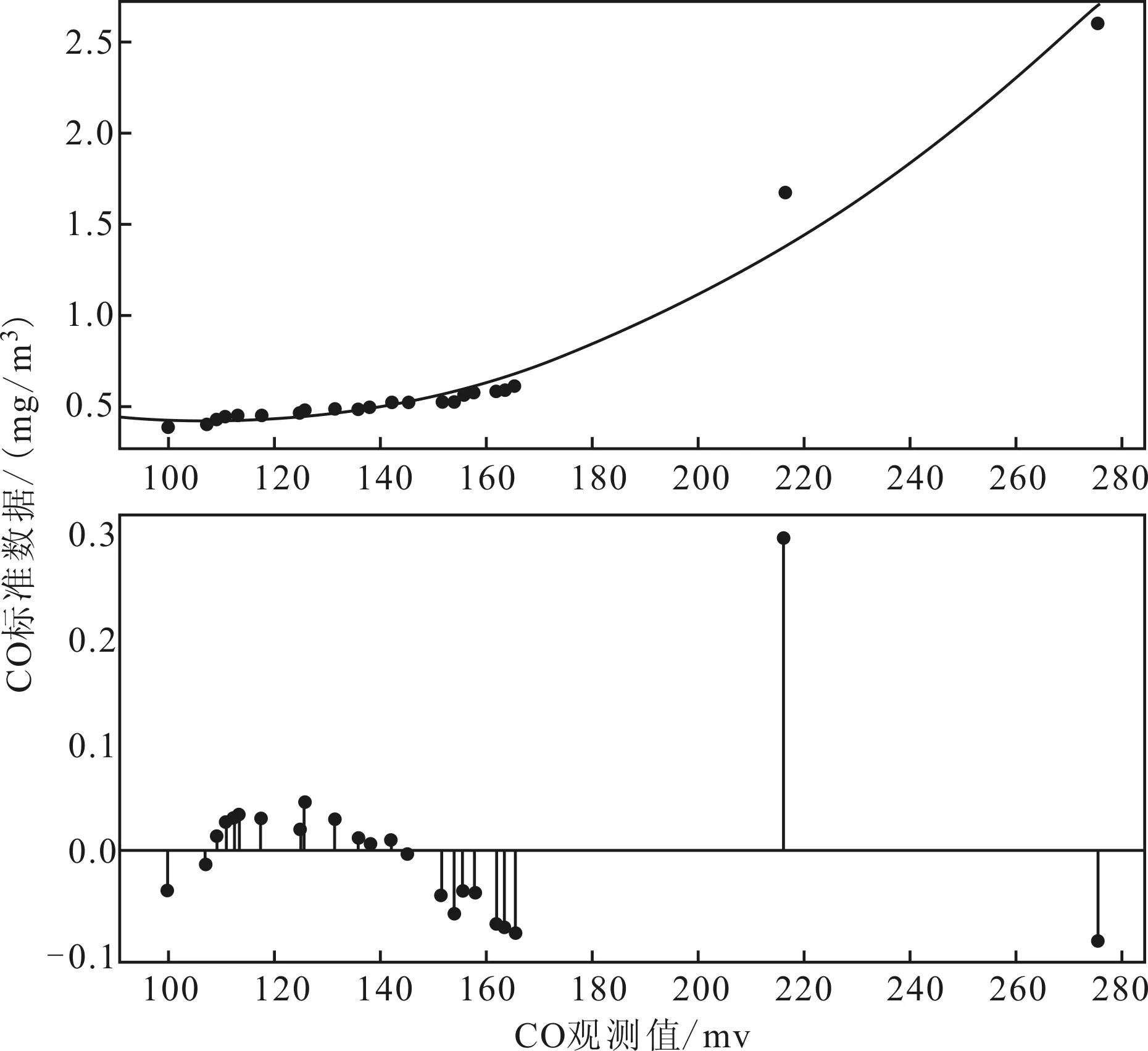
圖5 MQ-7電勢(shì)差和標(biāo)準(zhǔn)濃度值擬合曲線
4.2 AHP評(píng)價(jià)模型驗(yàn)證結(jié)果分析
繪制實(shí)驗(yàn)采集的30組數(shù)據(jù)評(píng)價(jià)結(jié)果統(tǒng)計(jì)圖,如下所示。

圖6 樣本數(shù)據(jù)評(píng)價(jià)結(jié)果統(tǒng)計(jì)
針對(duì)采集的30組實(shí)驗(yàn)數(shù)據(jù),分別將用AHP評(píng)價(jià)法建立的環(huán)境等級(jí)評(píng)價(jià)結(jié)果和官網(wǎng)公布的空氣污染等級(jí)進(jìn)行對(duì)比驗(yàn)證。根據(jù)單因子設(shè)制原則,本文將清潔、無(wú)污染等級(jí)視為合格,用“0”表示;輕度污染、中度污染、重度污染視為不合格,用“1”表示[12]。根據(jù)上圖分析,在30組樣本數(shù)據(jù)中,有28組數(shù)據(jù)的結(jié)果與官網(wǎng)公布空氣質(zhì)量等級(jí)一致,只有“11”、“23”號(hào)不一致,準(zhǔn)確率達(dá)到93.33%,由此證明了該方法可用性和準(zhǔn)確性。
5 結(jié)語(yǔ)
本文針對(duì)采集到的石河子市及發(fā)電廠周邊二氧化碳濃度、一氧化碳濃度、PM2.5濃度值數(shù)據(jù),采用了AHP法建立了空氣質(zhì)量評(píng)級(jí)模型,對(duì)試驗(yàn)區(qū)域的空氣質(zhì)量等級(jí)進(jìn)行了評(píng)價(jià),并與單因子分析法對(duì)比驗(yàn)證其可靠性,效果較為理想,具有一定參考意義。但針對(duì)本文的研究方案在環(huán)境等級(jí)評(píng)價(jià)方面仍具有局限性:①實(shí)驗(yàn)過程只采集了二氧化碳、一氧化碳、PM2.5這三種污染物作為評(píng)價(jià)因子,評(píng)價(jià)因子種類較少,不具備多樣性;②實(shí)驗(yàn)驗(yàn)證只是與單因子評(píng)價(jià)法進(jìn)行了對(duì)比,并沒有與AQI指數(shù)實(shí)現(xiàn)對(duì)比驗(yàn)證;③鑒于AHP法在評(píng)價(jià)過程中確立的指標(biāo)體系需要有專家系統(tǒng)支持,給出的指標(biāo)是否合理決定了評(píng)價(jià)模型的準(zhǔn)確性。
針對(duì)以上不足,今后仍需在評(píng)價(jià)因子選取多樣性、多重評(píng)價(jià)模型驗(yàn)證對(duì)比、AHP法指標(biāo)體系的優(yōu)化算法設(shè)計(jì)等方向繼續(xù)研究。

