基于改進二進制粒子群算法的配電網多目標重構

， ，

(國網四川省電力公司技能培訓中心，四川 成都 611133)

0 引 言

配電網作為電力系統中直接與需求側連接的關鍵部分，其作用是向用戶提供安全、經濟及可靠的電能供應，因此，配電網的安全高效運行至關重要。在滿足各種約束條件的情況下，配電網重構能夠尋找到實現配電網安全高效運行的最優拓撲結構，是配電自動化技術研究的主要內容之一，也是智能電網的重要功能之一[1-2]。

現階段已有不少對配電網重構的研究，從目標函數的構造上來說，既有單目標重構，也有多目標重構；從優化算法上來說，目前各種人工智能算法在配電網重構中得到了廣泛的應用。各種不同的重構優化方法各有側重，也各有優缺點。文獻[3]以系統有功網損、線路功率傳輸裕度以及節點電壓偏移構建重構優化的多目標函數，通過隸屬度函數和歐式距離算法將多目標優化問題轉化為單目標問題，采用改進的二進制粒子群算法迭代尋優。文獻[4]研究了利用改進和聲搜索算法對含有分布式發電(distributed generation,DG)的配電網多目標重構問題，但只是將DG作為“負”的負荷進行潮流計算，DG模型較簡單。文獻[5]提出一種離散學習優化算法，對含有DG的配電網進行以有功網損最小為目標的單目標重構研究，算法較復雜不易實現。文獻[6]提出了一種基于無重訪機制的NSGA-Ⅱ算法，用于求解使配電網有功網損降低和供電可靠性提高的多目標重構問題，該算法能夠有效避免重復計算，提高求解效率。

這里提出以網絡有功網損和網絡電壓偏移兩個指標來構建多目標配電網重構的目標函數，借助網絡初始狀態將量綱不同的指標進行歸一化處理。考慮對網絡重構效果的側重性，利用權重系數法將多目標函數轉化為單目標函數，調度人員可根據需要調整各指標的權重系數。運用改進二進制粒子群算法求解所建立的多目標配電網重構數學模型，得到滿足各種約束條件的配電網安全經濟運行的最優拓撲結構。

1 數學模型

1.1 多目標函數

網絡有功網損的高低能夠反應配電網經濟運行狀況的優劣，網絡電壓偏移是反應配電網電能質量的一項重要技術指標，下面利用以上兩個指標構建多目標函數。

1) 網絡有功網損

(1)

式中：Ploss為網絡的有功網損；n為網絡中的總支路數；ki為開關i的狀態，k=1為開關閉合，k=0為開關斷開；Ii為流過支路i的電流；Ri為支路i的電阻。

2) 網絡電壓偏移

(2)

式中：Ubias為網絡的電壓偏移；m為網絡中的節點總數；Ul為節點l處的實際電壓；UlN為節點l處的額定電壓，一般取UlN=1。

3) 構建多目標函數

首先，利用配電網初始拓撲結構所對應的系統指標將上述兩個指標進行歸一化處理，以解決數量級、量綱等不同的問題。再通過加權求和的方式將多目標函數轉化為單一目標函數，可表示為

(3)

式中：F為目標函數；Ploss0為配電網初始狀態下的有功網損；Ubias0為配電網初始狀態下的電壓偏移；ω1、ω2分別為網絡有功網損和網絡電壓偏移的權重系數，滿足ω1+ω2=1。

1.2 約束條件

1) 網絡潮流約束

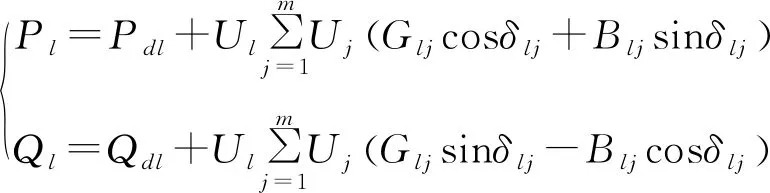
(4)

式中：Pl、Ql分別為節點l處注入的有功功率和無功功率；Pdl、Qdl分別為節點l處負荷的有功功率和無功功率；Glj、Blj、δlj分別為節點l、j之間的電導、電納和相角差；m為網絡中的節點總數；Ul、Uj分別為節點l、j處的電壓幅值。

2) 支路功率約束

Si≤Simax

(5)

式中：Si為支路i中流過的功率；Simax為支路i中允許流過的最大功率。

3) 節點電壓約束

Ulmin≤Ul≤Ulmax

(6)

式中，Ul、Ulmax、Ulmin分別為節點l處的實際電壓及其上、下限。

4) 網絡拓撲約束

重構過程中配電網的拓撲結構必須是連通的且呈輻射狀，不存在環路及孤島。

2 重構算法設計

2.1 改進的二進制粒子群算法

標準的粒子群算法(particle swarm optimization,PSO)是由Kennedy等人受到鳥類在搜尋食物的過程中，出現的遷徙和群集行為的啟發而提出的[7-8]。后來，他們為了解決離散空間域的優化問題，于1977年提出了二進制粒子群算法(binary particle swarm optimization,BPSO)。

在BPSO中，每個粒子根據式(7)更新自己速度：

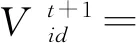
(7)

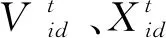
粒子位置更新公式為

(8)

式中：r為0至1之間服從均勻分布的隨機數；Sx為Sigmoid函數：

(9)

由于配電網重構屬于一種規模較大的混合整數非線性規劃問題，BPSO在解空間搜索過程中非常容易陷入局部最優域而無法跳出，導致搜索結果收斂于局部最優而不是全局最優。為了克服此不足，利用改進的二進制粒子群算法[9]對所建的配電網重構數學模型進行求解。為合理平衡BPSO全局和局部搜索能力，對式(7)中的慣性權重系數ω進行改進，改進之后的慣性權重系數不再是一常數，而是能夠隨著搜索的進行不斷地非線性遞減，這樣有助于算法跳出局部最優。改進慣性權重系數公式為

(10)

式中：ωmax、ωmin分別為慣性權重系數的最大、最小取值，其取值范圍通常為0.4～0.95；t、tmax分別為當前迭代次數和最大迭代次數。

改進之后，在迭代初期，ω較大，算法具有較強的全局搜索能力，能夠讓粒子盡可能快地搜索整個解空間，找到全局最優解所在的鄰域。當迭代進行到中期，ω逐漸地非線性減小，粒子搜索范圍也以全局最優解鄰域為中心逐漸縮小。到了迭代后期，基于指數函數非線性變化的特點，ω會加速減小，算法的局部搜索能力得到增強，粒子就能夠在全局最優解鄰域搜索到全局最優解。引入非線性調整慣性權重系數的BPSO的全局搜索效率和收斂速度均得到提高，稱為非線性調整慣性權重二進制粒子群算法(ULWBPSO)，流程如圖1所示。

2.2 其他說明

1) 編碼原則

通常，配電網都是閉環設計而開環運行的，可以說一個聯絡開關決定一條環路，因此采用了基于環路的編碼原則。

在使用的ULWBPSO中，每個粒子的維度即為配電網中聯絡開關的個數，每一維的數字即為需要斷開的開關編號；與電源直接相連的開關和不在任何環路上的開關由于必須閉合不參與編碼；為保證配電網呈輻射狀運行，每個環路只能斷開一個開關，且每個環路斷開的開關編號必須互不相同且不在同一支路上[10]。

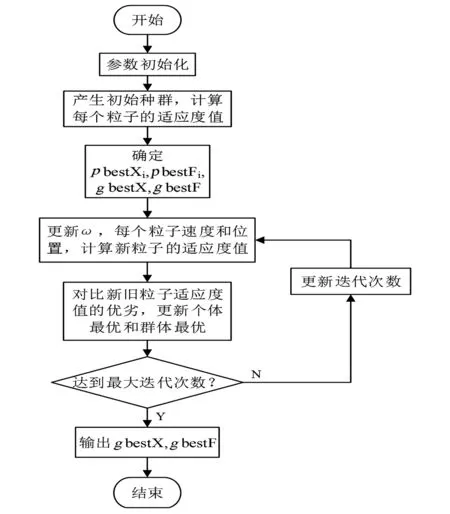
圖1 ULWBPSO流程

2) 無效解的處理

基于環路的編碼原則產生的粒子并不全是有效解。部分粒子所對應的配電網拓撲結構可能呈輻射狀，但是卻不滿足連通性的要求，會出現孤島存在的情況。因此需要對初始粒子和迭代更新后的粒子進行有效性檢驗：首先，每個粒子所對應的配電網拓撲結構必須呈輻射狀；然后根據圖論并結合樹狀結構特點，對每個粒子所對應的配電網拓撲結構連通性進行判斷[11]。這樣的處理可以避免無效解的產生，提高算法搜索效率。

3 算例分析

所用的重構算例來自文獻[12]，為IEEE 33節點配電網系統，系統額定電壓為12.66 kV，共有33個節點和37條支路，含有5個聯絡開關，編號分別為(33,34,35,36,37)，系統總負荷為(3715+j2300)kVA，單線圖如圖2所示。ULWBPSO的參數設置為：粒子群規模sizepop=40，最大迭代次數tmax=50，慣性權重系數ωmax=0.95、ωmin=0.4,加速系數c1=c2=1.496 2。指標權重系數ω1=ω2=0.5(有功網損和電壓偏移指標同等重要)。以式(3)為目標函數，采用ULWBPSO尋優，仿真結果如表1所示。

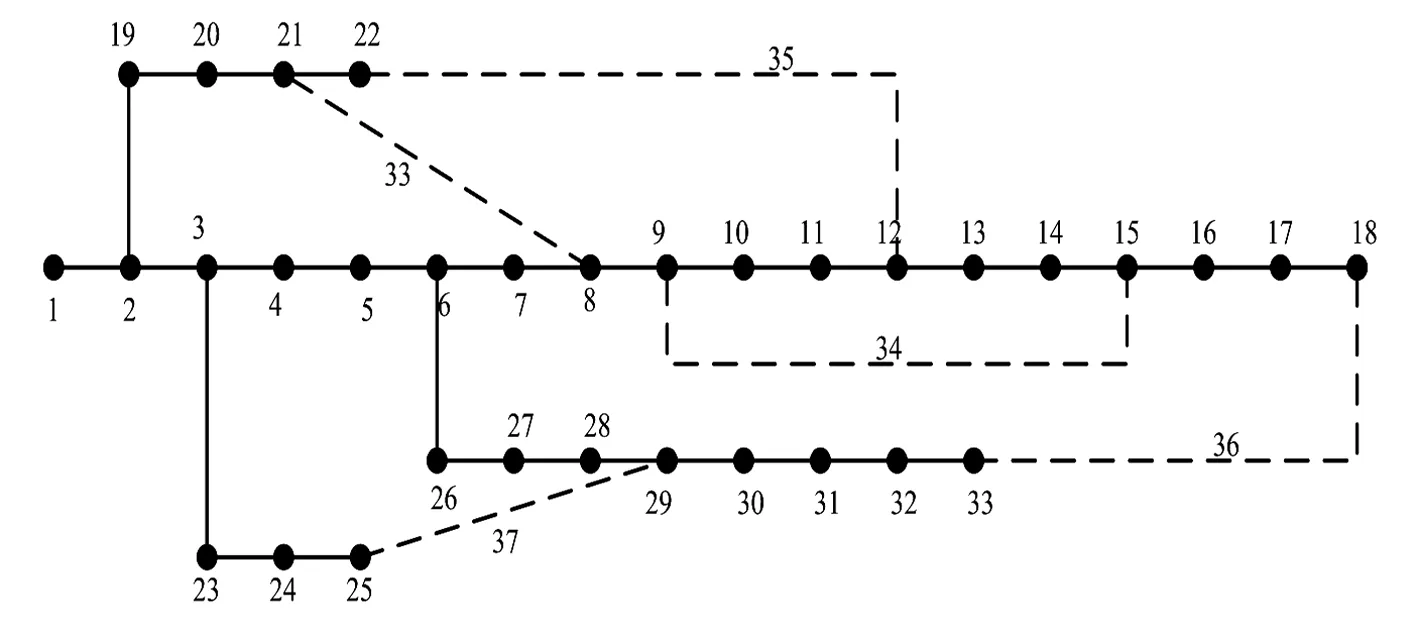
圖2 IEEE 33節點系統

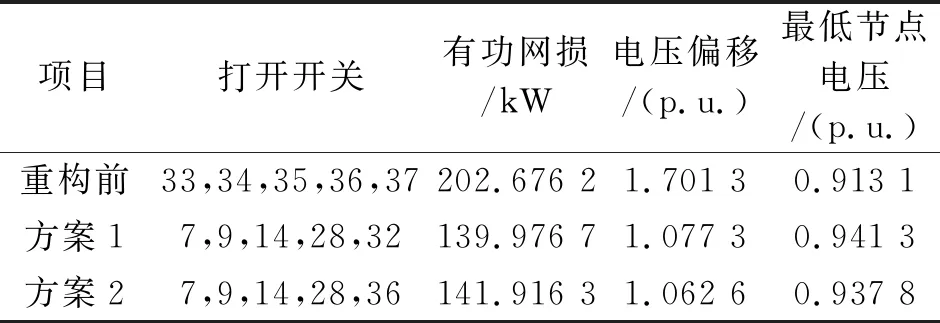
項目打開開關有功網損/kW電壓偏移/(p.u.)最低節點電壓/(p.u.)重構前33,34,35,36,37202.676 21.701 30.913 1方案17,9,14,28,32139.976 71.077 30.941 3方案27,9,14,28,36141.916 31.062 60.937 8

由表1可知，網絡重構之后，系統的有功網損和電壓偏移均得到了有效降低，且最低節點電壓也得到了明顯提高。

方案1將有功網損降低到139.976 7 kW，降低率為30.94%，將電壓偏移降低到1.077 3 p.u.，降低率為36.68%，將最低節點電壓提高到0.941 3 p.u.，提高率為3.09%。

方案2將有功網損降低到141.916 3 kW，降低率為29.98%，將電壓偏移降低到1.062 6 p.u.，降低率為37.54%，將最低節點電壓提高到0.937 8 p.u.，提高率為2.71%。

方案1對有功網損的改善略優于方案2，而方案2對電壓偏移的改善略優于方案1，但差距不明顯，綜合考慮兩個方案的最低節點電壓，認為方案1為最佳重構方案。重構前、方案1、方案2的系統節點電壓如圖3所示。

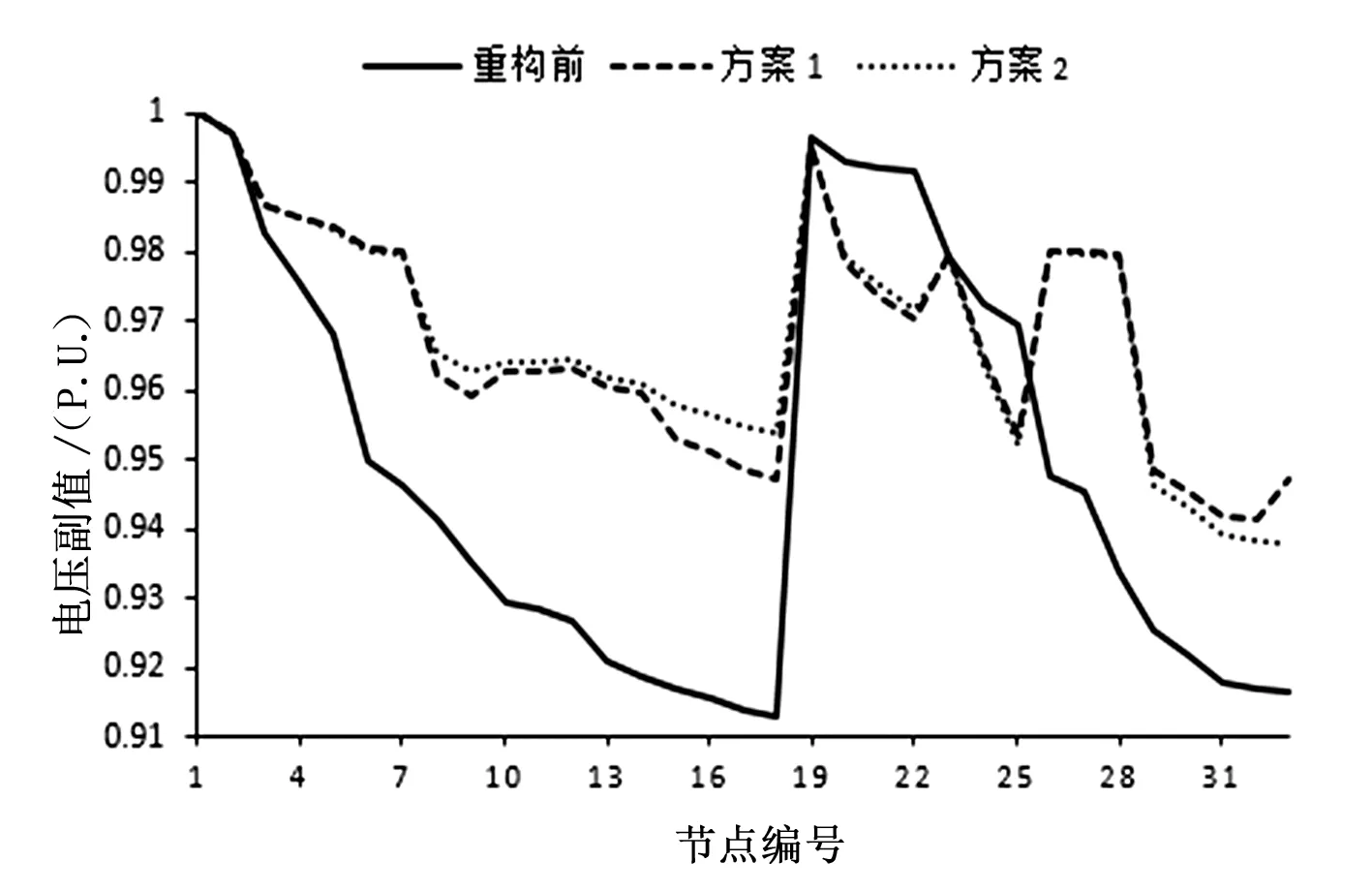
圖3 節點電壓水平

為了驗證改進二進制粒子群算法(ULWBPSO)的性能，分別使用ULWBPSO與BPSO對IEEE 33節點系統進行重構仿真。分別記錄兩種算法獲得50次全局最優解的迭代次數，如圖4所示。

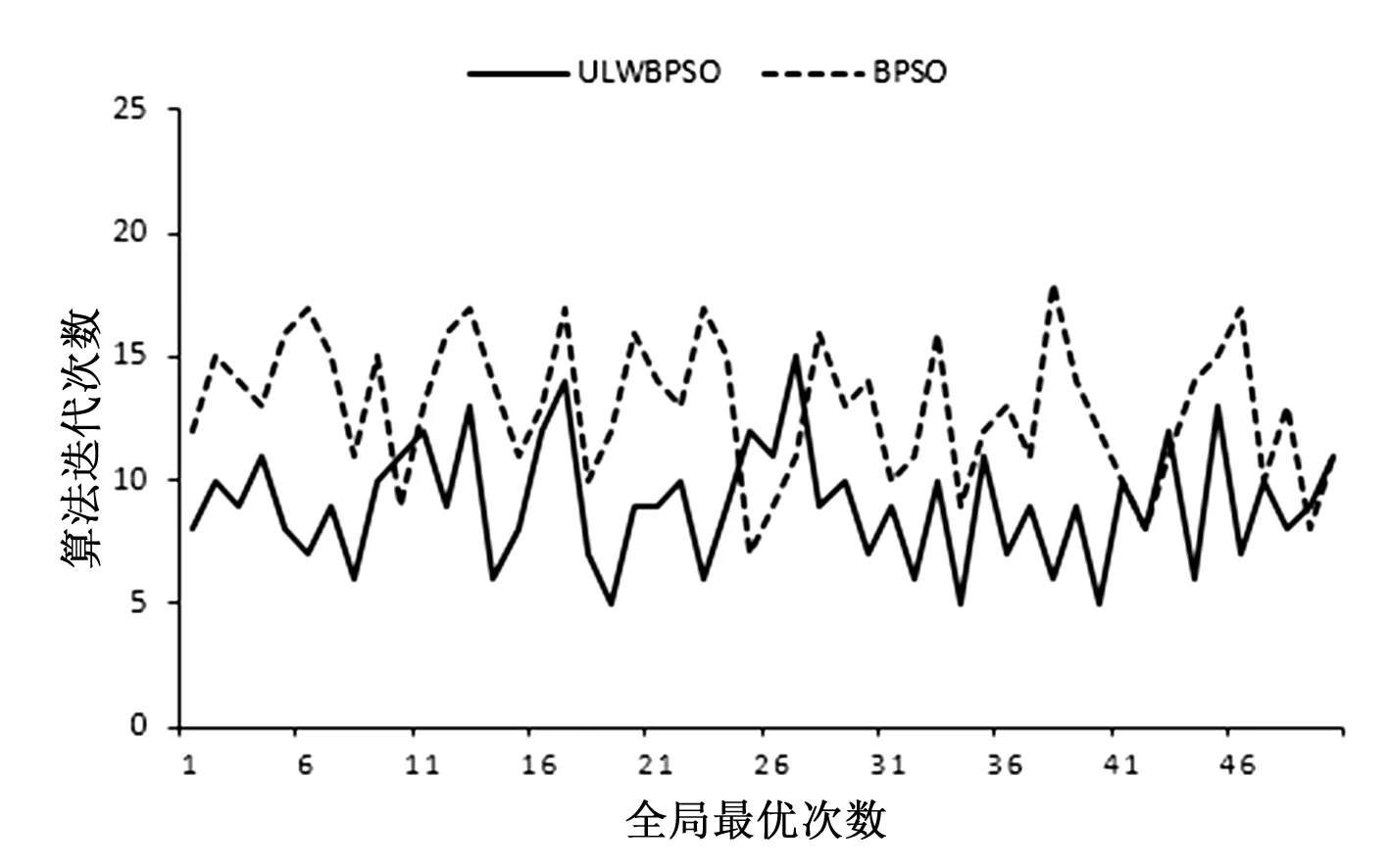
圖4 迭代次數對比

從圖4中可以看出，ULWBPSO獲得全局最優解所需的迭代次數明顯低于BPSO。ULWBPSO、BPSO獲得全局最優解的平均迭代次數分別為9.06次、12.96次，表明通過引入非線性動態調整的慣性權重系數，算法的全局搜索效率和收斂速度得到一定提高。將所提算法與其他文獻算法進行比較，結果如表2所示，表明所得算法具有一定優勢。

表2 算法比較

4 結 語

提出以配電網有功網損和網絡電壓偏移構成多目標函數，并根據網絡初始狀態對多目標歸一化處理并加權求和，將其轉化為單目標函數。將非線性動態調整的慣性權重系數引入二進制粒子群算法，提高其全局搜索效率和收斂速度。仿真結果表明，所提出的方法能夠對配電網進行有效重構，降低系統有功網損和電壓偏移，提高配電網運行的經濟性和可靠性，易于實際應用來提高配電網自動化水平。