車聯網環境下公交路徑交通狀態估計方法研究

李晨朋，韓 印，王馨玉

（上海理工大學管理學院，上海 200093）

0 引言

目前，社會車輛的車載數據可利用率很低，但是基于公交聯網的城市公交運行控制技術非常成熟，這項技術在獲取公交車輛ID、本地時間、位置、速度、加速度等方面十分便利。在由公交智能車載單元系統、智能路側系統和中心監控平臺系統組成的車聯網環境下，實現對道路交通狀態的估計，可為公交優先控制提供依據，對研究道路運行情況具有重要的意義。

忽略社會車輛的公交優先控制，會使道路上車輛的擁堵情況加劇。利用車聯網系統對公交背景交通狀態進行估計，以總體交通狀態進行實時公交優先控制，是降低對社會車輛影響的有效方法[1]。目前，許多國內外學者已經對車聯網系統和交通狀態估計進行了研究。隨著網絡技術的不斷發展，車路協同系統中的車聯網技術可為交通數據采集和分析提供先進的方法[2-5]。已有的對車聯網系統的研究，一部分是基于對車聯網系統采集的數據信息進行建模求解的研究[6-8]；另一部分是借助聯網公交車對車聯網系統進行深層次、精細化的應用[9-10]。現有的對交通狀態估計的研究，有的基于傳統的固定線圈進行交通狀態估計[11-12]；有的通過改良算法提高交通狀態估計準確率[13-14]；另外，以密度和速度來估計交通狀態，得到了國內外學者越來越多的認可[15]。然而上述研究主要是對交叉口的狀態進行估計和研究，并未對交叉口上游及周邊路段狀態進行深入又精確的研究，不利于從路網整體出發改善交通運行情況。

因此，在聯網公交車和社會車輛混合行駛的道路環境中，本文結合了公交車的車聯網系統和傳統道路感應線圈的各自特點，利用車聯網技術對公交車實時速度數據進行采集，建立了道路交通狀態的線性變參模型；利用感應線圈為卡爾曼濾波算法提供相關參數，對模型進行求解，實現對公交車輛背景交通狀態的估計和實時更新。為了驗證交通狀態估計結果的有效性，引進了誤差指數，并通過道路真實數據進行了仿真測試。為了進一步提高準確性，結合歷史數據提出了狀態估計修正模型，通過與原始估計結果的對比得出了研究結論，該結論可以為科學實施公交優先策略提供參考。

1 模型建立與算法求解

1.1 交通狀態估計基本模型

首先，基于交通密度動態特性建立線性參數可變（Linear Parameter-Varying，LPV）系統，將道路分為i個路段。然后，考慮路段上時間步長t的密度ρ(t)是由路段上的車輛數除以路段長度Δi得到的。動態密度可以用下面的時間離散方程來描述：

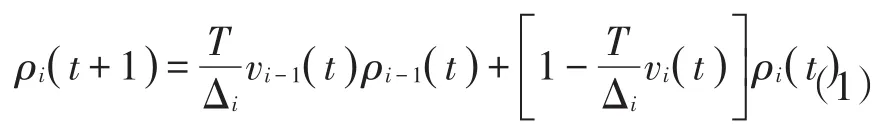
式（1）中：ρi(t+1)為i路段在t時間下一時刻的密度（veh/km），i為路段編號，i=1,2,3,…,N；T為時間離散的步長（h）；Δi為路段i的長度（km）；vi(t)為i路段上t時刻的車輛平均速度（km/h）。

為了使式（1）的時間離散關系足夠精確，即在現實情況下，路段上駛出的車輛數不能超過路段上原有的車輛數，式中系數不能為負。假設社會車輛的平均速度與公交車輛的平均速度大致相等，那么基于公交車的車路協同系統，vi()t是可以直接測量得到的，因此定義交通狀態為密度的矩陣，則根據式（1）路段的動態密度，交通狀態可以表示為線性變參數系統，即LPV系統：

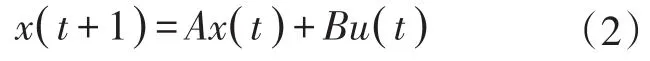
式（2）中：x(t+1)為t+1時刻系統狀態估計矩陣；A為隨時間變化的動態參數；x(t)為t時刻的狀態矩陣；B為路段性能參數；u()t為狀態的控制變量矩陣。這些參數的具體定義如下：

式（3）中：j是公交車到達的路段編號。

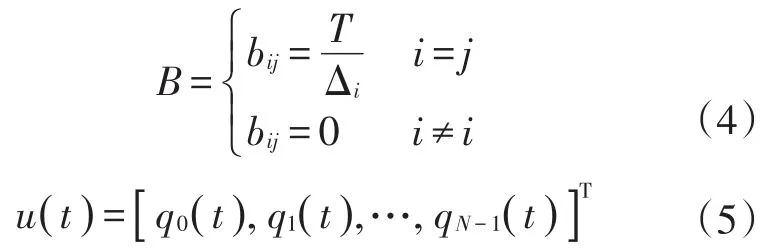
式（5）中：qi是道路路段的檢測流量（veh/h）。

LPV系統是一類研究線性時變的系統，其動態變化是由于某些參數發生了變化。對于系統需要的測量值，假設在道路路段的出口處，通過固定流量檢測器可以得到流量qi，通過公交車載系統得到平均速度vi，密度的測量值ρi也可以通過反推計算得到。

1.2 卡爾曼濾波算法工作原理

對于卡爾曼濾波算法，離散型過程控制方程是必不可少的。在本文中以一個線性隨機微分方程（Linear Stochastic Difference Equation）來體現：

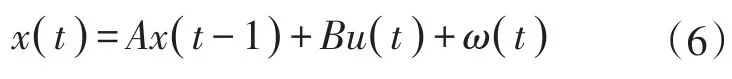
式（6）中：ω(t)為估計系統狀態過程中的噪聲矩陣。

然后需要對估計系統的測量值進行定義：

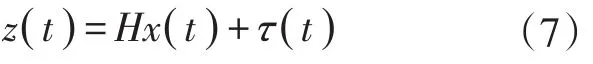
式（7）中：z(t)為t時刻測量密度的矩陣；H為線圈檢測器的參數，在檢測系統與估計系統不統一的情況下，H為矩陣；τ(t)為系統的測量噪聲。ω(t)和τ(t)需要為高斯白噪聲（White Gaussian Noise），并把它們的協方差定義矩陣為Q,R。

很顯然，前文提到的交通估計的線性變參數模型滿足上面的條件，所以卡爾曼濾波算法是最滿足需求的。接下來，要利用交通狀態估計模型來估計下一時刻交通流的狀態。根據所提出的交通狀態估計模型，基于道路的前一狀態可以初步估計出當前狀態。系統狀態的估計結果更新后，要對初步估計時刻的協方差矩陣進行同步修改：

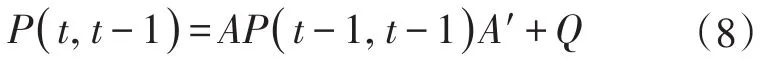
式（8）中：P(t,t-1)為t時刻初步估計對應的協方差矩陣；P(t-1,t-1)為t-1時刻對應最終估計的協方差矩陣；A′為A的轉置矩陣；Q為交通狀態估計過程中的協方差矩陣。

如此便完成了對系統狀態的初步估計，有了狀態的初步估計結果后，還要采集現在時刻的測量值。結合初步估計值和測量值，可以得到t時刻的最終估計值x(t,t)：

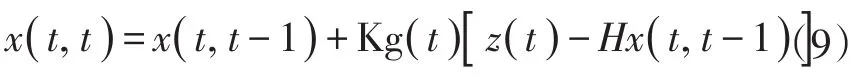
式（9）中：Kg為卡爾曼增益(Kalman Gain)矩陣。

如此一來，便得到了t時刻最終的估計矩陣x(t,t)。最后能讓卡爾曼濾波器不斷迭代下去的前提條件是，根據卡爾曼增益矩陣對t時刻下x(t,t)的協方差矩陣進行如下更新[16]：

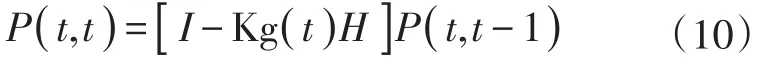
本文為單模型單測量，故式（10）中I為單位矩陣。

依據上述系列公式即可得到狀態估計矩陣，完成對下個時刻狀態的估計，也可以迭代估計n次，完成n個時刻的狀態估計。

1.3 交通狀態估計結果修正

為了使估計結果更加接近路面真實情況，根據歷史數據對交通狀態估計結果進行修正，可采用相對應的2d中對應時刻的交通狀態差值作為交通狀態估計過程的修正量，即：

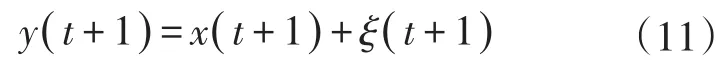
式（11）中：y(t+1)為t+1時刻修正后的狀態估計矩陣；x(t+1)為t+1時刻的狀態估計矩陣；ξ(t+1)為t+1時刻對應的修正量的矩陣。

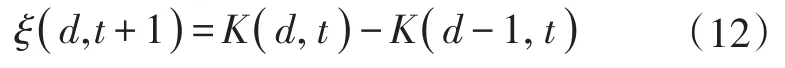
式（12）中：d為進行狀態估計的日期，d-1為上一個對應日期；K(d,t)和K(d-1,t)為第d天和第d-1天t時刻的實際狀態矩陣。

2 實驗與分析

2.1 狀態估計方法的評價指標

為了評估估計結果，使用以下反映誤差的指標，即地面真實密度ki與估計密度ρi的誤差指數（Coef?ficient of Variation,CV）[17]。在進行仿真測試結果分析時，如果數據的變異系數大于15%，則該結果不滿足需求，應該對模型進行進一步修正。誤差指數計算公式如下：

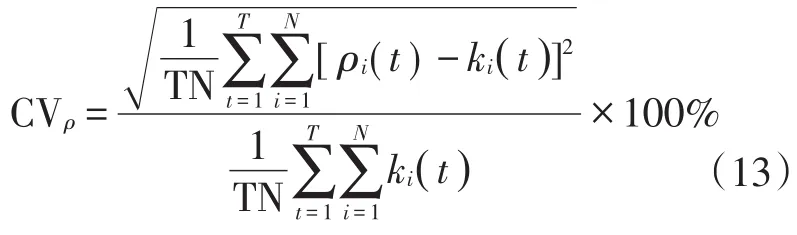
2.2 建立仿真測試平臺

為了檢查估計方法的有效性和準確性，運用微觀交通仿真軟件Vissim，以上海市軍工路和翔殷路兩條道路交叉口以及附近相鄰交叉口及其附屬路段組成基本路網。上游的流量數據隨著某些參數反饋到微觀模型上；具體的流量測量情況通過仿真軟件Vissim模擬生成，真實值是通過實際觀察得到的數據，其參數已經進行了適當調整。得到輸入數據后，利用卡爾曼濾波進行預期的交通狀態估計，它是道路實況的估計值。在通過微觀仿真軟件得到系統所需輸入數據后，利用Matlab軟件，實現所提算法對模型的求解。

考慮到模擬包括常規車輛和公交聯網車輛的混合交通情況，本文將評估在各種公交聯網車輛占有率下的估計方案的性能。為了考慮各種當前和未來可能出現的交通情況，設置流量由低到高、密度由小到大的交通環境條件，評估各種公交聯網車輛占有率的交通狀態估計方案，特別是0.5%,1%,2%,5%和10%占有率下的交通狀態估計性能[20]。鑒于微觀模型參數（如需求、目的地和車輛屬性）是隨機的，本文設計在5種交通環境條件下分別模擬每個占有率的狀態估計性能，平臺使用參數如表1所示。值得一提的是，在表1中，觀測噪聲和系統過程噪聲都比較大，這是為了使初始值遠離實際值，以此來驗證所提算法的高效性和準確性。

表1 平臺參數設置

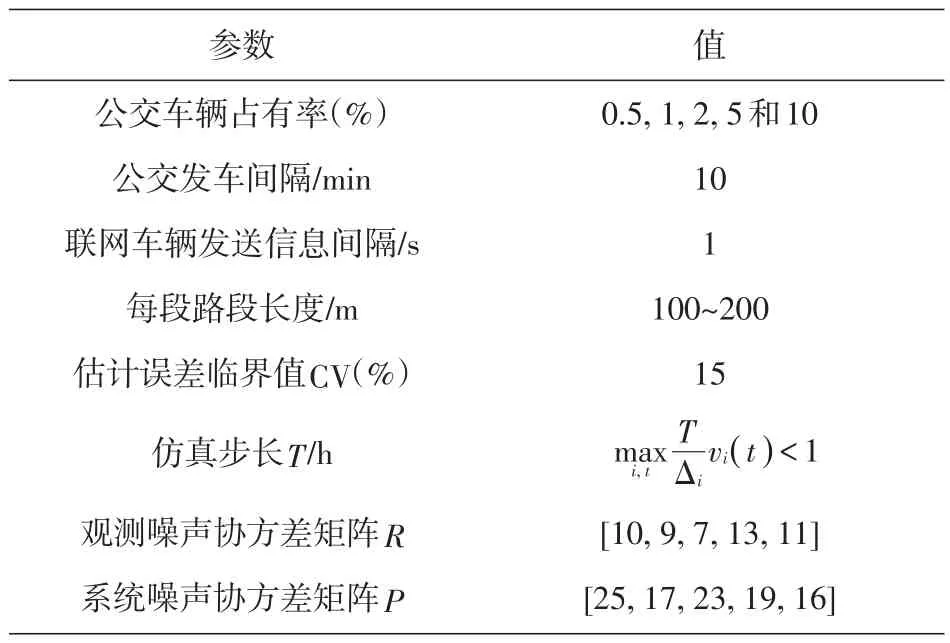
表1 （續）

2.3 仿真測試結果分析

本節對狀態估計模型和估計修正模型分別進行仿真求解并對比各自的交通狀態估計結果，采用式（13）的誤差指數對狀態估計結果進行評價，從交通環境條件、占有率和誤差優化性能3方面來證明所提方法的優勢，誤差指標計算結果見圖1。

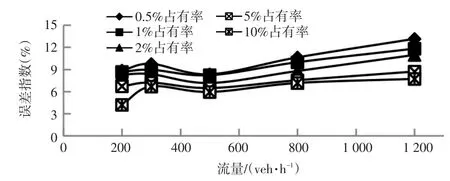
圖1 狀態估計誤差指數

由圖1可以看出，流量為200veh/h,300veh/h,500veh/h,800veh/h和1 200veh/h的同一條道路的5種交通環境條件下，即從自由流到擁擠流的交通環境下，基于卡爾曼濾波算法的狀態估計的誤差指數均不超過15%。該結果證明了交通狀態估計模型在所有占有率情況下都能獲得很好的狀態估計性能。在各種占有率條件下當流量不超過800veh/h時，狀態估計的誤差指數均不超過11%。該結果驗證了在此類交通環境條件下狀態估計的準確性。尤其在流量為500veh/h時，狀態估計的誤差指數出現明顯下落，各個占有率的跌幅在1%左右，進一步驗證了在此交通環境下，估計性能較好。當流量超過800veh/h，車流產生大幅擁擠波動，致使誤差指數再次開始回升，但是并沒有超出理想預期。直到流量到達1 200veh/h，最大誤差指數達到13%，仍未超過15%這個誤差偏離極限。該結果證明了狀態估計結果的有效性和適用性，即便在交通環境條件復雜的情況下，結果也是令人滿意的。不僅如此，即使占有率低至0.5%，得到的結果依舊讓人滿意。值得注意的是隨著占有率的增加，系統的性能不斷提升。尤其是當占有率達到5%時，系統性能的提升更加明顯，而且系統的性能提升量接近峰值；而在這個占有率之后，系統性能的提升效果趨于平緩，直到道路上的車輛均為聯網車輛。從經濟效益的角度來說，5%左右的占有率是一種節約成本、效益較高的臨界占有率。

為了進一步提高狀態估計模型的準確性，更好地反映真實道路狀態，本文基于卡爾曼濾波算法的特性，對狀態估計模型進行了更深層的修正。為了確保交通狀態估計修正模型與交通狀態估計模型具有可比性，本組實驗依舊以之前的仿真平臺為基準，設置相同的占有率、交通環境條件等微觀仿真參數。另外，加入了基于歷史數據的交通狀態修正量，對修正模型進行Vissim仿真和Matlab求解。最終得到了在低、中、高3種道路流量代表的交通環境條件下，狀態的估計值、狀態估計的修正值和誤差指數，以此作為特設估計方案。具體來說，就是以200veh/h,500veh/h和1 200veh/h 3種道路流量分別代表流量較小、中等流量和流量較大3種交通環境條件，誤差指數結果如圖2所示。

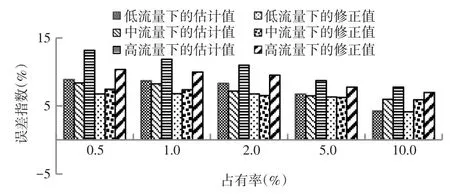
圖2 估計值與修正值的誤差指數

根據圖2顯示的結果，對比修正前后的狀態估計值的誤差指數。在各個占有率和交通環境條件下，修正后狀態估計值的誤差指數均有明顯下降。該結果證明了狀態估計修正模型更能反映真實道路狀態。在流量較小的交通環境條件下，未修正的狀態估計值誤差指數平均為7.36%，而修正后誤差指數平均下降了2%。在中等流量的交通環境條件下，雖然未修正的狀態估計的誤差指數相對較小，平均誤差指數僅為6.94%，但是修正后誤差指數也平均下降了1%。在流量較大的交通環境條件下，誤差指數下降明顯，未修正的狀態估計值誤差指數平均為10.49%，修正后誤差優化量達到了3%。該結果證明了狀態估計修正模型不受限于交通環境條件的劇烈變化，即使交通環境條件比較復雜，也能有很好的適用性。為了更加直觀地反映狀態估計修正模型縮減誤差的性能，根據仿真結果，對比狀態估計修正模型和未修正的狀態估計模型的狀態估計誤差指數，最終得到了誤差優化的具體情況，如圖3所示。

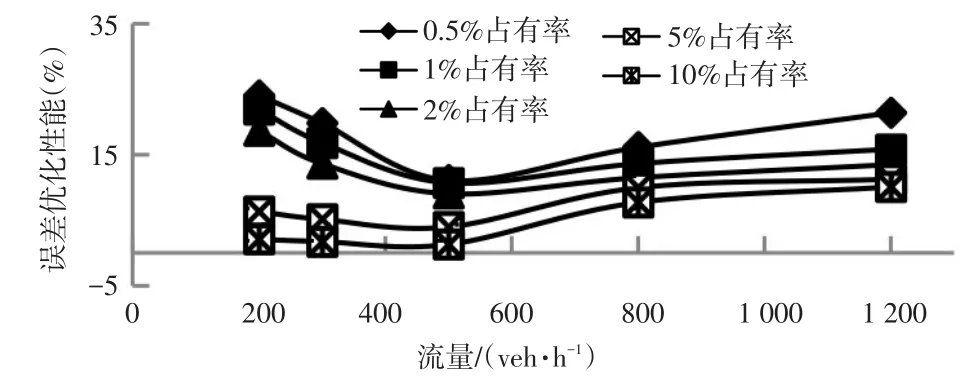
圖3 修正模型的誤差優化性能

根據圖3顯示的結果可以清楚地看出，總體上狀態估計修正模型能更好地優化誤差。在各個占有率和各種交通環境條件下，誤差優化性能均能有較為明顯的提高。具體到各個占有率中表現出：在占有率較小的情況下，誤差優化性能較好，最大優化性能達到了25%，最小優化性能也有令人滿意的10%左右；在占有率提高到2%以上后，誤差優化性能變化較為平和，平均優化性能在8%左右，進而驗證了狀態估計修正模型得到的結果更加接近真實情況。具體到各種交通環境條件中表現出：當交通流量低于500veh/h時，修正模型的估計誤差優化性能慢慢減小；而當交通流量超過500veh/h后，修正模型的估計誤差優化性能又開始慢慢提升。因此可以看出，在交通流為自由流和不穩定流兩種情況下，狀態估計修正模型發揮了很大的作用，誤差優化性能分別為14.57%和14.39%；在交通流為穩定流的情況下，誤差優化性能在10%左右。在所有占有率和交通環境條件下，交通狀態估計修正模型的系統總體誤差優化性能為11.87%，有非常大的提升。

綜上所述，在各種占有率和交通環境條件下，狀態估計模型的估計結果是有效的。不僅如此，模型對估計過程中的系統誤差和測量誤差是十分不敏感的，可以很好地消除估計和測量過程中的誤差。隨后，在對基于卡爾曼濾波的修正模型進行狀態估計時，狀態估計的誤差相比之前會大大縮減，極大地提升了狀態估計性能。

3 結論

本文利用聯網公交車輛的實時動態速度，建立了密度的動態時間離散模型。基于卡爾曼濾波對模型進行求解，實現了對道路路段交通狀態的估計，并借助歷史數據對模型進行修正，進而提升了對交通運行狀態進行估計的準確率。所用的交通狀態估計模型雖然在估計過程中存在一定的系統誤差和測量誤差，但不影響模型的準確性和有效性。交通狀態估計修正模型的優良性能，主要體現在對原有模型估計結果存在的誤差的進一步縮小，表現出了更好的準確性和適用性，使得狀態估計方案更加具有實際應用意義。下一步可研究更大時間跨度的交通狀態估計，并探討突發的特殊交通狀態對模型性能的影響程度等。