鋼筋混凝土框架結構柱端屈服影響因素的識別

高環 付明琴 張雪潔

（武昌工學院土木工程學院 武漢430065）

引言

2008年汶川地震震后發現鋼筋混凝土框架普遍出現的是柱鉸機制[1，2]，未能實現抗震設計所預期的“強柱弱梁”屈服機制。國內學者針對該問題進行分析，討論了現澆樓板、填充墻、框架梁端超配、大震下結構受力狀態與彈性受力狀態的差異等因素的影響[2]。文獻[2，3]均提到了結構在罕遇地震作用下實際受力狀態與截面設計階段彈性受力狀態的差異這一影響因素，其中文獻[3]認為柱端過多形成塑性鉸的一個重要原因是非彈性動力反應過程中由于結構構件各部位以及各樓層的非彈性性能發育程度有較明顯差異，導致在交替側向變形過程中構件之間和各樓層之間會出現內力重分布，于是會出現各樓層之間不同柱段內反彎點不斷發生隨機性移位。同一框架柱在彈塑性階段的反彎點發生了隨機性移位，有可能使一端柱端實際作用彎矩明顯大于屈服彎矩，從而使該柱端出現塑性鉸。關于這一因素對柱端屈服的影響，雖在相關文獻中均有提及，但均未作深入研究。

在各國規范提出的“強柱弱梁”措施具體規定中，只有新西蘭規范NZS3101（1995年版的附錄A方法和2006年版的方法A）考慮了由于高階振型的影響造成的非彈性反應分析彎矩與靜力分析的差異，其參考文獻[4]以12層框架柱非線性動力分析（分析用“柱模型”完成）得到不同時點的彎矩圖與等效側向靜力分析的對比，可以看出彈塑性反應階段反彎點移位較明顯，而出現反彎點移位較明顯對柱端出現塑性鉸的影響則缺乏研究依據。

基于以上提到的背景，本文以高烈度區（8度0.2g區和9度0.4g區）的典型空間框架KJA、KJB為例，為降低計算結果處理的復雜性和提高非線性反應的規律性，對所建立的非線性分析模型均只考慮朝H2方向輸入單向地面運動，即進行擬三維分析。對所分析的框架在各條地面運動輸入下，重點分析每根柱子屈服時段內（該框架柱至少一端出現屈服的時間內）反彎點高度（下文均以反彎點實際高度與柱高的比值呈現）特征；此外，由于地震作用引起的傾覆彎矩會造成柱內軸力的較大變化，尤其對邊柱影響較大，對于處于大偏壓狀態的框架柱而言，軸力變小時屈服彎矩相應變小，從而可能影響柱端提前出鉸。因此，軸力對邊柱的屈服影響進行識別。

1 算例信息

本文按照《混凝土結構設計規范》（GB 50010-2010）[5]和《建筑抗震設計規范》（GB 50011-2010）[6]設計的兩個分別位于8 度0.2g區、9度0.4g區的框架結構KJA、KJB，抗震等級分別為二級、一級，場地類別均為Ⅱ類場地，抗震分組均為第二組，均設定為丙類商場建筑。框架具體信息見表1，框架桿件編號見圖1，平面布置見圖2。

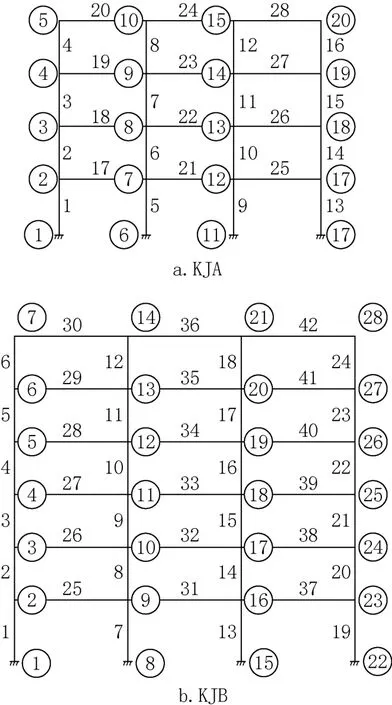
圖1 算例框架的桿件編號Fig.1 Frame number of KJ example

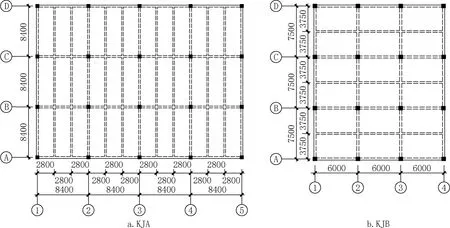
圖2 算例框架KJA、KJB結構平面布置 （單位：mm）Fig.2 Planes of frame structures KJA，KJB （unit：mm）

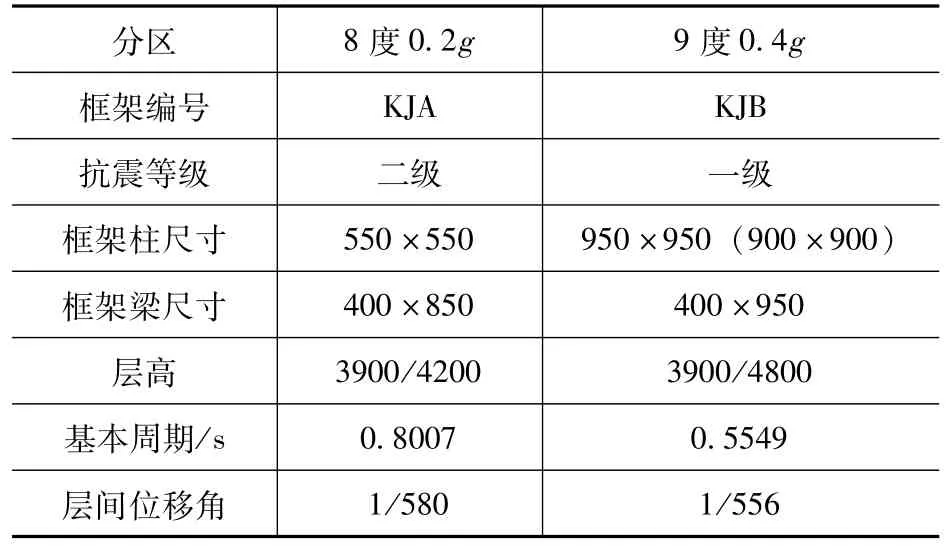
表1 算例框架基本信息Tab.1 Details of the frame structures

兩個框架荷載信息一致，外墻折算線荷載為16.2kN／m，女兒墻折算線荷載為7.6kN／m，樓面恒荷載為4.0kN／m2，屋面恒荷載為5.5kN／m2，樓面活荷載為3.5kN／m2，屋面活荷載為2.0kN／m2，基本風壓為0.30kN／m2，地面粗糙度類別為C類。

2 彈塑性建模及構件端部屈服判別

2.1 框架的彈塑性建模

基于文獻[7]的研究，本文選擇PERFORM-3D軟件進行彈塑性分析，構件模擬選擇由纖維段來模擬塑性區模型，纖維段內材料的模擬分約束區和非約束區，由于判別構件端部屈服所用的XTRACT軟件中使用的混凝土為Mander模型，故混凝土本構模型采用Mander模型。鋼筋選用理想彈塑性模型。

現澆樓蓋采用彈性殼單元來模擬。本文算例中根據文獻[8]建議將梁側6倍板厚內板筋加入梁截面的頂部縱筋纖維中，以便考慮有效翼緣寬度范圍內與梁肋平行的板筋對梁截面負彎矩抗彎能力的貢獻。

2.2 地面運動選取

本文針對兩模型KJA、KJB分別選取了7條單向地面運動，這些地面運動均來源于美國太平洋地震工程研究中心網站上公布的地面運動數據庫NGA-WEST 2。本文采用雙頻段選波方法，具體過程見文獻[9]。由于各國規范規定普通結構沿兩主軸方向分別進行設計，為與其呼應，本文非彈性動力反應分析選用單向地面運動沿結構一個平面主軸方向輸入，本文算例地面運動輸入方向為H2向。所選地面運動信息見表2。

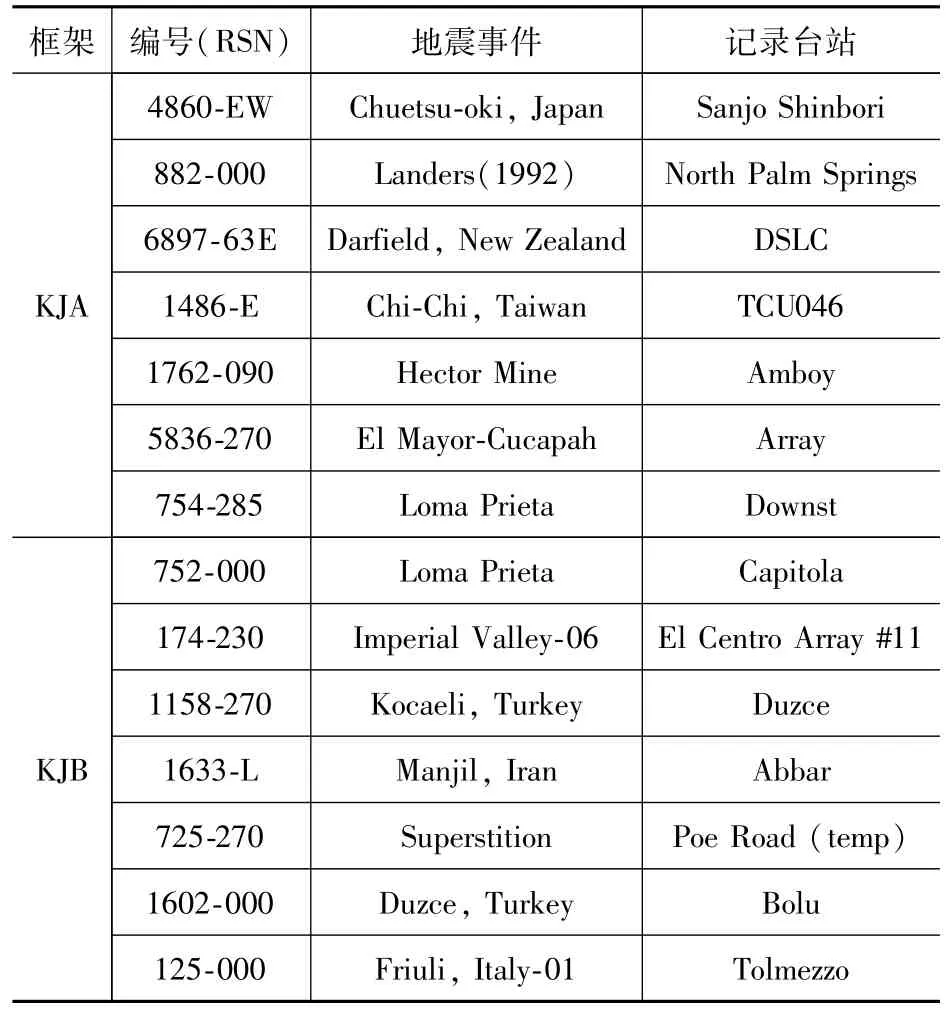
表2 各條地面運動的基本信息Tab.2 Basic information of earthquake ground motion records

2.3 構件端部屈服判別方法

由于PERFORM-3D軟件針對纖維模型可以提供的端部纖維某時點的最大拉壓應變是此時點之前達到的最大應變，而不能提供每個時點的具體應變值，故本文擬采用XTRACT截面分析程序得到截面的屈服彎矩時程來判斷柱截面每個時點的屈服狀態。

本文判斷柱端截面在整個時程中每個時點屈服狀態的方法是：根據XTRACT建立該柱截面的纖維模型，進行P-M分析得到柱截面的Ny-My曲線。再根據非彈性分析得到的該柱截面的軸力和彎矩時程，每一時點的彎矩與此時點軸力對應的My比較即可判斷截面是否屈服。

通過以上方法判斷的柱截面初次屈服時刻與通過PERFORM-3D軟件提取該截面最大拉應變時程得到的截面初次達到屈服應變的時刻相吻合，證明所提出的方法是可行的。

判斷梁截面屈服時，由于梁截面軸力較小，一般忽略不計，故梁的屈服軌跡是一個定值。具體確定梁端My的方法為：利用XTRACT建立梁截面的纖維模型，進行M-φ分析，XTRACT可以實現材料應變和截面內力兩個層次來輸出結果，從而可以識別鋼筋纖維拉應變達到2.278×10-3時對應的彎矩作為My。由于梁截面一般不是對稱配筋，一般頂部多于底部，故梁截面有負彎矩屈服能力和正彎矩屈服能力。

3 算例框架的非彈性分析結果

3.1 非彈性反應過程中柱子反彎點移位對柱端屈服的影響

各條地面運動輸入下各樓層柱子屈服時段內反彎點高度的分布散點圖如圖3所示（由于篇幅限制，以KJA在RSN4860輸入下柱屈服時段內反彎點高度特征為例，其他結果保持一致）。

對比KJA在所選7條地面運動輸入下各層柱在屈服時段內反彎點高度分布圖，有以下規律：底層柱子屈服時段內反彎點必定在柱高中點之上，這是因為基礎對于柱底的約束不變且比作為底層柱子上部約束的一層梁約束要強；二、三中間層柱子屈服時段內反彎點分布高度均在中點左右，頂層柱子反彎點高度處于中點以下，進行細部考察后發現此時段內頂層梁均未屈服，則作為頂層柱子的上端約束不變，作為頂層柱子的下端約束在此時段內屈服而約束相對較弱。KJB在所選7條地面運動輸入下，各層同一柱在各條地面運動輸入下在屈服時段反彎點高度分布區間集中。

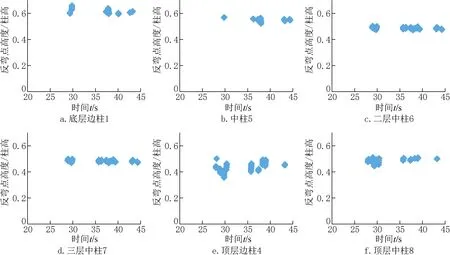
圖3 KJA在RSN4860輸入下各層柱在屈服時段內反彎點高度分布散點圖Fig.3 The distribution of the height of the point of contraflexure during the column yielding period under RSN4860 in KJA

柱子反彎點是柱上下端彎矩大小的相對比例的標志，在非彈性反應過程中反彎點高度在不斷變化，但是柱子屈服時段均不發生在柱子反彎點極低和極高時點。框架設計采用PKPM設計，查詢SATWE計算結果得到，第一振型基底剪力貢獻達到82%，可以認為本算例中框架的振動是以第一振型為主，而且柱端屈服時刻均是在地震力較大的時刻，故柱端屈服時段內反彎點高度不會極低或極高。

本文從兩個方面來討論柱子反彎點所揭示的柱子屈服規律。一方面，柱子未出現塑性鉸時，層間側移較小，由于地震作用較小且大小和方向不斷隨機變化，此時與豎向荷載組合形成的柱端彎矩的大小和方向則不斷變化，此時反彎點僅僅是上下端彎矩相對大小的一個比例而已。另一方面，柱子出鉸時刻均是層間位移角較大的時刻，此時地震作用較大，豎向荷載作用下柱端彎矩與較大的地震力下的柱端彎矩相比較小可忽略，此時柱子端部彎矩可看作水平地震作用下的內力，而反彎點高低根據柱子上下端約束狀況不同而不同。故反彎點變化不是影響框架柱端屈服的主要原因。

3.2 邊柱內軸力對柱端屈服的影響

在地面運動輸入下的實際動力反應過程中，柱中軸力受水平地震作用引起的傾覆力矩所形成的附加軸力的影響，尤其是對邊柱影響較大，故主要分析邊柱內變化的軸力對柱端屈服的影響。本文定義柱子的實際屈服是一條曲線，屈服彎矩隨非線性分析中柱內軸力的變化而變化，按照彈性設計時柱處于大偏壓狀態，柱內軸力越大時其對應的屈服彎矩越大，軸力越小時屈服彎矩越小。在KJA中，如圖4所示，在RSN6897波輸入下，提取柱軸力時程，同時對應每一時點的軸力通過XTRACT進行的P-M分析得到對應的屈服彎矩時程。整個時程中，柱內軸力（軸力為壓力時取正號）最大為2842.83kN，最小為1276kN，相對應的屈服彎矩從1152kN·m到935.3kN·m。底層邊柱1內軸力最大值基本是最小值的兩倍多，相應的最大屈服彎矩是最小屈服彎矩的1.2倍多。

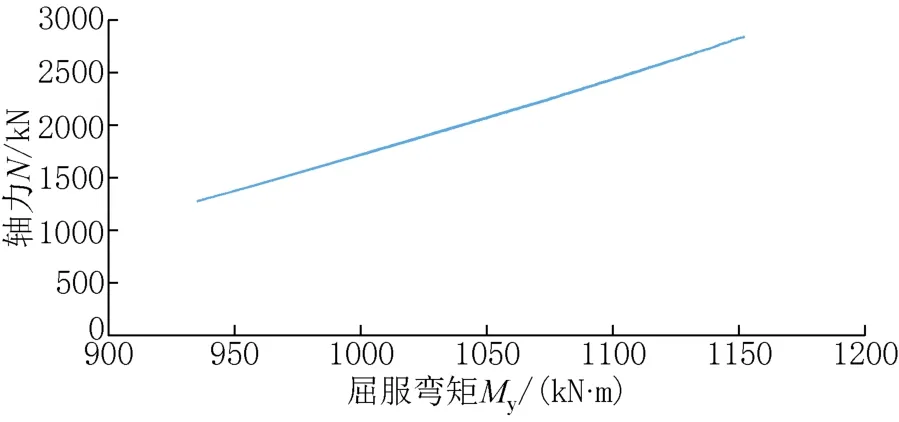
圖4 KJA的邊柱1在RSN6897波輸入下的實際軸力與屈服彎矩曲線Fig.4 The relationship between actual axial force and yielding moment of column 1 of KJA under RSN 6897

在各條地面運動輸入下，由于柱內軸力變化導致屈服彎矩變化從而影響柱子屈服狀態，圖5為KJA在各條地面運動輸入下的兩典型時點的受力狀態對比。

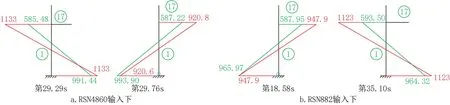
圖5 各條地面運動輸入下KJA兩典型時點的彎矩圖對比Fig.5 The comparison of moment diagram at two typical time points of KJA under each ground motion

圖5 中紅色為實際屈服彎矩，綠色為非線性分析彎矩。圖5a中在RSN4860波輸入下第29.76s時底層邊柱1出鉸，相比于第29.29s時柱1上下端截面作為作用方的非線性彎矩大小相近，方向相反是因為地震力反向導致的，第29.29s時底層層間位移角為負，此時由于水平地震作用所形成的附加壓力致使柱1軸力較大（-2693.64kN），到第29.76s時層間位移角為正，水平地震作用形成的附加拉力使柱1軸力減小至-1182.76kN，此時柱1的屈服彎矩也由1133kN·m減小至920.6kN·m，兩個時點狀態對比來看，作用方不變，但是由于軸力的變小使柱屈服能力變小導致截面出鉸。

圖5b中RSN882輸入下第18.58s由于水平地震作用引起的對柱1的附加拉力使柱1內軸力較小（-1361kN），此時柱1底部截面實際屈服彎矩為947.9kN·m，柱1底部出現塑性鉸。第34.10s時地震作用反向產生使柱1內軸力加大的附加軸力（軸力增至-2613.7kN），此時屈服彎矩也增大至1123kN·m，兩個時點雖作用相當，但是由于地震作用引起的附加軸力致使柱子屈服能力加大，從而未出現塑性鉸。

在其他5條地震波作用下底層邊柱在非彈性反應過程中的兩時點彎矩對比，同樣可得到由于軸力變化而屈服或者退出屈服狀態的規律（限于篇幅，本文只列舉了RSN4860和RSN882作用下的彎矩圖對比）。由于地震作用引起的傾覆力矩會造成邊柱內軸力變化較明顯，因此本文在此重點分析邊柱內屈服狀態。

圖5逐時點地揭示非線性反應過程中邊柱由于軸力的變化可以影響柱端的屈服，從單根框架柱這個層面上說，邊柱比同一樓層的中柱更容易屈服，但從非彈性反應過程形成的塑性分布格局來看，如圖6所示，邊柱卻均比同一樓層的中柱屈服程度偏小。這是因為平面框架內邊柱柱端與一根框架梁相連約束偏小，中柱柱端與兩根框架梁相連約束較強，而邊柱比中柱的作用彎矩偏小對以上不利因素起到“削弱”作用。故綜合來看，軸力不是邊柱柱端屈服的重要原因。

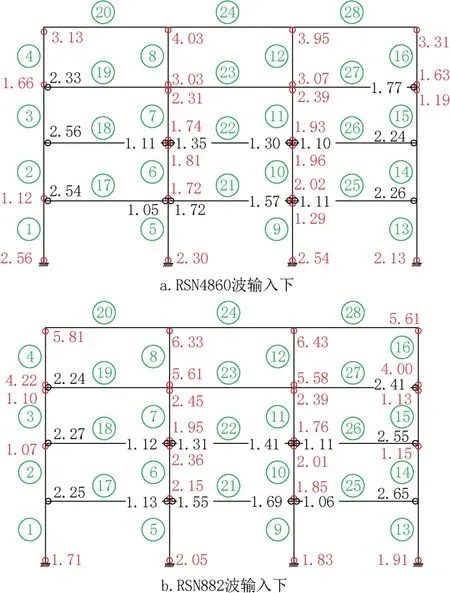
圖6 RSN4860、882輸入下KJA的塑性鉸分布Fig.6 The distribution diagram of plastic hinges under RSN4860、882 of KJA

4 結論

通過對8度0.2g區的二級框架KJA和9度0.4g區的一級框架KJB在所選的各條地面運動輸入下，通過對比各層柱屈服時段內反彎點高度分布散點圖和逐時點分析柱端屈服狀態圖可以得出：

1.通過對非彈性反應過程中同一框架柱在屈服時段內的反彎點高度進行細部識別和分析，得出反彎點隨機性移位不是造成該框架柱端過早出現塑性鉸的重要原因，反彎點過高和過低時均未出現塑性鉸，此時是由于變化較大的地震作用和相對較固定的豎向荷載下的內力組合的結果，而柱端出現塑性鉸時的反彎點對于同一框架柱相對較固定。

2.通過逐時點地對同一邊柱的彎矩變化識別以及塑性鉸分布格局得出罕遇地震作用下的樓層傾覆力矩所導致的一側邊柱軸力下降不是引起邊柱過早出現塑性鉸的重要原因。