一種能耗優先的WSN強柵欄覆蓋方法研究

方 凱，吳武豪，陳 瓊

（中電海康集團有限公司，浙江 杭州 310012）

0 引言

無線傳感器網絡柵欄覆蓋的主要作用是監測是否有監測目標發生入侵，如在軍事方面，將柵欄部署在陣地前沿能有效監測敵人是否發動突襲；在環保方面，將柵欄部署在工廠周圍能監測污染物擴散情況；在林業方面，將柵欄部署在保護區邊界可有效監測火災的蔓延等[1]。

目前在 WSN（Wireless Sensor Network）柵欄覆蓋領域已取得豐厚的研究成果，如在柵欄構建方面Saipulla（2013）等人提出一種基于線性部署的柵欄構建方法，沿目標路徑部署傳感器節點，從而提高了柵欄覆蓋的數量[2]。毛科技（2015）等人對傳統的蟻群算法進行改進使之適用于WSN柵欄構建問題，在部署區域內搜索存在的柵欄[3]。Wang Z（2017）等人考慮到利用WSN定位方法或GPS模塊獲得的節點位置信息存在誤差，提出一種位置容忍的柵欄構建方法，從而有效的解決節點位置不準確而導致柵欄構建不完整的問題[4]。Nguyen T G（2018）等人提出一種分布式的柵欄構建算法，利用網絡區域聚類技術減少節點間信息交換，通過移動少量可移動節點完成柵欄構建[5]。為延長柵欄的生存時間，柵欄調度算法被學者研究，如Kumar S（2017）等人提出了一種K-柵欄最佳調度算法，充分利用了傳感器節點的能耗，大幅延長了柵欄的生存時間[6]。Xu B（2016）等人通過構建入侵軌跡模型，預測柵欄中被頻繁攻擊的位置，并調度可移動節點強化這些位置，從而延長了柵欄的生存時間[7]。在柵欄修復方面的研究，如Deng（2013）等人提出了一種混合傳感器網絡柵欄間隙修復方法，通過調整傳感器節點的感知半徑，使可移動節點修復間隙的移動距離最短[8]。Chen J（2017）等人提出一種利用柵欄段旋轉方法修復柵欄間隙[9]。Xu H（2016）等人提出最小費用方案和自適應貪婪移動方案修復柵欄間隙[10]。

上述柵欄構建和柵欄修復方面的研究都取得了較好的成果，但這些方法對靜態節點的利用率不高，而對可移動節點的需求較大。考慮到成本以及柵欄構建、修復的代價問題，本文提出一種能耗優先的WSN柵欄覆蓋方法，該方法充分利用靜態傳感器節點構建和修復柵欄，如靜態傳感器節點不能完成柵欄構建或修復工作，再派遣少量的可移動節點，并且使可移動節點的移動距離最短，從而實現代價最小化。

1 相關模型

假設柵欄覆蓋的應用場景為理想場景，在節點部署區域中沒有障礙物的干擾，可移動節點都是沿直線移動，且傳感器節點采用電池供電，能耗有限。

在研究中傳感器節點采用二元感知模型，以傳感器節點為圓心，感知半徑為r，當監測目標在節點感知范圍內，則被節點感知的概率為1，否則為0，如公式1所示。

公式1中o表述傳感器節點位置，t表示監測目標位置，d（o，t）表示監測目標距離傳感器節點的歐氏距離，Po，t表示監測目標在位置t處被節點o感知的概率。

柵欄覆蓋可分為強柵欄覆蓋和弱柵欄覆蓋，本文研究強柵欄覆蓋，傳感器節點部署在帶狀區域中，監測目標沿任意路徑從帶狀區域的一側穿越到另一側至少能被一個傳感器節點感知，強柵欄覆蓋模型如圖1所示。

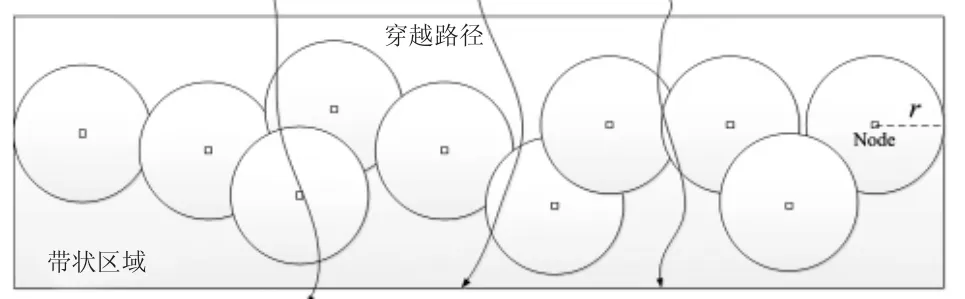
圖1 強柵欄覆蓋圖

在柵欄構建階段，主要能量消耗發生在可移動節點移動過程中，而在感知方面的能量消耗較少。參考文獻[11～12]研究了可移動節點移動能耗模型，由于節點在移動過程中消耗的能量遠遠高于感知所消耗的能量，且本文的衡量指標是節點移動所消耗的能量，因此節點感知的能耗忽略不計，移動1m消耗能量為3.6J。

2 柵欄構建方法

2.1 拓撲圖建立

靜態傳感器節點和可移動傳感器節點按一定比例隨機部署在帶狀區域中，且節點位置可通過WSN定位方法或GPS模塊得到，在構建柵欄過程中為充分利用靜態傳感器節點，盡可能降低可移動節點的需求量，采用靜態傳感器節點構建全連接拓撲圖，如圖2a）所示，圖中S為部署區域最左端節點，E 為部署區域最右端節點，di，j為節點 ni和 nj之間的歐氏距離。

在拓撲圖中從節點S開始到節點E結束，存在一條路徑，當該路徑被靜態節點和可移動節點完全覆蓋時，則完成了柵欄的構建。為了得到柵欄構建過程中不同路徑所需要的可移動節點數量，需要將全連接拓撲圖轉化為可移動節點需求圖，如圖2b）所示。

圖2 拓撲圖轉換過程圖

圖 2b）中 Mni，j表示節點 ni和節點 nj之間的邊被節點感知區域完全覆蓋所需要的最少可移動節點數量，如公式2所示。

式中：di,j——節點ni和nj之間的歐氏距離；

r——感知半徑。

2.2 最優柵欄構建路徑

圖2b）構建了部署區域內可移動節點需求圖，倘若存在一條路徑從節點S開始，到節點E結束，移動少量的可移動節點到該路徑上某些位置即可完成路徑的全覆蓋，則該路徑被稱為柵欄構建路徑。若構建柵欄過程中移動節點的移動距離總和最短，則該路徑為最佳柵欄構建路徑。

如果能夠在拓撲圖中尋找到最佳柵欄構建路徑，則構建柵欄的能耗會最低。影響柵欄構建能耗的因素有2個：①柵欄構建過程中需要移動的傳感器節點數量；②可移動節點的平均移動距離。由于傳感器節點隨機部署在區域中，因此并不能計算出哪條柵欄構建路徑構建柵欄的移動節點移動距離之和最短，但可以首先從因素①考慮，利用KSP[13～14]算法選擇需要可移動節點數量最少的前K條路徑，當K取值合適時，最佳柵欄構建路徑被包含在其中。如圖3所示，圖中利用KSP算法計算得到需要可移動節點數量最少的前3條柵欄構建路徑Path1、Path2、Path3，將可移動節點移動到待修復位置即可完成柵欄構建，其中Path1需要4個可移動節點、Path2需要5個可移動節點，Path3需要4個可移動節點。

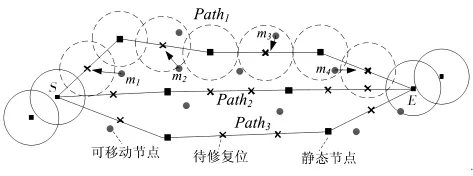
圖3 柵欄構建路徑圖

當確定K條柵欄構建路徑后，采用匈牙利算法虛擬派遣可移動節點到待修復位，并計算沿每條構建路徑完成構建柵欄可移動節點移動距離之和。匈牙利算法是一種最優指派方法[15][16]，假設指派a個工人完成a個任務，每個工人可以做多種工作，但是對每種工作的收費不同，利用匈牙利算法分配工作能使完成所有工作花費的代價最小。同樣的利用匈牙利算法派遣可移動節點完成柵欄構建能夠實現最優派遣，保證可移動節點的移動距離總和最短。本文對匈牙利算法進行改進使之適用于柵欄覆蓋問題。傳統的匈牙利算法需要a個人去完成a個任務，而在柵欄覆蓋問題上，派遣m個可移動節點去修復n個待修復位置，而m與n可能并不相同，如果m＞n，則虛擬出m-n個待修復位，可移動節點到虛擬待修復位的距離都為0；如果m＜n，則不能完成柵欄構建。如圖4所示，圖中總共有m1、m2、m3二個可移動節點，兩個修復位置1和2，因此需要虛擬出一個修復位置o，根據上述規則建立匈牙利算法的代價矩陣，如公式3所示。

圖4 匈牙利派遣圖

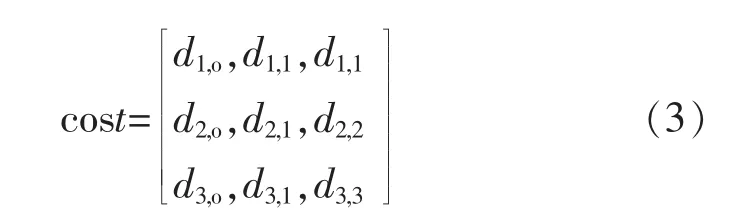
公式3中di，j表示傳感器節點距離待修復位的歐氏距離 （di，j≤R，R為可移動節點的最大移動距離），其中 di，o=0，表示節點距離虛擬修復位 o的距離都為0。

建立匈牙利算法的代價矩陣后即可計算出沿K條柵欄構建路徑構建柵欄可移動節點的移動距離之和，假設分別完成圖3中3條柵欄構建路徑可移動節點移動的距離總和為D1、D2和D3，且D1＜D2，D1＜D3，則 Path1是最佳柵欄構建路徑，沿該路徑構建柵欄消耗的能量最低。

2.3 柵欄構建過程

2.2小節從圖2b）可移動節點需求拓撲圖中選擇了最佳柵欄構建路徑，并采用匈牙利算法得到可移動節點最優派遣方式，因此本節根據派遣方案將可移動節點移動到最佳柵欄構建路徑的修復位置完成柵欄構建，如圖5所示。圖中可移動傳感器節點 m1、m2、m3、m4被派遣到最佳柵欄構建路徑上，完成柵欄的構建，且能夠保證構建柵欄時可移動節點的移動距離之和最短。

圖5 柵欄構建圖

3 柵欄間隙修復

柵欄運行一段時間后，由于傳感器節點能量耗盡或故障等原因導致柵欄出現間隙，監測目標可通過間隙穿越柵欄而不被檢測到，因此需要對柵欄間隙進行修復。修復方法與上述柵欄構建方法類似，首先定位到柵欄間隙的左右端，判斷柵欄中相鄰傳感器節點的感知區域是否相互重疊。如果不重疊，則判斷該處出現間隙，然后繼續尋找柵欄間隙的另一側，如圖6中柵欄出現了間隙，間隙最左側為L傳感器節點，最右側為R節點。定位到柵欄間隙后，以L節點為起始節點，R節點為結束點構建靜態節點全連接拓撲圖，然后將全連接拓撲圖轉化為可移動節點需求拓撲圖，最后利用匈牙利算法派遣可移動節點完成柵欄的修復工作。

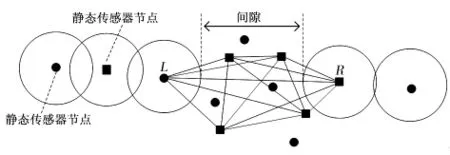
圖6 柵欄間隙圖

4 仿真實驗

采用i5處理器、8G內存的PC機，利用Matlab平臺進行仿真實驗。將靜態傳感器節點和可移動傳感器節點按照一定比例混合，隨機均勻部署在一個長為1000m，寬為200m的帶狀區域中，靜態節點和可移動節點的感知半徑r=50m，根據提出的方法構建柵欄如圖7所示。實驗分析了本文提出的方法的相關性能，并在柵欄構建方面與任勇默（2017）[17]等提出的FCOIS方法進行對比，在柵欄修復方面與 Saipulla A（2013）[18]等提出的 Optimal方法、貪婪算法（Greedy）進行對比。

圖7 柵欄構建結果圖

4.1 柵欄構建

部署區域確定的情況下，影響柵欄構建的因素主要包括傳感器節點數量、可移動節點與靜態節點的比例、傳感器節點的感知半徑r。評價柵欄構建方法的指標為可移動節點的能耗、柵欄構建率。實驗結果如圖8和圖9所示，實驗中可移動節點和靜態節點各占50%，可移動節點最大移動距離R=200m。

實驗結果表明，隨著帶狀區域內傳感器節點數量增加，構建柵欄時消耗的能量逐漸降低。因為部署傳感器節點數量增加，節點密度提高，構建柵欄時可移動節點需要移動的距離更短，因此能耗逐漸減低，且本文提出的方法在構建柵欄時的能耗遠低于FCOIS方法。因為本文的方法首先利用靜態傳感器節點構建柵欄，當靜態傳感器節點不能完成柵欄構建時，才移動少量的可移動節點完成柵欄構建；而FCOIS方法完全采用可移動節點構建柵欄，因此需要移動的節點數量遠多于本文方法。在傳感器節點數量為50個時，節約了971.6J能量，在傳感器節點為150個時，節約了426.5J能量。

圖8 柵欄構建能耗圖

在柵欄構建成功率方面，部署傳感器節點數量相同時，FCOIS算法的成功率高于本文方法。因為FCOIS完全采用可移動節點構建柵欄，因此節點具有較高的靈活性，能夠自由移動到任何指定位置完成柵欄的構建；而本文方法構建柵欄大部分采用靜態傳感器節點，倘若靜態傳感器節點部署位置比較集中，則可移動節點即使能夠移動較遠距離也不能完成柵欄構建。當傳感器節點數量為90個時，FCOIS方法的柵欄構建成功率達到100%，當傳感器節點數量為130個時（在部署區域內部署130個傳感器節點密度合適），本文方法的柵欄構建成功率達到100%。

圖9 柵欄覆蓋率圖

綜上實驗結果，本文提出的方法在柵欄構建方面，能夠節約大量的能耗，且當帶狀區域內部署的傳感器節點達到一定數量時，具有100%的柵欄構建成功率。

4.2 柵欄修復

Saipulla A （2013）[18]提出的 Optimal柵欄間隙修復方法首先定位到間隙所在位置，然后計算需要的可移動節點數量，最后采用二分法派遣可移動節點完成柵欄修復使得可移動節點移動距離之和最短。貪婪算法派遣最近的可移動傳感器節點修復柵欄。而本文提出的柵欄間隙修復方法首先尋找可以使用的靜態傳感器節點，當靜態傳感器節點不能完成柵欄修復時，派遣可移動節點修復柵欄。在帶狀區域中部署100個傳感器節點，可移動節點占30%，靜態節點各占70%，可移動節點最大移動距離R=200m，實驗結果如圖10和圖11所示。

由圖10可以看出，在柵欄間隙修復方面，隨著柵欄間隙長度的增加，二種柵欄修復方法修復柵欄的能耗呈梯度升高。因為柵欄間隙為50m和100m時需要的可移動節點數量相同，250m和300m需要的移動節點數量相同，因此消耗的能耗呈梯度提高。且本文的方法的能耗低于Optimal方法和Greedy方法，因為首先考慮使用靜態節點修復柵欄間隙，當靜態節點不能完成修復時，再派遣可移動節點，因此需要調度的可移動節點數量相對其他兩種方法較少，因此節點移動的總距離更短，消耗的能量更低。Optimal方法的能耗低于Greedy方法，因為Optimal方法使用二分搜索方法，能夠使派遣的可移動節點最優 （總移動距離最短），而Greedy方法每次都派遣距離待修復位置最近的可移動節點完成柵欄修復，會陷入局部最優問題，因此Greedy方法修復柵欄間隙的能耗高于Optimal方法。

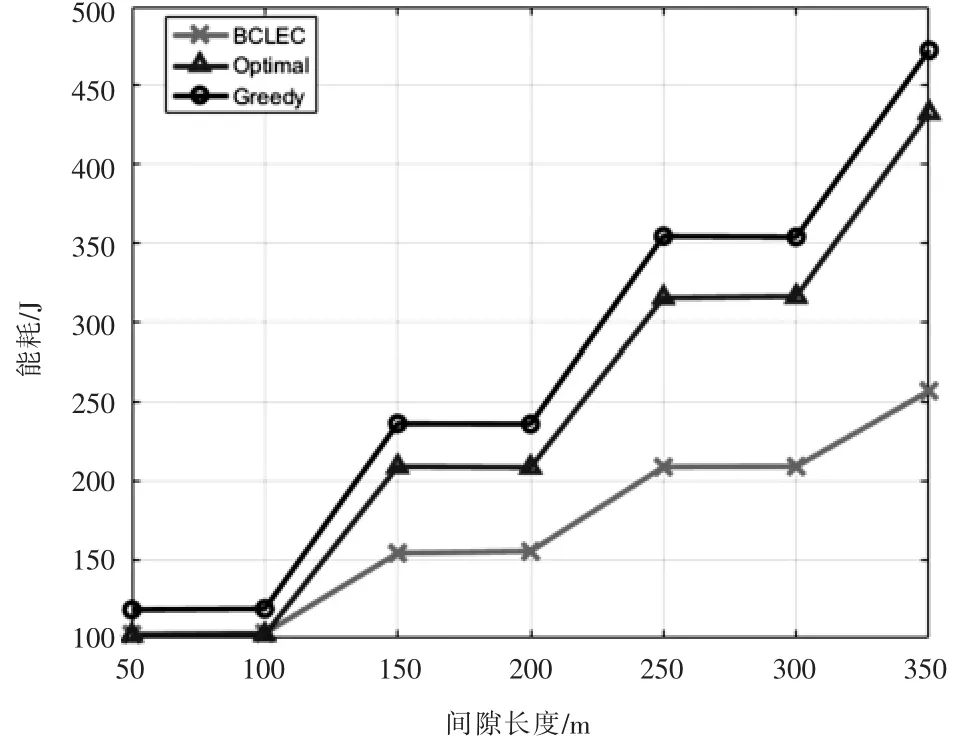
圖10 柵欄修復能耗圖

在柵欄修復率方面的實驗如圖11所示。實驗結果表明隨著柵欄間隙長度的增加，柵欄修復成功率會逐漸降低。因為柵欄間隙長度增加，需要的可移動節點數量增加，但可移動節點存在最大可移動距離R，故修復率逐漸降低。本文方法的柵欄修復成功率最高，在柵欄間隙長度為350m時，比Optimal方法提高了8%左右，比Greedy方法提高了12.6%左右，Optimal方法的修復成功率高于Greedy方法。

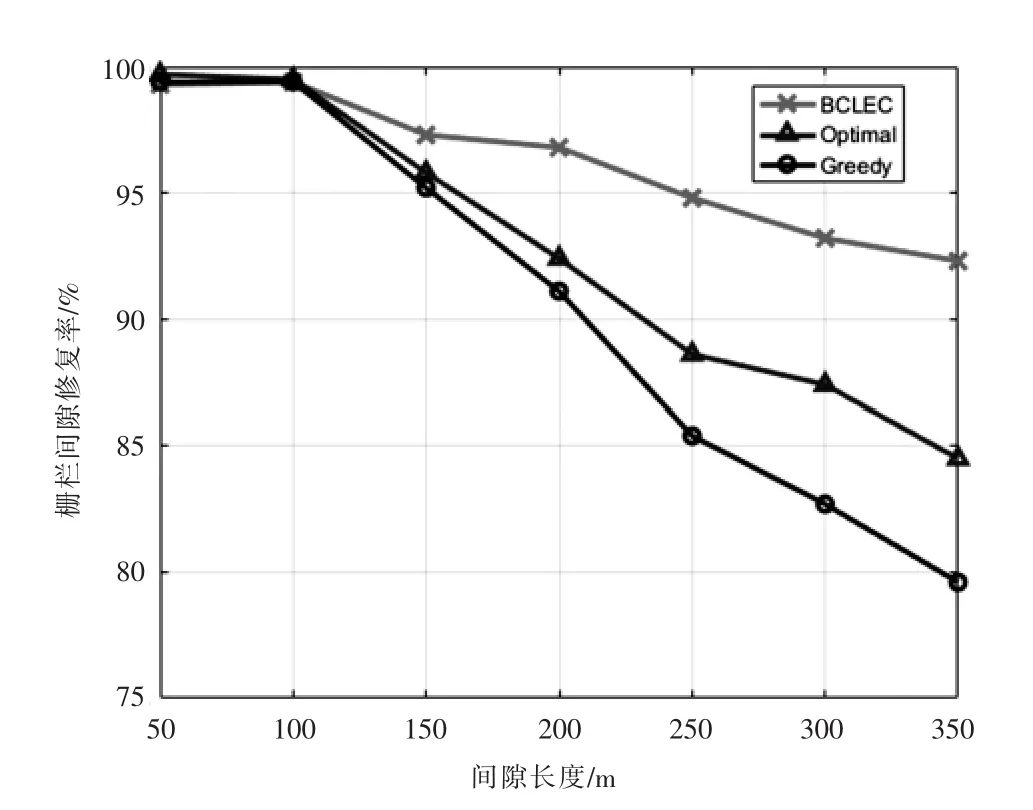
圖11 柵欄修復率圖

5 結語

本文研究了一種低能耗的WSN柵欄覆蓋方法，通過構建靜態節點拓撲圖，利用KSP算法和匈牙利算法構建柵欄使得可移動節點移動距離之和最小，即柵欄構建的能耗最小。然后提出了柵欄間隙修復方法，同樣利用前述算法支配可移動節點修復間隙，實驗結果表明該方法在柵欄覆蓋方面具有較好的性能。后續工作將進一步研究能耗最低的K-柵欄覆蓋方法。