兩軸速率轉臺U型架結構設計及有限元分析

安紅印

（河北漢光重工有限責任公司，河北 邯鄲 056000）

兩軸速率轉臺是導彈及航空航天領域進行半實物仿真和測試的關鍵設備，它可以模擬飛行器的運動姿態，廣泛應用于航空、航天及武器系統中。轉臺是一種高精度運動仿真和測試設備，它的力學特性的優劣直接影響其仿真和測試精度，是保證航空航天產品以及武器系統性能和精度的基礎。因此，在設計階段對轉臺U型架進行結構靜態和動態特性分析非常重要。

ANSYS軟件是融結構、流體、電場、磁場、聲場分析于一體的大型通用有限元分析軟件，它能與多數CAD軟件接口，實現數據的共享和交換，ANSYS軟件中得結構分析模塊包括靜力學分析和動力學分析，動力學分析又包括模態分析、諧響應分析、隨機振動分析、響應譜分析、瞬態動力學分析及線性屈曲分析。本文使用ANSYS軟件結構分析模塊對兩軸速率轉臺U型架結構進行靜力學和動力學分析。

1 轉臺的結構設計

兩軸速率轉臺是集光、機、電一體化的復雜系統。其結構形式多種多樣，主要有立式和臥式結構，其他結構都是在這兩種結構的基礎上衍生出來的。本文研究的兩軸速率轉臺采用立式U-O型結構，即外框架采用U型結構，內框架采用O型結構，該系統采用雙軸伺服控制系統，如圖1所示是兩軸轉臺的總體結構外形圖。U型架是轉臺的主要結構部件，它有支撐內框及負載的作用，因此U型架要有足夠的剛度、強度和盡可能小的轉動慣量。

圖1 兩軸速率轉臺結構圖

2 U型架的靜力分析

2.1 靜力學方程

結構靜力學分析是有限元分析中最基礎的分析方法。本文采用Ansys軟件對外框架進行靜力學分析，所謂靜力就是結構受到靜態載荷的作用，慣性和阻尼可以忽略，由經典力學理論可知，物體的靜力學方程為：

或

式中：[K]——總剛度矩陣；

{x}——節點位移矢量；

N——單元數；

{Ke}——單元剛度矩陣；

{Fa}——支反載荷矢量；

{Fr}——所受總外載荷；

{F}——力矢量。

通過式（1）可以得出{x}，由位移插值函數可以得出單元節點應變和應力的關系表達式：

式中：{ξel}——由應力引起的應變；

[B]——節點上的應變；

{ξth}——熱應變矢量；

{σ}——應力矢量；

[D]——彈性矩陣。

求解有限元方程式（4）和（5），即可得出單位各節點相對應的應力。

2.2 U型架網格劃分

ANSYS實體模型既可以在ANSYS環境中直接創建，也可以在CAD軟件中建模后再導入ANSYS環境下進行分析。本文是在Solidedge中建立實體模型，再將模型導入ANSYS中。兩軸速率轉臺的U型架材料選用鑄鋁合金（ZL114A），力學性能如表1所示。

表1 ZL1114A力學參數

網格劃分的疏密程度直接影響到計算結果的精度，但是網格加密會增加CPU計算時間和需要更大的存儲空間。理想情況下的網格密度是其計算結果不再隨網格的加密而改變。本例選用單元格尺寸（Element Size）為5mm進行劃分,劃分后的單元總數為71060個，節點總數為123176個，劃分結果如圖2所示。

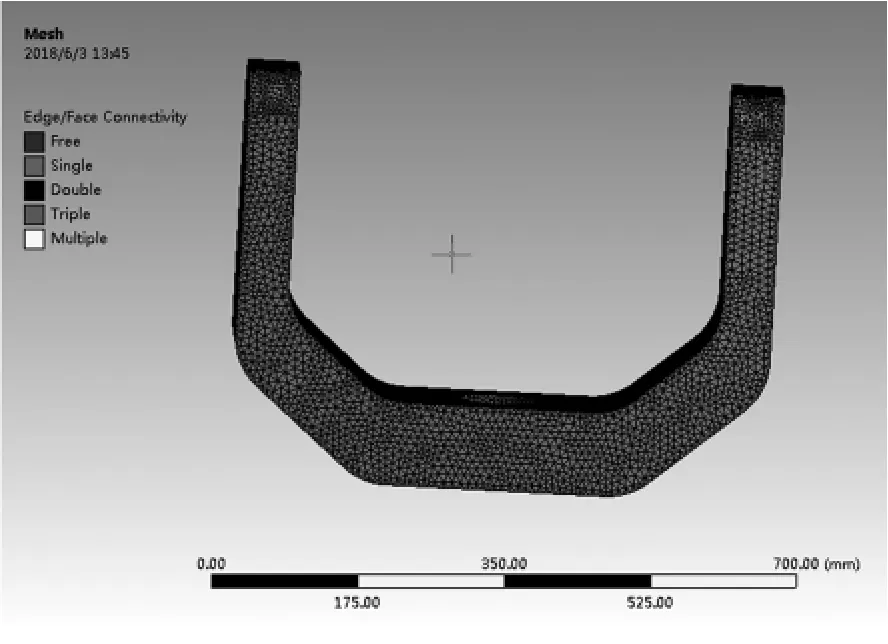
圖2 U型架網格劃分

2.3 添加載荷和結算結果分析

根據轉臺U型架的實際受力情況對其進行添加載荷和進行邊界條件的約束。添加的載荷主要有：①轉臺對U型架底面施加的約束，以限制底面的自由度；②U型架的自重和其上加載的負載對U型架施加的壓力；③模擬轉臺在運轉狀態下產生的慣性力矩。經計算，求解結果如圖3、圖4所示。

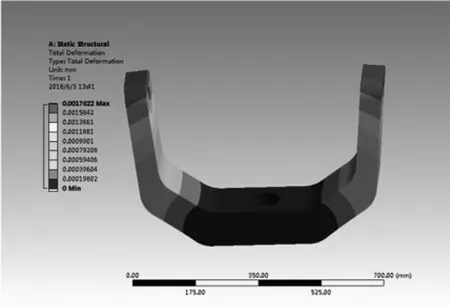
圖3 U型架位移變形云圖

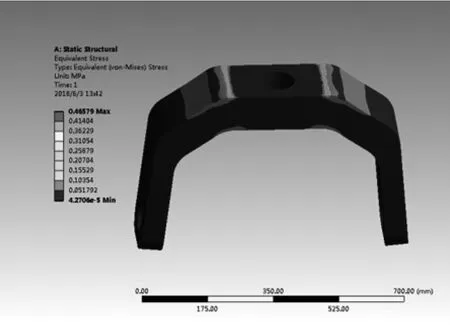
圖4 U型架等效應力云圖

由圖3可以得出，U型架結構在靜力載荷作用下得到的最大位移變形發生在U型架兩側的頂端，且最大位移量為1.78×10-3mm。因僅考慮在靜載荷作用下的位移變形，所以變形不大。由圖4可知，最大應力區出現在U型架底部棱邊處位置，最大應力σmax=0.47M P a，查表得 ZL114A的許用應力[σ]=230MPa,σmax＜[σ],故轉臺 U型架的結構設計能滿足強度要求。

3 U型架得動力學分析

3.1 動力學方程

動力學分析是用來確定慣性和阻尼起重要作用時結構的動力學行為的技術，典型的動力學行為有結構的振動特性，動力學分析可以模擬的物理現象包括：振動沖擊、交變載荷、隨機載荷地震載荷等。N階自由度系統的振動微分方程為：

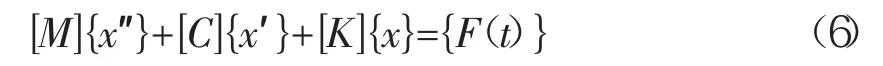
假設為自由振動并忽略阻尼時，其方程為：

結構的自由振動是簡諧振動，即位移為正弦函數

將（8）式帶入（6）式得

式中：[M]——質量矩陣；

[C]——阻尼矩陣；

{F（t）}——力矢量；

{x＇}——速度矢量；

{x″}——加速度矢量。

式（8）為經典的特征值問題，此方程的特征值為ωi2，其開方 ωi即自振圓頻率，自振頻率為 f=ωi/2π,特征值ωi對應的特征向量{x}i為自振頻率f=ωi/2π對應的振型。

3.2 模態分析

模態分析是計算結構振動特性的數值技術，結構振動特性包括固有頻率和振型。模態分析是最基本的動力學分析，也是其他動力學分析的基礎，模態分析可以獲取結構件的固有頻率和振型，從而使結構設計避免共振或者以特定的頻率進行振動。ANSYS中有7種模態提取方法，分別為子空間法、動態功率法、分塊Lanczos法、縮減法、Power Dynamics法、非對稱法和阻尼法，常用的是前4種方法。分塊Lanczos法具有收斂速度快等特點，常用在實體單元模型中。本例采用分塊Lanczos法進行求解。在對轉臺U型架精心模態分析時，因為求解的是U型架的固有頻率和振型，與所受外力沒有關系，所以模態分析時忽略外部載荷的作用。模態分析時施加的約束和網格劃分類型應與靜力分析時類似。

3.3 計算結果分析

經過計算分析，得到各階的固有頻率和振型云圖如圖5所示。

從圖5中可以看出，一階模態的固有頻率是319.42H z,U型架兩側都沿X軸正方向振動；二階模態的固有頻率是326.36H z,U型架左側沿X軸正方向振動，右側沿X軸負方向振動；三階模態的固有頻率是495.2H z,U型架左側沿Y軸負方向振動，右側沿Y軸正方向振動；四階模態的固有頻率是495.55H z,U型架兩側都沿Y軸正方向振動；五階模態的固有頻率是974.66H z,U型架兩側繞Y軸向右側發生彎曲；六階模態的固有頻率是999.33H z,U型架兩側繞Y軸向內發生彎曲。從分析結果可以得出，外框架前五階的固有頻率在319.42～999.33H z范圍。在機械系統的設計過程中，一般要求結構的固有頻率必須高于其最高工作頻率的5～8倍，考慮到有限元分析的固有頻率普遍偏高等因素，本文提出了高于機械系統工作頻帶的10倍要求，而兩軸速率轉臺工作時由外部激勵產生的工作頻率在10H z左右，遠小于外框架的第一階固有頻率319.42H z，所以轉臺工作時結構本身不會發生共振，設計是可以滿足要求的。

4 結論

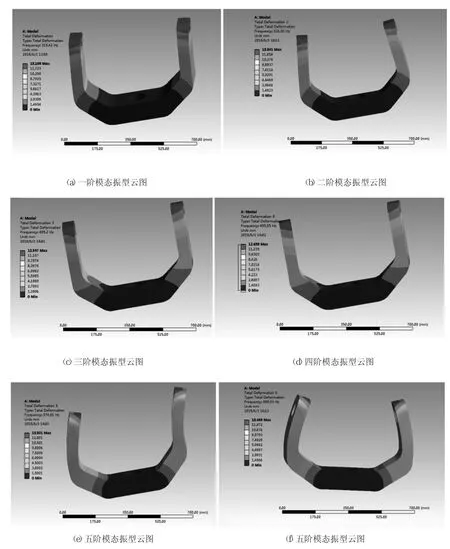
圖5 U型架模態振型云圖

通過ANSYS軟件對U型架靜態、模態分析可知，該U型架的設計滿足強度和剛度的要求，其動態特性良好，工作時不會發生共振。同時也發現，U型架的結構設計比較保守，可對U型架進行結構優化設計。ANSYS分析計算的結果為結構優化設計提供了重要的理論依據，可讓設計者避開結構的共振區間，避免共振的發生，提高機械系統設計的可靠性。