基于SEC模式的高考數學試題與新課程標準的一致性分析

林劍 張景信 廖光及

摘?要：借鑒SEC一致性分析模型，利用Nvivo質性分析軟件從內容主題維度和認知水平維度對2019年高考理科數學全國Ⅰ卷與《普通高中數學課程標準（2017年版）》進行編碼，通過矩陣運算分析數學高考試卷與課程標準一致性指標，結果發現全國Ⅰ卷與新課標顯著一致，但仍存在部分內容主題脫離新課標、靈活運用水平占比偏低等問題，建議進一步明確課標功能及創新考查方式，以培養學生數學核心素養.

關鍵詞：SEC模式;課程標準;高考數學

作者簡介：林劍（1995-），男，廣東肇慶人，碩士，助教，研究方向：數學與課程教學論;

張景信（1994-），男，山東臨沂人，碩士，中學二級教師，研究方向：數學與課程教學論;

廖光及（1988-），男，廣西南寧人，碩士，中學二級教師，研究方向：數學與課程教學論.

1?問題提出

《基礎教育課程改革綱要（試行）》[1]明確提出：“國家課程標準是教材編寫、教學、評價和考核的依據，是國家管理與評價課程的基礎.”高考在我國的基礎教育中占重要的地位，對中小學教育教學工作起著“風向標”與“指揮棒”的作用[2].只有當考試評價與課程標準相一致時，教學才會依課程標準要求而調整，課程改革的理念與目標才能得以貫徹及實現.我國教育部在2018年1月正式頒布《普通高中數學課程標準（2017年版）》（下稱“新課標”），并于當年秋季開學正式實施.因此，2019年理科高考數學全國卷是新課標實施后首次測驗的高考數學試題.高考評價內容與標準內容的匹配與否，命題是否體現了新課標的最新理念與要求均值得分析與探討.為此，本研究借鑒SEC模式，以量化研究的方法，探究數學高考試題與新課標是否存在適度一致性，以期為高考數學的命題工作提供借鑒與參考.

2?研究過程

目前，國際上在課程標準的一致性分析中，有三種較為認可的一致性分析模式：韋伯模式、SEC模式以及成功模式[3].由于三種分析模式均源于國外，而國外相較于國內在中小學階段學習內容及順序上存在諸般差異，基于模型可塑性與可移植性的考慮，本文采用SEC模式對數學高考試題與新課標間一致性進行分析.

2.1?研究工具

SEC（Survey?Of?Enacted?Curriculum）一致性分析范式是由美國威斯康星州麥迪遜大學的兩位學者安德魯·波特和約翰·史密森基于韋伯一致性分析工具建立的分析模式，其分析結果以定量形式呈現[3].模式以二維矩陣法計算一致性系數，即將課程標準與學業評價以內容主題維度和認知水平維度展開進行矩陣編碼，形成關于內容主題與認知水平的二維矩陣，根據公式計算波特一致性系數，以衡量課程標準與學業評價間匹配程度.波特一致性系數的定義為[4]：

P=1-∑Kk∑Jjajk-bjk2.

其中：?J，K分別表示二維矩陣的行數和列數，ajk，bjk為二維矩陣單元格的歸一化數值，P表示一致性指標.

由于波特一致性系數本質為課程標準與學業評價在不同認知水平下評價內容占比的矩陣運算，易受二維矩陣大小和高考試卷題型分值分布的影響，故不應以恒定的評價方案判斷高考試卷與課程內容標準是否一致.為了判斷高考試卷與課程內容標準的一致性是否在統計意義上顯著，美國學者Gavin?W?Fulmer（2011）建議通過仿真模擬形成一致性系數分布，取得0.05水平下的雙側臨界值，通過比較臨界值與一致性系數的大小，以判斷其在統計意義上的顯著性[5].

2.2?研究對象

本研究以2019年普通高等學校招生全國統一考試理科數學全國Ⅰ卷（下稱“全國Ⅰ卷”）與普通高中數學課程標準（2017年版）為研究對象，理科數學全國Ⅰ卷由教育部考試中心組織命題，適用于全國九個省（區），覆蓋范圍較廣，因此具有較強的代表性和權威性.通過對全國Ⅰ卷與新課標的一致性分析，可以了解當前數學高考試卷與新課標之間的一致性程度，為高考數學命題工作的改進提出依據.

為衡量數學高考試卷和新課標間的一致性，在深入分析數學高考試卷和新課標的基礎上，依據SEC模式構建“內容主題×認知水平”二維矩陣.在內容主題上，新課標分為必修課程、選擇性必修課程和選修課程，以函數、幾何與代數、概率與統計、數學建模活動與數學探究活動為主線貫穿其中，其中必修課程和選擇性必修課程均為數學高考試題命題范圍，結合新課標中課程主題單元分類，將內容主題劃分為：S1集合;S2復數;S3常用邏輯用語;S4相等關系與不等關系;S5數列;S6三角函數;S7冪函數、指數函數、對數函數;S8函數及導數;S9幾何與向量;S10解析幾何;S11計數原理;S12概率;S13統計.在認知水平上，新課標中并未對認知水平進行層級劃分，結合《義務教育數學課程標準（2011版）》對相關行為動詞基本含義的描述以及考試大綱對知識要求層次的劃分，將認知水平劃分為：了解、理解、掌握以及靈活應用[6].

2.3?編碼結果

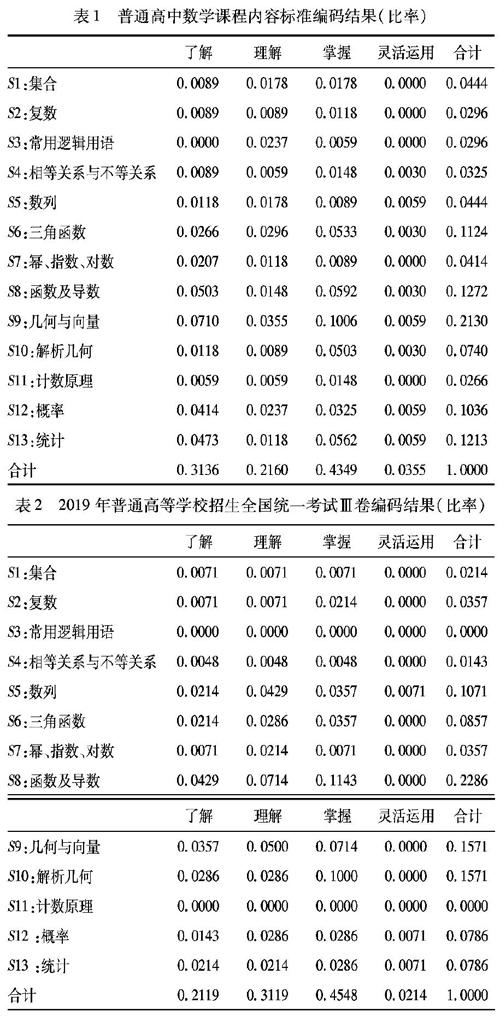
依據內容主題的確定及認知水平的劃分，構建了用于數學高考試卷和新課標編碼的13×4二維矩陣表格，分別對應13個內容主題和4個認知水平分類.

2.3.1?《課程標準》的編碼

對新課標各主題內容要求進行編碼的工作量較大，但不同內容要求間以相關行為動詞進行明顯區分，故引入Nvivo質性分析軟件對課程標準開展編碼工作，以減少人工編碼所造成的耗時與誤差.在課題組的系列文章中[7][8]，通過對Nvivo軟件的編碼結果與人工編碼結果進行相關性分析，已驗證了Nvivo軟件編碼的有效性，故直接運用Nvivo軟件對新課標進行編碼.通過Nvivo軟件的關鍵詞編碼功能創建節點，在內容主題維度以主要內容類目為關鍵詞建立自由節點，在認知水平維度以相關行為動詞為關鍵詞建立自由節點，進而以矩陣節點分析方式形成新課標關于內容主題與認知水平的二維矩陣.

2.3.2?數學高考試卷的編碼

對數學高考試卷以人工編碼的方式進行編碼，依據試題內容與新課標內容主題單元的對應關系確定知識主題，根據試題考核意圖和所使用的行為動詞確定認知水平要求，將每道試題以其考點參考答案所設定的分值為計量單位，賦值于?“內容主題×認知水平”二維矩陣中相應的單元格.在對數學高考試卷編碼的過程中，應遵循以下幾點：其一，數學試題的考查多為若干個知識點間的綜合考查，故應對解題過程中涉及的所有知識點進行賦值;其二，數學高考試卷存在兩個選做題，分別是坐標系與參數方程和不等式選講，但在新課標的高考命題范圍中并未涉及這兩個內容模塊，為避免對一致性系數的影響，故以必做題得分140分為卷面總分.

3?結論與分析

3.1?Porter一致性指標分析

調用Porter一致性計算公式對歸一化的二維矩陣進行矩陣運算，得到高考試卷與課程內容標準的一致性指標為0.6104.為衡量一致性系數在統計意義上是否具有顯著性，在Matlab軟件中調用unidrnd函數，將課程標準的338個內容要求及高考試卷140分的分值分別隨機賦值于兩個13×4的二維矩陣中，通過累次仿真模擬產生一致性系數分布.根據中心極限定理，P近似服從于正態分布，在顯著水平α=0.05下進行雙側檢驗，高考試卷與課程內容標準之間一致性系數為0.6104，即P∈0.6072，0.7422，經假設檢驗一致性系數在統計意義上顯著.

3.2?圖表分析

3.2.1?總體一致性分析

由圖1可知，全國Ⅰ卷在劃定的13個內容主題及其不同的認知水平上均與新課標存在偏離，但偏離范圍僅在-0.03到0.04間，偏離幅度較小.全國Ⅰ卷在集合、復數、相等關系與不等關系、數列、三角函數、初等函數、概率與統計內容主題的考查與課程內容標準的要求基本一致，偏離幅度小于0.020;對函數與導數、幾何與向量、解析幾何的考查略高于課程內容標準，其中對函數與導數在理解和掌握維度的考查最重，偏離課程內容標準達0.039;對常用邏輯用語、計數原理的考查低于課程內容標準的要求，與課程標準的最大偏離幅度分別為-0.031，-0.021.盡管全國Ⅰ卷與新課標在各內容主題上均存在偏離，但由于各考查部分的偏離程度不大，故全國Ⅰ卷與新課標的Porter一致性系數在統計意義上仍達顯著水平.

3.2.2?內容主題維度一致性分析

如圖2反映，在內容主題維度上，全國Ⅰ卷的考查與新課標內容標準的要求存在偏離，是導致一致性偏低的重要原因.全國Ⅰ卷與新課標的差異主要體現在對數列、函數與導數、解析幾何等內容主題上的考查，而在集合、復數等內容主題上的差異較小，原因在于我國現行關于課程標準的定位是國家面向全體學生提出的最低限度的學習要求，而作為以選拔人才為目的的高考，不應拘泥于課程標準提出的統一要求，因此在難度較高內容主題中適當增加命題比例符合高考的基本定位.此外，新課標以概率與統計作為高中數學課程的四大主線之一，特別強調了概率與統計對學生數據分析核心素養的培養，因此2019年全國Ⅰ卷增加了概率與統計內容主題的分值和難度，一定程度上提高了學生對該內容主題的關注，符合新課標發展數學核心素養的要求.此外，新課標對常用邏輯用語及計數原理同樣存在要求，而全國Ⅰ卷并未對該部分內容進行考查.

3.2.3?認知水平維度

觀察圖3可知，全國Ⅰ卷的考查與新課標內容標準的要求在各認知水平維度上的比重差異較小，反映了全國Ⅰ卷與新課標在認知水平維度上適度一致.新課標在認知水平上的分布比重為“掌握”>“了解”>“理解”>“靈活運用”，明顯區別于全國Ⅰ卷“掌握”>“理解”>“了解”>“靈活運用”的認知水平要求，基于新課標文本分析發現，內容標準中存在多處由“了解”到“掌握”認知水平的跨越，而“了解”“理解”“掌握”是學生認知發展遞進的過程，因此高考試卷的認知水平比例更為符合學生的認知發展規律.此外，2019年全國Ⅰ卷引入了“維納斯身高”“新藥臨床試驗”等具有現實意義背景的試題，以考查學生的靈活運用水平，而無論課程標準抑或高考試卷在靈活運用水平的比重仍不足5%，宜加大新課標與高考試卷對于該水平的要求和考查，以培養學生數學核心素養.

4?啟示與展望

4.1?明確課標功能，追求適度一致

我國現行關于課程標準的定位是國家面向全體學生提出的最低限度的學習要求，允許學有余力的學生超出這一目標.即課程標準是一個彈性框架，高考應該在框架中自由命題，不應拘泥亦不能脫離課程標準.但新課標并未對坐標系與參數方程、不等式選講存在要求，而在2019年全國Ⅰ卷中卻仍依照舊課程內容標準要求進行命題;此外，新課標對常用邏輯用語及計數原理存在要求，而全國Ⅰ卷并未對該部分內容進行考查.課程標準與考試評價脫節，將會打破課標、教學、評價三者間平衡關系，而課程改革的理念與目標亦將無法得到落實.由此建議高考試卷命題人應明確課程標準的功能，結合內容主題的比重合理調整高考試卷的考查范圍及分值，追求其與課程內容標準要求的適度一致.

4.2?創新考查方式，培養核心素養

美國國家數學咨詢委員會特別強調高水平的認知能力對提高國家競爭力、國民素養及生活水平的重要性[9].課程標準知識要求層次中的“了解”與“理解”層次屬于低級認知水平，“掌握”和“靈活運用”層次屬于高級認知水平[9].相比舊課標，無論新課標抑或2019年全國Ⅰ卷均提高了在高級認知水平中的比重，由2018年的36%增加至43%，增幅達19.4%.雖在靈活運用水平的比重仍不足5%，但在新課標中增設了教學案例與評價案例，且在高考試卷中創新性地引入了具有現實背景的試題，為數學思維的訓練及核心素養的培養創設先河.建議教師依據新課標的要求，在教學中進一步提高掌握和靈活運用水平的要求，并在高考試卷中加大考查比例，引導高級認知水平在課堂中滲透.

參考文獻：

[1]鐘啟泉.基礎教育課程改革綱要（試行）解讀[M].?上海：華東師范大學出版社，2001.

[2]昌慶鐘.歷史高考與課程標準的“適度一致性”分析——基于2012～2014年文綜（歷史）新課標全國卷的研究[J].教育學術月刊，2015（03）：102-108.

[3]羅瑩，郭晨躍，李勇.高考物理命題的一致性研究及其對物理教育的啟示[J].課程·教材·教法，?2012，?32（11）：?105-111.

[4]Porter?A?C.?Measuring?the?Content?of?Instruction：?Uses?in?Research?and?Practice[J].?Educational?Researcher，?2002，31（07）：3-14.

[5]Fulmer?G?W.?Estimating?Critical?Values?for?Strength?of?Alignment?Among?Curriculum，?Assessments，and?instruction[J].?Journal?of?Educational?and?Behavioral?Statistics，2011，36（06）：381-402.

[6]中華人民共和國教育部.?義務教育數學課程標準[M].?北京：?北京師范大學出版社，?2011.

[7]林劍，周瑩，路夢綺.不同版本教師用書與課程標準一致性分析——以蘇教版、北師版高中數學必修（教師用書）為例[J].教學與管理，2019（12）：74-77.

[8]林劍，路夢綺，周瑩.基于NVIVO編碼的課程標準一致性分析——以2018年高考數學全國卷Ⅲ為例[J].考試研究，2018（05）：18-23.

[9]周瑩，廖麗紅，梁鑫，黃懷芳.初中數學教材與課程標準的一致性研究——以“人教版”和“湘教版”中的函數習題為例[J].數學通報，2017，56（05）：6-9+14.

（收稿日期：2019-09-03）