基于無矩理論的凹版印刷機運動薄膜橫向振動特性及穩定性

武吉梅 邵明月 田 振 雷文姣 王 硯

1．西安理工大學機械與精密儀器工程學院，西安, 710048 2．西安理工大學印刷包裝與數字媒體學院，西安, 710048 3．西安理工大學土木建筑工程學院，西安, 710048

0 引言

印刷過程中，中間印刷滾筒對薄膜的約束可視為薄膜的中間支承，不同的支撐位置對薄膜的振動特性有影響,因此，研究具有中間剛性支承運動印刷薄膜的振動問題，對控制印刷過程中薄膜的振動及提高印品的套印精度具有重要的意義。

近年來，軸向運動系統的橫向振動和穩定性問題的研究已經取得較大成果，但對具有中間支承的薄膜的振動和穩定性的研究很少。TANG等[1-3]分別對軸向運動的弦線、黏彈性梁、薄板的橫向振動問題進行了研究。MA等[4]采用有限差分法離散動力學方程，研究了變密度運動薄膜的振動控制問題。WANG等[5]運用薄板理論和二維黏彈性本構關系，研究了軸向運動的壓電黏彈性板的動力學特性和穩定性。SHINA等[6]應用哈密頓原理建立了無滑動邊界條件下運動薄膜的微分方程，研究了軸向運動薄膜的面內和面外的動力學特性。吳曉[7]采用解析法研究了無軸向運動速度且具有中間支承的薄膜的橫向振動特性。MARYNOWSKI[8]采用二維流變理論，建立了軸向運動的黏彈性薄膜材料的動力學模型。劉金堂等[9]采用微分求積法，研究了受面內載荷作用的軸向運動薄板的橫向振動問題。趙鳳群等[10]對四邊固支矩形運動薄膜的非線性振動特性進行了分析。NGUYEN等[11-12]研究了具有軸向運動速度的薄膜的橫向振動特性和控制問題。WU等[13-14]運用振動理論和達朗貝爾原理，分別研究了多輥支承的軸向運動紙帶和彈性邊界下運動薄膜的振動特性。

本文通過研究，將單剛性支承薄膜拓展到若干剛性支承情況下薄膜的橫向振動特性及穩定性問題，分析具有剛性支承時系統的固有振動頻率與張力、速度之間的關系曲線，給出薄膜穩定工作的臨界速度及工作范圍。

1 振動模型的建立

圖1為具有中間支承印刷薄膜的工作示意圖。對于機組式凹版印刷機，I1、I2、I3為壓印滾筒，P1、P2、P3為印版滾筒。高速運動的薄膜從幾組滾筒之間的接觸表面通過，完成多色套印印刷。印刷過程中，運動的薄膜類承印物遵循薄膜振動理論，將中間印刷滾筒對薄膜的作用作為薄膜的中間支承處理，并用線分布的約束反力代替，將印刷機第一色組和最后色組的印刷滾筒對薄膜的作用作為邊界條件處理，建立薄膜的動力學模型。

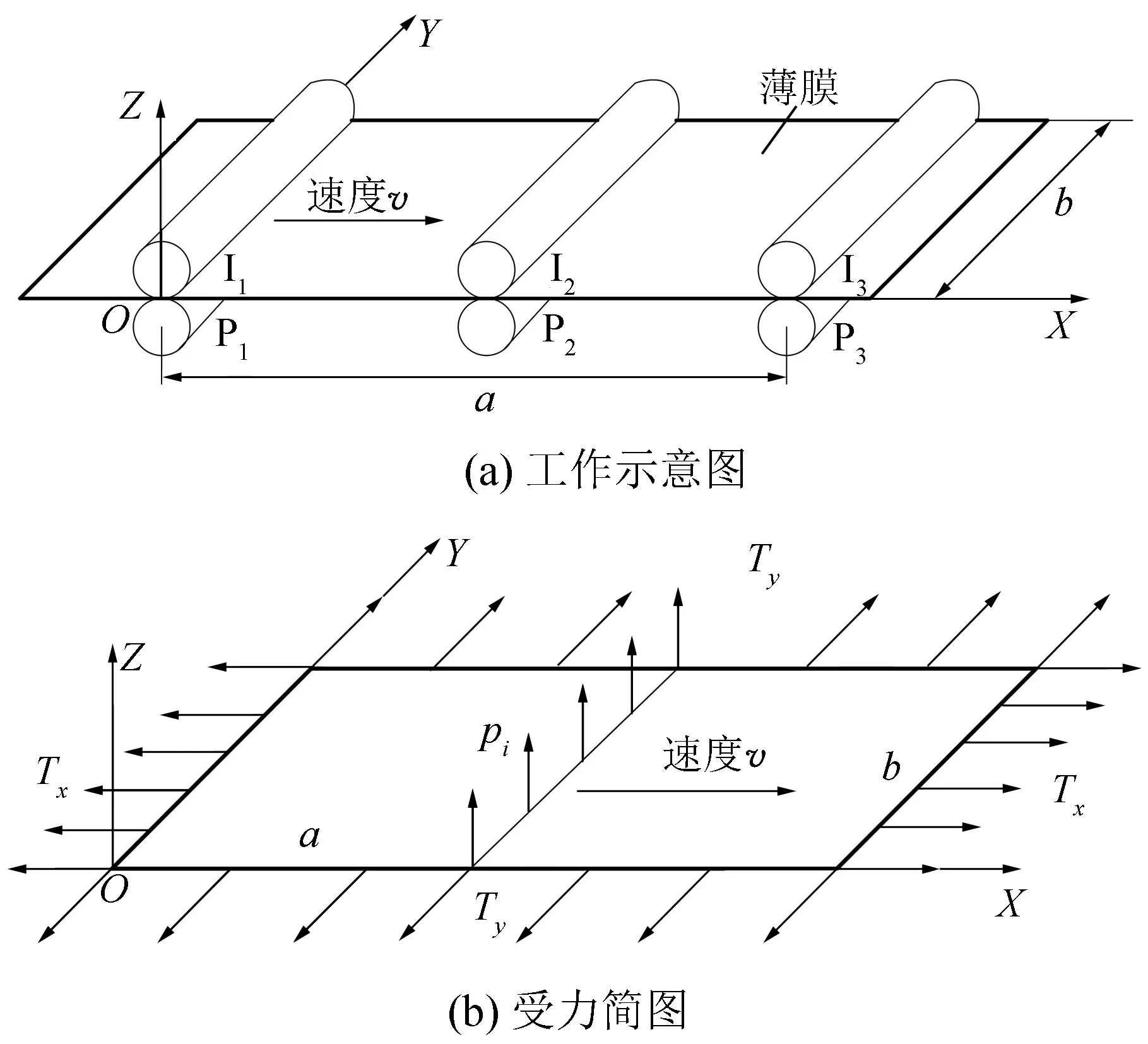
圖1 印刷薄膜工作簡圖和受力簡圖Fig.1 Schematic diagram of an axially moving membrane

如圖1所示，選取OXYZ坐標系：以薄膜的運動方向為X方向，該方向的運動速度為v；薄膜的寬度方向為Y方向；橫向振動的位移方向為Z方向。a、b分別為兩組印刷滾筒間薄膜的長度和寬度；ρ為單位面積薄膜的質量；Tx為薄膜在X方向上受到單位長度的拉力，N/m；Ty為薄膜在Y方向上受到單位長度的拉力，N/m。

基于無矩理論[15]和D’Alembert原理得出軸向運動印刷薄膜橫向振動偏微分方程：

q(x,y,t)

(1)

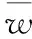
四邊固支薄膜的邊界條件為

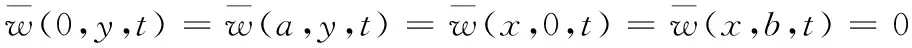
(2)

2 特征方程的求解

設式(1)的解為

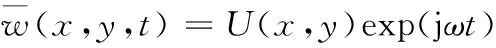
(3)

式中，U(x)是振型函數；ω為運動薄膜的振動頻率。

具有中間支承的印刷薄膜固有振動時，中間支承的約束反力隨時間的變化規律與印刷薄膜的振動規律相同。式(1)的分布載荷q(x,y,t)為薄膜沿Z方向所受均布外力，可表示為

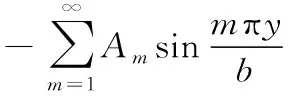
(4)

(5)

式中，N為中間支承的個數；xi為第i個支承到Y軸距離；pi為第i個支承對薄膜的支承反力；δ(x-xi)為Dirac-delta函數，表示作用在(xi,y)位置上的支承反力。

設振型函數為

(6)

由四邊固支的邊界條件有

fm(0)=fm(a)=0m=1,2,…

(7)

將式(3)、式(4)、式(6)代入式(1)并整理得

(8)

(9)

對式(8)進行Laplace變換得

(10)

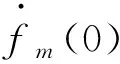
對式(10)進行Laplace逆變換，并代入式(7)可得

sin(λ(x-xi))g(x-xi)

(11)

將式(11)代入式(6)，然后再代入式(3)，得到具有中間支承四邊固支運動印刷薄膜的固有振動動力響應：

(12)

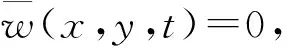
(13)

(14)

i,j=1,2,…,N

當薄膜中間支承為彈性支承時，pj=-kjfm(xj),其中，kj為第j個彈性支承的剛度系數。由式(11)得到具有中間支承的運動薄膜的振動頻率特征方程：

(15)

3 數值計算分析

本文以陜西北人FR-300無軸傳動高速機組式凹版印刷機的承印物薄膜為實例，計算分析具有中間剛性支承的運動印刷薄膜的橫向振動特性及穩定性。該印刷機的基本參數如下：薄膜幅寬b=1.05 m，薄膜長度a=3 m，薄膜速度v=5 m/s，薄膜張力Tx=90 N/m，Ty=10 N/m，密度ρ=0.07 kg/m2。

3.1 具有一個中間剛性支承

圖2所示為一個中間剛性支承的印刷薄膜，中間支承的位置與左端的距離為a/h，由式(13)可得中間具有一個剛性支承運動印刷薄膜的振動頻率特征方程：

(16)

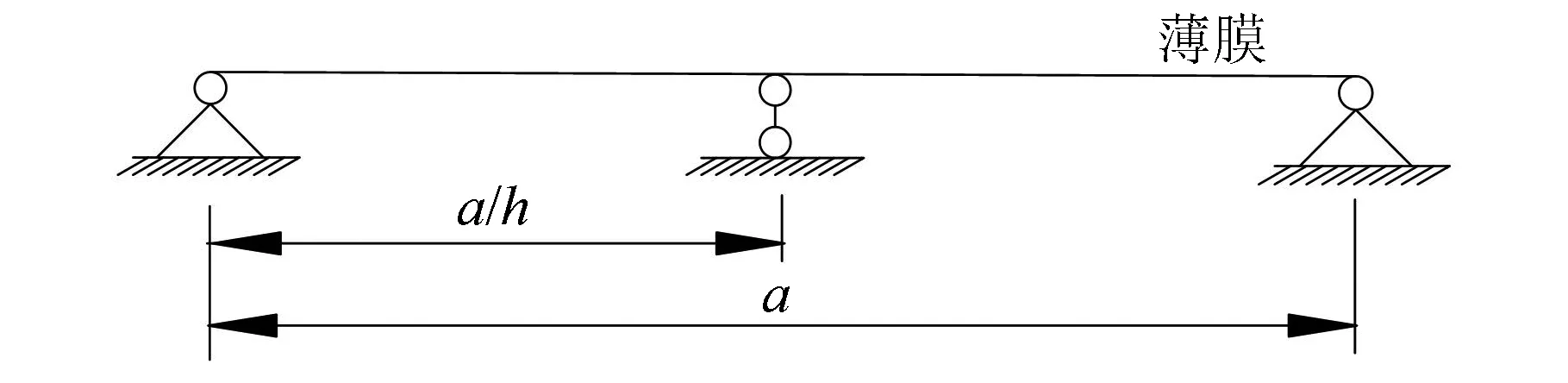
圖2 中間一個剛性支承Fig.2 Single intermediate rigid support

由式(16)可得

(17)

由文獻[7]可知，沒有中間支承時的四邊固支薄膜橫向振動頻率特征方程為

sin(λa)=0

(18)

h=2時，式(17)化為

(19)

具有一個剛性支承運動薄膜的中間支撐位置為x=1.5 m，則運動薄膜的振動圓頻率為

(20)

v=0時，無軸向速度薄膜的振動圓頻率為

(21)

v=0時的振動圓頻率表達式與文獻[7]中的中間一個剛性支承的薄膜振動圓頻率表達式一致，由此說明本文所用方法的正確性。

由式(20)、式(21)可求出v=5 m/s及v=0時的運動薄膜振動圓頻率，分別用ωv=5和ωv=0表示，如表1所示。

表1 具有一個中間剛性支承薄膜的振動圓頻率

由表1可知，v=5 m/s及v=0時的薄膜振動圓頻率不同，因此，軸向運動速度對印刷薄膜橫向振動影響顯著。由式(20)可得印刷薄膜固有振動圓頻率ω與軸向運動速度v之間的關系曲線，如圖3所示。

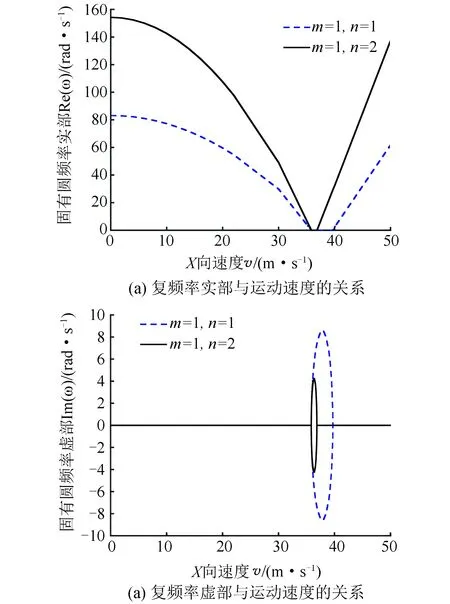
圖3 薄膜振動復頻率與軸向運動速度的關系Fig.3 Relationship between complex frequency and axial moving speed

由圖3可以看出，速度0～35.86 m/s內，薄膜復頻率ω11逐漸降低至0；在速度范圍35.86～39.72 m/s內，Re(ω)=0，此時Im(ω)出現，印刷薄膜系統發散失穩。當v>39.72 m/s時，印刷薄膜系統恢復穩定。對于薄膜復頻率ω12，速度在35.86～36.86 m/s內時，Re(ω)=0，印刷薄膜系統發散失穩；當v>36.86 m/s時，印刷薄膜系統恢復穩定。

圖4所示為單剛性支撐薄膜軸向速度v=5 m/s時ω與Tx的關系。由圖4可知，隨著Tx的增大，ω逐漸增大。當v=5 m/s時，在0≤Tx<1.75 N/m內，Re(ω)=0，虛部突然增大，印刷薄膜系統處于發散失穩狀態；當Tx>1.75 N/m時，虛部為零，印刷薄膜系統恢復穩定。

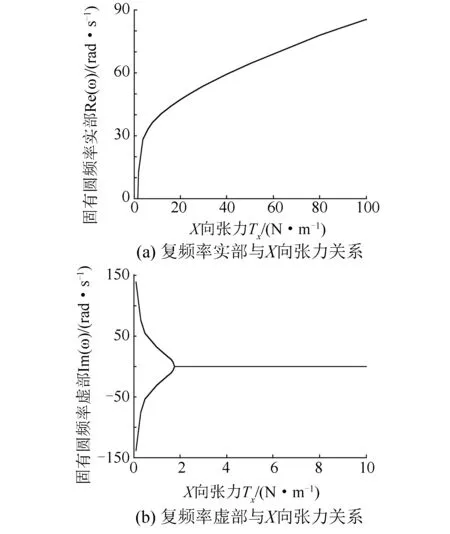
圖4 薄膜復頻率與X向張力關系(v=5 m/s)Fig.4 Relationship between the complex frequency and tension(v=5 m/s)

3.2 中間具有兩個剛性支承

圖5為中間具有兩個剛性支承的運動印刷薄膜示意圖。最左端與第一個剛性支承位置的距離x1=a/3，即x1=1 m。最左端與第二個剛性支承位置的距離x2=2a/3，即x2=2 m。

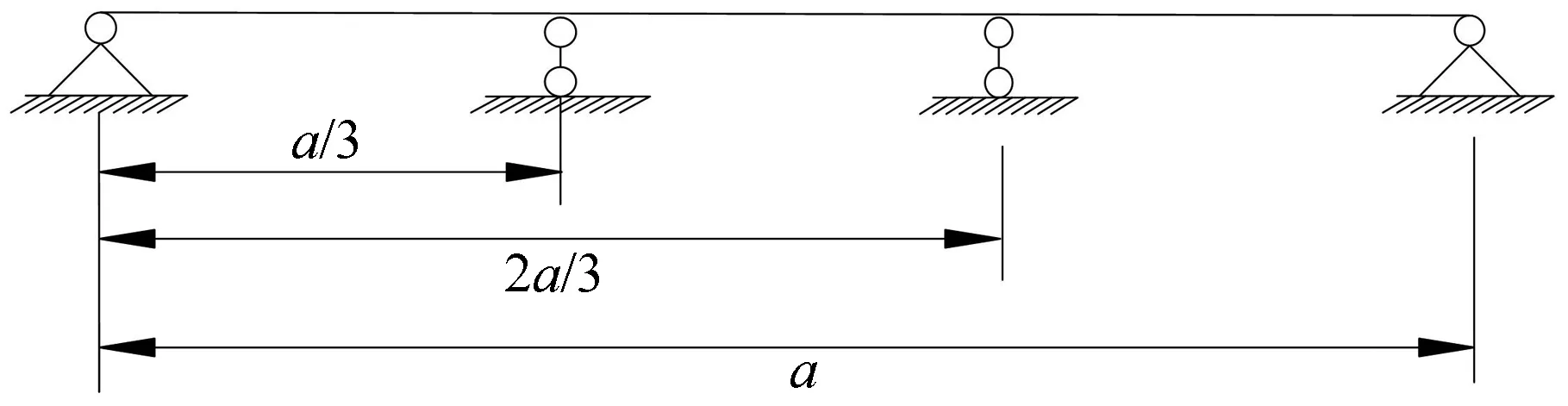
圖5 中間具有兩個剛性支承的運動印刷薄膜Fig.5 Moving membrane with two intermediate rigid supports

由式(13)可求得中間具有兩個剛性支承運動印刷薄膜振動頻率特征方程：

A11A22-A21A12=0

(22)

具有2個中間剛性支承印刷薄膜可以看成三段長度均為a/3且無中間支承運動印刷薄膜。則其中一段印刷薄膜固有振動頻率特征方程為

(23)

那么具有兩個中間剛性支撐運動印刷薄膜的振動圓頻率為

v=0時，式(24)退化為無軸向速度且具有兩個中間剛性支承的運動印刷薄膜的振動圓頻率：

(25)

退化后的振動圓頻率表達式與文獻[7]中的中間兩個剛性支承的薄膜固有振動圓頻率表達式一致，由此說明本文所用方法的正確性。

由以上分析可類推出具有N個均勻分布剛性支承運動印刷薄膜固有振動圓頻率：

(26)

v=0時，式(26)退化為無軸向速度的具有N個均勻分布剛性支承薄膜的振動圓頻率：

(27)

由式(24)可求得具有兩個中間剛性支承運動印刷薄膜的振動圓頻率ω與軸向運動速度v之間的關系，如圖6所示。

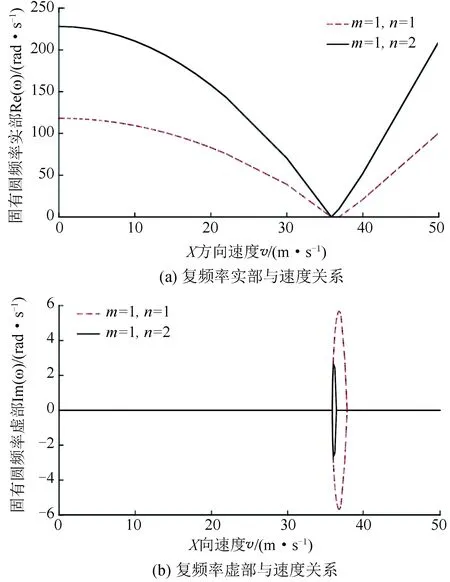
圖6 兩個剛性支承薄膜復頻率與速度的關系Fig.6 Relationship between complex frequency and moving speed of membrane with two rigid supports

由圖6可以看出，對于具有兩個中間剛性支承運動印刷薄膜復頻率ω11，速度在0～35.86 m/s內時，頻率逐漸減小至0，在35.86～37.62 m/s內時，Re(ω)=0，Im(ω)出現，印刷薄膜系統處于發散失穩狀態。當v>37.62 m/s時，印刷薄膜系統恢復穩定狀態。對于印刷薄膜復頻率ω12，速度在35.86～36.31 m/s內時，Re(ω)=0，印刷薄膜系統處于發散失穩狀態；當v>36.31 m/s時，印刷薄膜系統恢復穩定狀態。

圖7所示為具有兩個中間剛性支承印刷運動薄膜Y方向張力Ty分別為10 N/m和20 N/m時，薄膜的復頻率ω與張力Tx之間的關系曲線。由圖7可知，X向張力Tx為定值時，Y向張力越大，印刷薄膜的振動頻率越大。當Ty為定值時，隨著Tx增大，印刷薄膜振動頻率實部增大。當Tx>5 N/m時，印刷薄膜振動頻率實部與Tx為線性關系。01.75 N/m，虛部為零，印刷薄膜系統恢復穩定。

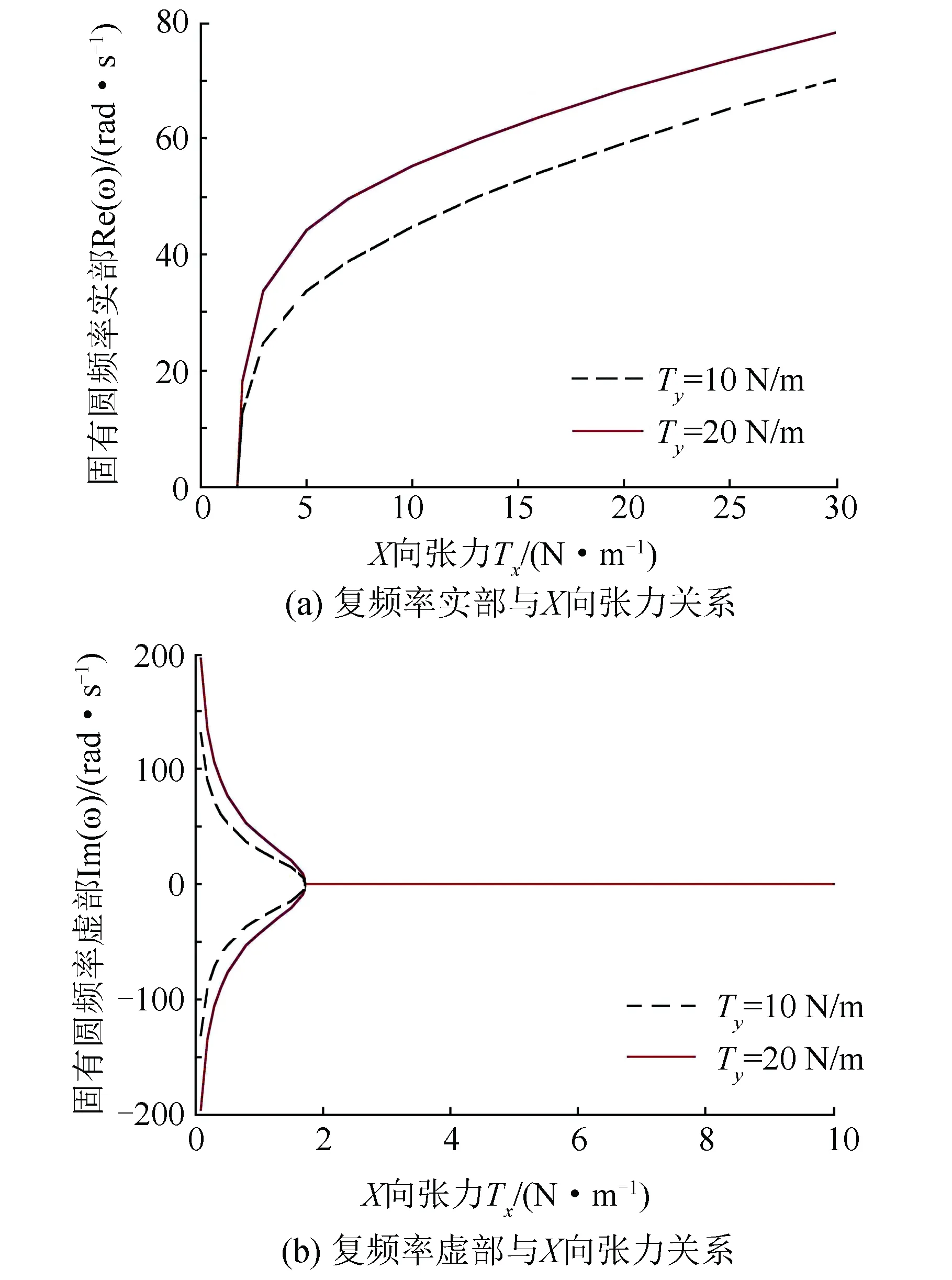
圖7 兩個剛性支承薄膜復頻率與張力Tx的關系Fig.7 Relationship between complex frequency and tension with two rigid supports

對于具有兩個中間剛性支承的運動印刷薄膜，剛性支承的位置x1、x2會對印刷薄膜的振動頻率有影響。令x1=a/10，分別求v=5 m/s及v=0時薄膜的振動頻率與支承位置x2二次插值擬合的關系，如圖8所示。

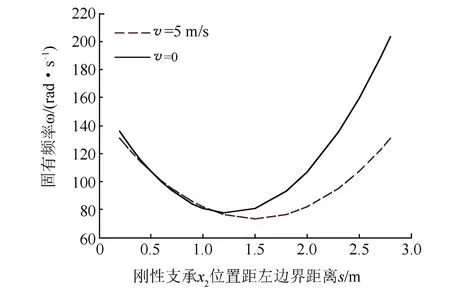
圖8 薄膜的振動頻率與支承位置的關系Fig.8 Relationship between transverse vibration natural frequency of membrane and supporting position

由圖8可以看出，v=0情況下，x2在0～1.2 m范圍內時，圓頻率ω隨x2的增大而減小；x2>1.2 m時，圓頻率隨x2的增大而增大。v=5 m/s情況下，01.5 m時圓頻率隨x2的增大而增大。相比于v=0情況下，v=5 m/s時圓頻率增大的趨勢明顯減小，由此可知印刷薄膜軸向運動速度越大時，支承位置的變化對印刷薄膜的振動頻率影響越不明顯。

4 結論

(1)運動速度v=0時，退化結果與文獻[5]結果相一致，證明本文的計算方法是正確的；對理論分析結果進行實例計算。

(2)對于中間單剛性支承印刷運動薄膜，通過對其振動頻率與運動速度、張力之間的關系的分析，獲得了中間單剛性支承薄膜振動發散失穩的臨界速度為35.855 m/s。軸向速度v=5 m/s時，張力范圍為0～1.75 N/m時， 薄膜處于發散失穩狀態；當Tx>1.75 N/m時, 系統又恢復穩定。

(3)對于具有中間兩剛性支承的印刷運動薄膜，不同的剛性支承位置對薄膜的振動頻率產生影響。v=0情況下，第二個剛性支承位置x2在0～1.2 m內時薄膜的振動頻率隨x2的增大而減小；x2>1.2 m時振動頻率又呈增大趨勢。v=5 m/s情況下，x2≤1.5 m時振動頻率隨x2的增大而減小；x2>1.5 m時振動頻率呈現增大的趨勢。薄膜軸向運動速度越低，支撐位置的變化對薄膜振動頻率影響越明顯。