新型無油渦旋壓縮機性能

彭 斌 趙生顯 李要紅

蘭州理工大學機電工程學院，蘭州，730050

0 引言

渦旋壓縮機是繼離心式壓縮機、往復式壓縮機、螺桿式壓縮機之后出現的第4代容積式壓縮機，無油渦旋壓縮機采用新的散熱形式，用托盤來隔絕壓縮機工作腔和曲軸傳動系統，使得曲軸傳動系統可以采用脂潤滑而不會影響工作腔的無油狀態，通過成對的角接觸球軸承來平衡氣體力，它又稱為新型容積式壓縮機。隨著全球氣候問題的日益嚴重和不可再生資源的短缺，節能、減排、新能源的開發利用已成為當今世界各國研究的重要課題之一。 “十三五”發展規劃將綠色發展作為一種全新的發展理念，同時加大實施新能源汽車推廣計劃，提高電動車產業化水平，作為新能源汽車氣源動力的無油壓縮機也必將得到迅猛發展[1]。新能源汽車無油壓縮機要求質量小、體積小、高比功率，而且能在不同的工況下保持高效、穩定的工作狀態。

為了獲得高效的運轉效率和可靠性，一般都在壓縮機腔體中噴入潤滑油，噴入的潤滑油可以在渦旋齒和渦旋盤底面形成一定厚度的油膜，形成的油膜可以起到密封渦旋壓縮機軸向和徑向間隙的作用，同時，噴入的潤滑油還能帶走壓縮腔內的熱量，降低渦旋壓縮機的溫度。渦旋壓縮機作為制冷壓縮機和有油潤滑空氣壓縮機，技術已趨近成熟，產品已能穩定運行，但在食品、醫藥、紡織和新能源汽車等領域，壓縮空氣是絕對不能含油的。目前有兩種方法來獲得無油壓縮空氣：1采用高性能過濾器，盡可能實現無油，但增加油氣分離器會導致系統龐大，同時壓縮氣體中含有的潤滑油凝結在壓縮系統中的其他設備上，會影響其正常工作；2采用無油渦旋壓縮機，由于無油渦旋壓縮機自身的優良結構特性，它在新能源汽車應用上具有其他壓縮機無法比擬的優勢。

在無油渦旋壓縮機領域，有很多學者也進行了相關的研究工作。LAI等[1]設計并測試了用于電動汽車的一種無油渦旋壓縮機，指出軸向和徑向間隙對無油渦旋壓縮機的性能影響非常大[2]；ZHAO等[3]對用于燃料電池汽車的噴水無油渦旋壓縮機進行了詳細的性能研究；房師毅等[4]在未考慮介質與渦旋齒換熱的情況下，計算了新型無油渦旋壓縮機熱力學過程；WANG等[5]設計開發了用于航空航天領域的制冷無油渦旋壓縮機，建立了熱力學模型，并對樣機的性能進行了研究；YANAGISAWA等[6]對無油渦旋壓縮機的容積效率和總效率進行了詳細研究； SHAFFER等[7]分別設計了一種塑料和金屬材質的新型無油渦旋壓縮機，并對其兩者的性能進行了對比研究，相對金屬材質，塑料材質對溫度更加敏感，但加工精度要求低，同時成本也相對較低；李超等[8]從運動學和機構學的角度對小曲拐進行受力分析，得到了3個小曲拐在不同曲軸轉角下的變形和應力狀態。王俊亭[9]對風冷無油渦旋壓縮機的熱力學及渦旋盤的變形進行了詳細分析。

目前無油渦旋壓縮機采用噴水潤滑或通過保證渦旋齒精度、渦旋齒間的間隙和改進散熱系統來獲得高性能[10-11]。由于采用噴水潤滑需要相應的水循環，一般在工業應用中采用較少；而通過提升渦旋齒精度、保證渦旋齒間的間隙和改進散熱系統就成為目前工業中普遍采用的手段。針對目前無油渦旋壓縮機的研究現狀、工作特點和存在的不足，研制開發了一種新型無油渦旋壓縮機并對其熱力學模型和試驗進行了詳細研究。依據新型無油渦旋壓縮機的幾何模型，基于熱力學第一定律、質量守恒定律和氣體狀態方程，綜合考慮工作腔的兩種內泄漏以及吸氣加熱模型，構建了整機的熱力學模型。通過試驗定量化研究了無油渦旋壓縮機的性能特性。

1 幾何模型

1.1 無油渦旋壓縮機的基本原理

本文研制開發的新型無油渦旋壓縮機樣機結構見圖1。靜盤和動盤均為單渦旋齒結構，相位角相差180°安裝，且其背部分布有散熱片。靜盤的背面設有一個端板，與靜盤的散熱片構成了一個氣流通道，在動盤的背面設有一個托盤，與動盤的散熱片形成了一個氣流通道。渦旋齒的齒頂加裝自潤滑式摩擦副，托盤上安裝有小曲拐，目的是防止動盤的自轉。小曲拐上分別帶有自潤滑的密封軸承，靜盤通過螺栓固定在支架體上，動盤在靜盤和支架之間平動。動盤中心連接主軸，動盤在主軸的帶動下旋轉，主軸上裝有帶風罩的冷卻風輪，風罩與風輪形成氣流通道。皮帶輪帶動冷卻風輪旋轉，將樣機內部產生的熱量排出到外界。

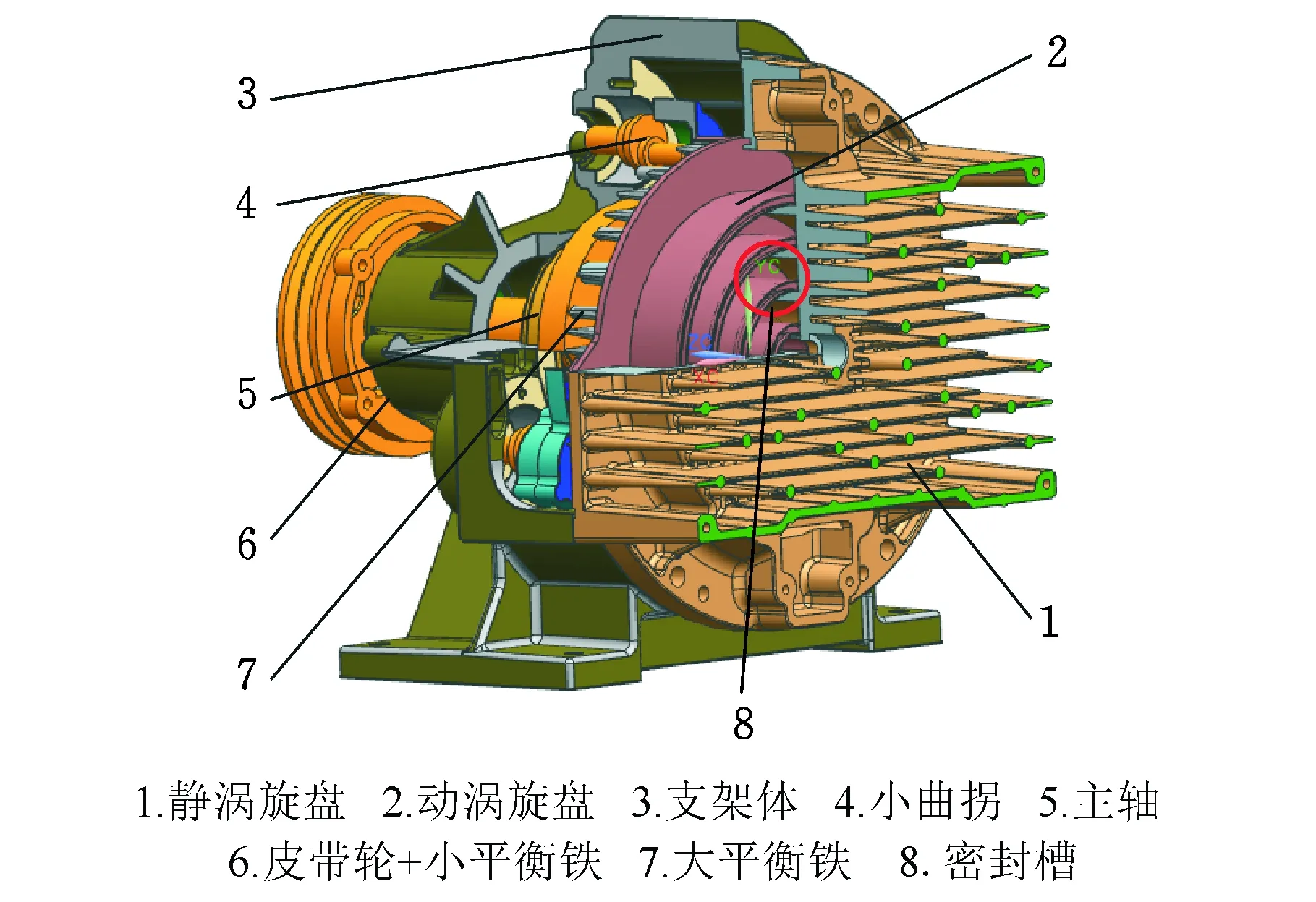
圖1 無油渦旋壓縮機Fig.1 Oil-free scroll compressor

1.2 型線基本方程及幾何參數

采用圓漸開線推導出渦旋盤的型線方程，則圓漸開線基準線方程：

(1)

式中，rb為基圓半徑；φ為漸開線的展角。

基線確定后，根據法向等距曲線的特點[6]，確定渦旋盤的內外側型線方程。內圈圓漸開線方程為

(2)

式中，α為漸開線的發生角。

外圈圓漸開線方程為

(3)

根據上述渦旋型線方程，結合表1中所列出的幾何參數， 運用基線法生成等截面渦旋內外圈的型線見圖2。

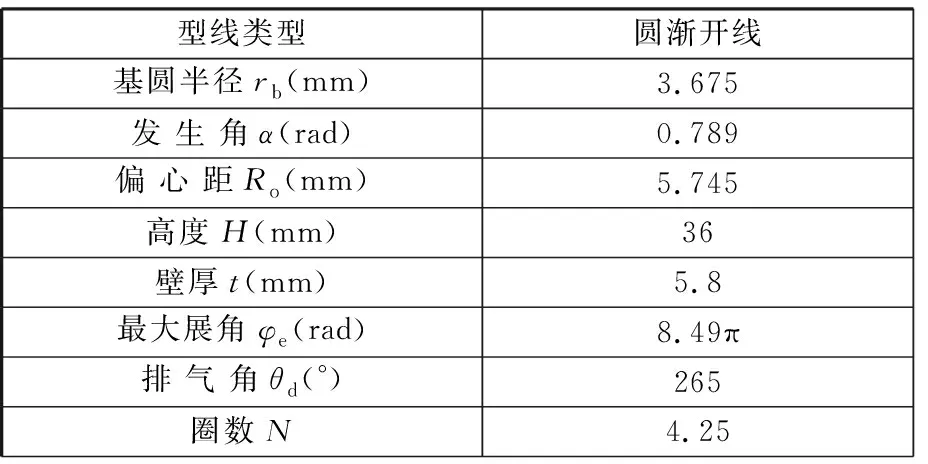
表1 渦旋壓縮機的幾何參數

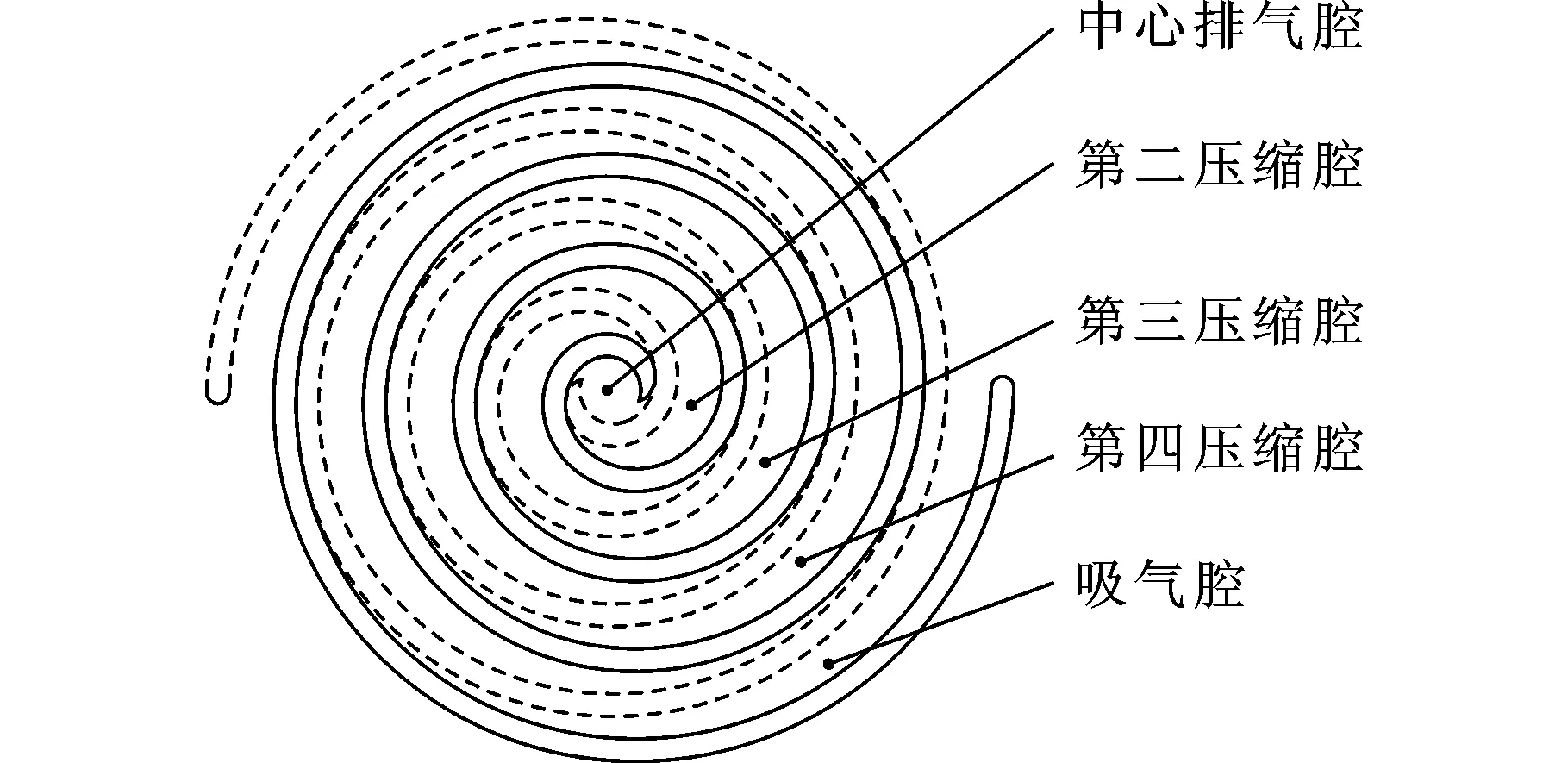
圖2 無油渦旋壓縮機型線Fig.2 Oil-free scroll compressor profile

1.3 工作腔容積變化分析

工作腔容積的變化依據單一腔體從吸氣開始到排氣結束的容積來計算[12]。

(1)吸氣腔容積。當主軸轉角θ∈(0,2π)時，渦旋壓縮機處于吸氣狀態，吸氣腔打開，動渦盤隨著偏心主軸的轉動將氣體吸入吸氣腔。吸氣腔容積

Vs=rbRoH[θ(2φe-θ-π)-2(φe-π+α)·

(4)

(2)壓縮腔容積。以圓漸開線作為基線所形成的渦旋齒，則腔體內部的容積

(5)

式中，i為壓縮腔個數;P為渦旋體節距。

(3)排氣腔容積。隨著曲軸的轉動，當轉過6π+θ*弧度時，第二壓縮腔與中心排氣腔相連通成為一個腔體。當θ∈(6π+θ*,8π)時，渦旋壓縮機開始對剛剛壓入中心排氣腔的氣體進行排氣，排氣腔容積

(6)

隨曲軸的轉動，當θ∈(8π,8π+θ*)時，排氣角打開，進入排氣階段，腔內的容積

(7)

(8)

2 熱力學模型

建立無油渦旋壓縮機的熱力學模型，需充分考慮吸氣加熱和工作腔之間的傳熱模型，以及徑向泄漏和切向泄漏兩種內泄漏對熱力學模型的影響，揭示氣體在實際工作狀況下的變化規律。

2.1 基本方程

在工作狀態下，腔內氣體的溫度隨曲軸轉角變化的基本方程為[13]

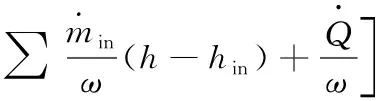
(9)

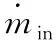
腔內氣體質量隨曲軸主軸轉角變化的基本方程為

(10)

2.2 傳熱

存在溫差的環境中必然會發生熱傳遞現象，熱傳遞有熱傳導、熱對流、熱輻射三種方式。介質氣體進入吸氣腔后，介質氣體與腔內發生比較復雜的熱傳遞過程，為了簡化傳熱模型，忽略熱傳導和熱輻射，只考慮熱對流現象。

2.2.1吸氣加熱

吸氣按照流體在管內熱對流來計算，采用Dittus-Boelter方程，表面傳熱系數[14]

hc=0.023κRe0.8Pr0.4/dp

(11)

式中，κ為熱導率；dp為管徑；Re為雷諾數；η為流體黏度；cp為介質的定壓質量熱容；Pr為普朗特數。

被壓縮的氣體從吸氣口進入工作腔內部的溫度為

(12)

式中，Tp為吸氣管溫度；Ts,o為介質進入吸氣管的溫度；Lp為吸氣管長度。

則介質氣體與輸氣管的傳熱量

(13)

2.2.2工作腔傳熱

對于無油渦旋壓縮機，在建立傳熱模型時不考慮潤滑油的溫度對渦旋齒的影響以及潤滑油和渦旋齒之間的傳熱模型。采用螺旋板式換熱器平均對流模型來計算氣體與渦旋齒的傳熱過程，則渦旋盤的熱交換系數[15-16]

[1+8.48(1-exp(-5.35St))]

(14)

式中，St為斯特勞哈爾數；Raver為平均半徑。

其中，當量直徑Def定義為工作腔容積與渦旋齒壁的比值：

Def=4V/A

(15)

式中，A為工作腔面積。

則當量半徑定義為

(16)

式中，φk、φk-1分別為工作腔兩端的漸開角。

2.2.3傳熱面積

渦旋齒之間的傳熱面積在漸開角為φk到φk-2π范圍內的表達式

dA=hcrb(φ-φ0)dφ

(17)

則渦旋盤底部的傳熱面積的表達式

(18)

氣體在渦旋齒、渦旋盤底部的換熱量，在任意工作腔中的表達式[17]

(19)

式中，Tscr(φ)為中間溫度；T(k,j)為第k工作腔在θj的溫度；dA為傳熱面積。

2.3 泄漏

渦旋壓縮機存在兩種不同的泄漏模型，即通過軸向間隙的徑向泄漏和通過徑向間隙的切向泄漏。對于壓縮機的兩種內泄漏分析，可以得到徑向泄漏面積[18]

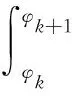
(20)

式中，L為徑向泄漏線長度；δr為徑向泄漏間隙；pH為高壓側壓力；pL為低壓側壓力。

δr可以寫成關于壓力比的線性函數：

δr=1.1×10-6(pd/ps)+10-6

(21)

式中，pd為排氣腔壓力；ps為吸氣腔壓力。

切向泄漏面積

Af=Hδf(pH,pL)

(22)

軸向泄漏間隙δf也可寫成關于壓力比的線性函數：

δf=-9.615×10-5(pH/pL-1.67)+20×10-6

(23)

渦旋壓縮機的泄漏可以抽象成為一種噴嘴模型，在模擬計算工質氣體為空氣，則腔體內氣體的質量流量[19]

(24)

(25)

式中，ψ為流動系數；As為截面面積；ρH為高壓側密度；γ為壓縮指數。

2.4 理論排氣量

渦旋壓縮機的理論排氣量Qh為行程容積V0與轉速nc的乘積：

(26)

式中，ηv為容積效率；Qg為實際排氣量，m3/min；nc為壓縮機轉速；N為渦旋型線的任意圈數；θS為吸氣結束角；int(N)為N的取整函數。

2.5 軸功率

新型無油渦旋壓縮機的軸功率[20]

(27)

式中，n為曲軸轉速；t′為曲軸旋轉一周的時間；Tshaft為曲軸轉矩。

3 模擬分析

依據構建的新型無油渦旋壓縮機的熱力學模型，借助Fortran和MATLAB軟件對模型進行編程求解，新型無油渦旋壓縮機熱力學模型的求解流程見圖3。輸入無油渦旋壓縮機的幾何參數，采用積分法編程求解容積隨主軸轉角的變化規律。基于熱力學第一定律和能量守恒方程，綜合考慮工作腔內部的兩種內泄漏模型以及吸氣加熱和工作腔之間的兩種傳熱模型，采用歐拉法計算在不同的傳熱量和泄漏量的情況下，工作腔內部氣體的質量、溫度和壓力隨主軸轉角的變化規律，進一步研究和探索不同的傳熱量和泄漏量對新型無油渦旋壓縮機性能的影響規律。

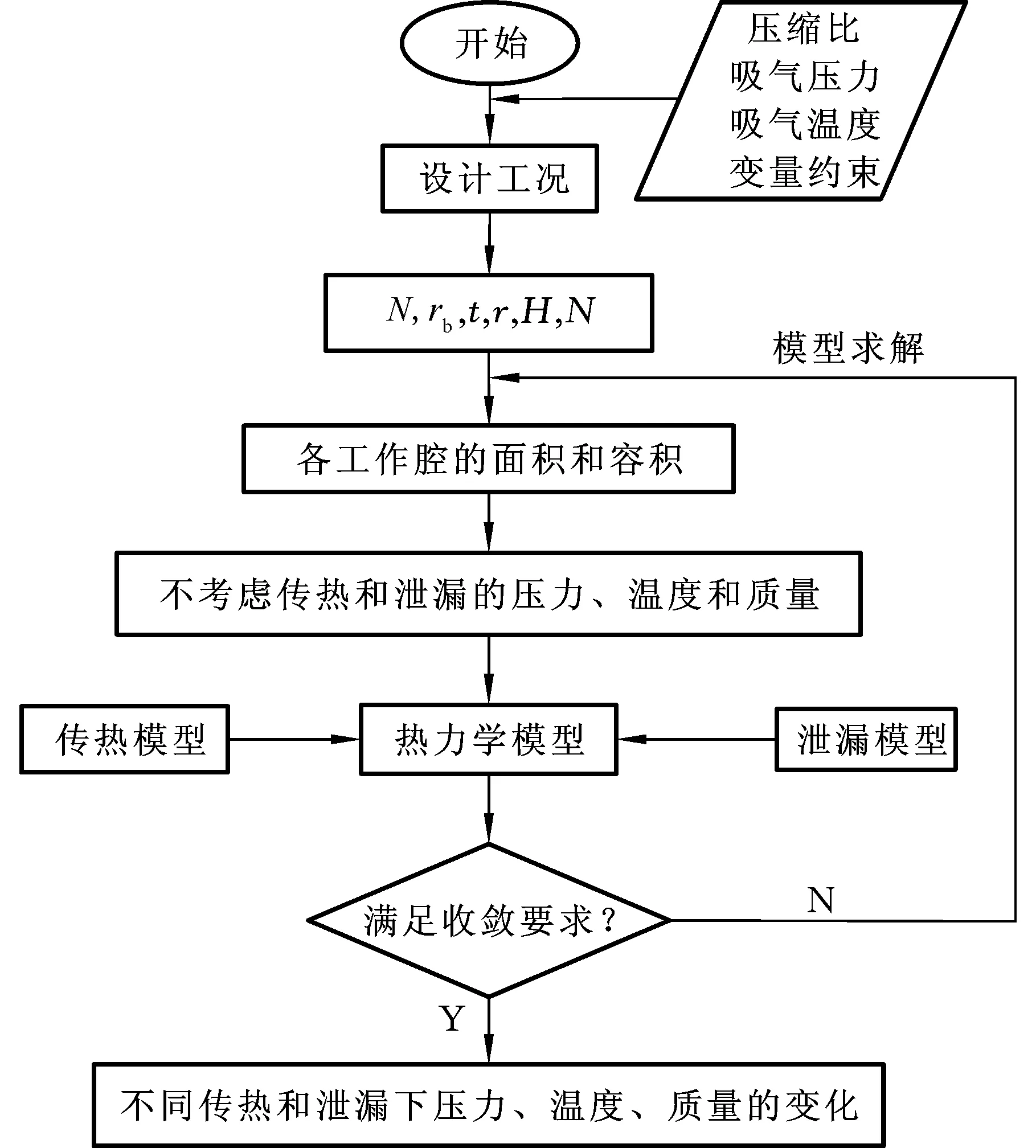
圖3 熱力學模型的求解流程Fig.3 Thermodynamic model of the solution process

3.1 工作腔容積變化規律

無油渦旋壓縮機工作腔容積的變化曲線見圖4。氣體從吸氣口進入吸氣腔，直至吸氣腔閉合，完成一次吸氣過程。容積的變化是先增加到最大值2.139×105mm3，然后略微減小。隨主軸轉角的增大，腔內的氣體連續被壓縮，此時容積不斷減小，直至主軸轉角達到排氣角時，壓縮機開始排氣。排氣腔內的容積進一步減小，直到排氣結束，完成整個吸氣-壓縮-排氣全過程。從圖4中可以明顯看出，壓縮腔內容積是一個連續變化的過程，其容積變化率可以直觀地反映在圖5中。

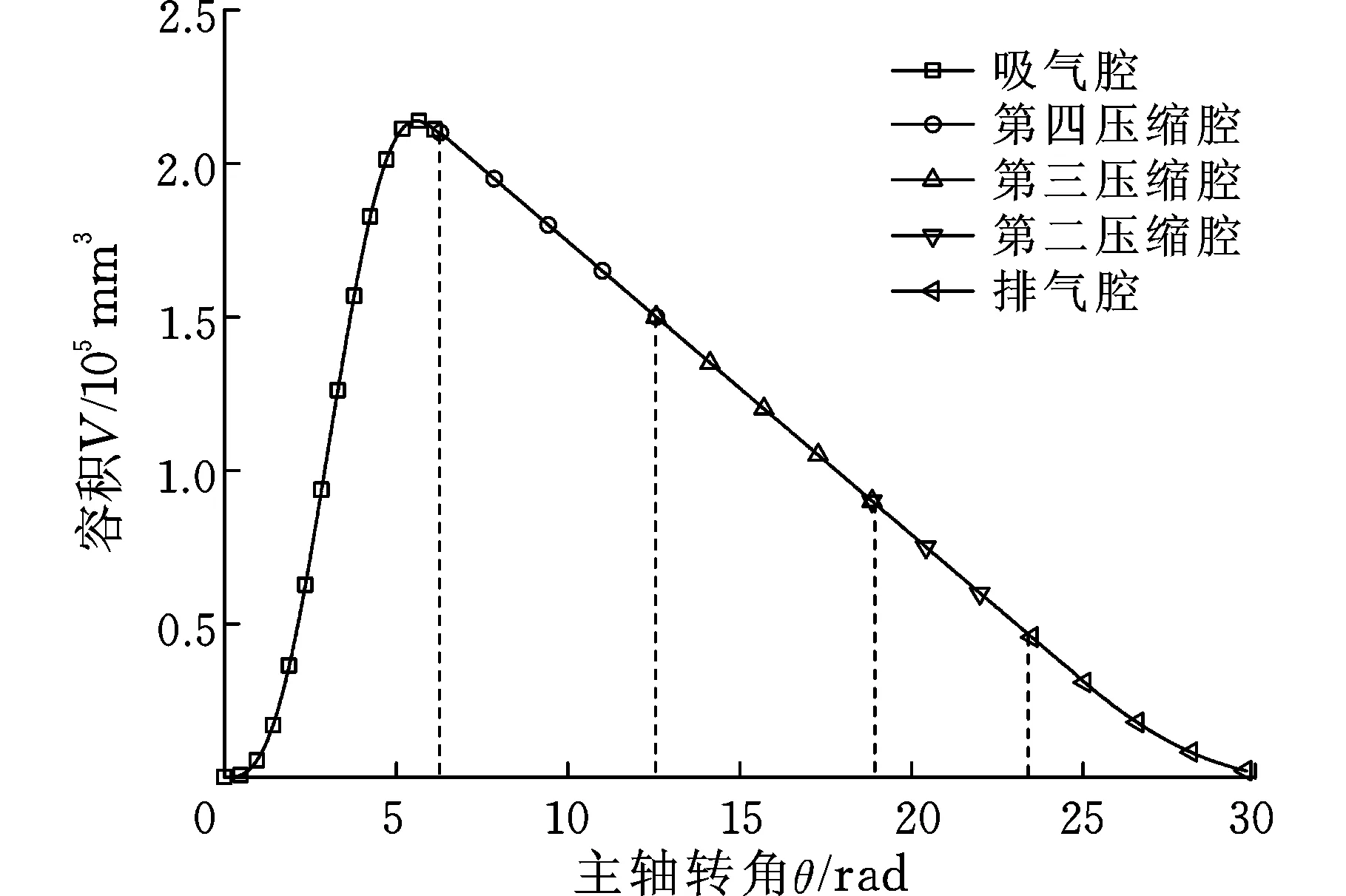
圖4 容積隨主軸轉角的變化Fig.4 Volume variety with the spindle angle

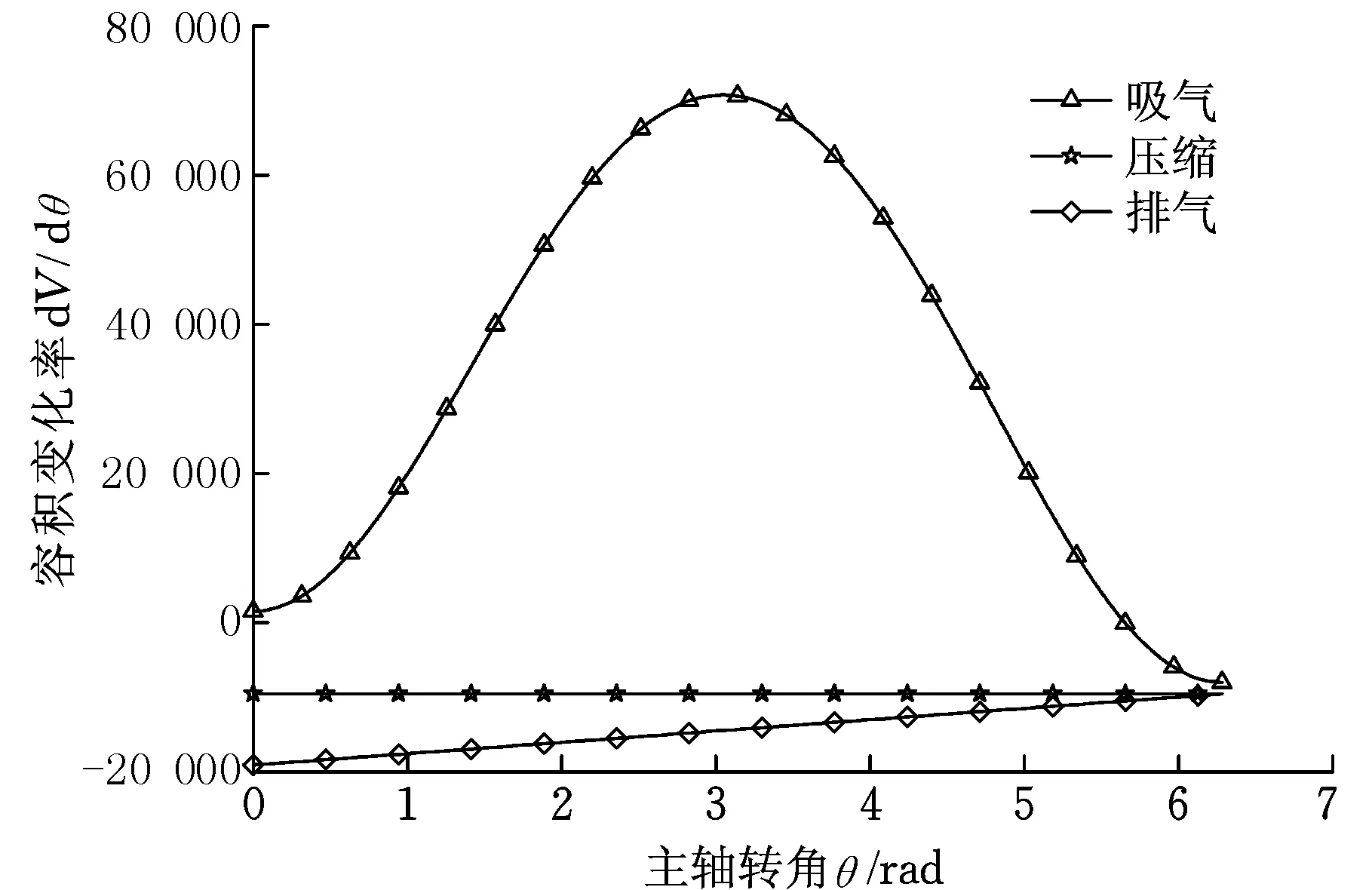
圖5 容積變化率Fig.5 Volume variety rate

工作腔的容積變化率見圖5。在吸氣階段，容積變化較快；在壓縮過程中，容積的變化率基本保持不變；而在排氣階段，容積的下降速率很快，這是由于排氣孔口已經打開，高溫高壓的氣體迅速排出到外界。

3.2 工作腔壓力變化規律

工作腔內壓力的變化曲線見圖6。在吸氣結束前，不考慮傳熱和泄漏，壓力幾乎保持不變。隨著工作腔內的容積的繼續減小，氣體的壓力不斷增大。在僅考慮傳熱的情況下，壓力的變化幅度最大，為101～780 kPa。不考慮泄漏的壓力變化比考慮泄漏的變化更大，這是因為在不考慮泄漏的影響時，質量流量比是一常數，導致壓力瞬間達到最大值。排氣孔剛打開的瞬間，壓力會出現突變，隨著排氣孔完全打開，壓力基本上維持在某一穩定的數值，在排氣階段，傳熱和泄漏對壓力的變化影響不大。

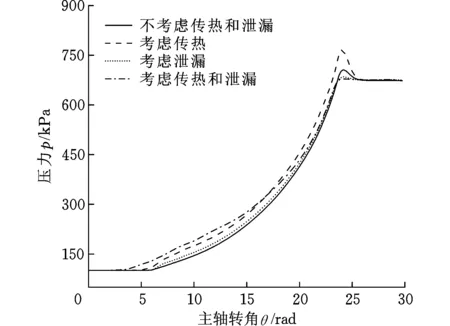
圖6 壓力隨主軸轉角的變化Fig.6 Pressure changes with the spindle angle

3.3 工作腔溫度變化規律

工作腔內溫度的變化曲線見圖7。氣體在進入壓縮機的吸氣腔前，吸氣管道對氣體有吸氣加熱的效果，會有2～3oC的溫升變化。在壓縮階段，僅考慮傳熱的情況下，溫度的變化最大，從17 ～187oC變化。考慮熱傳遞的影響時的溫度比未考慮熱傳遞時的溫度更高，這是由于工作介質吸收從高壓側傳遞給渦旋齒壁面的溫度，導致溫度升高。在排氣階段，溫度的變化和壓力變化類似，先增大后略微減小，最終保持恒定。

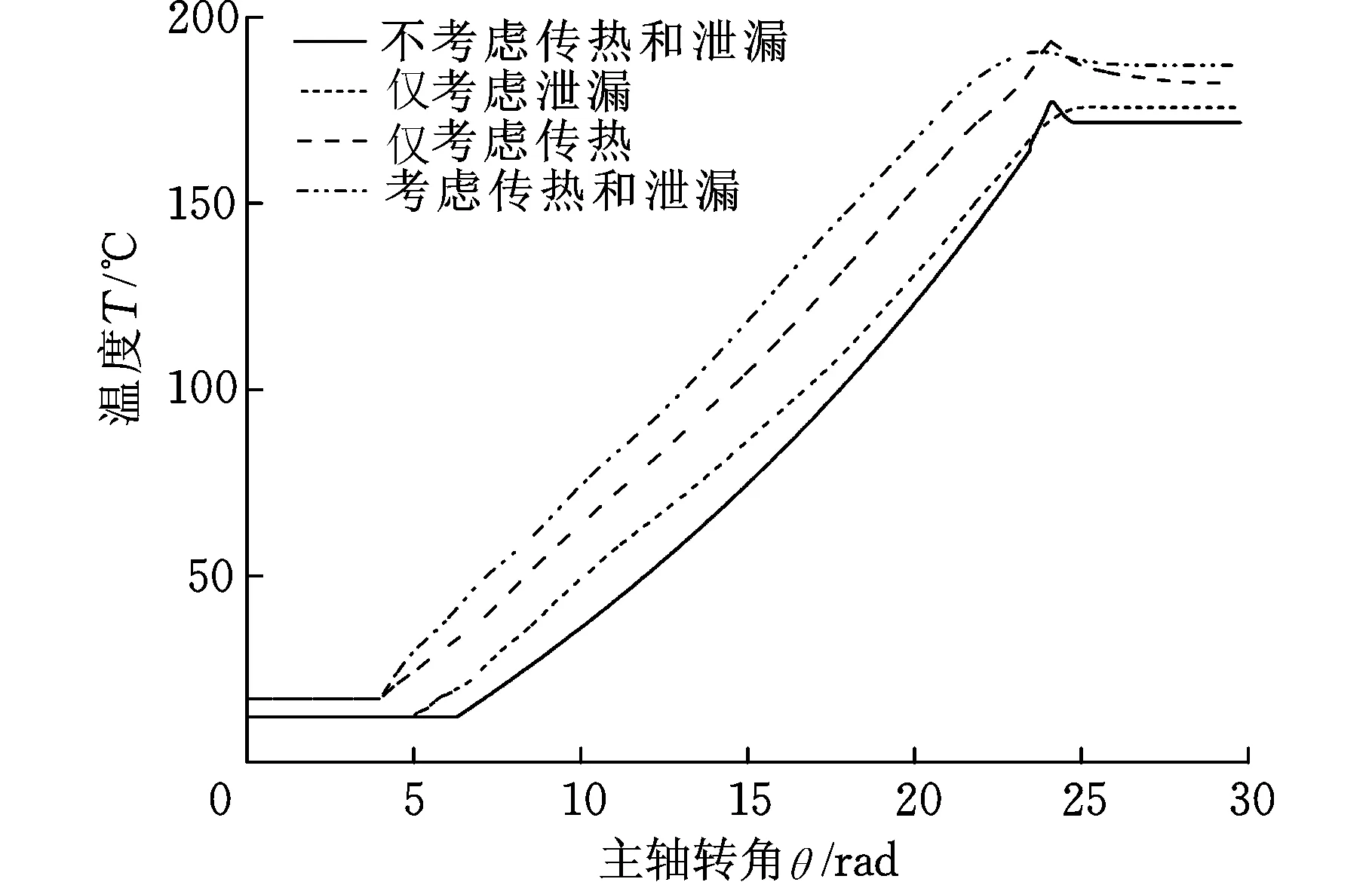
圖7 溫度隨主軸轉角的變化Fig.7 Temperature variety with the spindle angle

3.4 工作腔質量變化規律

工作腔內質量變化曲線見圖7。在吸氣終了時刻，同時考慮傳熱和泄漏的質量最小，不考慮傳熱和泄漏時的質量最大。由于工作腔內存在泄漏，導致質量不斷減小。在不考慮泄漏時，壓縮腔內的質量保持一恒定值，直到排氣孔口打開，質量迅速減小。僅考慮泄漏時，質量先略微增大，后整體減小。在壓縮過程中，由于徑向泄漏較大，使得在考慮泄漏的影響時，質量急劇減小，同時考慮傳熱和泄漏時的質量是最小的。介質進入排氣腔，隨排氣孔的打開，腔內的質量也迅速減小，直至排氣結束。

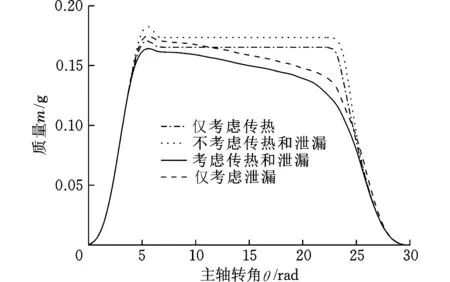
圖8 質量隨主軸轉角的變化Fig.8 Mass changes with the spindle angle

4 試驗

為驗證新型無油渦旋壓縮機熱力學模型的準確性，分析不同工況下整機的性能，本文研制開發了新型無油渦旋壓縮機的樣機，測量在不同排氣壓力下排氣溫度、功率以及排氣量的變化，來評價樣機的性能是否達到設計要求，能否滿足工業應用的要求。測試樣機實物見圖9a，依據測試系統原理圖(圖9b)搭建了無油渦旋壓縮機的測試平臺，并將模擬與測試數據進行了對比。本試驗數據的測試是嚴格參考最新版的GB/T 3853-1998《容積式壓縮機驗收試驗》和GB 19153-2009《容積式空氣壓縮機能效限定值及能效等級》標準執行的。

圖9 測試樣機及測試平臺Fig.9 Test platform

不同壓力條件下，溫度隨主軸轉速的變化曲線見圖10。可以看出，當排氣壓力相同時，隨主軸轉速的增大，排氣溫度不斷升高。在主軸達到相同轉速時，隨排氣壓力的增大，排氣溫度也不斷上升。

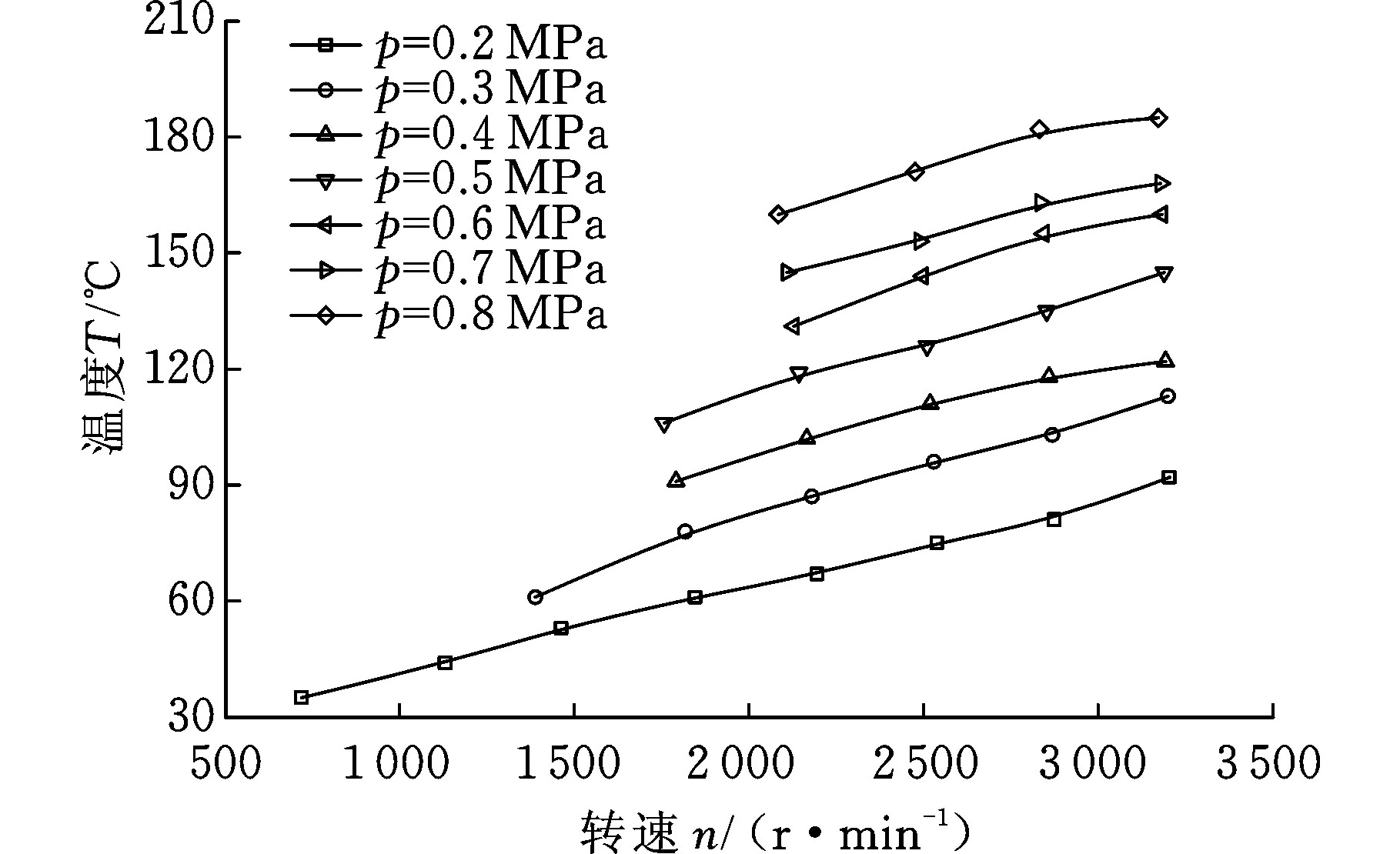
圖10 不同壓力條件下溫度隨轉速的變化Fig.10 Temperature variety with speed under different pressure

排氣壓力為0.2 MPa時，模擬與試驗排氣量的比較見圖11。轉速較低時，模擬計算的排氣量與試驗測得的數據之間存在較大偏差，這是由于在低轉速時，氣體在腔體內停留的時間較長，有一部分氣體發生泄漏；而在高轉速時，吸入的氣體快速排出到外界，因此，高轉速時模擬與試驗測得的數據比較接近。測試數據表明，在構建熱力學模型的過程中，對兩種泄漏模型以及傳熱模型的分析是合理的。

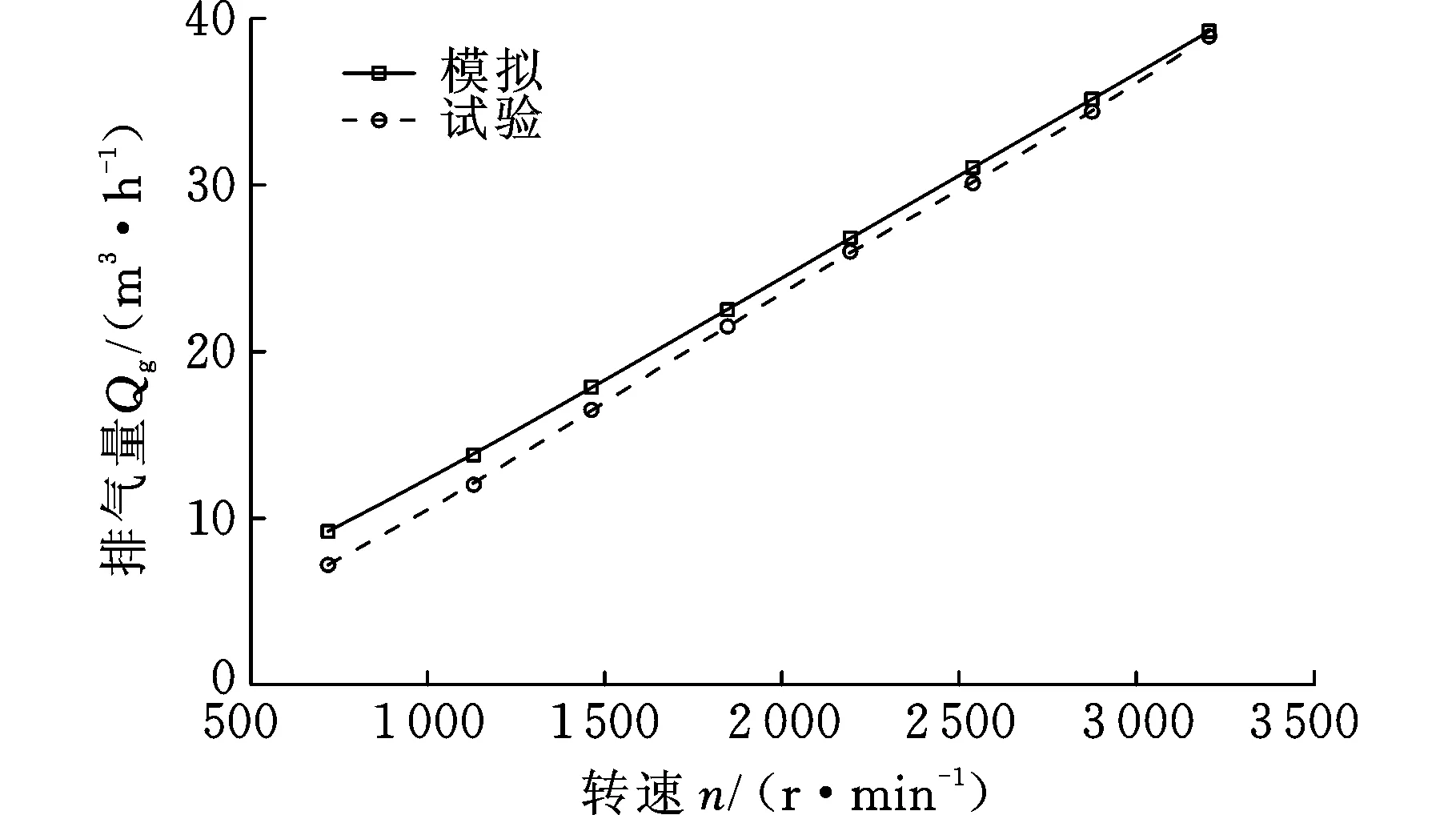
圖11 試驗與模擬排氣量的比較Fig.11 Comparison of test and simulated displacement

不同壓力條件下，排氣量隨主軸轉速的變化曲線見圖12。可以看出，當排氣壓力相同時，隨主軸轉速的增大，排氣量不斷增大。在主軸達到同一轉速時，隨著排氣壓力的持續增大，排氣量略微減小。由圖12可知，排氣壓力對排氣量的影響較小，不同排氣壓力下，排氣量的變化幅度不大。

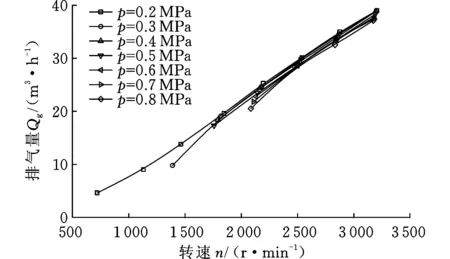
圖12 不同壓力條件下排氣量隨轉速的變化Fig.12 Displacement variety with speed under different pressure

模擬與試驗軸功率的比較見圖13。隨轉速的增大，模擬軸功率與試驗測得的數值均呈增大的趨勢，且兩者的誤差相對較小，從而驗證了熱力學模型的準確性。

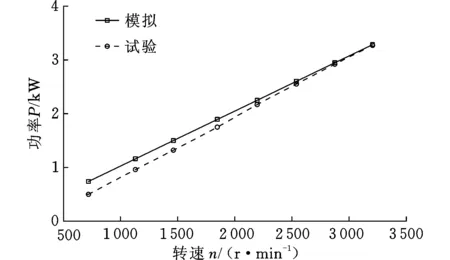
圖13 模擬與試驗軸功率比較Fig.13 Comparison of simulation and test shaft power

不同壓力條件下功率隨轉速的變化曲線見圖14。可以看出，在排氣壓力相等的情況下，隨主軸轉速的增大，功率不斷增大；同一主軸轉速下，隨排氣壓力的增大，功率也逐漸增大。

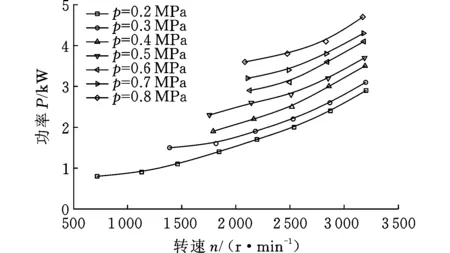
圖14 不同壓力條件下功率隨轉速的變化Fig.14 Power variety with speed under different pressure

5 結論

(1)綜合考慮徑向泄漏和切向泄漏以及吸氣加熱和對流傳熱模型，建立了無油渦旋壓縮機的熱力學模型。

(2)采用歐拉法對建立的熱力學模型求解，得到了氣體在不同傳熱和泄漏條件下的溫度、壓力和質量的變化規律。

(3)通過對建立的熱力學模型計算得出：傳熱對壓力和溫度的變化影響最大，而泄漏對質量的變化影響最大。相比有油的渦旋壓縮機，無油渦旋壓縮機具有更高的功率。

(4)測試結果表明：在不同的排氣壓力下，溫度、功率變化幅度較大，而排氣量的變化幅度較小。該試驗數據對新型無油渦旋壓縮機的研究和性能分析具有一定的指導和借鑒作用。研究結果可為無油渦旋壓縮機的理論研究及原創型的新能源汽車供氣系統研制方面提供基礎和技術儲備，真正實現能源的高效利用。