介電濕潤芯片上液滴從靜止到運動的機理

許曉威 孫立寧 張玉良 江海兵

1.衢州學院機械工程學院,衢州,324000 2.蘇州大學機器人與微系統研究中心,蘇州,215021

0 引言

近年來,微流控技術隨著微制作工藝的快速發展取得了很大的突破。在微流控領域中利用介電濕潤(electrowetting-on-dielectric, EWOD)機理已經成為一種趨勢。目前基于介電濕潤機理操控液滴的技術被稱為數字微流控技術，包括從儲液池中生成液滴、把一個液滴分離成兩個子液滴、把兩個液滴合并成一個液滴以及液滴的運輸四項基本操控[1-4]。數字微流控技術不需要微泵、微閥和微管道等復雜的機械結構，避免了結構復雜部件的制作和裝配、不同液體的交叉使用所造成的污染、液體堵死等現象。數字微流控芯片可以操控μL甚至nL級別的單個微液滴,使其在“芯片上實驗室”(lab on a chip)中得到越來越多的應用[5-12]。另外，數字微流控技術在光學[13]、芯片降溫[14]、傳感器[15]等領域也得到了廣泛的應用。

數字微流控技術中液滴在電場的作用下經過一系列過程而運動，該過程是多尺度、多階段的。總結相關文獻發現，研究者針對EWOD芯片上液滴從靜止到運動的過程和機理提出了各種假設[16-21]，而該機理至今未見系統的研究。本文在前人研究的基礎上，通過理論分析、數值仿真和實驗研究，針對液滴從靜止到運動的過程進行研究。

1 介電濕潤基本機理

數字微流控技術中常用的結構為圖1a所示的“三明治”結構，液滴位于上下極板之間[1,4]，施加驅動電壓前液滴位于左右驅動電極之上，由于上下極板表面涂有厭水層，液滴的初始接觸角θ0接近120°，液滴近似為球形。數字微流控技術操控液滴運動是通過給介電層下方的驅動電極通電來實現的。如圖1b所示，液滴由圖1a中的近似球形形狀變成圖1b所示的不規則形狀，此時右側驅動電極通電，液滴的大部分位于左側不加電驅動電極之上，位于通電驅動電極之上的液滴初始接觸角θ0減小，當減小量足夠大時，液滴就會向通電驅動電極的方向運動。按時序分別給陣列驅動電極通電，液滴就會按照規劃好的路徑運動。數字微流控技術包括液滴的生成、分離、合并和運輸四項基本操控[1-6]。驅動電壓與接觸角的關系可由楊-李普曼方程表述：

(1)

式中，θU、θ0分別為液滴在施加驅動電壓U時的接觸角和不施加驅動電壓時的初始接觸角；εr、ε0分別為介電濕潤芯片介電層的相對介電常數和真空介電常數；γlg為“氣-液”表面張力；d為芯片的介電層厚度。

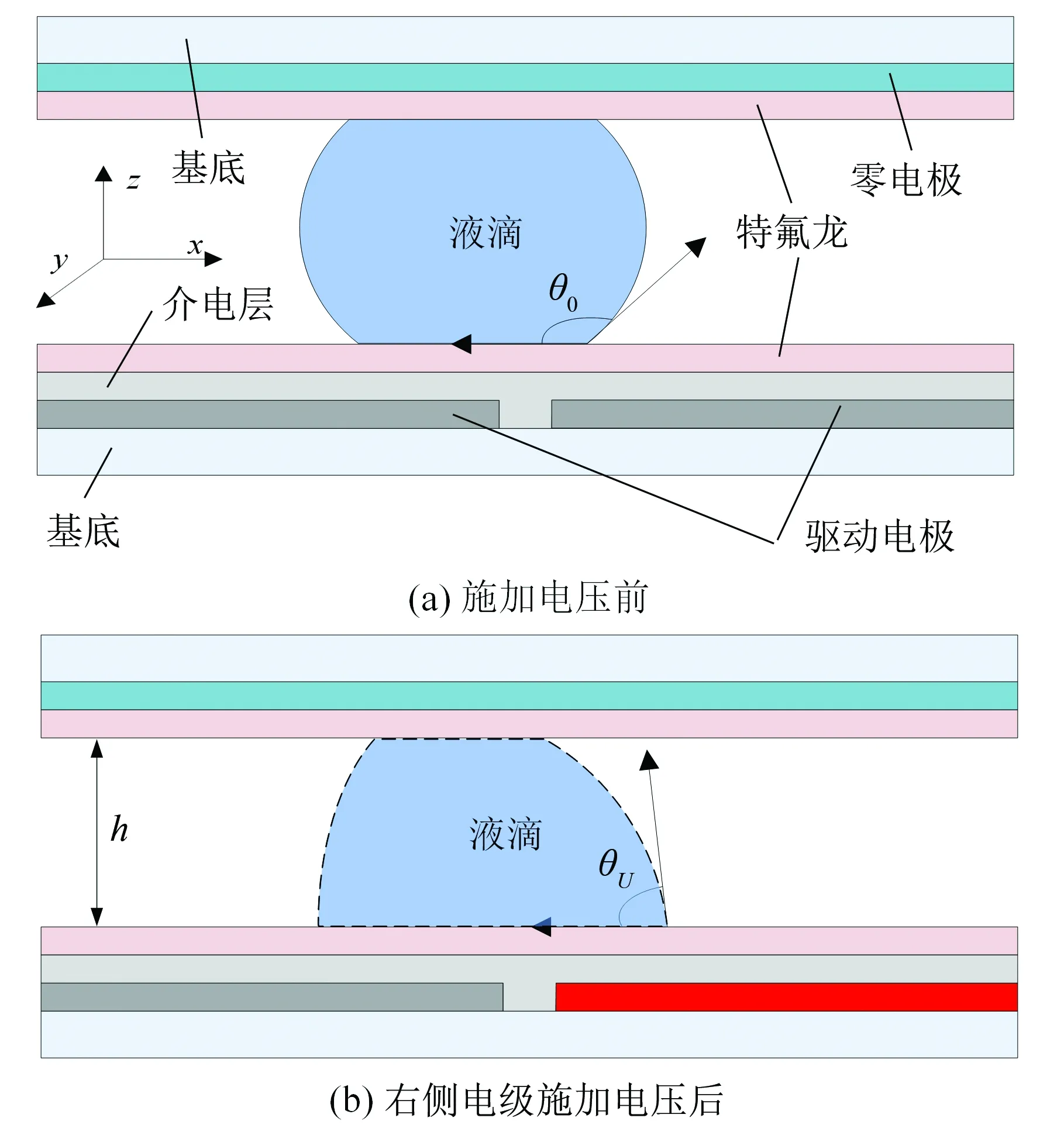
圖1 介電濕潤基本原理示意圖(側視圖)Fig.1 Schematic diagram of electrowetting-on- dielectric basic principle (side view)

2 固液接觸面極化機理

在電磁學領域，在外電場作用下，電介質會顯示電性。理想的絕緣介質內部沒有自由電荷，而實際上，電介質內部總是存在少量的自由電荷，它們是造成電介質漏電的原因。一般情況下，未經電場作用的電介質內部的正負束縛電荷處處抵消，宏觀上并不顯示電性。而在外電場作用下，束縛電荷的局部移動會導致宏觀上顯示電性，在電介質的表面和內部非均勻的部分出現電荷,這種現象稱為極化，出現的電荷稱為極化電荷，這些極化電荷會改變原來的電場。因極化而產生的電偶極子稱為“感應電偶極子”，其電偶極矩稱為“感應電偶極矩”。電極化強度矢量P也稱為電極化矢量，其大小為電介質內的電偶極矩密度，也就是單位體積的電偶極矩，又稱為電極化密度。該定義所指的電偶極矩包括永久電偶極矩和感應電偶極矩。電極化強度P、電場強度E、電位移D這三個矢量的關系表達式為

D=ε0E+P=ε0εrE

(2)

對于各向同性、線性電介質，電極化強度P和電場強度E的比例稱為電極化率χe，有

P=χeε0E

(3)

所以，電位移與電場強度成正比，即

D=ε0(1+χe)E=εE

其中，ε為電容率(介電常數)。相對電容率εr(相對介電常數)與電極化率的關系為

εr=1+χe

電極化強度P、電場強度E、電位移D三個矢量的方向相同。電磁學所描述的物理量大部分都是宏觀的平均值，像電場平均值、電極化強度平均值等都是取自一個遠大于原子尺寸的區域。當研究微觀問題時，對于在電介質內的單獨粒子，其極化性與電極化率平均值、電極化強度平均值的關系可用克勞修斯-莫索提方程來表達：

(4)

式中，Nj為分子j的每單位數量的面積;αj為分子j的分子極化率。

式(4)表達了分子極化性與介電常數的關系。該式在微觀量(極化性)和宏觀量(介電常數)之間建立起了一個連接，是連接微觀世界與宏觀世界的“橋梁”。式(4)有助于在分子層面上進一步理解介電濕潤芯片上液滴驅動的本質——固液接觸面在電場下的作用機理。

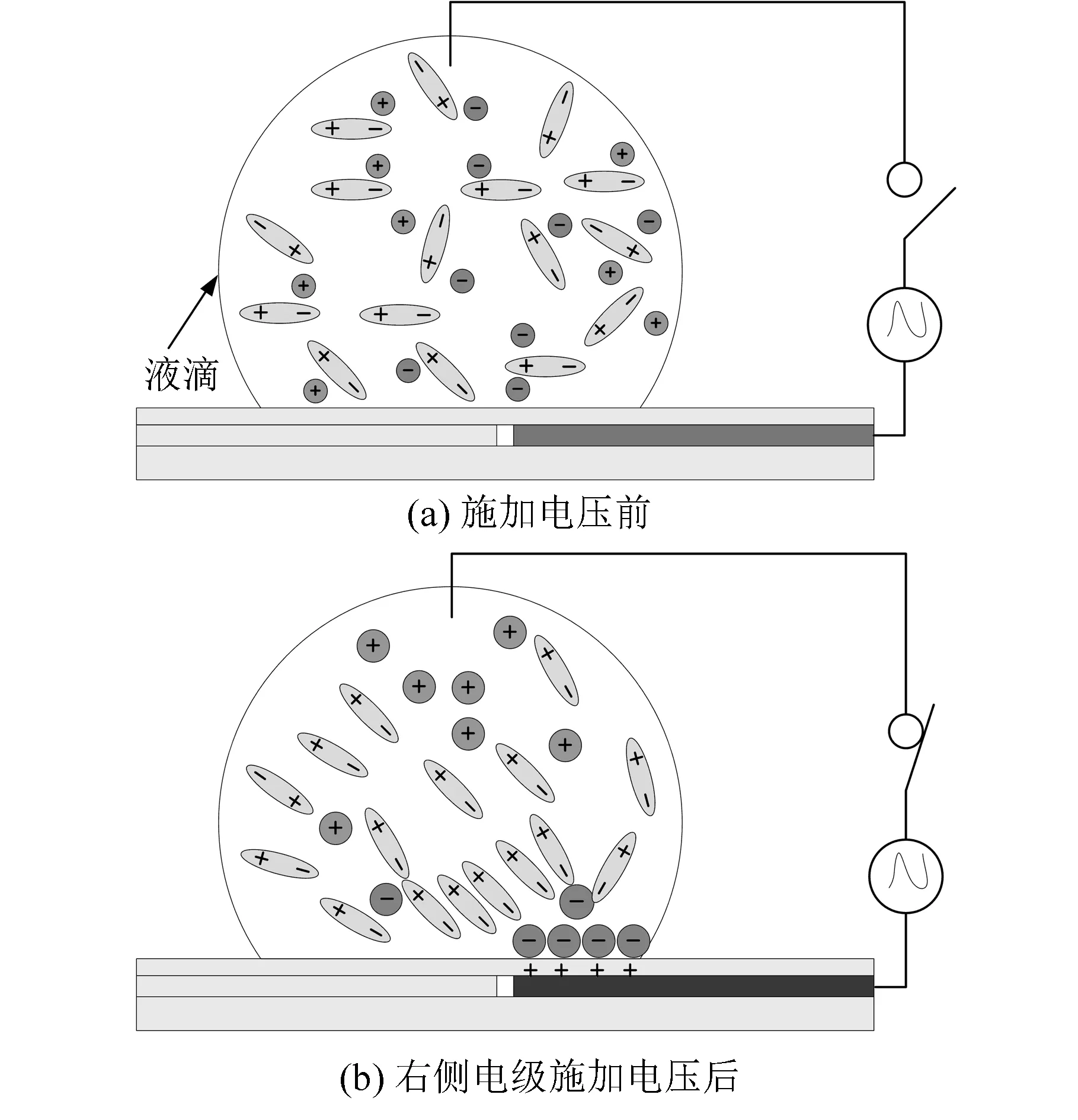
圖2 電荷與電偶極子變化情況示意圖(側視圖)Fig.2 Schematic diagram of the change in charge and electric dipole (side view)

在圖2所示的EWOD芯片中，當右側驅動電極不導通時(圖2a)，液滴中的電偶極子和自由電荷隨機分布在液滴中。當右側驅動電極導通時(圖2b)，在驅動電極與零電極之間形成電場，在電場作用下，厭水層表面會聚集大量的正電荷而成為表面束縛電荷，在這些表面束縛電荷的作用下，根據異性相吸的原理，液滴內靠近束縛電荷表面的帶負電的自由電荷與電偶極子帶負電的部分會被吸引到該表面。宏觀上，液滴位于導電驅動電極上方的厭水層表現出親水性，位于該部分之上的液滴接觸角會減小。這一過程液滴受到靜電力作用，靜電力是導致液滴接觸角改變的主要原因。

3 數值仿真及實驗研究

3.1 介電驅動力

采用COMSOL Multiphysics 4.4多物理場仿真軟件對圖1b和圖2b中的電場進行數值仿真，相關模型參數見表1。

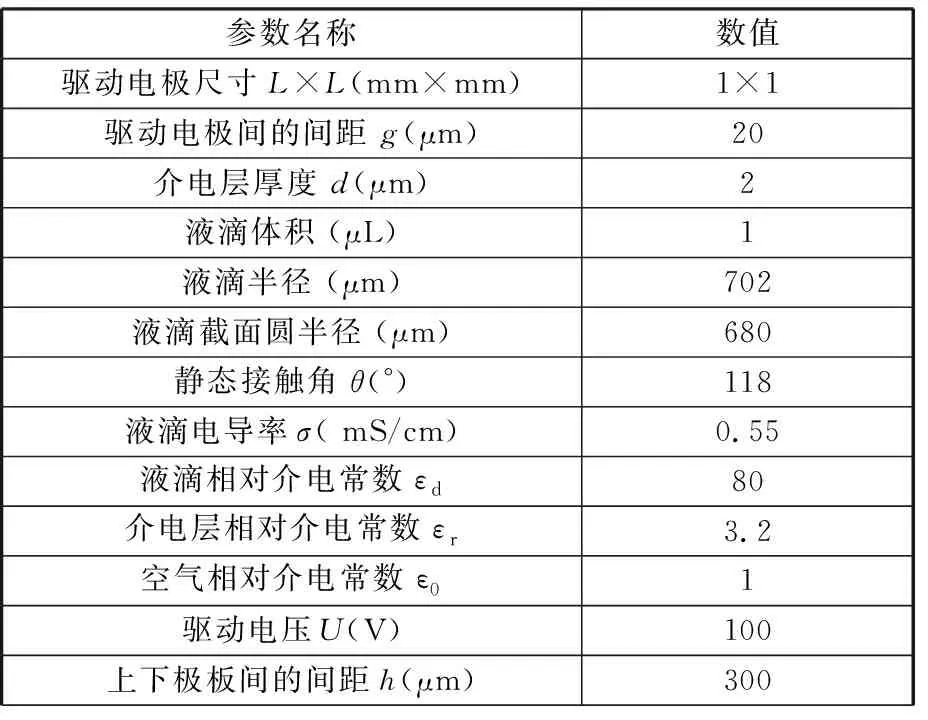
表1 數值仿真模型相關參數

在進行數值仿真時可把液滴近似看作介電體，根據電荷守恒定律和拉普拉斯方程[9]得到

(σU)=0

(5)

(6)

外加電壓在液滴附近產生靜電場，由該電場引起的介電驅動力分量為

(7)

式中，Fi為空間直角坐標系中第i個坐標的介電驅動力分量；Tij為麥克斯韋應力張量元;sj為第j個坐標方向上液滴的表面積；Σ表示積分區域為液滴表面。

由張量運算規則可知對于每一個麥克斯韋應力張量元，有

(8)

式中，Ei、Ej分別為空間直角坐標系中第i和第j個坐標方向的電場強度；δij為Kronecker函數。

由高斯環路定理可得麥克斯韋應力張量為

(9)

ε=εrε0

式中，I為二階單位張量。

把麥克斯韋應力張量改寫成矩陣形式如下：

T=

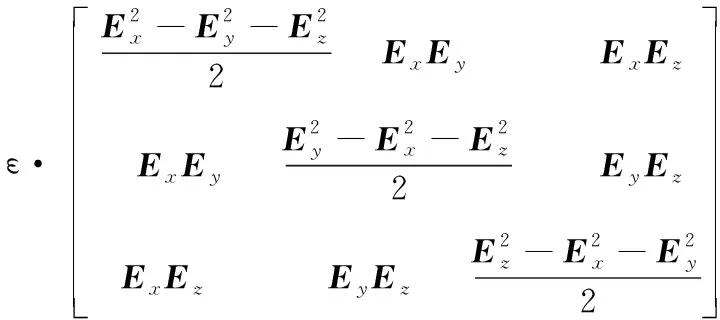
(10)

利用高斯定理求得圖1中液滴在x、y、z三個方向所受介電驅動力為

(11)

式中，V為液滴的體積。

由于y、z方向的介電驅動力對液滴運動影響較小，可忽略不計，所以液滴所受介電驅動力可簡化為液滴在x方向上的受力。

圖3所示為“液滴-驅動電極-介電層-介質”所組成的系統劃分好網格后的三維模型。為簡化運算，本文數值仿真只選取了左右兩個驅動電極，選擇空氣作為介質。

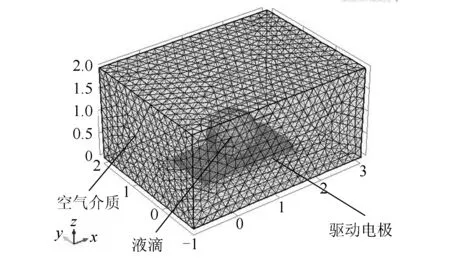
圖3 液滴三維仿真模型Fig.3 Three-dimensional simulation model of droplet

圖4a為右側驅動電極導通時的電勢分布圖，為更直觀地表示驅動電極導通后的電勢分布情況，此圖后處理過程中選擇切片模式。很明顯，右側驅動電極上的電勢接近100 V。圖4b為固液接觸面電場強度分布圖，箭頭的長短表示該箭頭所處位置電場強度的大小，很明顯，液滴截面圓位于右側驅動電極之上的電場最強，該部分電場集中分布，電場的方向指向零電極。圖4c為固液接觸面上麥克斯韋應力張量分布圖,箭頭的長短表示麥克斯韋應力張量的大小，很明顯，液滴截面圓位于右側導電驅動電極之上的麥克斯韋應力張量是最密集和最大的。

根據麥克斯韋理論，電場是傳遞力的“橋梁”，電荷之間所產生的庫侖力靠電場來進行傳遞。驅動電極導通時會在介電濕潤芯片與液滴所組成的系統中產生電場，計算出總的電場分布之后就可以推導出麥克斯韋應力張量。根據上文液滴所受介電驅動力(式(11))可知，麥克斯韋應力張量是計算EWOD芯片中液滴所受介電驅動力的一個橋梁，計算出麥克斯韋應力張量，就可以算出液滴所受介電驅動力。同理，圖4c把固液接觸面上液滴受到的麥克斯韋應力張量用箭頭直觀地表示出來了，該結果和前文中液滴受到靜電力的理論分析可以相互印證。

圖4d為驅動電極表面的極化效應數值仿真圖。在電場的作用下，介電層材料與液滴間會表現出異性電荷相互吸引的趨勢。EWOD芯片系統中介電層材料與液滴的分子原來是沒有電偶極矩的，在外電場作用下，構成分子的正負電荷發生相對位移，形成電偶極子，具有一定的電矩，其方向沿著外電場的方向，所以在固液接觸面上，分別出現了正負束縛的表面電荷。圖4d中的箭頭正是把“極化”這一抽象概念形象地表示出來了，圖中較大的箭頭集中于液滴截面圓之內，這說明在電場的作用下該部分是有“極化效應”存在的。首先，位于導電驅動電極上方的固液接觸面在電場的作用下產生“極化效應”，這一過程液滴受到靜電力作用，然后，該部分固液接觸面形成表面束縛電荷后使液滴的表面張力平衡狀態遭到破壞，不再平衡的表面張力使液滴產生一定量的形變，液滴的形變會使液滴內部產生壓力差，而該壓力差即為驅動液滴運動的力。

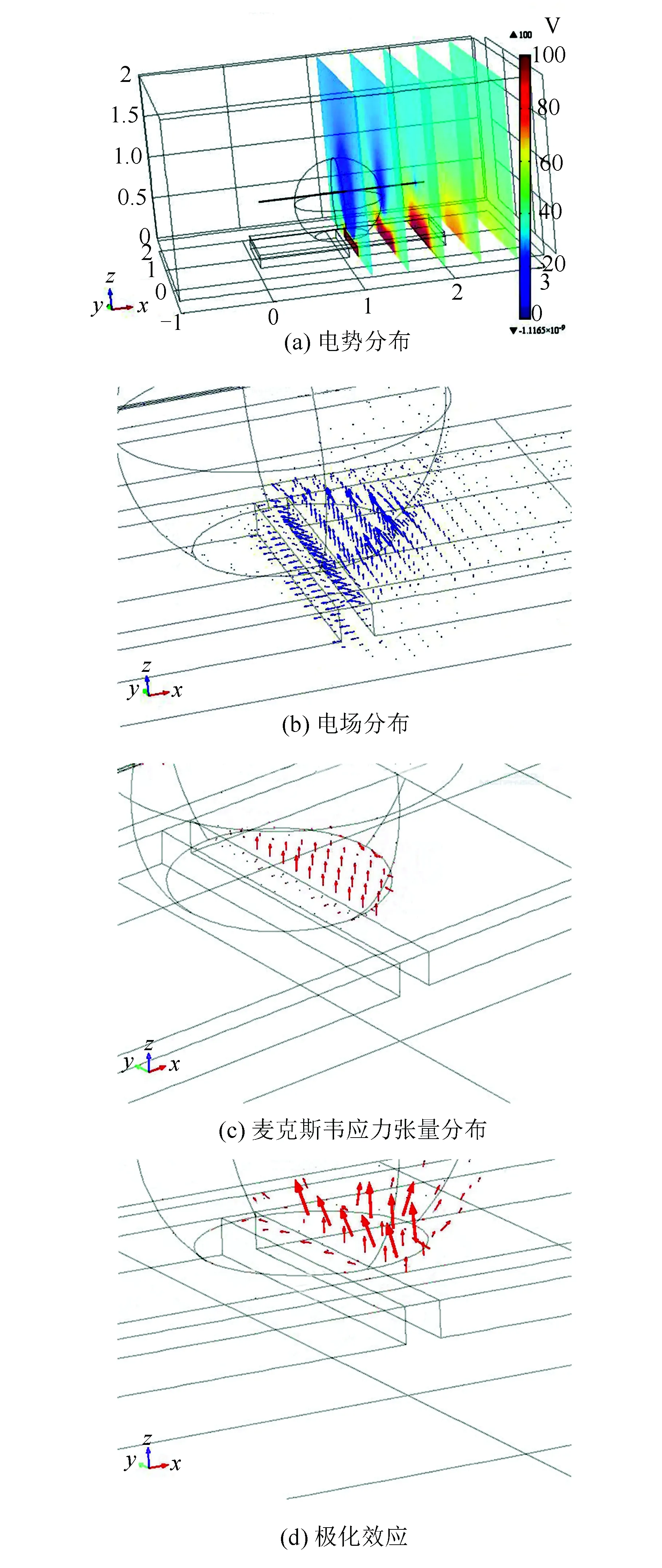
圖4 電場數值仿真結果Fig.4 Numerical simulation results of electrical field

3.2 驅動機理及實驗驗證

圖5a中，液滴恢復部分和前進部分的曲率半徑分別為[17]

(12)

(13)

式中，θ0、θU分別為液滴恢復部分和前進部分的接觸角，即初始接觸角和施加驅動電壓U時的接觸角；θt為液滴與上極板接觸時的接觸角；h為上下極板間的間距。

根據拉普拉斯方程，位于液滴恢復部分與前進部分的兩個隨機點1和2處的壓力p1和p2分別為

(14)

(15)

式中，R1、R2分別為液滴恢復部分和前進部分的半徑；pg為空氣介質壓力。

那么可以推導出液滴內部1和2兩個隨機點處流體靜壓力差計算式為

(16)

由圖5a可知，液滴恢復部分曲率半徑小于前進部分曲率半徑，即γ1<γ2；液滴恢復部分半徑小于前進部分半徑,即R10。因此，液滴恢復部分與前進部分各點處的壓力差之和即近似為液滴內部總的流體靜壓力差：

pi≈p1-p2

此壓力差計算式忽略液滴的接觸角滯后和液滴周圍介質對液滴的黏性阻力，是一個理想狀態下的估算數學模型。

圖5b為液滴內部壓力最大區域隨驅動時間在液滴內部轉移示意圖，1～4號四個虛線圓分別表示在不同時刻液滴內部壓力最大區域。圓面積的大小表示壓力最大區域的大小。如前所述，隨著驅動時間的延長，液滴內部壓力最大區域會依次從1～4四個位置進行不間斷的轉移，同時其面積也會不斷增大。當液滴內部壓力最大區域移動到4號圓所在區域時不會再繼續移動，而是保持在此位置并呈現出面積擴大的趨勢，此時液滴內部產生流體靜壓力差Δp，當Δp足夠大時就可以驅動液滴向壓力較小的方向運動。

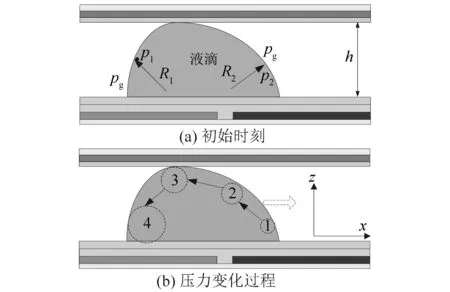
圖5 壓力最大區域變化示意圖(側視圖)Fig.5 Schematic diagram of maximum pressure area changes (side view)

根據文獻[19]中自由體表示法可以得到液滴在x方向所受“氣-液”表面張力分量大小：Fx=γlgcosθU，綜合以上分析，液滴在x方向所受介電驅動力、表面張力和流體靜壓力差近似相等，即其大小有如下關系：

Fx≈γlgcosθv≈Δp

(18)

在電場作用下,液滴從靜止到運動的過程中其內部的自由電荷和電偶極子與芯片厭水層中的表面束縛電荷相互吸引，此過程中出現的一個明顯變化是芯片的厭水層由厭水性變為親水性，隨著厭水層濕潤性增強，液滴的相應部分會攤開，攤開部分的接觸角減小，該攤開部分即為前進部分，這一過程中靜電力占主導作用，液滴所受力即為介電驅動力Fx；然后，液滴前進部分和恢復部分不同的表面形狀會使液滴產生形變，該形變會打破液滴原有的表面張力平衡狀態，此時液滴恢復部分的接觸角變化很小，可以忽略，表面張力占主導作用，液滴受到的表面張力大小為Fx。隨后，液滴恢復部分的流體靜壓力大于前進部分的流體靜壓力，不平衡的表面張力會破壞液滴內部的壓力平衡狀態，因此，液滴內部會產生流體靜壓力差Δp，當Δp足夠大時液滴就能夠被成功驅動。

為驗證液滴從靜止到運動的機理，本文設計制作了介電濕潤芯片。選用ITO玻璃作為芯片的基底，通過濕法刻蝕技術在ITO玻璃上制作出驅動電極。陣列驅動電極上驅動電極數為5，驅動電極尺寸為1 mm×1 mm，驅動電極間的間距為20 μm。選用SU-8光刻膠作為芯片的介電層，芯片介電層厚度為2 μm，其介電常數為3.2。使用雙面膠帶固定芯片上下極板，上下極板間距為300 μm，實驗過程中使用微量注射器把1 μL去離子水液滴置于芯片上。實驗室溫度為24 ℃，忽略液滴蒸發的影響，芯片具體制作工藝及實驗平臺搭建詳見文獻[10,22]。由于ITO玻璃具有較好的透光性，同時SU-8光刻膠烘干后變得透明，圖6a中用虛線表示的芯片中的驅動電極可見。圖6中，去離子水液滴前進部分位于導電驅動電極之上；液滴恢復部分位于非導電驅動電極之上，同時，該部分形狀保持原狀。這個過程中，液滴前進部分與恢復部分的表面強力非對稱的改變使得液滴產生一定程度的形變，此時，液滴非對稱的形變會在液滴內部產生流體靜壓力差。當液滴內部的流體靜壓力差足夠大時，液滴就能夠成功地由靜止狀態被驅動，當依次給陣列驅動電極施加一定量的驅動電壓時，液滴就能夠沿著陣列電極進行連續運動。

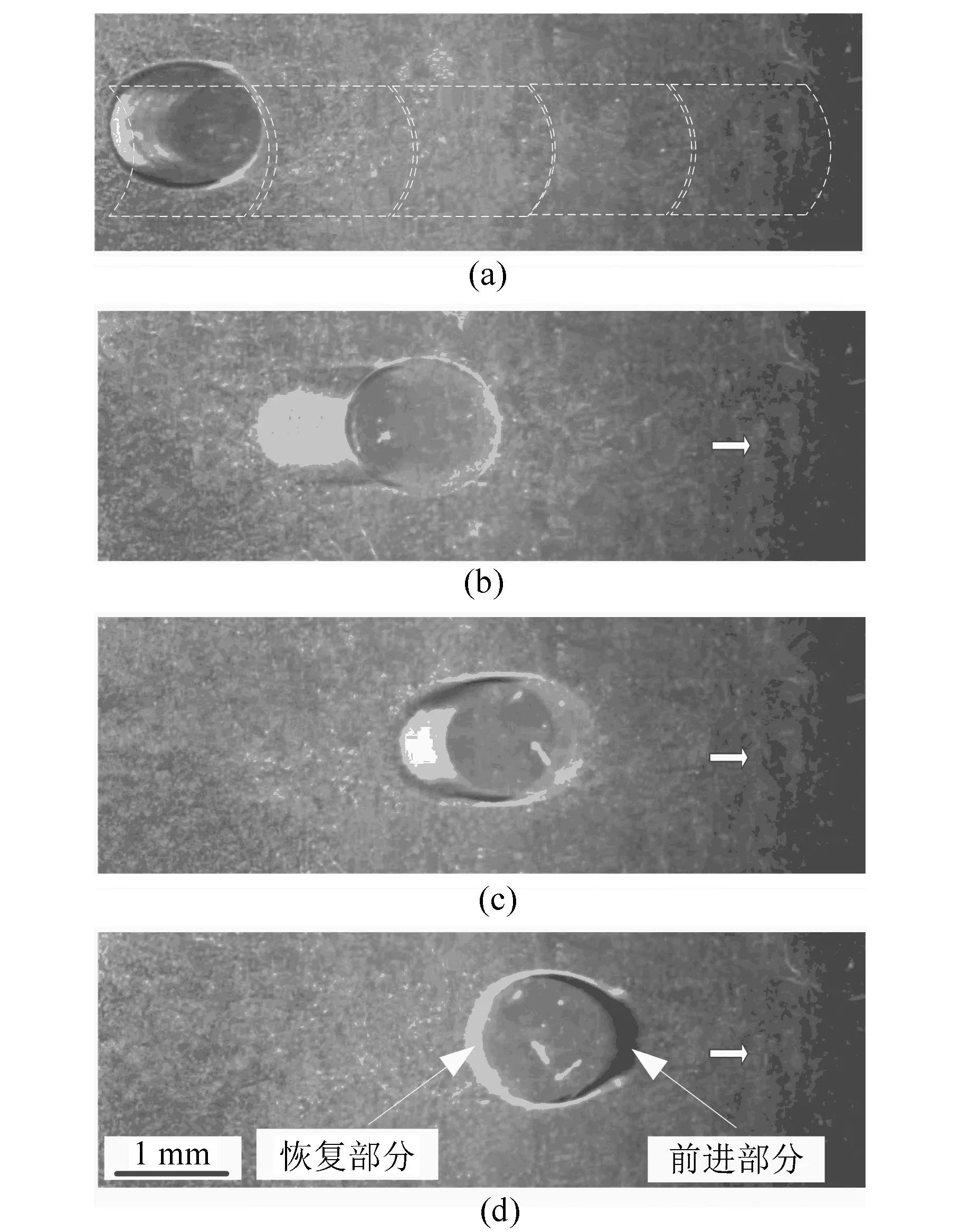
圖6 1 μL去離子水液滴運動視頻截圖(俯視圖)Fig.6 Video frame images of the 1 μL deionized droplet motion (top view)

綜上所述，介電濕潤芯片上液滴從靜止到運動需要依次經歷以下4個過程：

(1)把“EWOD芯片-液滴”看作是一個電容系統。當驅動電極導通時，位于導電驅動電極上方的液滴初始接觸角減小。

(2)接觸角減小會改變液滴的表面張力，而驅動電極不導通，則電極上方液滴的初始接觸角保持不變，其表面張力也保持不變。

(3)液滴前進部分與恢復部分的表面張力非對稱改變會使液滴發生一定量的形變。

(4)一定量的液滴形變會在液滴內部產生流體靜力壓力差，當流體靜力壓力差足夠大時就可成功驅動液滴。

4 結語

本文研究了介電濕潤芯片上固液接觸面表面束縛電荷作用機理；數值仿真了“EWOD芯片-液滴”系統中的電場，數值仿真結果和討論表明電場形成后在固液接觸面上的正負離子、分子相互吸引產生靜電力，該靜電力使液滴表面張力發生改變；而左右兩側非對稱的表面張力會使液滴產生形變，一定量的液滴形變會在其內部產生流體靜力壓力差，而足夠大的流體靜力壓力差會成功驅動液滴從靜止到運動；最后，通過1 μL去離子水液滴運動實驗對液滴從靜止到運動的過程和機理進行了驗證。為簡化模型和降低運算量，本文在進行數值仿真時忽略了液滴的蒸發及接觸角滯后與飽和效應對介電驅動力的影響。本文從本質上解釋了液滴從靜止到運動的過程，分析了液滴被成功驅動的機理，為更好地理解和利用數字微流控技術奠定了一定的理論基礎。