考慮終端姿態(tài)約束的自適應(yīng)迭代制導(dǎo)方法
郝釧釧 司 成 周曼娟
上海宇航系統(tǒng)工程研究所,上海 201109
隨著現(xiàn)代計(jì)算機(jī)技術(shù)和最優(yōu)控制理論的發(fā)展,也為了適應(yīng)空間發(fā)射任務(wù)多樣化、復(fù)雜化的現(xiàn)實(shí)需求,迭代制導(dǎo)方法在運(yùn)載火箭上得到越來越廣泛的應(yīng)用。美國(guó)的“土星”火箭和歐空局的“阿里安”火箭以及我國(guó)新一代運(yùn)載火箭均采用了迭代制導(dǎo)技術(shù)[1-3]。
迭代制導(dǎo)技術(shù)通過調(diào)整火箭飛行姿態(tài)控制其質(zhì)心運(yùn)動(dòng),為克服飛行過程中各種干擾的影響,會(huì)造成主動(dòng)段終端姿態(tài)散布較大,姿態(tài)偏差指標(biāo)設(shè)計(jì)值可能會(huì)超過20[2]。由于有效載荷對(duì)入軌姿態(tài)精度要求較高,對(duì)于沒有配備姿控發(fā)動(dòng)機(jī)系統(tǒng)的火箭,迭代制導(dǎo)會(huì)帶來較大的入軌姿態(tài)偏差;對(duì)于配備姿控發(fā)動(dòng)機(jī)系統(tǒng)的火箭,迭代制導(dǎo)引起的主動(dòng)段終端姿態(tài)偏差需要額外的星箭分離前姿態(tài)調(diào)整時(shí)間來克服,而這往往需要進(jìn)行飛行彈道調(diào)整以滿足本就比較緊張的“星箭分離后衛(wèi)星有效測(cè)控時(shí)間”需求,這也必然會(huì)導(dǎo)致一定的運(yùn)載能力損失。
為了同時(shí)滿足軌道參數(shù)約束和終端姿態(tài)約束,文獻(xiàn)[4]提出一種在線軌跡預(yù)測(cè)制導(dǎo)方法,以不考慮終端姿態(tài)約束的迭代制導(dǎo)姿態(tài)最優(yōu)解為初值,根據(jù)數(shù)值積分預(yù)測(cè)的火箭運(yùn)動(dòng)軌跡對(duì)最優(yōu)姿態(tài)進(jìn)行反饋迭代優(yōu)化;但該方法的復(fù)雜度和計(jì)算量遠(yuǎn)大于經(jīng)典迭代制導(dǎo)方法。文獻(xiàn)[5]提出一種基于聯(lián)立框架的直接法在線軌跡規(guī)劃方法,利用有限元正交配置進(jìn)行低階逼近和聯(lián)立求解,能同時(shí)滿足入軌精度和終端大姿態(tài)約束,但方法亞秒級(jí)的求解時(shí)間限制了其應(yīng)用。
受文獻(xiàn)[6]提出的一種通過在線估計(jì)火箭實(shí)際入軌點(diǎn)的緯度幅角進(jìn)行制導(dǎo)目標(biāo)點(diǎn)調(diào)整以精確控制近地點(diǎn)幅角的改進(jìn)迭代制導(dǎo)方法的啟發(fā),同時(shí)借鑒嫦娥三號(hào)著陸器動(dòng)力下降段的制導(dǎo)控制方法[7],本文提出一種考慮終端姿態(tài)約束的自適應(yīng)迭代制導(dǎo)方法,在確保有效載荷精確入軌的同時(shí)滿足主動(dòng)段終端姿態(tài)約束。并通過某型三級(jí)火箭的仿真分析證明了方法的有效性。
1 迭代制導(dǎo)的基本原理
迭代制導(dǎo)算法以終端坐標(biāo)系OE-XTYTZT為基本參考系,以地心OE為原點(diǎn),OEYT軸指向預(yù)估實(shí)際關(guān)機(jī)點(diǎn),OEZT軸垂直于軌道面并指向軌道動(dòng)量矩方向,OEXT軸與OEYT軸和OEZT軸構(gòu)成右手坐標(biāo)系。
在真空段忽略滾動(dòng)角時(shí)運(yùn)載火箭的運(yùn)動(dòng)方程如式(1)所示
(1)
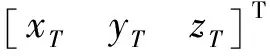
迭代制導(dǎo)方法以運(yùn)載火箭瞬時(shí)狀態(tài)為初值,以終端目標(biāo)狀態(tài)為終端約束,以火箭的一組姿態(tài)角為控制變量,以最短飛行時(shí)間為性能指標(biāo),構(gòu)造漢密爾頓兩點(diǎn)邊值優(yōu)化問題。在發(fā)動(dòng)機(jī)推力平穩(wěn)、地球引力場(chǎng)采用平均引力場(chǎng)近似等條件下,文獻(xiàn)[8]給出了該最優(yōu)控制問題的最優(yōu)姿態(tài)如式(2)所示
(2)
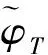
2 目標(biāo)點(diǎn)自適應(yīng)迭代制導(dǎo)方法
為了解決迭代制導(dǎo)引起的主動(dòng)段終端姿態(tài)散布較大的問題,本文將火箭末級(jí)主動(dòng)段按先后順序分為迭代制導(dǎo)段和姿態(tài)快速調(diào)整段;在末級(jí)主動(dòng)段結(jié)束前停止迭代制導(dǎo)進(jìn)入姿態(tài)快速調(diào)整段,利用主發(fā)動(dòng)機(jī)將火箭姿態(tài)調(diào)整至期望終端姿態(tài);在迭代制導(dǎo)段的制導(dǎo)計(jì)算中,根據(jù)對(duì)姿態(tài)快速調(diào)整段影響的實(shí)時(shí)估計(jì),自適應(yīng)確定迭代制導(dǎo)段終端的目標(biāo)狀態(tài)。
2.1 迭代制導(dǎo)段終端目標(biāo)狀態(tài)自適應(yīng)確定
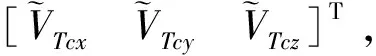
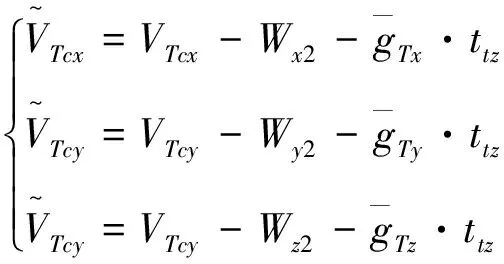
(3)
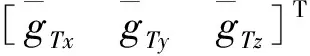
2.2 迭代制導(dǎo)段終端姿態(tài)估計(jì)
迭代制導(dǎo)段的終端目標(biāo)狀態(tài)確定后,可以按照文獻(xiàn)[8]中給出的經(jīng)典迭代制導(dǎo)算法進(jìn)行制導(dǎo)計(jì)算,計(jì)算迭代制導(dǎo)段的剩余飛行時(shí)間tk和如式(2)所示的解析形式的最優(yōu)姿態(tài)角。
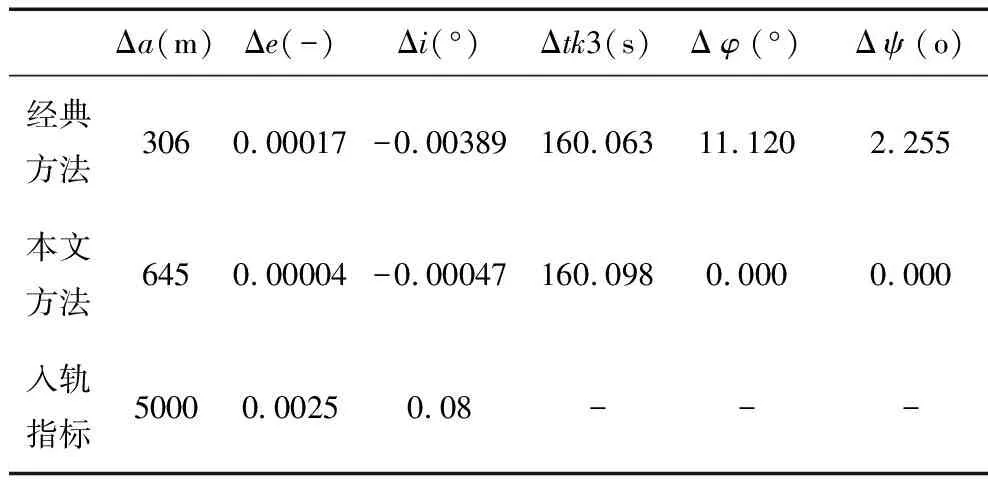
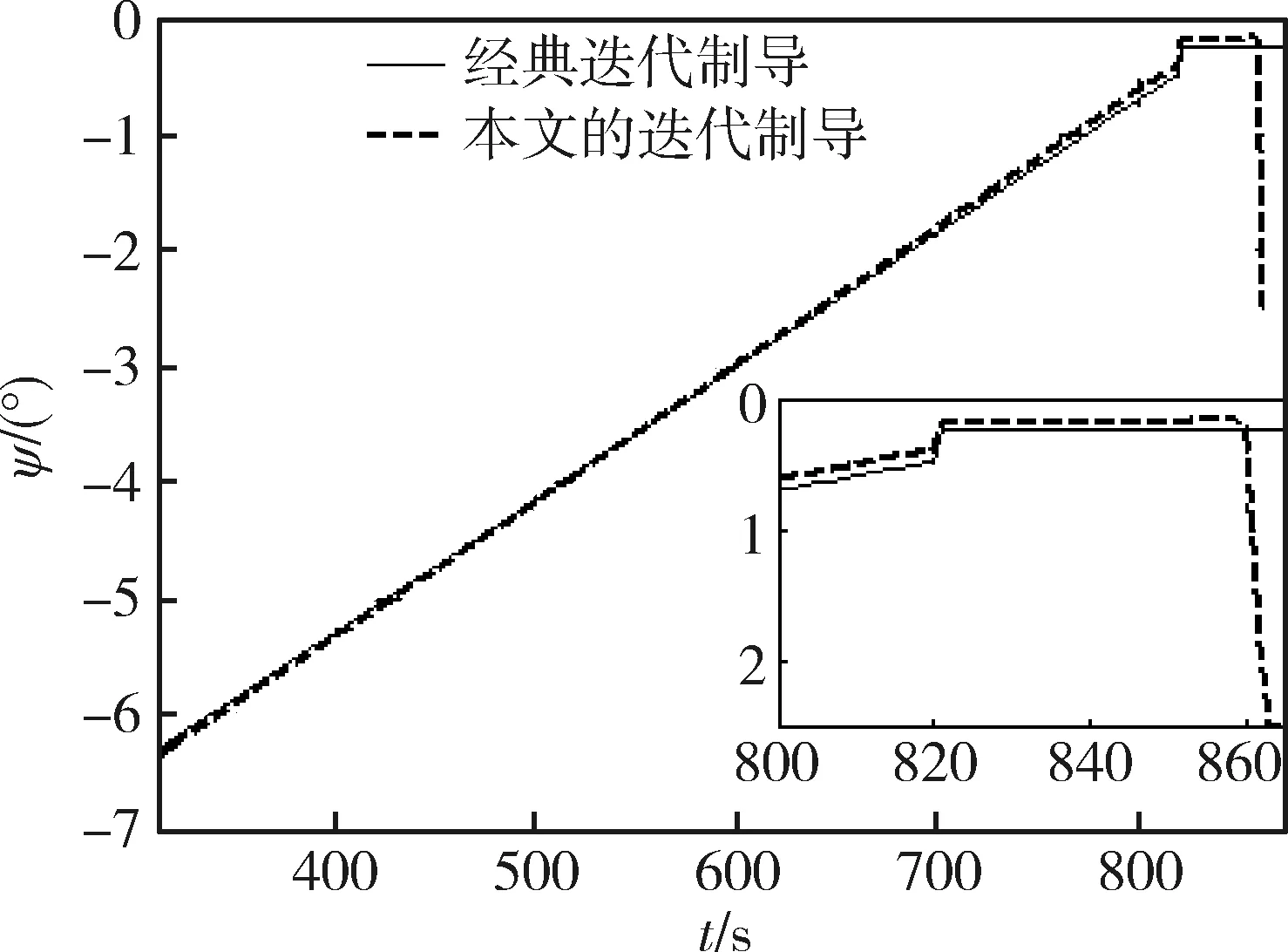
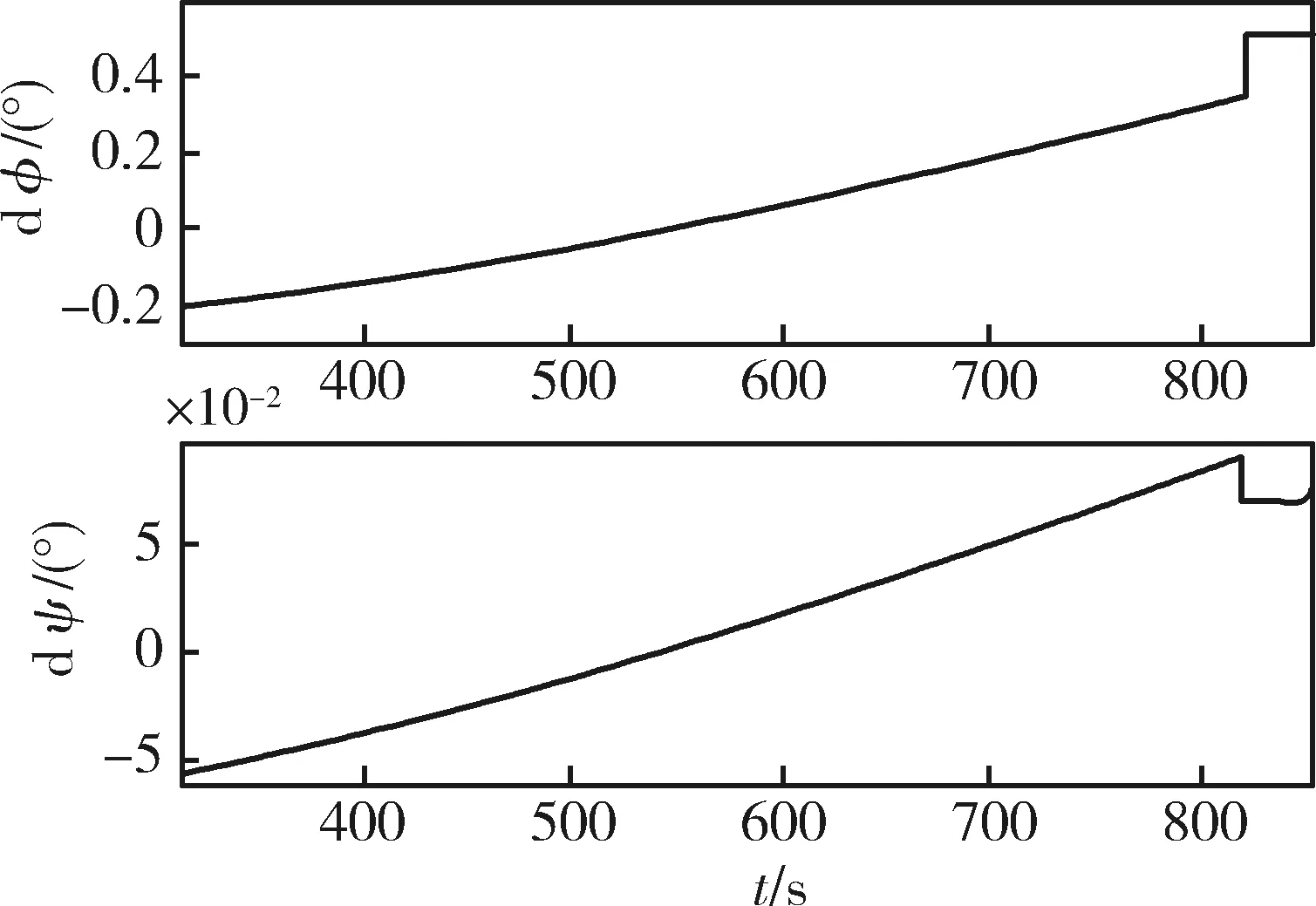
在工程實(shí)施上迭代制導(dǎo)往往采用分級(jí)制導(dǎo)方案,當(dāng)剩余飛行時(shí)間小于某一數(shù)值tzp時(shí),取消終端目標(biāo)位置約束;當(dāng)剩余飛行時(shí)間小于某一數(shù)值tzv(0 當(dāng)tk>tzp時(shí), (4) 運(yùn)載火箭制導(dǎo)控制的基本坐標(biāo)系為發(fā)射慣性系,它在火箭起飛瞬時(shí)與發(fā)射系重合。發(fā)射系以發(fā)射點(diǎn)為原點(diǎn),OXa軸在當(dāng)?shù)厮矫鎯?nèi)并指向發(fā)射方向,OYa軸沿發(fā)射點(diǎn)重力反方向,OZa軸與OXa軸和OYa軸構(gòu)成右手坐標(biāo)系。 (5) 其中,β為如圖1所示的預(yù)估主動(dòng)段終端與理論主動(dòng)段終端之間的地心角。 圖1 預(yù)估主動(dòng)段終端與理論主動(dòng)段終端間的地心角示意圖 參考經(jīng)典迭代制導(dǎo)中β的計(jì)算方法[8],考慮本文算法中到主動(dòng)段終端的剩余飛行時(shí)間(包括迭代制導(dǎo)段的剩余飛行時(shí)間tk和姿態(tài)快速調(diào)整段的飛行時(shí)間ttz),因此本文算法中β的計(jì)算方法如式(6)所示。 (6) 考慮到迭代制導(dǎo)段預(yù)估的剩余飛行時(shí)間是在對(duì)火箭運(yùn)動(dòng)方程作了簡(jiǎn)化處理后的計(jì)算結(jié)果,并且姿態(tài)快速調(diào)整段的開環(huán)飛行過程中會(huì)受到各種干擾的影響,為了確保實(shí)際飛行中主動(dòng)段終端的姿態(tài)調(diào)整到并穩(wěn)定在期望姿態(tài),將姿態(tài)快速調(diào)整段的姿態(tài)變化規(guī)律設(shè)計(jì)成如式(7)所示。 (7) 其中,t*為相對(duì)姿態(tài)快速調(diào)整段開始時(shí)刻的時(shí)間,ttz1(ttz1 由于液體火箭發(fā)動(dòng)機(jī)推力相對(duì)穩(wěn)定、火箭質(zhì)量變化緩慢連續(xù),因此推力視加速度變化緩慢連續(xù)。考慮到姿態(tài)快速調(diào)整段的時(shí)間比較短,因此可以近似認(rèn)為“整個(gè)姿態(tài)快速調(diào)整段的推力視加速度為固定值,數(shù)值上等于姿態(tài)快速調(diào)整段中間時(shí)刻的推力視加速度值”,見式(8) (8) 結(jié)合姿態(tài)快速調(diào)整段的姿態(tài)調(diào)整規(guī)律設(shè)計(jì),姿態(tài)快速調(diào)整段的推力視速度增量計(jì)算如式(9)所示。 (9) 姿態(tài)快速調(diào)整段的推力視位置增量的精確計(jì)算公式比較復(fù)雜。考慮到位置動(dòng)態(tài)相對(duì)于速度動(dòng)態(tài)為慢動(dòng)態(tài),以及軌道參數(shù)對(duì)位置偏差的敏感度較低。因此姿態(tài)快速調(diào)整段的推力視位置增量可以用式(10)進(jìn)行簡(jiǎn)化計(jì)算而不會(huì)對(duì)最終入軌精度產(chǎn)生太大影響。 (10) 由于迭代制導(dǎo)段的終端姿態(tài)估計(jì)會(huì)影響迭代制導(dǎo)段終端目標(biāo)狀態(tài)的確定,而迭代制導(dǎo)段終端目標(biāo)狀態(tài)又會(huì)影響迭代制導(dǎo)段的終端姿態(tài)估計(jì),因此需要對(duì)迭代制導(dǎo)段的終端姿態(tài)估計(jì)值進(jìn)行迭代計(jì)算。選擇主動(dòng)段終端的期望姿態(tài)作為其實(shí)際終端姿態(tài)的初始估計(jì),考慮終端姿態(tài)約束的自適應(yīng)迭代制導(dǎo)算法的計(jì)算流程為: 1)初始化:設(shè)置β=0,φTy(k)=φGs+90°,ψTy(k)=ψGs; 2)計(jì)算終端坐標(biāo)系下的期望終端姿態(tài):φTs=φGs+(90-β),ψTs=ψGs; 4)自適應(yīng)確定迭代制導(dǎo)段終端目標(biāo)狀態(tài); 5)用經(jīng)典迭代制導(dǎo)計(jì)算迭代制導(dǎo)段的剩余飛行時(shí)間tk及實(shí)際終端姿態(tài)角φTy(k+1)和ψTy(k+1)估計(jì)值; 6)若迭代制導(dǎo)段的終端姿態(tài)估計(jì)值收斂:|φTy(k+1)-φTy(k)|≤ε,且|ψTy(k+1)-ψTy(k)|≤ε,則迭代結(jié)束;否則,返回步驟2)。 以某型三級(jí)液體運(yùn)載火箭為例,對(duì)經(jīng)典迭代制導(dǎo)算法和本文提出的考慮終端姿態(tài)約束的自適應(yīng)迭代制導(dǎo)算法的制導(dǎo)控制效果進(jìn)行仿真分析。二級(jí)飛行段均采用經(jīng)典迭代制導(dǎo)算法,三級(jí)飛行段分別使用經(jīng)典迭代制導(dǎo)算法和本文的迭代制導(dǎo)算法。選擇三級(jí)關(guān)機(jī)點(diǎn)的期望終端姿態(tài)為:俯仰角為-41.267°,偏航角為-2.5°。 由經(jīng)驗(yàn)和仿真結(jié)果可知,三級(jí)發(fā)動(dòng)機(jī)秒耗量偏差對(duì)主動(dòng)段終端姿態(tài)影響最大。在三級(jí)發(fā)動(dòng)機(jī)秒耗量下降30%的情況下,2種迭代制導(dǎo)方案的仿真結(jié)果如表1所示。 表1 兩種迭代制導(dǎo)方案在“三級(jí)秒耗量下降30%”時(shí)的結(jié)果 由表1可知,與經(jīng)典迭代制導(dǎo)方案相比: 1)從入軌精度上看,采用本文的迭代制導(dǎo)方案時(shí),半長(zhǎng)軸偏差略大,但偏心率偏差和傾角偏差略小; 2)從三級(jí)發(fā)動(dòng)機(jī)關(guān)機(jī)點(diǎn)的姿態(tài)偏差上看,采用本文的迭代制導(dǎo)方案時(shí)的姿態(tài)偏差為0°,而采用經(jīng)典迭代制導(dǎo)方案時(shí)的俯仰角偏差達(dá)到11.120°,偏航角偏差為2.255°; 3)從三級(jí)關(guān)機(jī)時(shí)間偏差看,采用本文的迭代制導(dǎo)方案時(shí),三級(jí)飛行段多飛行35ms,多消耗推進(jìn)劑約1.2kg。 表明在“三級(jí)發(fā)動(dòng)機(jī)秒耗量下降30%”的情況下,本文的迭代制導(dǎo)方案在略微增加推進(jìn)劑消耗的情況下能很好地滿足終端姿態(tài)約束,并且入軌精度與常規(guī)迭代制導(dǎo)方案基本相當(dāng)。 2種迭代制導(dǎo)方案的三級(jí)飛行段俯仰、偏航姿態(tài)角對(duì)比分別如圖2和3所示。2種迭代制導(dǎo)方案的三級(jí)飛行段中的迭代制導(dǎo)段的姿態(tài)角偏差曲線如圖4所示。 圖2 兩種迭代制導(dǎo)方案的三級(jí)飛行段俯仰姿態(tài)角對(duì)比 圖3 兩種迭代制導(dǎo)方案的三級(jí)飛行段偏航姿態(tài)角對(duì)比 圖4 兩種迭代制導(dǎo)方案中迭代制導(dǎo)段的姿態(tài)角偏差 2種迭代制導(dǎo)方案的制導(dǎo)誤差綜合結(jié)果對(duì)比如表2所示。 由表2可知,采用本文的迭代制導(dǎo)方案時(shí)的入軌偏差與采用經(jīng)典迭代制導(dǎo)方案時(shí)基本一致,但三級(jí)關(guān)機(jī)點(diǎn)的姿態(tài)偏差為0°。采用經(jīng)典迭代制導(dǎo)方案時(shí),三級(jí)關(guān)機(jī)點(diǎn)的俯仰姿態(tài)偏差達(dá)7.344°、偏航姿態(tài)偏差為1.432°。 提出一種考慮終端姿態(tài)約束的自適應(yīng)迭代制導(dǎo)方法。將末級(jí)主動(dòng)段分為迭代制導(dǎo)段和姿態(tài)快速調(diào)整段。通過在線估計(jì)姿態(tài)快速調(diào)整段的影響,自適應(yīng)確定迭代制導(dǎo)段的終端目標(biāo)狀態(tài);并在姿態(tài)快速調(diào)整段將姿態(tài)調(diào)整至期望值。該方法能同時(shí)滿足軌道參數(shù)和終端姿態(tài)約束,僅增加少量推進(jìn)劑消耗,有很強(qiáng)的工程實(shí)用價(jià)值。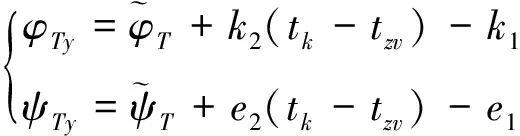
2.3 終端坐標(biāo)系下的期望終端姿態(tài)角計(jì)算
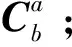
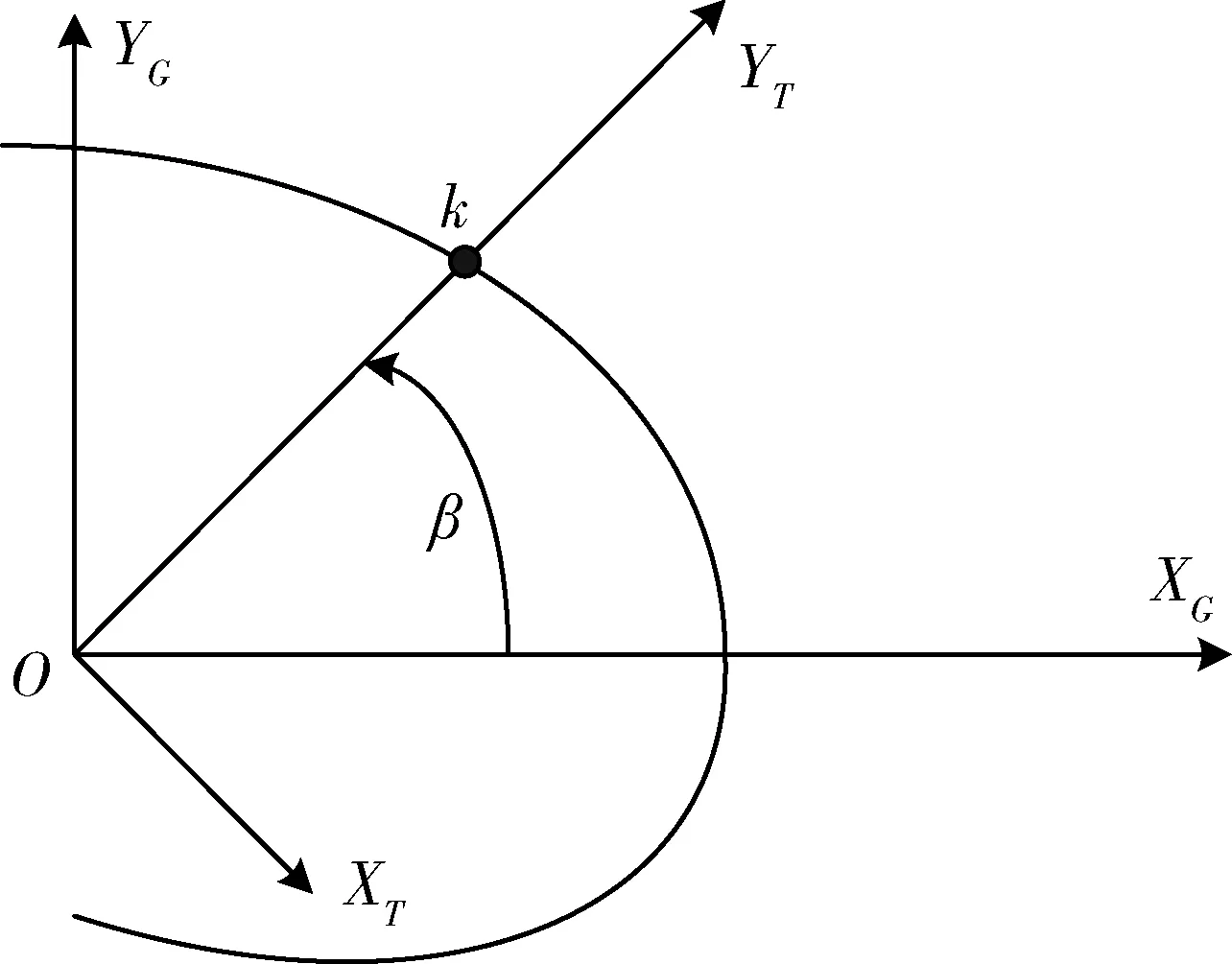

2.4 姿態(tài)快速調(diào)整段的姿態(tài)調(diào)整規(guī)律設(shè)計(jì)
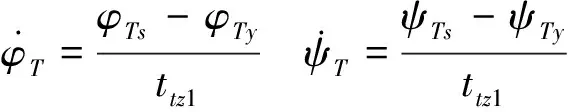
2.5 姿態(tài)快速調(diào)整段推力視加速度影響估計(jì)

2.6 自適應(yīng)迭代制導(dǎo)算法的計(jì)算流程
3 仿真分析

4 結(jié)論

